等边折线的离散曲率表示及应用

刘 婕， 张芳娟

(西安邮电大学 理学院， 陕西 西安 710121)

数学上的平面曲线由无穷多个点组成。在计算机图形学中，由于受内存资源所限，利用图形系统根本无法绘制出真正数学意义上的平面曲线，而是采用有限个离散点对其实现近似表示。采用离散点位置坐标显式地表示平面曲线，有利于图形系统快速高效地对其进行绘制，但这种表示无法反映平面曲线内在的几何特征。

平面曲线有一个内在几何特征，那就是曲率。曲线微分几何的基本定理表明[1]，在不考虑刚体运动变换的情形下，一条弧长参数平面曲线C(s)完全可由其曲率κ(s)描述。也就是说，两条平面曲线具有相同的曲率κ(s)当且仅当其中任意一条曲线是另一条曲线的刚体运动变换。若用积分形式描述，即是

(1)

其中

Circ(x)=(cosx, sinx)，

φ0是C(s)在s=0处的切线与x轴的夹角。可以看出，φ0和C(0)确定了刚体运动变换，一旦这两个参数以及曲率κ(s)给定了，则平面曲线C(s)就可通过方程(1)完全确定下来[2]。

考虑到实际平面曲线需要简化为离散形式，即平面折线或平面多边形，才可以方便处理，本文引入一种离散曲率的定义方式[3]，并由此得出，若不考虑刚体运动变换，给定内部顶点处的离散曲率和折线边长，即可完全确定一个平面等边多边形。此即曲线微分几何基本定理在平面等边多边形情形下的一种离散形式。

可以证明，只要给定初始顶点和初始边的方向，即可由离散曲率和边长值唯一确定一条平面等边折线，此外，其顶点坐标的解析表达式也容易获得。平面等边折线的这种离散曲率表示，可用于计算机动画中的变形(Morphing)。

变形是指从初始物体到目标物体的连续光滑自然的变换，这里的物体可以是图像[4-6]、曲线[2,7-8]、折线和多边形[9-12]、网格[13-15]等。变形必须解决“对应问题”和“插值问题”，即寻找初始和目标物体的对应关系，并实现两者之间自然光滑地过渡。本文将基于平面等边折线的离散曲率表示研究平面等边折线的变形插值问题。

1 平面等边折线的离散曲率表示

折线的离散曲率对应于曲线的曲率。若不考虑刚体运动变换，则给定离散曲率和边长，即可完全确定一条平面等边折线。

1.1 离散曲率的计算

平面曲线的离散曲率有多种计算方法[3, 16-19]。

平面折线P=[P0P1…Pn]任一顶点Pi处的离散曲率Ci由该顶点及其相邻两顶点Pi-1和Pi+1决定，即[3]

(2)

其中

整理即得

(3)

其中

L=[(xi+1-xi-1)2+(yi+1-yi-1)2]3/2。

公式(3)仅涉及到两点的距离以及由三个顶点Pi-1、Pi和Pi+1所确定的三角形的有向面积，由此定义的离散曲率跟平面曲线的曲率具有类似性质，即该定义的离散曲率具有平移旋转不变性，可以反映折线在顶点Pi处的弯曲方向。

1.2 由离散曲率和边长重构等边折线

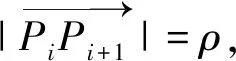
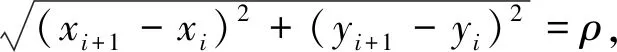
(4)

并通过逐个迭代，求得折线的各顶点。

1.3 平面等边折线重构的唯一性

重构出的平面等边折线是唯一的，即在不考虑刚体运动变换的情形下，方程组(4)的解是唯一的。

因折线是等边长的，故可通过简化离散曲率计算公式(3)，得出简化后的等边折线重构算法，即

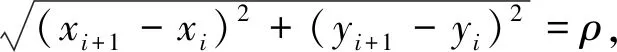
(5)

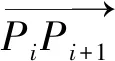
(6)

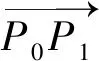
1.4 平面等边折线的顶点坐标表达式

由公式(6)和f(θi)=Ci≠0,可以得到

(7)

代入

得到方程组(5)的唯一解(xi+1,yi+1)。

若Ci=0,这意味着Pi+1与Pi,Pi-1共线，此时

因此，给定离散曲率C，边长值ρ，初始顶点P0(x0,y0)和初始边与x轴夹角θ0,重构出的平面等边折线的顶点表达式为

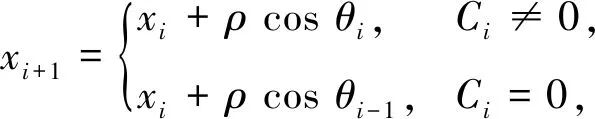
(8)

其中θi由式(7)给出。

2 离散曲率表示在变形中的应用

借助公式(1)重构中间时刻的曲线[2]，将其应用于变形所产生的过程自然光滑，但该方法计算复杂度较高，这是因为公式(1)一般无解析解，需要设计数值算法近似求解。以下尝试借助公式(8),利用离散曲率重构变形中间时刻的曲线。

2.1 方法描述

给定两条平面等边折线，分别记为

S0=[P00P01…P0n],
ST=[PT0PT1…PTn],

记时刻t的中间折线为

St=[Pt0Pt1…Ptn](0≤t≤T),

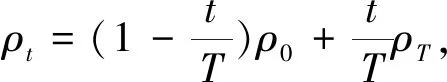
(9)

同样采用线性插值,得出折线St首个顶点Pt0及其首条边与x坐标轴的夹角θt0，即

(10)

2.2 实验结果

以“U”到“S”的变形为例,验证所给方法的有效性，并与文献[2,9]等方法所得结果进行比较。实验结果如图1所示。

图1 “U”到“S”的变形过程

由实验结果可见，所给方法与文献[2，9]方法的变形结果很接近，变形过程自然光滑。从计算复杂性角度来看，所给方法比文献[9]方法复杂度略高，但比文献[2]方法简单许多。当然，在4种方法中，线性插值方法的复杂度最低，但在变形过程中出现扭曲和自交现象。

3 结语

给出曲线微分几何有关曲率基本定理的一种离散形式，即平面等边折线的离散曲率表示。证明了当给定内顶点处的离散曲率和折线的边长值时，只要再给定初始顶点和初始边的方向就可以唯一确定一条平面等边折线。同时给出了顶点的解析表达式，并将离散曲率表示用于平面等边折线的变形。