基于ACO-SVM的岩质高边坡锚杆轴力预测

2019-05-05孟子耀陈志坚

中国煤炭地质 2019年3期

孟子耀，陈志坚，陈涛

(河海大学地球科学与工程学院，南京 211100)

0 前言

人工锚固岩质高边坡的稳定性问题一直是岩土工程研究的一个重要领域[1]。边坡内部的位移与应力监测是评价边坡稳定性的重要手段。目前较多学者在边坡位移监测上提出了新的理论与方法。杨皓翔[2]等建立基于拉格朗日插值法的新陈代谢模型，在边坡的位移监测应用中取得了较好的效果；孙健[3]提出将光纤光栅位移传感器布设在潜在滑动面上的方法，得到了动态的位移监测曲线；徐茂林等[4]通过引入TM30测量机器人，实现了位移监测数据的高度自动化采集；周丽静等[5]基于北斗卫星系统的定位及通信功能构建了露天矿边坡位移监测系统；Osasan等[6]基于逆速度法建立边坡破坏时间预测模型，取得了较好的效果; I.B.Kwon等[7]利用OTDR测量光纤信号并通过光纤信号的差值对边坡的稳定性进行分析，证明了位移监测系统的可行性；Josep等[8]将GPS位移监测系统的结果与传统监测仪器结果进行对比，发现不受天气和通视条件影响的GPS监测系统在边坡位移监测中具有一定的优越性。

然而，位移监测仍然存在预警滞后的特点，通过监测和预测锚杆轴力的变化趋势，可以更及时地掌握边坡的安全状况，提前预警。本文通过构建ACO-SVM预测模型，结合连云港某人工锚固岩质高边坡的锚杆轴力监测数据，对模型可靠性及工程应用可行性展开讨论。

1 多因素ACO-SVM 预测模型的构建

1.1 支持向量机(SVM)

支持向量机是20世纪90年代由Vapnik等[9]提出来的一种神经网络模型，能输入多种影响因子并根据有限的样本信息在模型的复杂性和学习能力之间寻求最优解输出预测值。支持向量机可通过寻找满足分类要求的最优超平面来实现回归预测的功能[10]，设样本集为T=(xi,yi)，i=1,2，…，n；y= { 1，-1}是类别标号，其中i为样本个数，xi∈Rn，Rn为n维实数空间，超平面方程为：

ω·xi+b=0。

(1)

其中ω为超平面的法向量，b为超平面的偏移量。标准的支持向量机可通过如下的求解式来确定ω和b：

(2)

yi((ω·xi)+b)≥1-ξi，

ξi≥0，i=1,2,…,n。

(3)

式中ξi为松弛变量，C>0为惩罚因子。

温度、地下水位和时间作为影响锚杆轴力变化的三种因素，与锚杆轴力之间存在较为复杂的非线性关系。因此，本文通过 MatLab 编写可考虑多因素非线性变化规律的支持向量机模型(SVM)来对锚杆轴力进行预测分析。

首先确定目标函数为：

(4)

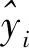
SVM程序的性能很大程度上要受到惩罚因子C和核函数类型及参数选择等因素的制约[11-12]。为提高模型的预测效率，本文引入蚁群算法(ACO)对支持向量机中的惩罚因子C和核函数中的参数γ搜索寻优。

1.2 蚁群算法(ACO)

蚁群算法是由Marco Dorigo基于生物学理论提出的一种寻找最优路径的机率型算法[13]。由于其具有全局搜索能力强和并行性的搜索方式等优点，广泛应用于人工智能、交通运输等领域[14-15]。

蚁群算法的关键在于移动规则和信息素更新，具体步骤如下：

步骤1.蚁群系统初始化。

步骤2.根据公式(5)选择下一步的路径。

(5)

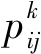
步骤3.释放信息素。

步骤4.经过一次循环后对路径上的信息素按公式(6)、(7)进行更新

τij(t+1)=ρ·τij(t)+Δτij(t,t+1)。

(6)

(7)

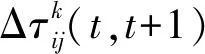
蚁群算法优化SVM 模型参数的主要思想是通过定义域内一组参数C和γ作为蚂蚁的位置向量，搜索出使式(4)最小的一组参数，具体流程如图1所示。

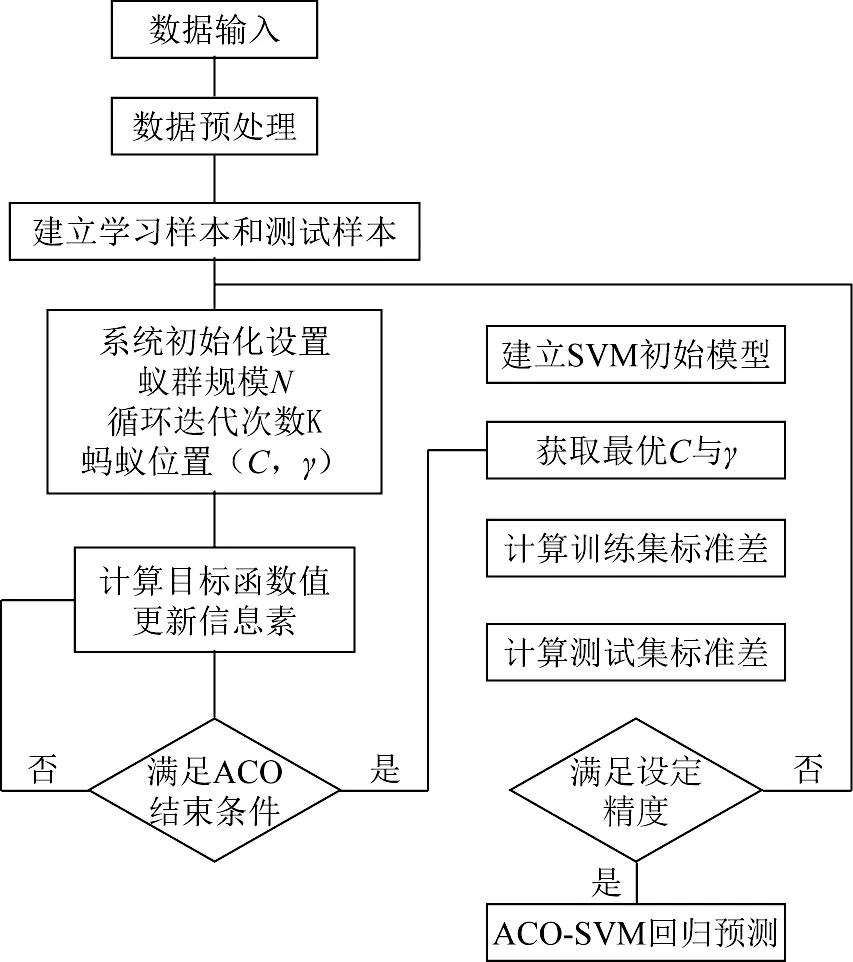
图1 ACO优化SVM流程Figure 1 ACO-SVM flow chart

2 工程应用

2.1 工程概况

连云港港东疏港高速公路位于连云港东北部市郊，起自老港区以东约500m处，路线向南相继以隧道形式穿过后云台山与后云台山炮台顶，在中云台山处改用明挖施工，因而形成了长度约1km的高陡人工路堑岩质边坡，最大坡高200多米，属一级边坡工程。

边坡区内无断裂，第四系覆土层很薄，基岩为一套前震旦系海州群云台组变粒岩、浅粒岩，岩性以灰白，肉色白云钠长变粒岩为主，其中二长浅粒岩为主，中部夹绿泥石片岩，下部夹钠长浅粒岩。其中绿泥石片岩抗压强度低，遇水易软化，且抗风化能力差。左侧边坡北侧存在废弃采石场，南侧采石场仍处于作业状态。右侧边坡在放坡过程中偶采用爆破施工。边坡区受季风影响，副热带高气压的进退时常酿成暴雨，同期还有台风活动，会带来大量的降水，春夏雨量占全年降水量的74%。

工程边坡岩体以块状结构为主，局部节理发育地段呈碎裂结构，偶尔在节理密集带也可见到碎裂—散体结构。边坡岩体构造结构面发育，且存在一定数量的顺倾、缓倾结构面，裂隙发育，富含裂隙水。当场区附近存在爆破、开挖或持续性降雨时均有可能发生边坡失稳和局部岩体塌方。为了解边坡内部应力场的变化规律和发展趋势，施工期在不同开挖高程总计陆续设置了70个锚杆轴力监测观测点，部分测点布置如图2所示。

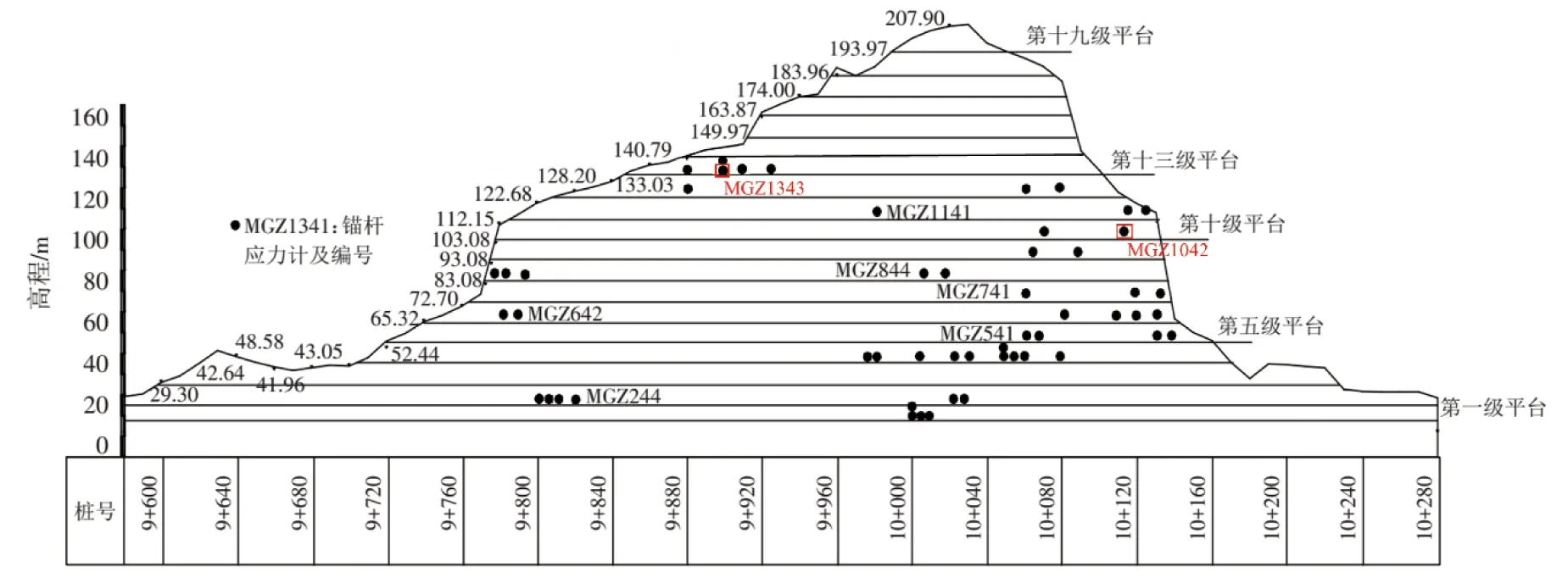
图2 测点布置Figure 2 Measuring points layout

2.2 预测模型的可靠性分析

本文选用左侧边坡第十三级平台处MGZ1343测点(桩号K9+900m)的锚杆轴力实测数据进行分析，选取2017年7月31日至2017年9月8日中每天0：00、6：00、12：00和18：00的数据共计160组进行研究。由于样本数据过大，仅展示部分监测数据如表1所示。

首先选取前150 组数据作为训练样本，训练完成后，通过ACO-SVM预测模型得到10组轴力数据，并将预测结果与实测值进行对比，分析该预测模型的可靠性。

MGZ1343轴力实测值与预测值的对比结果如表2，变化趋势对比如图3。

由表2可知，前三组数据预测轴力值要小于实测轴力值，对边坡的稳定性评价而言偏保守。从第四组数据开始，预测轴力值与实测轴力值的差值开始出现正负交替，且相对误差更小，更能反映实际的锚杆轴力变化情况。

通过轴力值的变化趋势图可以更加直观地发现，基于ACO-SVM的锚杆轴力预测模型所得出的预测值与实测值拟合度较高，预测轴力值在实测轴力曲线上下小范围内波动，经计算相对误差在8%以下，具有较高的可信度和预测精准度。

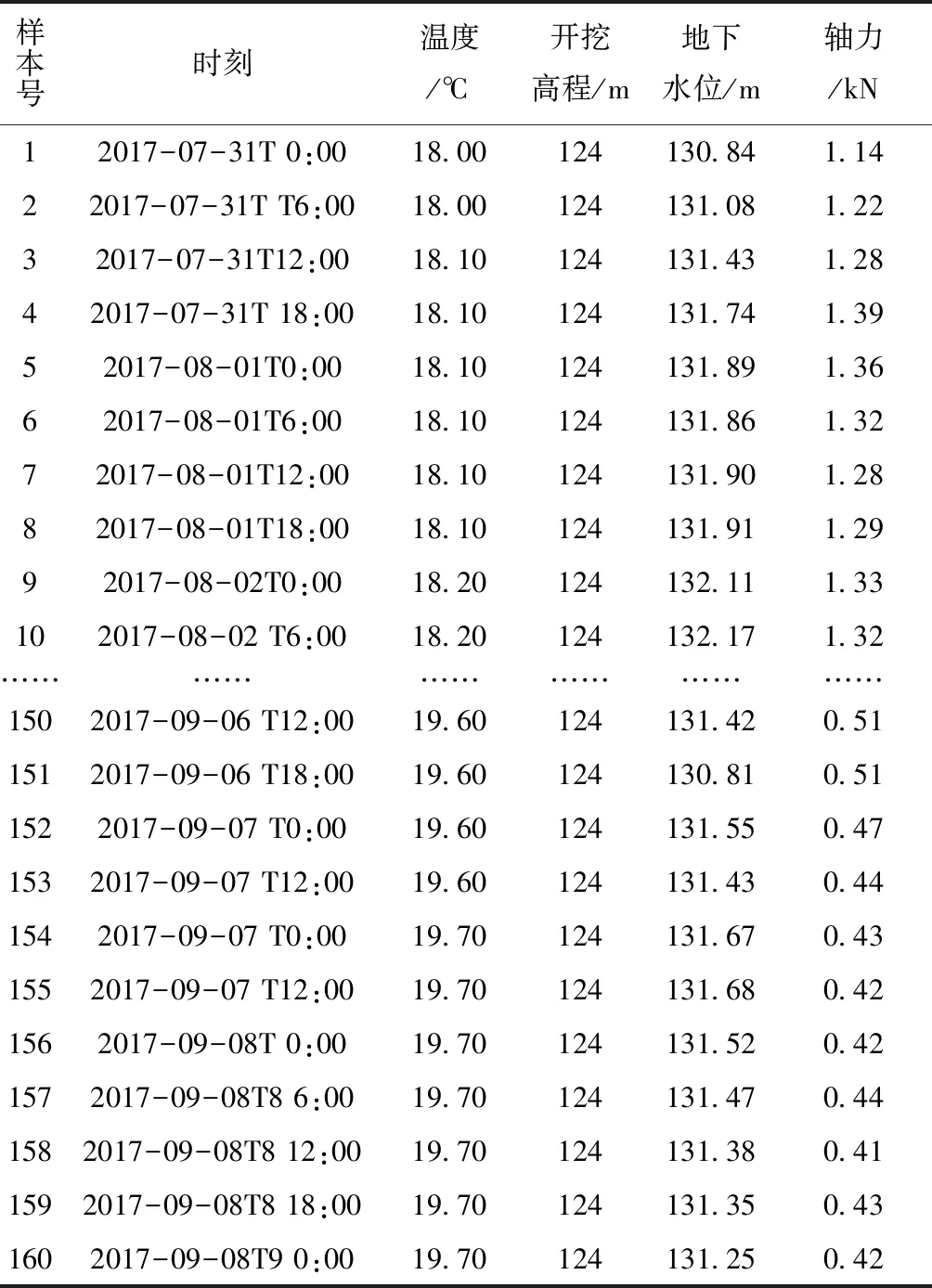
表1 MGZ1343测点锚杆实测数据

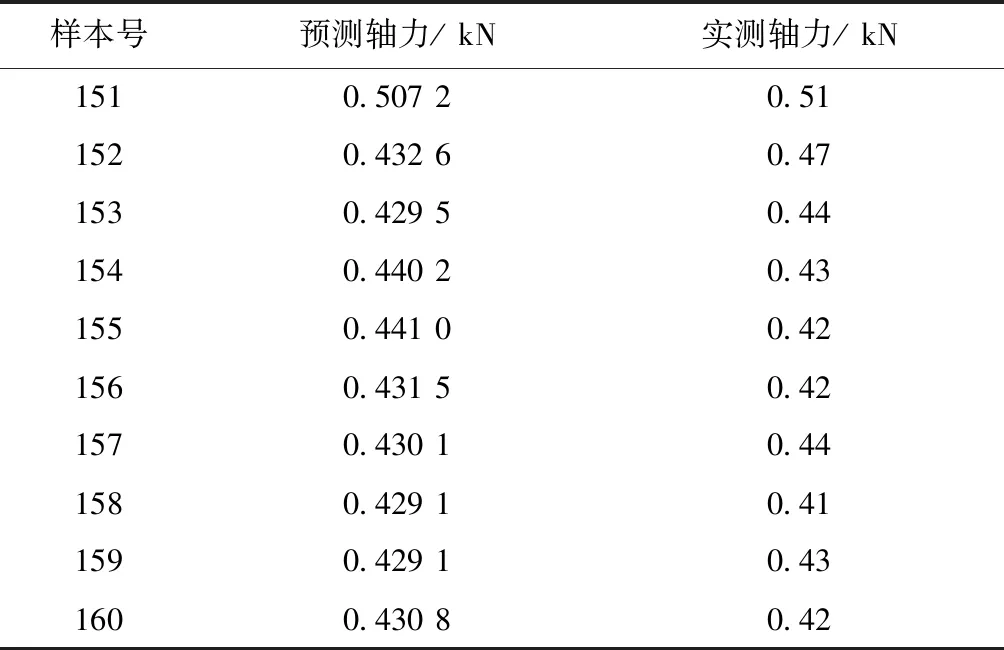
表2 锚杆轴力实测值与预测值对比

2.3 预测模型的可行性评价

ACO-SVM模型对锚杆轴力的预测功能得到验证后，可在每月月底将当月实测轴力数据作为训练样本来预测轴力的变化趋势。

在2018年4月底的锚杆轴力数据处理中，以左坡104平台处MG1042测点(桩号K10+117m)4月份实测轴力值为训练样本，依靠该预测模型得到5月上旬轴力变化曲线如图4所示。

由图4可知，4月份104平台锚杆轴力实测值在一定范围内上下波动，月末已有增大的趋势。通过ACO-SVM模型预测得到的5月上旬锚杆轴力值远高于4月份的平均水平，涨幅高达43%，已超过边坡稳定性预警的标准。

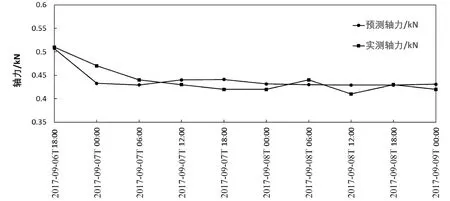
时刻图3 轴力实测值与预测值折线Figure 3 Line chart of axial force measured data and predicted data

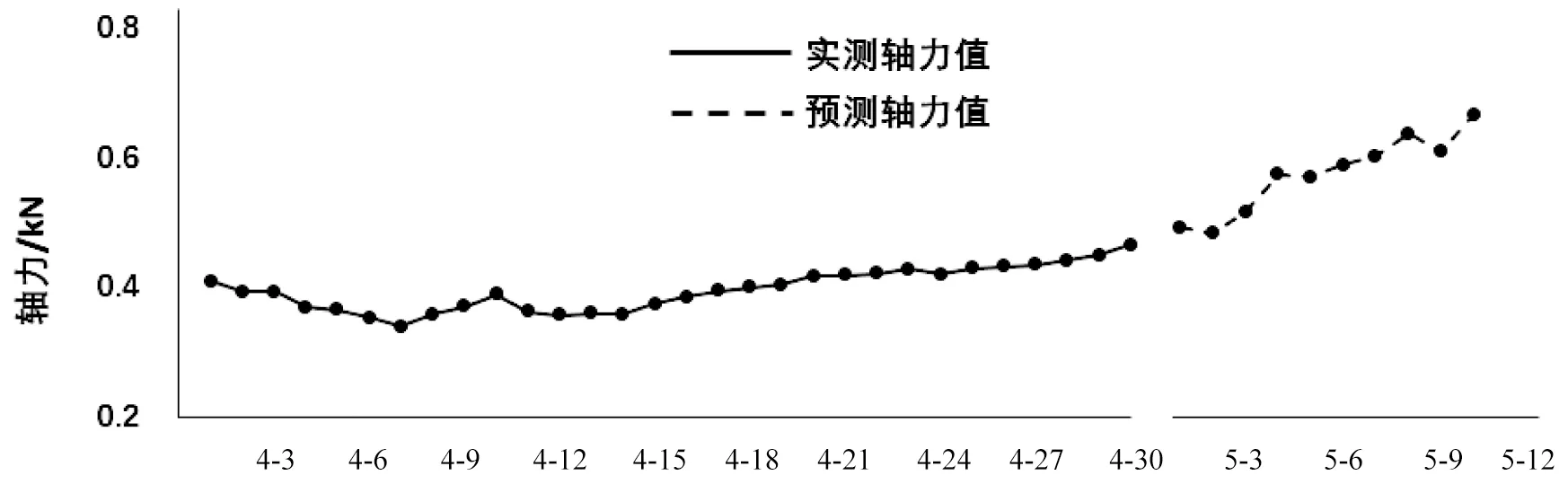
日期图4 104平台锚杆轴力变化趋势Figure 4 Anchor bolt axial force variation trend on No.104 platform

通过现场踏勘调查结果，左坡104平台南侧临近采石场处的确存在欠稳定三角体，但未见明显位移，如图5所示。锚杆轴力预测值增大的原因可能是4月份的连续降雨导致此处结构面强度降低，使该欠稳定三角体存在下滑趋势。为防止崩塌滑坡灾害对坡脚高速公路运营及行人行车安全造成损失，可在其发生滑动破坏前进行治理。

图5 欠稳定三角体Figure 5 Understable pyramid

在欠稳定三角体未发生明显位移阶段，单靠位移监测无法及时发现问题，而此时通过锚杆轴力预测的方法可提前探知该欠稳定三角体的发展情况。

在采集到MGZ1042测点5月份的锚杆轴力实测值后与ACO-SVM轴力预测模型的预测值进行对比，如图6所示。结果再次验证了该模型的可靠性，并且通过多次样本训练， ACO-SVM模型所得的预测结果与实测的数据之间相对误差更小，拟合程度更高。说明基于ACO-SVM的锚杆轴力预测模型在分析边坡稳定性时有一定的可行性。