GARCH模型控制图的构造与应用
2019-05-05刘晓华
刘晓华
(山东工商学院 统计学院,山东 烟台 264005)
0 引言
将统计过程控制应用于金融领域是最近二十年才开始的工作,从国内外研究成果可以看出,将统计过程控制用于金融风险管理的理论研究还不完善,需要对模型进行改进。本文在传统控制图的基础上,针对金融序列中出现的自相关和异方差性,用自回归模型AR提取相关性,用条件异方差模型GARCH提取异方差性,再对残差建立控制图,并利用沪深300指数进行了实证分析,结果表明残差控制图可以很好的监控金融风险。
1 控制图相关理论
1924年休哈特首先提出了控制图的理论,此后控制图的相关理论广泛应用于质量管理相关领域,并在实际应用过程中,根据各种可能的情况,出现了相应的修正控制图。控制图主要由三条标志线构成,最上面的是上控制限(UCL),最下面的是下控制限(LCL),中间的为中心线(CL),其中上限控制限的确定依据小概率事件原理。
以正态分布N(μ,σ2)为例,根据分布性质可知P(|X-μ|≥3σ)=0.0026,也就是说样本数据落在μ±3σ外的概率很小,在3‰以下,是一个小概率事件。由此确定控制限分别为:

在控制图中,如果过程运行正常,则点会落在上下控制限内。而如果点一旦落在上下控制限之外,则根据小概率事件原理,小概率事件一旦出现,则意味着系统出现异常,需要进行调整。
在通过控制图对质量过程进行监测的过程中,主要有两类错误:第一类错误是实际过程未发生异常,但是点落在了控制限外,根据控制图判定过程异常,犯了弃真的错误,犯第一类错误的概率一般用α表示。第二类错误是实际过程已经发生异常,但是点落在了控制限内,但是根据控制图判定为过程正常,犯了取伪的错误,犯第二类错误的概率用β表示。犯这两类错误的概率不同时最小,此消彼长。在控制图设计时,应尽量使得犯这两类错误造成的总损失最小。
常规控制图在设计过程中通常假定独立同分布,但实际的质量过程经常出现一定的自相关性,对此常用的改进方法主要有两种:
第一种方法是调整常规控制图的控制限,通过改进方差的估计来对控制限进行调整。
第二种方法是对残差建立控制图,首先对数据建立合适的时间序列模型提取序列中的自相关性,再构造残差序列,拟合后的残差值通常满足独立同分布,符合常规控制图的假定,由此构造残差控制图进行控制。
2 自回归模型AR的设计
自回归模型AR是用变量自身的滞后项为自变量进行回归,p阶自回归记为AR(p),其模型形式如下:
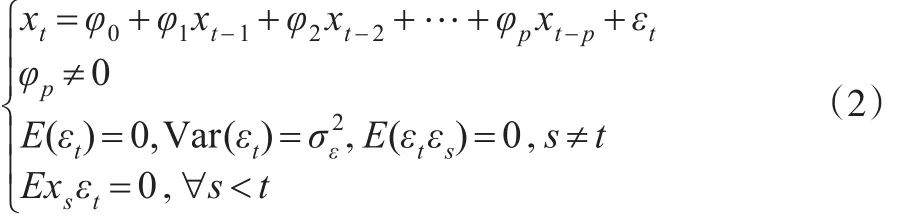
模型有三个限制条件,条件一:φp≠0保证了模型的最高阶是p;条件二:E(εt)=0,Var(εt)=σ2ε,E(εtεs)=0,s≠t则要求随机干扰序列是零均值的白噪声过程;条件三:Exsεt=0,∀s<t,则说明当前的随机干扰与过去的序列无关。
在AR(p)序列中,通常要求过程平稳,需要满足的条件为模型对应的特征方程对应的特征根都在单位圆内。
以AR(1)为例介绍AR模型残差控制图的构造。
3 条件异方差模型GARCH控制图的设计
在金融时间序列分析中,数据经常表现某一特征的值成群出现的情况,即波动的集群性。在进行分析时,数据同时表现为自相关和异方差,此时需要使用自回归条件异常差模型,即ARCH模型。ARCH(q)模型形式如下:
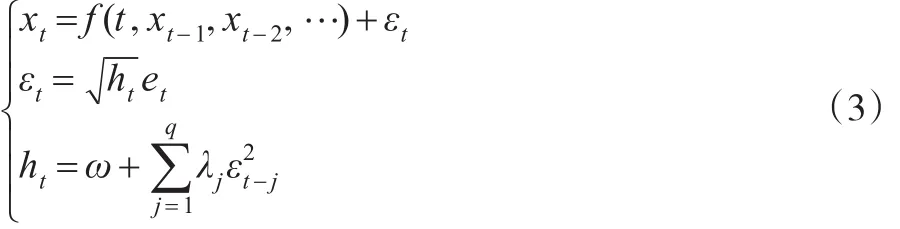
ARCH模型实际上使用残差平方序列的q阶移动平均拟合当期异方差,由于移动平均MA模型的自相关系数q阶之后截尾,所以ARCH模型只适用于具有短期相关性的异方差函数。但在实际中,残差序列的异方差函数可能具有长期相关,此时如果使用ARCH模型拟合异方差,将产生很高的移动平均阶数,造成参数估计的难度增加和模型的拟合精度受影响。
为了修正这个问题,Billerslov在1985年提出了广义自回归条件异方差模型(GARCH),模型GARCH(p,q)形式如下:
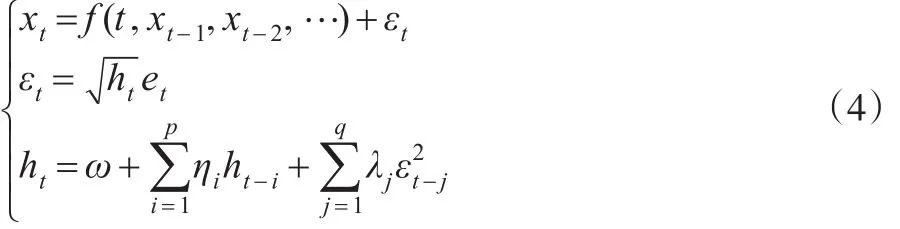
条件1:参数非负,即ω>0,ηi≥0,λj≥0。
假设{xt}同时存在自相关性和异方差性,其表达式为xt=mt+ηt=E(xt|xt-1,…)+ηt。其中,mt为在给定t时刻之前信息的条件下xt的条件均值,ηt为相互独立的扰动项,因为xt存在序列相关性,可以用AR模型进行拟合,此时,则残差序列为εt=xt。其中为参数的估计值为条件均值的估计值。
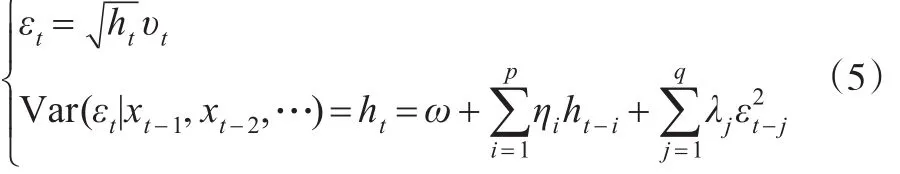
此时υt~N(0,1),则有εt~N(0,ht),又因为,则,则在置信水平在99.73%下,有,因此基于序列{}xt的控制图,其控制限为:

因为,ht随着时间t而不断改变,所有中心线和上下控制限都会波动,这三条控制限的变动会使得对异常值的判断带来困难,因此可以对残差进行控制。在中进行变形得到,也就是说,在时刻t,残差εt落在中的概率为99.73%,按照小概率事件原理,如果点落在在外,可以判断为异常点。这样对序列{xt}的监控可以转化为对残差序列{εt}的监控,即为残差控制图,其控制限为:

在残差控制图中,中心限为直线,只有上下控制限是变动的,相对于之前的控制限式(6)有了很大改善,在使用过程中也很方便。
4 实证分析
本文以沪深300综合指数进行实证分析,样本时间为2005年1月4日至2017年10月13日,除去节假日,共3104个样本数据,数据来源于同花顺软件。在对股指进行数据分析中,人们一般关心收益率的波动,首先将原始数据通过rt=ln(Pt)-ln(Pt-1)转换为对数收益率,其中rt为第t天的对数收益率,Pt为第t日的沪深300指数日收盘价。
对对数收益率rt的序列进行分析,时序图如下页图1所示。
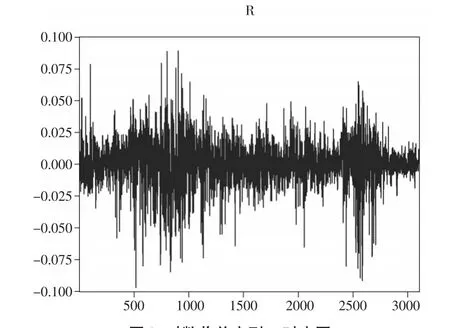
图1 对数收益序列rt时序图
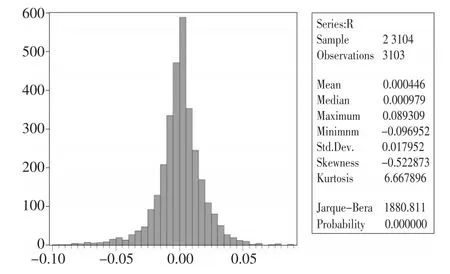
图2 对数收益率序列rt描述统计图
从图1中可以看出,数据表现出在一定的时间段内(如1500~2000)波动比较小,但是在有的时间段(500~1000和2300~2700)波动很大,存在明显的集聚效应。由图2的直方图和描述性统计分析可以看出:数据SK=-0.52<0,分布时左偏的,峰度系数KU=6.667,高于正态分布的峰度3,收益率序列是尖峰分布。因此收益率序列同时具有尖峰和厚尾的特征,这也是一般收益率序列的特征。
4.1 GARCH模型的建立
首先需要对数据进行平稳性检验,ADF检验的结果t统计值值为-54,小于0.01水平下的临界值-3.43,对应的p值为0.0001,拒绝存在单位根的原假设,数据平稳。接下来根据自相关图建立相关回归模型。
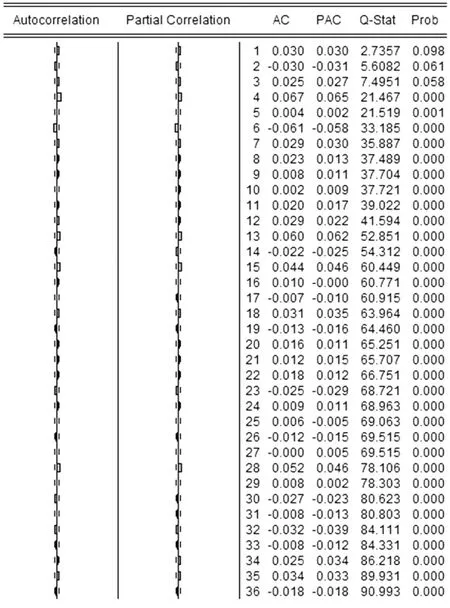
图3 对数收益率序列的自相关图
由图3序列的自相关图可以看出,序列存在明显的自相关,但是自相关的阶数不易确定,通过尝试,最终通过系数显著性检验的模型见表1。

表1 AR模型估计结果
由此确定的表达式为rt=0.0658rt-4-0.0586rt-6+εt。
接下来对残差进行分析,通过图4可以看出,残差波动具有明显的集群效应,进一步对残差进行ARCH-LM检验,F统计量为39.46,对应的p值为0,拒绝原假设“ARCH模型残差不存在异方差性”,说明收益率序列存在明显的异方差性,需要建立条件异方差模型。
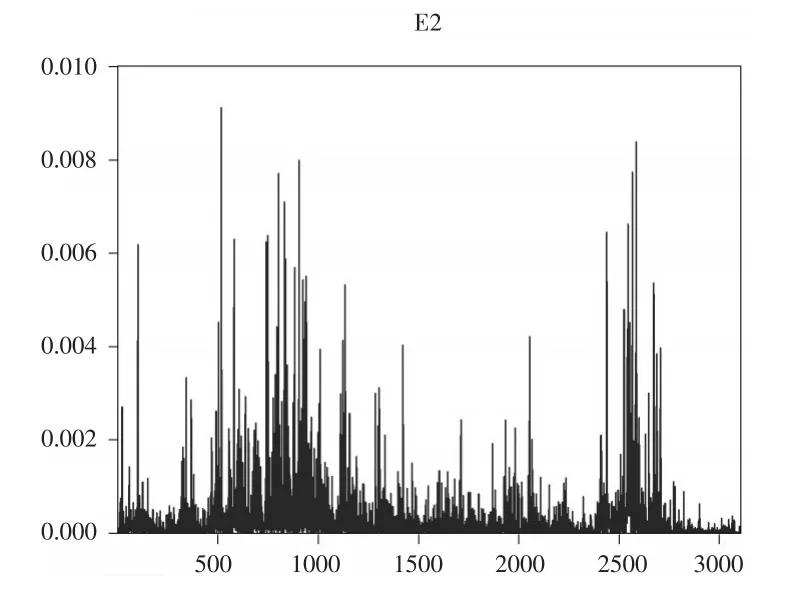
图4 残差平方自相关图
对残差建立GARCH(1,1),输出结果,AR(4)系数的显著性检验对应的p值为0.2325,未通过检验,剔除重新建立模型,参数估计的结果如表2所示。
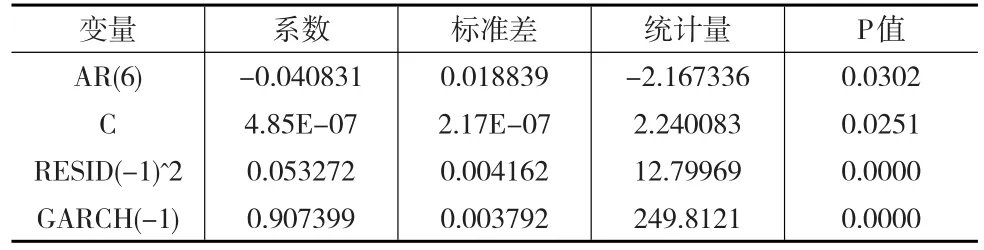
表2 GARCH模型估计结果
进一步构造GARCH(1,2)和GARCH(2,1),对信息量进行对比,GARCH(1,1)最优。故最终模型为:
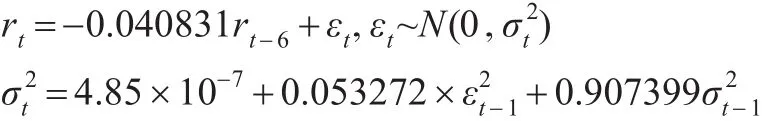
模型系数都大于0,且0.053272+0.907399<1,满足约束条件。
对残差再做ARCH-LM检验,对应的F统计量为1.0341,p值为0.3,序列不存在异方差,自相关检验的结果,序列不存在自相关性,即残差序列相互独立和等方差,满足控制图的假定。
4.2 残差控制图的建立
残差满足独立性和等方差性,符合控制图的要求,对残差按照式(7)构造控制图,如下页图5所示。
从图5看出,在500~1000(对应时间为2007—2008年)之间和2500~2700(对应时间为2015—2016年)之间的点出界的比较多,主要原因在于这两个时间段中国股市经历了大起大落,在控制图中这两个时间段超出控制限的点最多。假定定义|rt|≥0.05为异常点,在用残差GARCH控制图进行分析,判定的情况如表3所示。
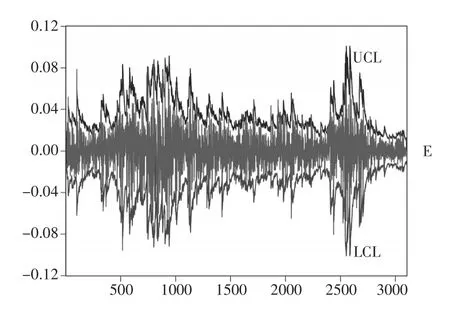
图5 GARCH控制图
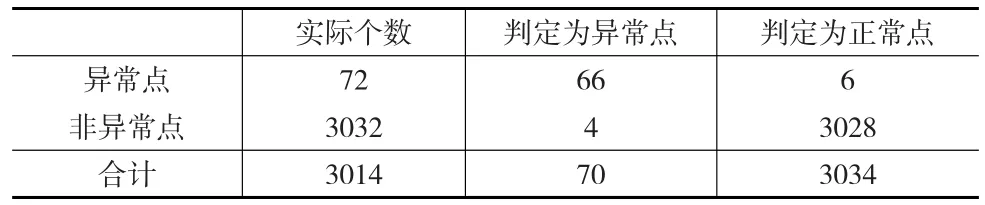
表3 GARCH控制图分析情况表
依据表3,可以计算得到犯一类错误的概率α为4/3032=0.0013,犯第二类错误的概率β为6/72=0.083,犯两类错误的概率都很小。
通过图5可以看到控制图能把很好监控出异常点,下面通过图6和图7这两个时间段对有代表性的日期进行分析。
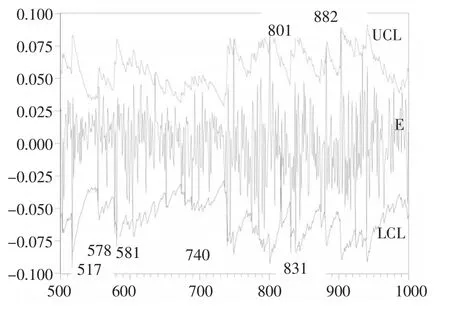
图6 500—1000号控制图
图6中第517号对应日期是2007年2月27日,收益率为-9.7%,超过了控制下限,主要诱因是全球股市暴跌引起A股连锁反应,当日跌幅为8.84%,创10年来股市跌幅最大。
第578号对应日期2007年5月30日,收益率为-7%,超过了控制下限,原因是财政部在当天0时调整证券(股票)交易印花税税率由1‰调整为3‰。
第581号对应2007年6月4日,收益率为-8%,超过了控制下限,原因于多只股票异动不停牌事件,多方唱空重挫沪深两市。
740号对应2008年1月22日,收益率为-7.9%,当日全球股市普遍遭遇“黑色星期一外围股市的暴跌,引发A股市场跟随恐慌性抛售。
801号对应2008年4月24日,收益率8.89%,超过控制上限,原因在于2008年4月24日起,调整证券(股票)交易印花税税率,由3‰调整为1‰。
831号对应2008年6月10日收益率为-8.5%,原因在于6月7日晚间,中国人民银行决定,调高存款类金融机构人民币存款准备金率1个百分点。
882号对应2008年8月20日,收益率为7.6%,超过控制上限,原因在于市场出现不少利好消息,如政府将出台千亿级的经济刺激方案,印花税调整为双向征收0.05‰,暂停三个月的新股上市审批等。
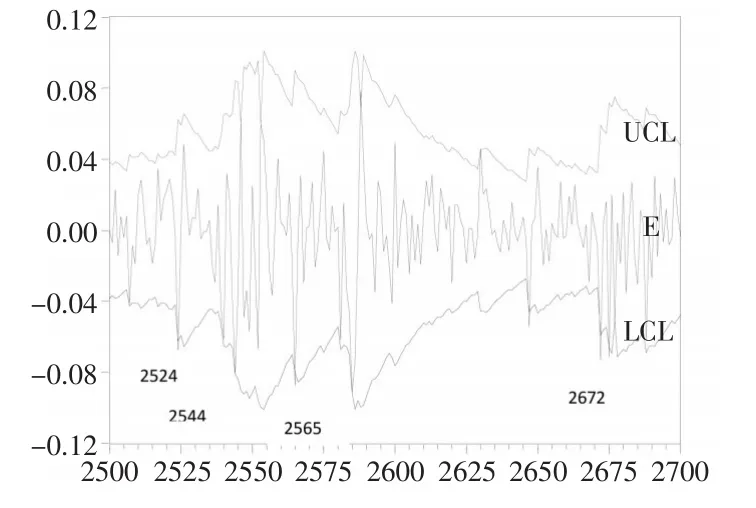
图7 2500—2700号控制图
2524号对应2015年5月28日收益率为-7%,原因在于前期股指涨幅已大,个股估值已高,此时汇金公司的减持动摇了投资者的信心。
2544号对应2015年6月26日,收益率为-8.2%,主要原因,应该是证监会严查场外配资,去杆杠的措施加剧了市场资金的紧张程度,以及部分券商已在对个人的配资买入仓位进行强制平仓清出处理,造成市场恐慌。
2565号对应2015年7月27日,收益率为-9%,原因是中字头股、券商股大幅下挫,多公司大股东违规减持,投资者信心不足。
2672号对应2016年1月4日,收益率-7.27%,当日股市暴跌,原因主要有沪深300指数熔断机制的实施,人民币对美元暴跌和油价下跌。
5 结束语
本文在传统控制图的基础上,针对时间序列的自相关性,构造了自回归AR和条件异方差GARCH模型的残差控制图,并通过GARCH残差控制图对沪深指数300数据进行了实证分析,研究表明控制图能把大部分异常数据监测出来,可以对股票市场起到很好的监控,这也为金融风险的控制提供了一个新的思路。
