建模序列数乘变换下的DDGM(1,1)模型参数特性
2019-05-05马红燕
马红燕,崔 杰,2,王 雨
(1.淮阴工学院 商学院,江苏 淮安 223001;2.南京航空航天大学 灰色系统研究所,南京 210016)
0 引言
20世纪90年代初,中国学者邓聚龙教授提出了灰色系统理论(简称灰理论)。该理论以“部分信息已知,部分信息未知”的“小样本”“贫信息”不确定性系统为研究对象,通过对部分已知信息的生成、开发,提取有价值的信息,从而对系统结构性质、演化规律进行正确描述与有效监控[1-3]。目前,灰理论在农业、工业、国防、科技、军事、教育、医疗等众多领域具有广泛的应用空间,已为经济和社会发展发挥了重要推动作用。现有研究表明,在灰建模前对系统原始特征序列进行数据变换,有利于简化建模过程[4-7]。目前,学术界部分学者对灰预测模型建模序列数乘变换前后的参数变化特征进行了研究,并取得了丰硕成果[8-14]。研究结果显示,对部分灰预测模型而言,在建模前对系统特征序列进行线性变换,可降低其建模复杂性。
灰预测是灰理论的重要分支之一。灰色GM(1,1)预测模型一直倍受学者们关注,同时亦是应用最为广泛的灰色模型之一。然而,该模型在实际应用中却时常出现预测精度不稳定的问题。目前众多文献对其进行的深入研究结果显示,该模型以差分方程建模为基础进行参数估计,而用来预测的时间响应函数却是由相应微分方程的解引申得到,从差分方程到微分方程的跨越缺乏科学依据和理论基础。鉴于此,谢乃明等[15]提出了DGM(1,1)模型,解释了GM(1,1)预测精度不稳定的主要原因,并对DGM(1,1)模型的参数进行了优化研究。然而,DGM(1,1)模型依然是基于累加的方式寻找蕴含在序列中的灰指数规律,以解释系统未来的发展趋势。而在已知建模序列为近似齐次指数序列前提下,对该序列进行累加生成往往会破坏其原有规律,降低建模精度。因此,曾波等[16]在DGM(1,1)模型基础上,提出了直接DGM(1,1)模型(简称DDGM(1,1)模型),并通过实例证明了该模型的有效性。由于DDGM(1,1)模型提出时间尚短,关于该模型参数特性的研究成果十分缺乏。研究其参数特性有利于进一步拓展DDGM(1,1)模型的应用范围,简化该模型的建模过程,提高其建模效率。鉴于此,本文以DDGM(1,1)模型为研究对象,利用三级参数包技术分析了该模型建模参数在系统特征序列经数乘变换前后的数量关系,进而揭示了该模型精度在建模序列经数乘变换前后的变化规律。
1 DDGM(1,1)模型的建模原理
定义1:设系统原始特征非负序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},则:

式(1)为直接DGM(1,1)模型,简称DDGM(1,1)模型[16]。
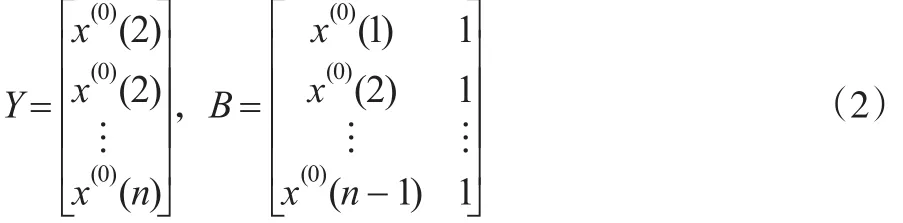

定理2:设B、Y、如定理 1所述,取则:
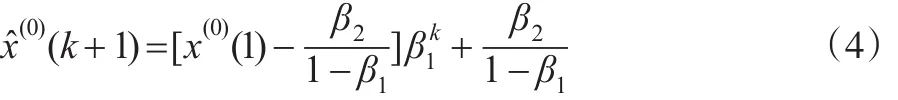
(1)称 (β1,β2)为DDGM(1,1)模型的一级参数包,记作PI:
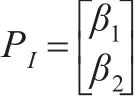
(2)称 (β1,β2)的构成成分为DDGM(1,1)模型的中间参数,其全体构成该模型的二级参数包,记作PII。
(3)称DDGM(1,1)模型的二级参数包的构成成分为基本参数,其全体构成该模型的三级参数包,记作PIII。
命题1:DDGM(1,1)模型的一级参数包PI在最小二乘准则下有如下矩阵算式:
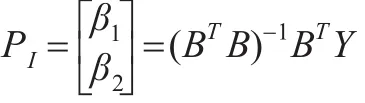
其中:
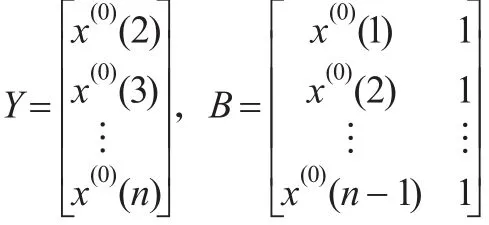
命题2:令:
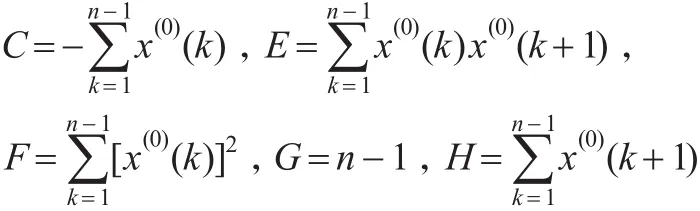
则有:
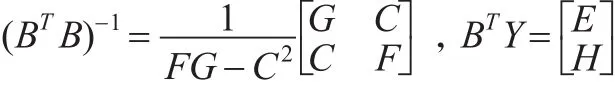
命题3:DDGM(1,1)模型的参数包有:
(1)一级参数包
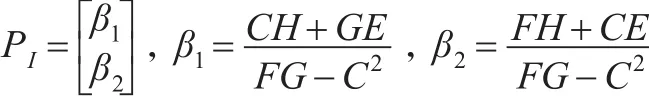
(2)二级参数包
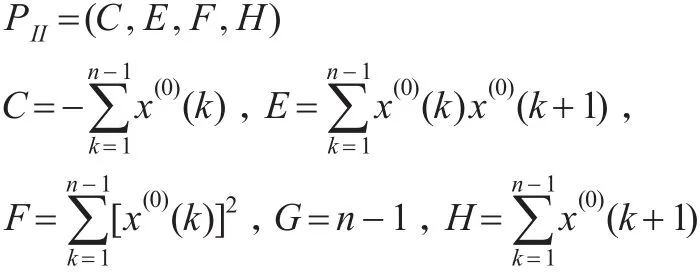
(3)三级参数包
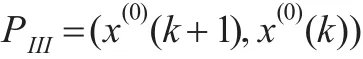
2 DDGM(1,1)模型的参数特性
定义2:对于系统原始非负数据序列Xk,Yk=ρXk,k=1,2,…,n;(ρ为常数,且ρ>0)称为数乘变换,其中ρ为数乘量。
设X(0)=(x(0)(1),x(0)(2),…,x(0)(n))为系统原始非负特征数据序列,Y(0)=(y(0)(1),y(0)(2),…,y(0)(n))为其经数乘变换后的序列。ρ为数乘量,且:
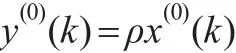
记 (β1,β2)为利用序列X(0)构建的 DDGM(1,1)模型参数序列为X(0)经数乘后的序列Y(0)构建的DDGM(1,1)模型参数序列,其他参数的定义类似。
定理3:二级参数包PII为:
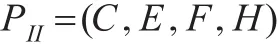
则有:
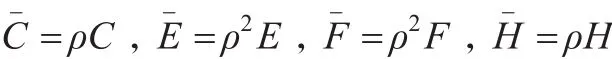
证明:

得证。
定理 4:记 (β1,β2)为利用系统特征序列X(0)构建的DDGM(1,1)模型中的参数序列,(βˉ1,βˉ2)为利用其数乘序列Y(0)构建模型对应的参数序列,则:
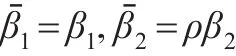
证明:
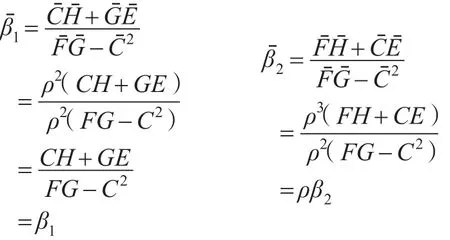

证明:
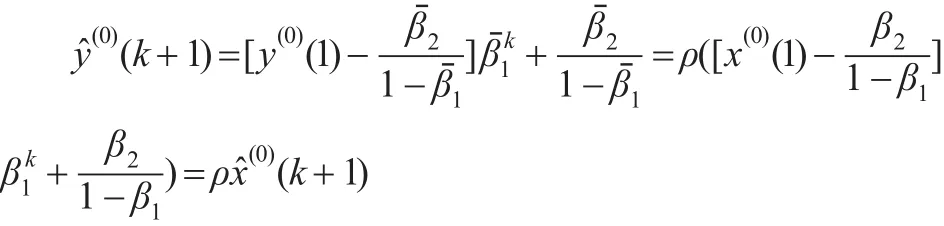
故:
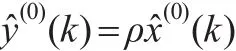
定理6:记ε(k)与εˉ(k)分别为由序列X(0)与Y(0)构建的DDGM(1,1)模型的相对误差,即:
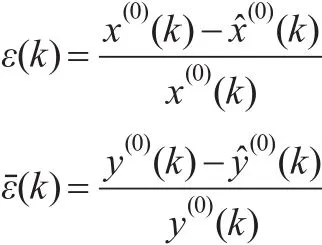
则有:
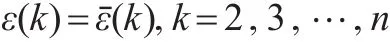
证明:
由定义2与定理5可得:
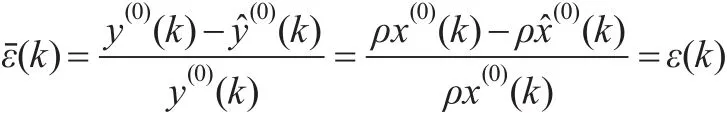
3 实例分析
设系统特征序列X(0)=(1.2,3.0,4.2,5.0,6.0,7.2)。由式(2)和式(3)可得:
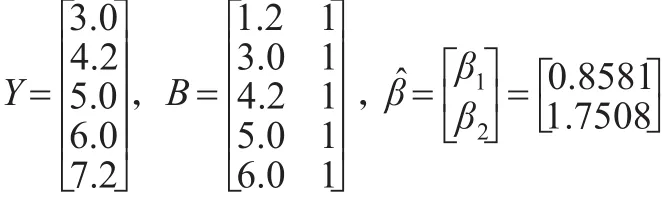
由式(4)可得:

当数乘量ρ=0.5时:
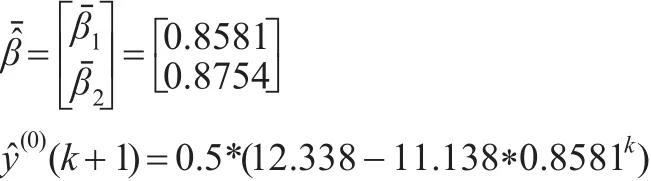
因此:
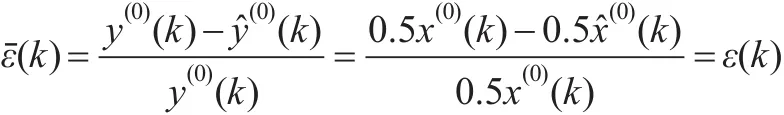
上述计算结果进一步佐证了本文的结论。
4 结束语
本文采用参数包技术对DDGM(1,1)模型建模序列经过数乘变换前后模型建模参数的量化关系及其精度变化规律进行了深入研究。结果表明,DDGM(1,1)模型的精度与其建模序列的数乘变换无关,该模型的建模精度不会因其建模序列受数乘变换作用而发生变化。因此,在DDGM(1,1)模型建模过程中,可对系统特征序列进行数乘变换预处理,进而在不改变模拟与预测精度的前提下简化其建模过程。
