基于区间犹豫模糊语言评价的多属性决策方法及其应用

龚日朝，张 文，刘东海

（湖南科技大学a.商学院；b.数学与计算科学学院，湖南 湘潭 411201）

0 引言

在现实群决策或评价过程中，运用区间犹豫模糊语言数（IVHFLN）去描述对象的每一个属性特征，关键是如何集结对象的所有被考察特征，获得科学的综合评价结论[1-3]。对此，文献[4]运用Yager（2008）提出的PA聚合算子理论[5]，构建了区间值犹豫模糊语言优先加权平均（IVHFLPWA）算子，将每个决策单元所有属性的评价结果聚合成一个新的IVHFLN，然后再通过构建IVHFLN的得分函数和精确函数选择最优决策。其权重的确定是基于对象在每个属性下的得分大小，因此，其导致不同对象的不同属性具有不同的权重，是一种“因人而异”确定属性权重的方法。显然在现实决策评价中，人们往往难以接受。此外，集结算子的理解和计算又比较复杂，在实际应用中难以得到推广运用。为此，本文转换一个决策分析的视角，将每一个对象看成是多属性维度构成的向量，在构建多维区间犹豫模糊语言数向量的距离测度基础上，运用TOPSIS方法的基本思想[6-8]，计算每一个决策单元与正理想解和负理想解的距离，构建一个新的决策过程，这就避开了文献[4]中复杂算子的构建与计算。为了验证这一方法的可行性，本文采用文献[4]的实例数据进行分析与验证，通过验证发现排序结果完全相同，充分说明本文所提出的新思路和方法能达到同样甚至更好的决策效果。

1 基本理论与假设

1.1 语言集及其语言尺度函数

定义1[9]：设是由奇数个语言元素组成的集合，其中t是一个正整数。若集合S满足两个特征：

（1）如果i＞j，则si＞sj；反之亦然。

（2）如果i+j=2t，则si=neg(sj)；反之亦然。

则称S为语言集，其中，语言元素si的个数2t+1称为语言集粒度，语言集的中点(st)为中性评价值，其他评价值以该点为中心，分别向两端对称扩展。

定义2[4]：语言集S在不同语意环境下的语言尺度函数定义为：

（1）类型A

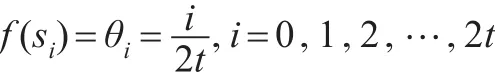
（2）类型B

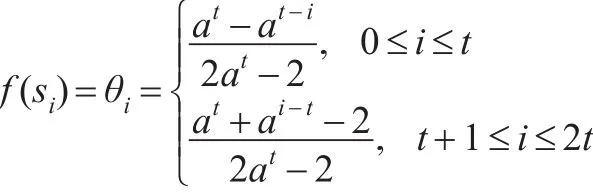
其中，a的值可以主观决定。对于7值语言集，大部分学者认为a=≈1.37比较合适。

（3）类型C

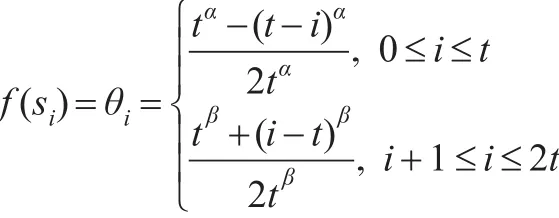
其中α，β∈(0，1]如果α=β=1，则。本文取α=β=0.8。

显然，语言尺度函数f(si)=θi是一个严格单调递增的函数。

1.2 区间犹豫模糊语言集

基于现实决策过程，文献[4]抽象出了“区间犹豫模糊语言集”的定义。

定义 3[4]：设X={x1，x2，…，xn} 为评价对象集，sθ(x)∈S是x关于属性A的评价结果，其中则被称之为一个区间犹豫模糊语言集。其中，ΓA(x)是[0，1]上有限个子闭区间的集合，即：

上式表示x关于属性A的评价为sθ(x)的有限个隶属度区间集合，#ΓA(x)表示区间个数，并称为区间犹豫模糊语言数。

注意到现实中对不同的对象x，#ΓA(x)的值可能不同。为此，本文提出如下假设：

假设：由K个成员组成的决策机构，在决策过程中每个成员必须给出自己的意见，而且采用区间数表示对象x关于属性A评价等级为sθ(x)的隶属度。但如果认为评价等级是准确的，没有异议，则可以不发表意见，默认隶属度区间为[1，1]。

显然，定义4是一种符合现实的数据处理方法，是一个由决策机构集体形成的完整决策数据，而且这一方法很好地解决了后面所要研究的多属性决策问题中数据标准化处理的问题。

1.3 IVHFLN得分函数与精确函数

基于语言尺度函数，文献[4]提出了用得分函数和精确函数刻画评价决策单元具有某属性的大小和精确性对IVHFLN排序的规则。

定义5[4]:设是 IVHFLN，其得分函数和精确函数分别定义为：

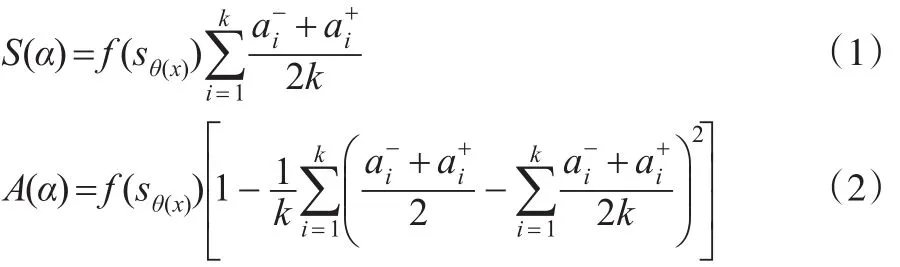
定义6[4]：设α和β为任意两个区间犹豫模糊语言数，则：

（1）如果S(α)＞S(β)，则α＞β；

（2）如果S(α)=S(β)，则：①当A(α)＞A(β)时，α＞β；②当A(α)=A(β)，则α=β。

值得一提的是，基于定义5和定义6对IVHFLN排序，α和β中的区间数个数必须相同，否则，会出现与直观认识相违背的结论。此外，如果对IVHFLN进行标准化处理，定义5中的精确函数也值得商榷，理由如下：其一，对于给定的区间犹豫模糊语言集，根据其定义，语言是确定的，其犹豫模糊性主要体现在隶属度区间的不确定性，包括区间的个数的不确定性、区间上下限值的不确定性等，因此，精确函数应该是与f(sθ(x))无关的一个测度函数。其二，精确性与隶属度区间集合中区间元素的离散程度有关，但#ΓA(x)≤K，也就是区间个数小于决策机构成员数K时，必须考虑所有决策者的意见，否则会出现与现实相违背的问题。

根据以上讨论与分析，本文对定义5进行修正，给出如下IVHFLN得分函数和精确函数的定义：

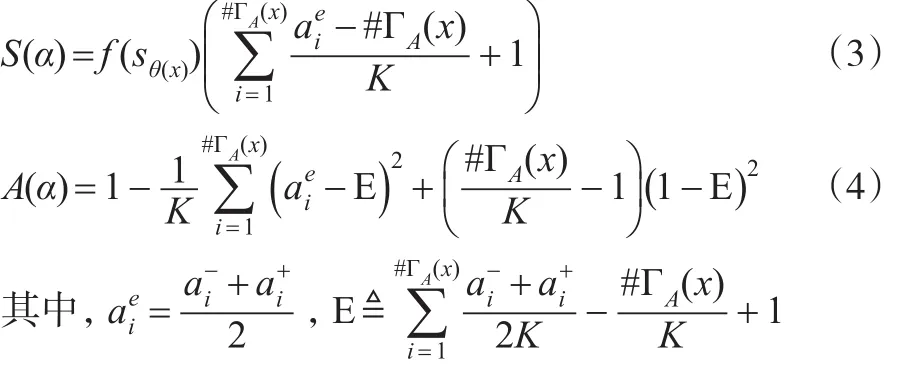
2 区间犹豫模糊语言集的多属性决策模型

2.1 问题的提出

记S={s6=很好，s5=好，s4=较好，s3=一般，s2=较差，

}s1=差，s0=很差 为7值语言术语集。

假设某多属性决策问题具有n个决策单元，由K个成员组成的决策机构D=，运用7值语言术语集对m个属性C=分别进行评价，采取两阶段决策方法，选择最优决策单元。假设属性权重为

第一阶段，由某评价机构对每一决策单元，关于每一属性给出一个评价等级。等级采取7值语言集的方法确定，得到语言数矩阵：

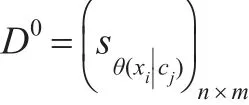
其中，sθ(xi|cj)∈S表示xi关于属性cj所对应的语言数。

第二阶段，在上述语言数矩阵D0基础上，决策机构成员分别根据个人的认知与观点，对每一个决策单元的每一个属性评价结果发表意见——给出隶属度区间，得到如下决策矩阵：

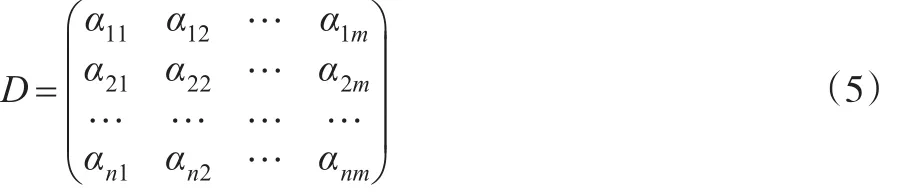
最后，基于决策矩阵，构建综合评价模型，给出最优决策单元。

2.2 区间犹豫模糊语言数向量距离测度

从决策矩阵D可以看出，矩阵每一行代表着一个决策单元的评价信息，是m维空间的一个向量。为此，本文给出区间犹豫模糊语言数向量的定义。

定义8：对于给定对象x，设1，2，…，m是属性cj的评价值，则向量称为m维区间犹豫模糊语言数向量。

决策矩阵D的n行，也可看成m维区间犹豫模糊语言数向量空间中的n个点。根据上述某个固定属性下区间犹豫模糊语言数的大小比较方法，得分函数本质上是一个区间犹豫模糊语言集到实数集合的映射。于是，通过这一映射，m维区间犹豫模糊语言数向量对应着m维得分值向量。利用欧氏空间加权向量距离公式，本文定义m维区间犹豫模糊语言数向量空间的距离侧度。

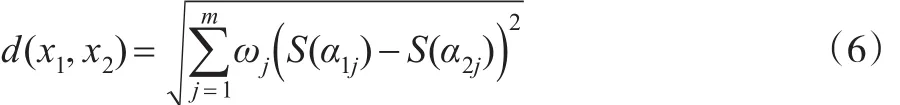
其中，ωj为权重，满足ω1+ω2+…+ωm=1，S(αij)表示区间犹豫模糊语言数αij的得分值。

根据定义9，显然有如下的定理。

2.3 TOPSIS法决策过程

基于上述理论，本文利用多属性决策问题中常用的TOPSIS方法思想，通过计算各决策单元与正理想解和负理想解的距离对决策单元进行排序，即：距离正理想解最近，且距离负理想解最远的决策单元为最佳决策单元；反之，则为最差决策单元。基本步骤如下：

第一步：建立决策矩阵（5）式，并根据定义4，将决策矩阵转化为标准决策矩阵：

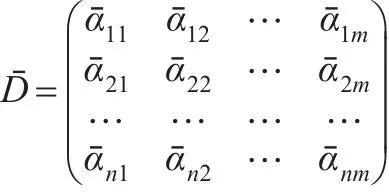
其中：

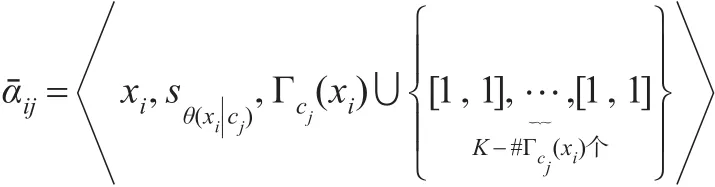
第二步：计算得分矩阵和精确矩阵。根据定义7的式（3）和式（4），分别计算每个属性下区间犹豫模糊语言数的得分函数值，得到得分矩阵和精确矩阵：

第三步：确定正理想解和负理想解。根据得分矩阵和精确矩阵，按照定义6，在标准化决策矩阵D中选择每一个属性下得分函数值最大（当最大得分值相同时，选择精确函数值最大）所对应的区间犹豫模糊语言数，记为

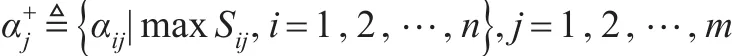
第四步：根据定义9，分别计算每个行向量（决策单元）与正理想解、负理想解之间的距离，记为d(xi，x+)和d(xi，x-)，计算公式为：

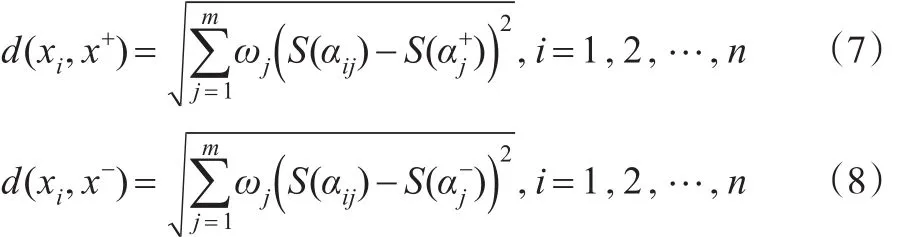
第五步：对决策单元进行排序。首先计算各个备选决策单元的相对贴近度Ci，i=1，2，…，n，计算公式为：

然后，根据相对贴近度的大小进行排序，如果某个Ci最大，则所对应的备选决策单元为最优。

3 实例数值计算结果

为了说明本文所提出方法的有效性，采用文献[4]中的实例问题和数据。

3.1 实例问题的提出

3.2 决策过程与计算结果

第一步：建立决策矩阵。海外投资部门采用7值语言集S刻画5个国家的4个属性等级，用区间犹豫模糊语言集表达每个属性的评价意见，得到区间犹豫模糊语言数决策矩阵（见表1）。

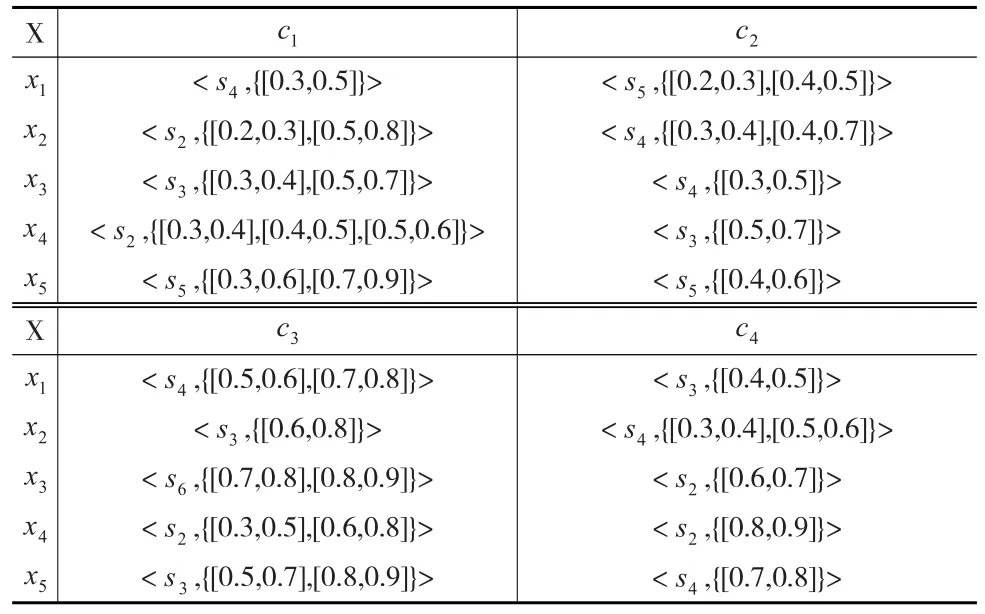
表1 区间犹豫模糊语言数决策矩阵

由表1得到标准化区间犹豫模糊语言数决策矩阵（见表2）。

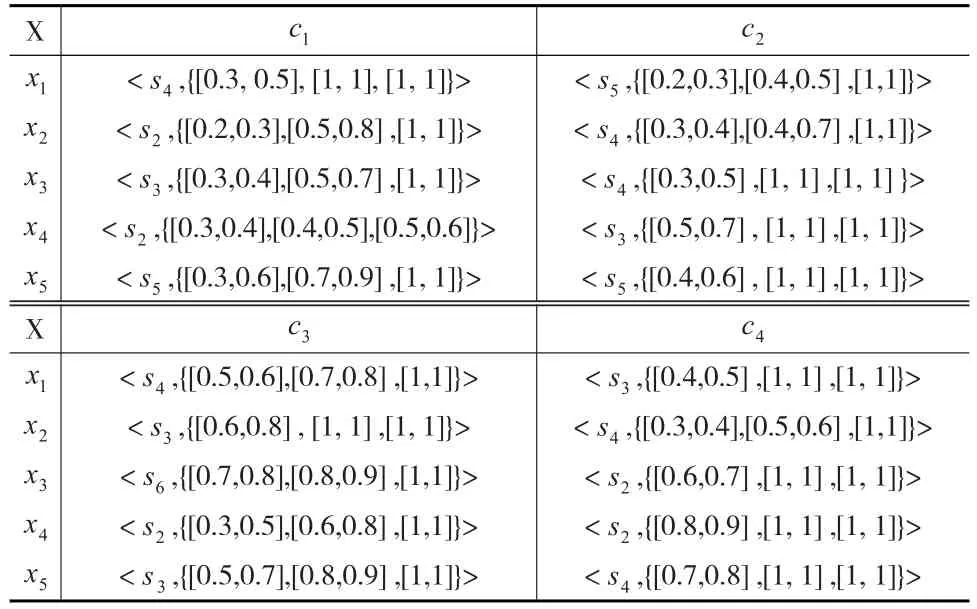
表2 标准化区间犹豫模糊语言数决策矩阵

第二步：计算得分矩阵和精确矩阵。根据表2标准化决策矩阵，运用定义7的式（3）和式（4），分别计算每个属性下区间犹豫模糊语言数的得分函数值，分别得到定义2中三种尺度函数下的得分矩阵（见表3）。

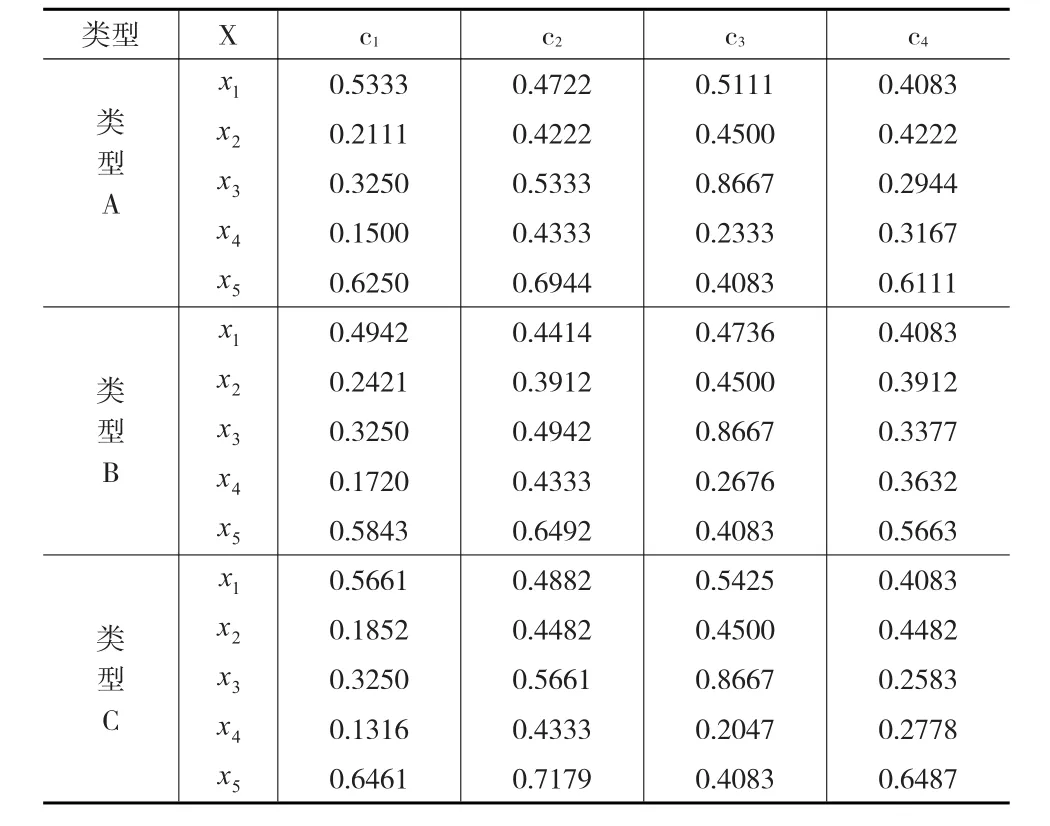
表3 三种类型尺度函数下的得分矩阵

第三步：确定正理想解和负理想解。根据得分矩阵（表3），在三种类型尺度函数情形下，可获得正理想解和负理想解（见表4）。

表4 三种类型尺度函数下的正理想解和负理想解

第四步：假设四个属性 {c1，c2，c3，c4} 的权重对应为{ω1=0.73，ω2=0.18，ω3=0.06，ω4=0.03}，根据式（7）和式（8）计算每个备选决策单元与正理想解和负理想解之间的距离，并根据式（9）计算出相对贴近度，结果见表5。

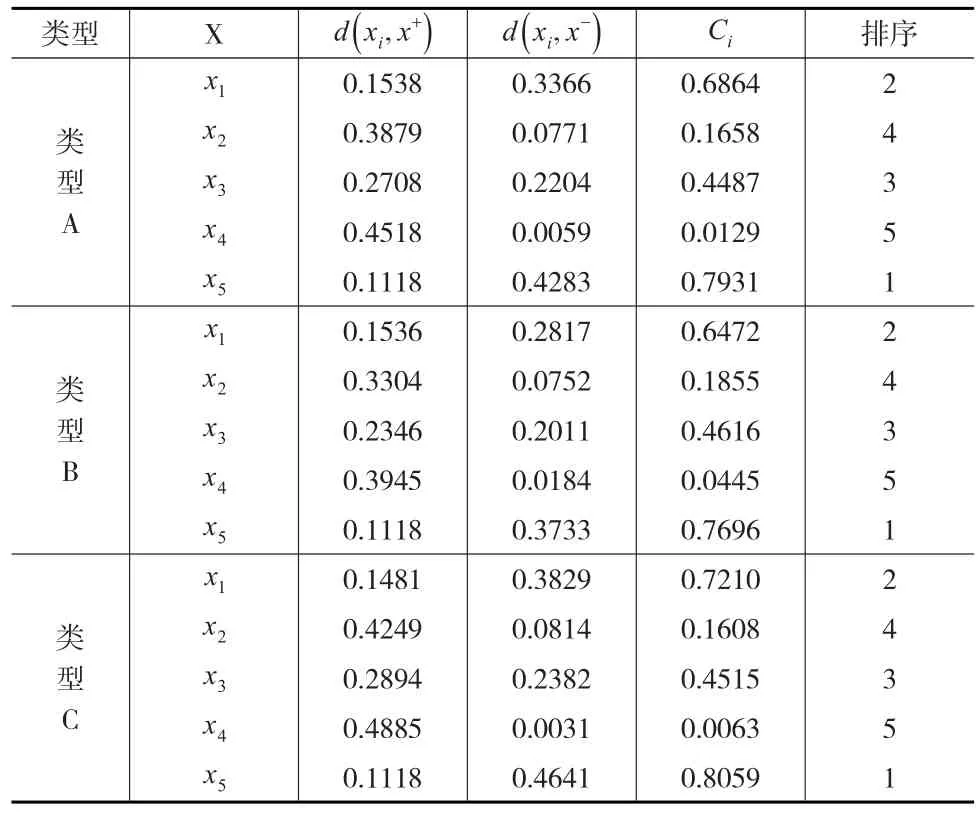
表5 三种类型尺度函数下决策单元与理想解的距离及相对贴近度

由表5可以看出，5个决策单元的排序，均为x5≻x3≻x1≻x2≻x4，表示x5为最佳投资对象，其次是x3，而x4是最不理想的投资对象。这一结论与文献[4]的结论完全一致，充分说明本文提出的决策方法与过程同样是有效的，而且更简单直观。

4 结束语

本文运用向量距离测度法，结合现实群决策过程，首先定义了标准化区间犹豫模糊语言数以及其向量的概念，实际上，也就是给出了一种区间犹豫模糊语言数的归一法，并据此修正了文献[4]提出的区间犹豫模糊语言数的得分函数和精确函数计算公式。然后，利用得分函数将区间犹豫模糊语言集映射到实数集的关系，构建了区间犹豫模糊语言数向量之间的距离测度，实现了将区间犹豫模糊语言数决策矩阵向实数矩阵的转换。通过这些方法的创新，本文有效地运用了多属性决策中常用的TOPSIS方法思想，建立了基于区间犹豫模糊语言评价的多属性决策模型，大大简化了文献[4]构建PA聚合算子的决策计算过程。通过运用文献[4]中的同一问题及其数据进行决策计算与分析，本文得到了与其完全相同的决策结果，验证了方法的有效性和可行性。显然，本文决策过程更容易被人们理解和接受，在现实中更容易被应用，而且也进一步有利于被决策对象分析自身的优势和存在的不足。