一种弹载三轴加速度计现场快速标定及补偿方法

冯凯强，李 杰，魏晓凯

(中北大学 仪器科学与动态测试教育部重点实验室， 太原 030051)

在惯性导航系统中，三轴加速度计性能的好坏直接影响到惯导测试系统的速度、姿态、位置解算精度，因此，对加速度计的测试标定已成为惯性测量组合使用过程中的重要环节[1]。对于三轴加速度计而言，通常由3个两两相互正交的加速度计组成，其测量精度与传感器的零偏、刻度系数以及敏感轴之间的不正交安装误差相关[2]。在应用过程中，需对传感器输出进行标定补偿以提高系统的测试精度。传统三轴加速度计的标定方法需要借助光学分度头或三轴转台等高精度测试设备来获得准确标定参数。大量试验表明，惯性器件自身性能参数会随时间的推移与应用环境等方面的变化而发生变化[3]。最为显著的就是传感器的零位漂移，与初始标定时间相隔越长，传感器的零漂越明显；若在后期应用过程中沿用原有的标定结果，则会产生较大的解算误差。实验表明，加速度计的零偏对导航计算结果的误差影响按时间的二次方增长。因此，弹载惯性测量组合在靶场实验环境中传感器自身性能参数与实验室环境中转台标定参数会有很大不同，实弹飞行测试中，惯性测量单元中传感器输出参数误差会产生较大的解算误差，影响惯性测量组合的测试精度。由于火箭弹、炮弹等常规武器飞行时间短，因此与弹体固联的惯性测量单元在较短的工作时间内需要有准确的参数输出，以提高导航计算机的解算精度，在靶场实验环境中，不可能实时利用转台等精密设备对安装于弹体中的惯性测量组合进行在线标定，而通过滤波算法实现的系统级标定方法因其可观测性分析复杂，计算量大也无法达到有效应用。鉴于此，本研究提出了一种三轴加速度计在线快速标定方法。该方法无需依赖转台等精密仪器，根据椭球拟合算法实现三轴加计的参数标定，并结合加速度计输出特点给出了具体的标定位置编排，完成了相应的误差补偿。

1 三轴加速度计误差分析

针对单轴加速度计，其测量误差主要由零偏、灵敏度误差和随机漂移误差组成。加速度计的随机漂移误差通常由偏置误差与白噪声组成，由于标定时间短，加速度计等效漂移往往经过后期滤波处理获得，在标定时往往忽略该项。因此，各轴加速度计的测量模型通常表示为

Uai=Kiai+Uai0

(1)

其中：Uai为i轴加计输出电压值；Ki为i轴加速度计实际灵敏度；ai为i轴加速度真实值；Uai0为i轴加速度计的零位偏差。在弹载微惯性测量组合中，三轴加速度计通常由3个两两相互正交的加速度计组成，用来敏感加速度矢量在坐标系下的投影[4]。理想状况下，可得到三轴加速度计的测量模型为

(2)

但是在制造过程中，由于安装误差的存在，无法保证三个传感器的测量轴两两完全正交[5]，其不正交示意图如图1。

图1 不正交示意图

假设OX0Y0Z0为理想三轴正交坐标系；OXYZ为实际加速度计敏感轴系；其中，Z轴与Z0轴重合，X轴在X0OZ0内与X0的夹角为α；Y轴在X0OY0内与Y0的夹角为β；Y轴与X0OY0面的夹角为γ。建立三轴加速度计的不正交误差模型如下

(3)

综上所述，三轴加速度计误差主要有加速度计零偏、灵敏度误差和不正交误差，由此建立三轴加速度计的测量模型为：

Ua=Ka+Ua0

(4)

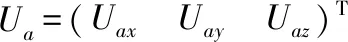
2 三轴加速度计在线标定模型

由于同一地点的重力加速度为一个常值，理想情况下，静止放置的三轴加速度计在不同姿态下测得的加速度分量在三维空间中可构成一个中心在原点半径为当地重力加速度的标准球体[5]。但由于三轴加速度计各项误差的存在，使得形成的球体发生偏离，变为中心偏离原点的椭球。即：

aTa=[K-1(Ua-Ua0)]T[K-1(Ua-Ua0)]=g2

(5)

由上式变换成椭球曲面的二次型方程为：

(6)

三轴加速度计在线标定模型的实质就是通过测定不同姿态下三轴加速度分量拟合椭球的中心坐标与形状参数来获取加速度计的各项误差参数[6]。椭球曲面的一般方程为：

F(ξ,Z)=ξTZ=0

(7)

式中：椭球曲面参数ξ=[a,b,c,d,e,f,p,q,r,g]；设Z=[x2,y,z,2xy,2xz,2yz,2x,2y,2z,1]T为采集数据运算组合向量；F(ξ,Z)为采集数据(x，y，z)到椭球曲面的代数距离。

在进行二次曲面拟合时，采用带约束的最小二乘法的椭球拟合一般选择测量数据(x，y，z)到二次曲面代数距离的平方和最小为判断准则，为了确保最终拟合的二次曲面为一椭球体，引入约束条件：

(8)

则得到拟合后的最佳椭球曲面方程整理为矢量形式为

(X-X0)TA(X-X0)=1

(9)

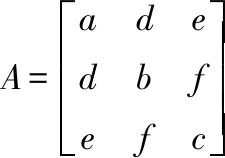
通过对比式(6)与式(9)可以得到

KKT=A-1/g2

(10)

Ua0=X0

(11)

根据式(4)可以计算得到各标定参数的估计值为

(12)

结合上述公式，利用拟合的得到的椭球参数即可获得三轴加速度计的零偏和误差系数矩阵，完成加速度计的标定。

3 在线标定方案编排与误差补偿

基于椭球约束的最小二乘法拟合原理的实质是找到一组最佳椭球参数，使得测量数据到椭球曲面的距离达到最小[7-8]。对用于拟合的测量数据来讲，要求该数据尽可能地覆盖椭球曲面的绝大部分球面，并且数据正确反映各测量轴的重力分量[9-12]。标定过程中通常在三维空间内采用画8字的方式进行椭球分布，但是由于加速度计干扰噪声以及响应时间等因素限制，对于单点采样得到的测量数据会出现杂质点，无法获得准确的标定参数。

因此，依据传感器的输出特点以及拟合要求制定出如下标定方案：

1) 待传感器上电稳定后，在待标定固定位置点测量当地重力加速度；

2) 依据三轴加速度计在载体上的安装方式(X轴对应载体滚转轴)，分别在俯仰45°、0°、-45°时，各绕滚转轴旋转一周；每周大致设置8个等分测量点，在每个测量点处静止采集20 s；

3) 再次随机旋转载体，使其所处姿态对应测量点尽量覆盖其余椭球曲面，每个测量点处静止采集20 s；

4) 选取步骤2)、3)中得到的每段测量值的稳定数据求取均值，并保存为样本数据；

5) 将步骤4)得到的数据拟合椭球曲面，获得拟合椭球的中心点坐标与形状参数；

6) 计算三轴加计的待标定参数，完成参数输出。

在误差模型的基础上，由式(4)可得三轴加速度计测量校准模型为

a=K-1(Ua-Ua0)

(13)

式中：

为误差补偿系数矩阵。

根据式(12)利用拟合得到的椭球参数计算标定数据，将标定结果代入式(13)，即可得到三轴加速度计的测量校准模型，利用该模型对三轴加速度计的测量结果完成误差补偿。

4 验证

为了验证该标定补偿方法的可行性、有效性，以实验室自行组建的惯性测量组合与采集存储电路为测试平台，如图2所示，利用高精度三轴位置速率温控转台进行了静态标定实验验证。

图2 测试平台

本实验室自行组装的惯性测量组合在X、Y、Z三轴分别集成有量程为±10 g的加速度计，根据3.1节中的标定方案对三轴加速度计进行现场标定试验，并以5 kHz采样率对传感器输出进行采集存储。

根据上述三轴加速度计的在线标定模型，利用MATLAB软件对试验数据进行数据处理，拟合得到的最佳椭球曲面如图3所示，其中椭球拟合残差表示选取样本数据与拟合数据之间的偏差，如图4所示，若出现残差过大的奇异点，证明该点数据测量时可能受到误差干扰，将其滤除后重新拟合。最后根据所得椭球的形状参数解算得到三轴加速度计的各项标定参数如下：

kx=0.218 25 V/g，ky=0.208 58 V/g，kz=0.217 19 V/g，Uax0= 2.509 76 V，Uay0= 2.512 98 V，Uaz0= 2.495 36 V，α=1.234 7°，β=-0.865 3°，γ=0.342 5°。

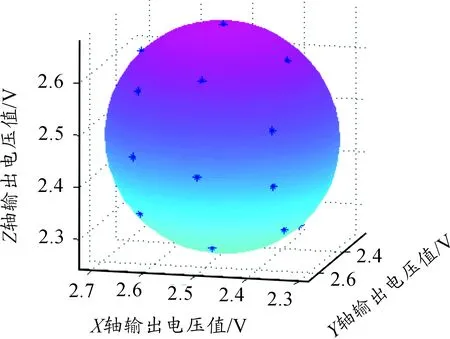
图3 三轴加速度计输出

图4 椭球拟合残差

由以上获得的标定参数计算得到三轴加速度计的误差补偿系数矩阵为

将惯性测量组合放置在三轴高精度位置速率转台上，根据三轴加速度计在载体上的安装位置，将X轴和Z轴设置为水平状态，Y轴敏感重力加速度，如图5所示，进行多次采集试验。

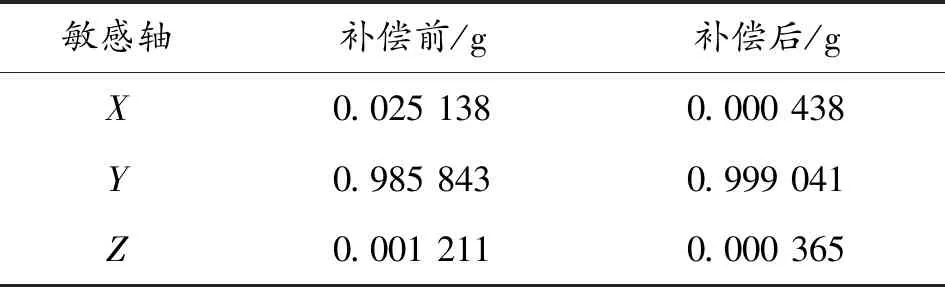
应用上述误差补偿矩阵对三轴加计输出进行补偿，其补偿前后加速度计输出对比曲线如图6所示，对比数据如表1所示。

图5 转台实验

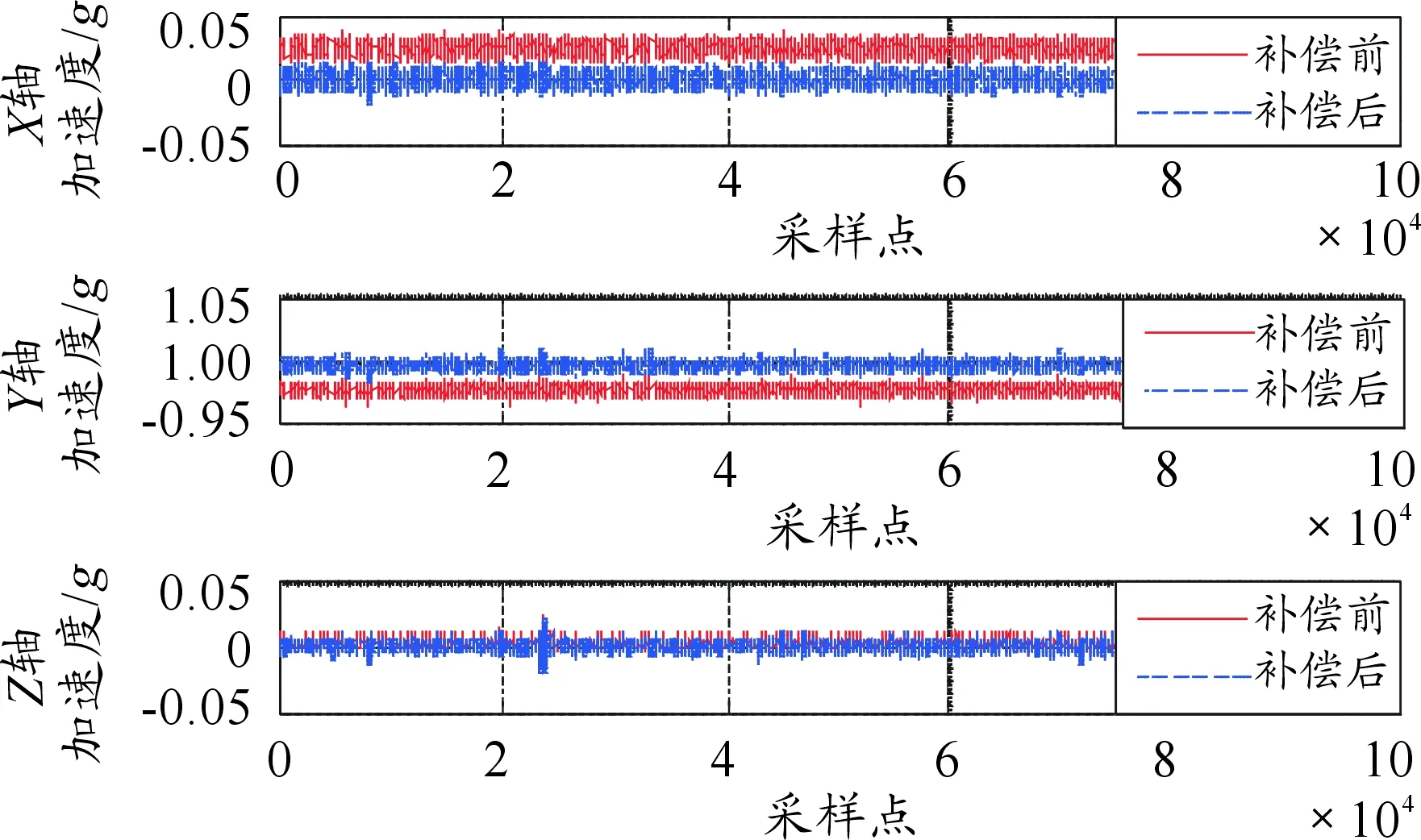
图6 补偿前后三轴加速度

敏感轴补偿前/g补偿后/gX0.025 1380.000 438Y0.985 8430.999 041Z0.001 2110.000 365

由表1可得补偿后的三轴加速度测量值与补偿前相比，补偿后三轴加速度测量误差均小于1 mg，其补偿效果与转台标定效果基本吻合，满足标定精度要求。在现场标定过程中随着拟合样本数据的增加，使得测量数据尽可能全面地覆盖拟合椭球曲面，其标定效果能够与转台标定效果相当。实际应用中，由于加速度计零位和灵敏度随时间推移而发生变化，对后期数据解算带来的较大计算误差，因此应用现场标定得到的零偏及其误差补偿系数矩阵对传感器输出进行误差补偿满足实际数据解算需求。

5 结论

1) 对三轴加速度计输出信号进行标定补偿是提高惯性导航系统位置测试精度的有效途径之一。

2) 针对三轴加速度计的零偏与灵敏度等各项标定参数因时间推移而无法得到有效应用，依据最小二乘法的椭球拟合原理实现对三轴加速度计测试标定，得到三轴加速度计的零位、灵敏度以及不正交安装误差角，无需精密的测试标定设备，修正过程简单且易于实现，标定效果与转台标定效果相当，补偿精度满足实际数据解算要求，适合在载体在线快速标定，具有较高的工程应用价值。