虚拟重联条件下地铁列车追踪运行性能衡量
2019-05-05陈明亮董海荣
荀 径,陈明亮,宁 滨,唐 涛,董海荣
(北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
随着世界各地经济的发展,工业化的程度不断提高,城市人口急剧膨胀,交通堵塞已成为一种世界性的弊端,特别是大、中城市的交通拥挤现象不容乐观,现有的地铁、轻轨等轨道交通作为一种解决城市
拥堵的有效手段,在城市公共交通中发挥骨干作用.但是建造新的线路不仅造价昂贵而且国土资源有限不能无限制的建造,为了满足不断增长的出行需求,提升既有线路运行效率已成为国家战略和人民生活的迫切需要[1-2].未来轨道交通的发展方向之一可以从列车运行编组方式的角度考虑,应用先进的列车编组系统或先进的闭塞制式系统来提升轨道交通的运输效率,缩短列车之间的发车时间间隔,提高列车的运输能力,因而达到满足交通运量需求和国民经济发展需要的目的.
文献[1]将虚拟重联的概念概括为两列或多列具有类似制动性能的列车保持一定的较短距离运行,相互之间通信、加速和减速操作保持一致. 文献[2]提出希望能借助于已掌握的高科技手段, 控制前后车辆(列车)的间隔, 形成一种无形软连结的速度联控的状态, 在确保安全的前提下, 最大限度地实现高速度、高密度结队运行, 发挥线路最大的通过能力,这种协调多列车速度,高密度、高速度结队运行的思想与虚拟重联概念有类似之处.国内一些学者也开展了列车虚拟重联运行相关的研究.文献[3]提出基于独立列车模块的“virtually coupled train formations(虚拟重联列车编队)”的设想.列车之间连接不再是实际的物理车钩,而是通过车与车之间相互通信,保持较短的距离在一起编队运行.这是虚拟重联列车运行制式的雏形.文献[4]指出当前列车编组已经成为一个重要的制约运输性能的因素,许多情况下列车编组会因为车辆型号或版本的不同而无法进行.提出虚拟重联通过无线通信的方式来达到类似于实际物理结构连接的效果,笼统地介绍了虚拟重联的含义以及实现虚拟重联所需要的工业技术,并分析了这些虚拟重联关键技术未来需要发展的趋势和方向.文献[5]提出ETCS Level4的设想,通过一种“running closer(跑的更近)”或者被称作“relative block(相对闭塞)”的原则,列车和列车之间的距离不再是根据前车的绝对位置而是相对速度和相对位置来决定,文献中探讨了该系统可能的样貌,并描述了该系统在实际运行中将会面临的一系列的安全性、技术性、业务性和文化性的挑战以及潜在的优势.文献[6]根据日本高速铁路新干线的实际情况,提出在列车运行中实现列车的编组和解编,并针对具体的应用场景去实现列车的虚拟重联.提出了一种新型的通过式道岔概念,即列车可以在道岔处自由选择方向,这种道岔极大地方便虚拟重联的应用.再利用DLR(德国宇航中心)的仿真工具DFSimu仿真了虚拟重联的一些方案,得出虚拟重联能够提升线路通过能力.文献[7]着重于从通信技术的角度考虑实现虚拟重联需要在低延迟下列车与列车之间分享位置速度信息.文献中通过拓展利用IEEE 802.11p应用到列车动态编组上,利用仿真分析探讨了IEEE 802.11p在汽车与汽车通信和列车与列车之间通信的性能,并且把一些应用在汽车与汽车之间通信的抗干扰手段移植到列车之间通信中分析其效果.得出通过增加发射功率、减小包长度或者使用定向天线能够提高抗干扰能力的结论.文献[8]提出顺序接发式、队内越行式、编队被穿行式和编队侧线让行式列车编队通过车站的4种形式.通过对每种形式特性进行的详细计算和分析,说明引入列车编队运行方式能够有效缩小列车在车站区域的追踪间隔,但该研究针对干线铁路中存在多条站线的车站.通过分析,得出虚拟重联是一种列车编队运行的方式.当多列列车基于无线通信和协同控制,从独立运行自动地进入虚拟重联运行的状态,这个过程称为虚拟编组.当虚拟重联运行时,列车安全制动模型是安全防护的基础.
本文作者提出了一种基于虚拟重联的追踪模型(以下简称虚拟重联模型),在此基础上与移动闭塞、相对移动闭塞和车站追踪改进模型进行了对比,通过数值模拟计算分析比较4种追踪模式的车站通过能力大小.运用Matlab建立列车运行仿真系统,通过仿真研究4种不同追踪模式的列车延误传播情况,从而分析其整体的延误情况和系统对延误的吸收和恢复能力.
1 安全制动模型
1.1 经典安全制动模型
根据IEEE基于通信的列车控制系统(Communication Based Train Control System,CBTCS)性能和功能要求标准的规定[9],CBTC经典安全制动模型是由保障紧急制动率(Guaranteed Emergency Brake Rate,GBER)紧急制动曲线、列车自动防护(Automatic Train Protection,ATP)超速检测曲线和ATP轮廓曲线组成,具体情况见图1.
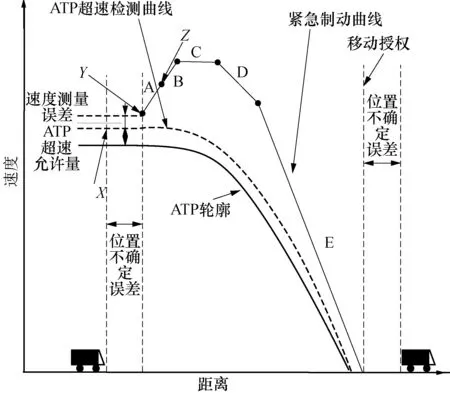
图1 典型安全制动模型Fig.1 Typical safe braking model
典型安全制动模型的GEBR曲线是由5个阶段构成.A阶段为车载CBTC响应阶段:在该阶段,列车假设以最大速度保持加速行驶,直至ATP检测到列车速度已经超出ATP紧急制动触发曲线,开始启动紧急制动.B阶段为牵引系统切除阶段:在该阶段,列车牵引力逐渐取消,列车的加速度从最大降为零,列车依然保持加速运动.C阶段为惰行阶段:在该阶段,列车既没有牵引力也没有制动力,继续以最大速度运行.D阶段为紧急制动建立阶段:在该阶段,列车的制动系统开始发挥作用,制动率从零增加到制动率最大满足GEBR曲线斜率为止.E阶段为GEBR制动阶段:在该阶段,列车以最大制动率制动到列车停稳为止.X点为车载ATP测定的速度/位置,Y点为牵引力开始失控的实际速度位置,Z点为ATP引发的紧急制动.
1.2 考虑相对速度的安全制动模型
经典安全制动模型始终假定前车是静止状态,以此为条件计算后车的移动授权,这种方式虽然安全但牺牲了效率.只单独考虑列车自身的制动模型远远达不到虚拟重联所需要的安全距离,因此需要考虑和附近列车的协同控制问题.具体情况见图2.
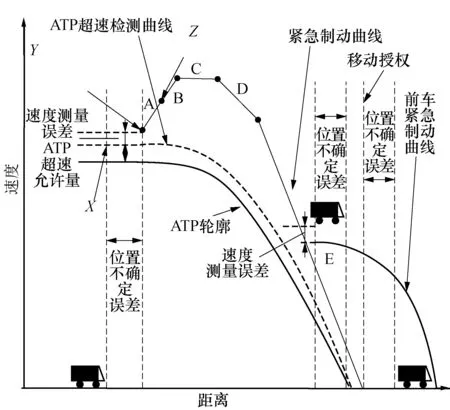
图2 考虑相对速度安全制动模型Fig.2 Safe braking model of considering relative speed
在前车有一定速度的情况下,利用考虑相对速度安全制动模型,列车与列车之间的安全间隔距离会得到有效的缩短,这种情况就像汽车的车辆编队一样.而且前方列车速度越大,安全间隔与经典安全制动的安全间隔相比缩短的越大.这种安全制动模型适用于虚拟重联两列或多列列车速度控制的场景,为虚拟重联列车组的安全性提供一定的保障.
2 列车车站追踪间隔模型
2.1 移动闭塞车站列车追踪间隔模型
在移动闭塞条件下,前后两列车的最小安全间隔是指:前行列车刚刚安全驶离出车站,且驶过安全保护段LS,后续追踪列车则以区间最大允许速度vmax运行,并且距车站入口的距离正好等于列车制动距离加上制动反应时间内列车驶过的距离[10].如图3所示. 图3中TR是列车司机、列车车载设备与地面设备等的反应时间,b为列车制动减速度,LT是列车的长度.

图3 移动闭塞条件下车站追踪间隔时间示意图Fig.3 Station tracking interval under moving block
结合文献[10],列车在站台有停留时间的情况下,移动闭塞下列车车站追踪间隔时间为
(1)
式中:a为列车启动加速度,m/s2;TD为列车车站停留时间,s.
2.2 相对移动闭塞车站列车追踪间隔模型
在相对移动闭塞制式中,由于追踪列车考虑了前车的行驶速度,前行列车在通过出站保护区段时,只要到达某一特定位置,在该位置即使前车进行了紧急制动,从该位置到紧急制动停稳所行驶的距离加上制动前正常运行行驶的距离超过安全防护区段距离的大小,即可视为列车通过了安全保护区段,如图4所示.

图4 相对移动闭塞条件下车站追踪间隔时间示意图Fig.4 Station tracking interval under relative moving block
类似移动闭塞,可以得到相对移动闭塞制式下列车车站的追踪间隔时间为
(2)
2.3 虚拟重联车站列车追踪间隔模型
虚拟重联模型,两两列车虚拟重联为一列“虚拟重联列车组”,每个列车组内行驶在前方的列车称为头车,行驶在后方的列车称为尾车.尾车保持相对移动闭塞的追踪模式与头车保持很短的安全距离,列车组中的两列列车同时在车站发车同时到站,而且需要拥有足够大的站台能够同时容纳两列列车. 列车组外,列车组与列车组之间采用移动闭塞的追踪模式行驶,具体情况如图5所示.

图5 虚拟重联模型下车站追踪间隔时间示意图Fig.5 Station tracking interval under virtual coupling prototype
结合式(1)可以得到虚拟重联模型列车车站的追踪间隔时间为
(3)
2.4 改进的车站列车追踪间隔模型
虚拟重联模型和列车重联运行的思想很相近,它是一种能够迅速扩充运能的措施,但是受到车站站台等因素制约难以在实际中应用,因此本文在此只作为偏向理论的讨论.于是引入车站追踪改进模型,使列车在车站以相对移动闭塞制式的方式追踪运行.
车站追踪改进模型,在车站区域内所有列车均采用相对移动闭塞追踪,在区间采用移动闭塞追踪.这里车站区域具体是指前行列车出站时的车尾和后续追踪列车开始减速进站时车尾之间的位置,见图3.由于车站区域采用的是相对移动闭塞的追踪方式,其车站追踪间隔时间与相对移动闭塞的车站追踪间隔时间相等.即
T4=T2
(4)
3 性能衡量与结果分析
3.1 稳态性能衡量
仿真参数设置如下:列车长度LT=140 m;防护区段长度LS=15 m;列车启动加速度a=1 m/s2;列车制动减速度b=1 m/s2;制动反应时间TR=3 s;停站时间TD=20 s.
基于式(1)~式(4),可以得到移动闭塞、相对移动闭塞、虚拟重联模型和车站追踪改进模型的车站追踪间隔时间与列车运行速度的关系,仿真结果如图6所示.
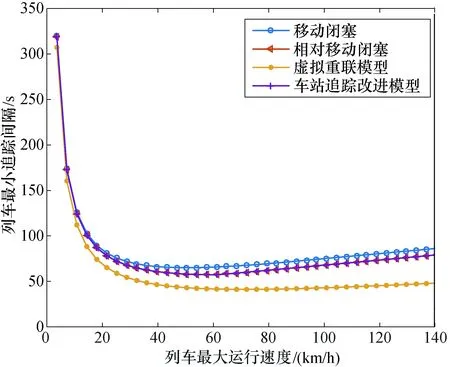
图6 不同追踪模式下车站追踪间隔时间对最大运行速度的影响Fig.6 Effect of maximum speed on cross-platform minimum headway with various tracking models
在列车追踪运行的情况下,计算线路的通过能力的一般公式为[11-12]
(5)
式中:N为线路在1 h内能通过的最大列车数,列;t为列车最小追踪间隔时间,s.
列车最小追踪间隔时间的控制值一般发生在前行列车停站作业过程中.当多辆列车沿同一轨道同一方向依次行驶时,后续列车与前行列车间必须有足够的追踪间隔时间,使相邻列车间保证有一定的安全距离,从而避免后续列车产生非正常制动和停车或发生碰撞.因此本文中利用车站的追踪间隔时间计算线路的通过能力.线路通过能力忽略了实际情况下线路运营中的很多影响能力的因素,因此这里仅作为理论上能力的上界讨论.不同追踪模式下线路通过能力与列车最大运行速度的关系见图7.
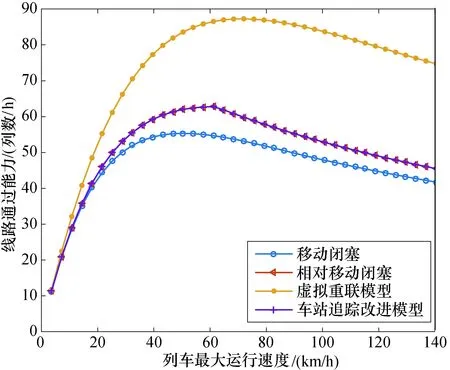
图7 不同追踪模式下通过能力对最大运行速度的影响Fig.7 Effect of maximum speed on capacity under various tracking modes
在vmax=72 km/h时,不同追踪模式下车站追踪间隔时间和通过能力见表1.
从图6和图7中可知,车站列车追踪间隔时间不是速度越大,间隔时间越小,而是在某一个特殊的速度条件下,追踪间隔时间达到最小.在超过这个速度限制后,速度越大,车站的追踪间隔时间将会越来越大,相应的理论通过能力也越来越小.根据仿真所得数据表1可得,同等最大行驶速度限制下,移动闭塞车站追踪间隔时间最大,车站追踪改进模型和相对移动闭塞的追踪间隔相等,虚拟重联模型的车站追踪间隔时间最小.对应的通过能力虚拟重联模型最大,相对移动闭塞和车站追踪改进模型相等,移动闭塞最小.由此可见,在移动闭塞制式下,加入虚拟重联模型和车站追踪改进模型的概念,都将在理论上提升一定的线路通过能力(表1的数据中,虚拟重联模型相较于移动闭塞提升了64.1%的通过能力,车站追踪改进模型相较于移动闭塞提升了11.3%的通过能力).这只是两两列车编组,如果实现更多列列车编组,线路通过能力方面还将得到进一步的提升.但是相应的,列车控制系统将会更加复杂化.

表1 不同追踪模式下车站追踪间隔时间和通过能力比较Tab.1 Comparison of cross-platform minimum headway and capacity under various tracking modes
3.2 动态性能衡量
3.2.1 列车运行仿真模型介绍
本文中所用的列车运行仿真模型,是参考文献[13-16],利用元胞自动机模型建立不同闭塞制式下列车运行的仿真模型,来研究列车在车站的运行规律.假设线路轨道是由L个格子组成,每个格子大小相同.系统的时间是离散的.列车速度在0至vmax之间取整数.模型中列车在每一时步的速度和位移更新规则如下:
当vn>vc,则vn→vn-b;列车处于制动状态xn→xn+vn·t-0.5·b·t2.
当vn=vc,则vn→vn;列车处于惰行状态xn→xn+vn·t.
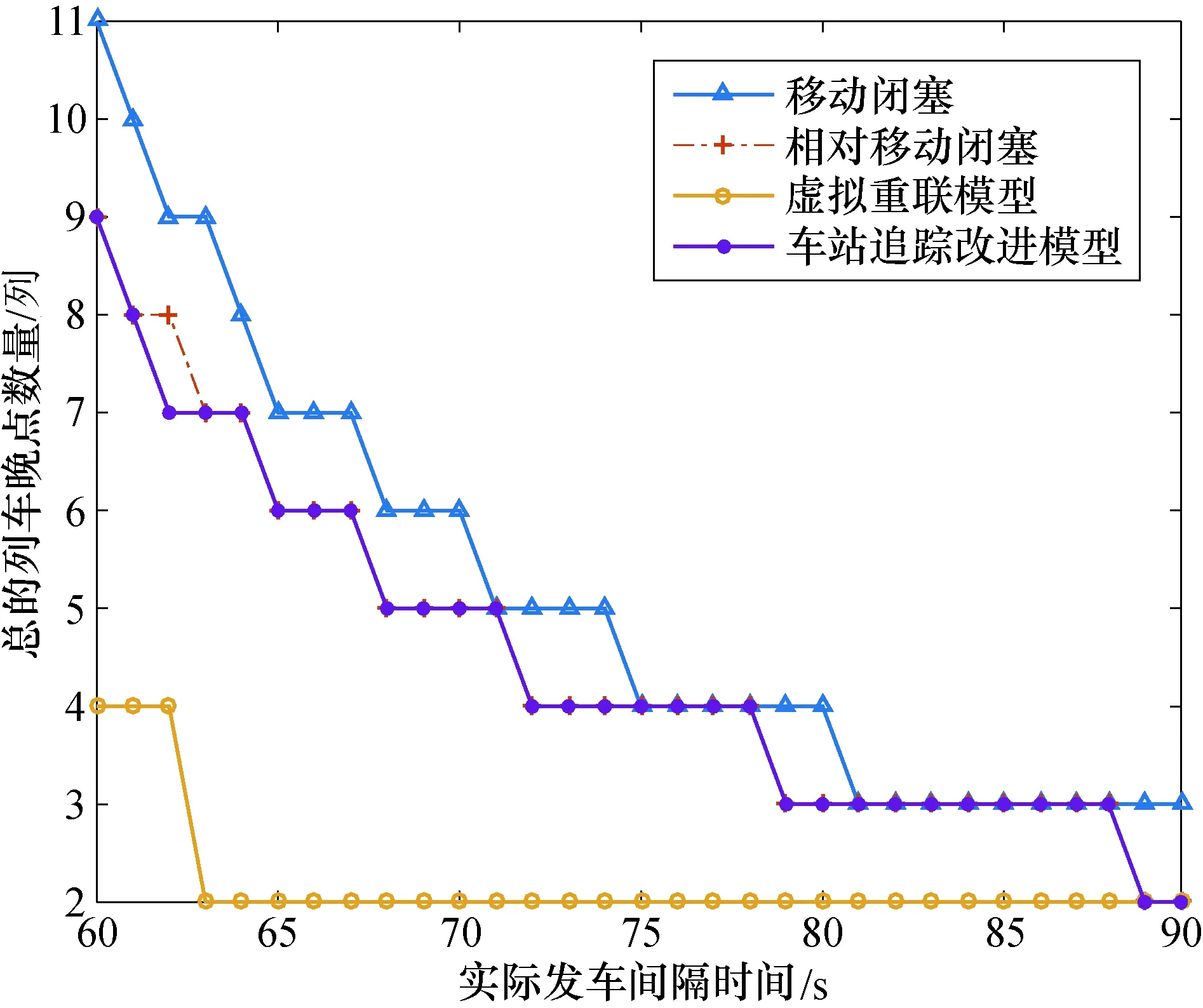
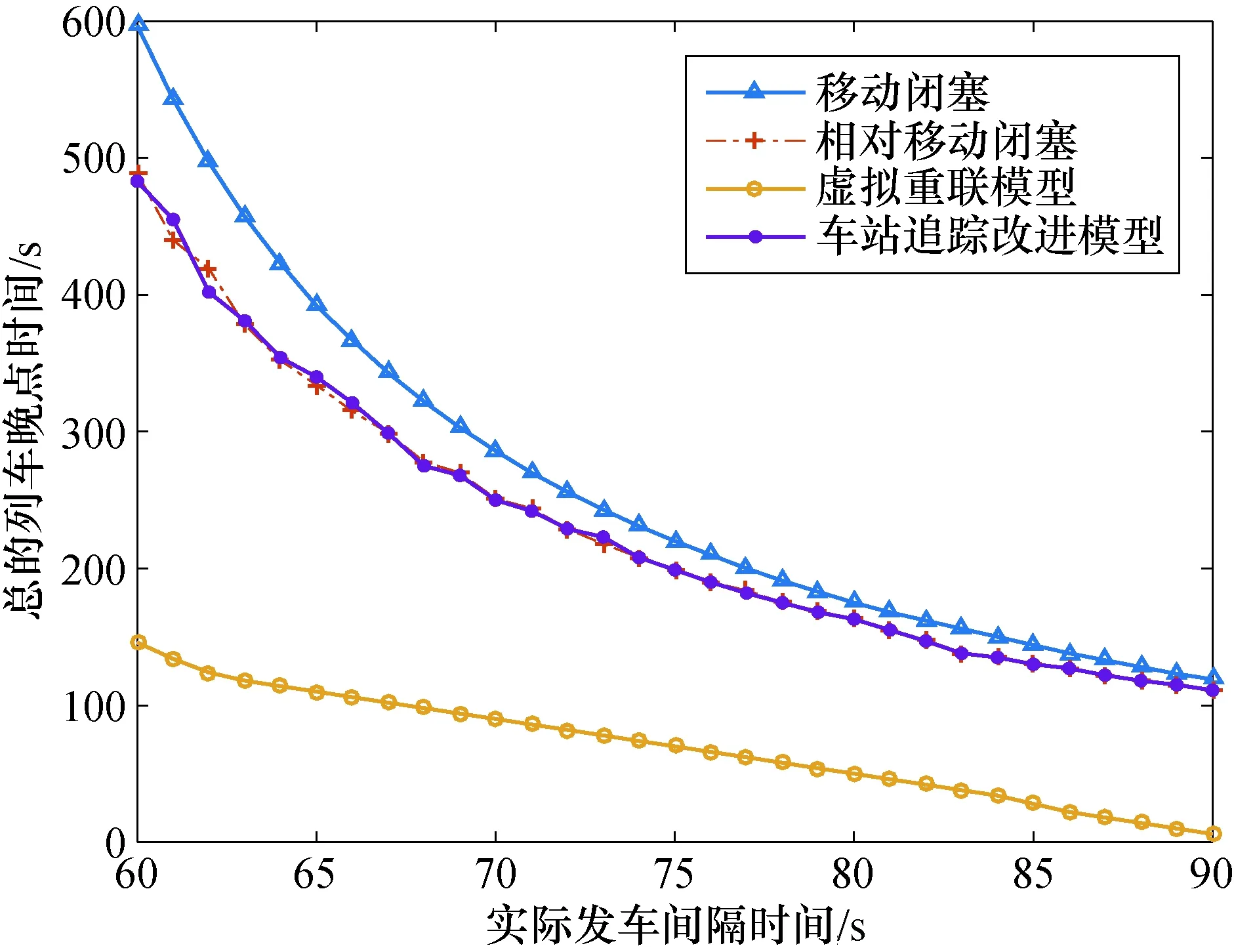
当vn 上述规则中,vn,xn为列车n的速度和位移;vc是系统根据不同的追踪方式应用不同的安全制动模型给出的推荐速度,为0~vmax之间的整数.vc的取值规则如下: 当使用移动闭塞追踪时, 当使用相对移动闭塞追踪时, 其中:s为当前列车与前车的距离;vl为前车当前速度. 模型采用的是开放边界条件.边界定义如下:1)系统每刷新Ti(列车发车间隔)次后,即在初始位置x=0处产生一列速度v=vmax的列车,该车根据系统选用不同的闭塞制式方式,生成不同速度推荐曲线,之后和自身速度对比判断工况运行.系统会保存每列列车在运行时的速度信息和位置信息.2)若列车的位移大于系统规定的长度,则认为该车驶离系统.为了使模拟结果和真实情况对比,规定元胞自动机模型中的系统刷新时间间隔为1 s,一个元胞的长度对应为1 m.列车的最大允许速度都设为20 m/s即72 km/h.系统的仿真流程图如图8所示. 图8 仿真流程图Fig.8 Simulation flow chart 3.2.2 动态性能衡量 系统的仿真场景和仿真参数设置如下:LT=140 m;L=2 000 m;系统总演变时间2 000 s;列车加速度、减速度均为1 m/s2;最大运行速度vmax=72 km/h;安全间隔LS=15 m;系统在中央1 000 m的位置处设立一个车站,车站内车头的停站点位置为1 000 m.特别的,本文中仿真的场景为仅在端点车站设置存车线以及折返线(或到发场),区间中转车站上、下方向各保留一条站线且与区间正线之间实现无道岔连接,所以,在车站不存在“车站到发间隔”[10]. 图9是移动闭塞条件下,头车在车站产生初始延误时,后续追踪列车的速度距离曲线图(列车的发车间隔和最小追踪间隔均为58 s).图9中可以看出,当头车没有初始延误时,后续追踪列车不受头车影响,均匀减速停车,到达车站后又匀加速驶离车站.但是当头车产生延误后,追踪列车就会偏离计划的速度距离曲线,头车延误的时间越长,则追踪列车偏离计划的速度距离曲线越远,甚至会出现停在车站外等候前行列车出站,这与实际情况符合. 图9 头车延误下追踪列车速度距离曲线Fig.9 Speed profile with platform delay under moving block 为了评价不同追踪模式下,初始延迟在不同系统的延迟传播情况,因初始延迟而导致的延误列车数目在仿真时被计算出来.图10是头车初始延迟为120 s的情况下,不同运营发车间隔与列车延误数目的关系图. 图10 不同追踪模式下运营发车间隔时间与列车延误数目关系Fig.10 Effect of service headway on number of perturbed trains with various tracking models 从图10中可以看出,适当增加发车间隔时间的大小可以有效减小因头车产生初始延误而造成的后续列车延误的数量.在实际发车间隔时间一定的前提下,大多数情况下虚拟重联模型和车站追踪改进模型条件下,延误列车的数目和移动闭塞相比,有一定程度的降低;车站追踪改进模型的延误数量和相对移动闭塞的延误数量基本保持一致;虚拟重联模型受到干扰的延误列车数量最少. 为了量化研究系统的恢复能力,系统总延误时间被定义为所有列车经历延误时间的总和[11] (6) 式中:Dt为系统内所有列车因初始延误产生的延误时间,s;N为系统内所有因初始延误产生延误的列车数目;Di第i列列车所经历的延误时间,s. Dt直接表示了所有列车在系统中经历特定扰动时的整体扰动程度,Dt越小说明系统在受到干扰后恢复到正常运营的速度越快.图11是不同的运营发车间隔时间与总延误时间的关系图.由图11中可以看出,从系统总延误时间的角度量化恢复能力,虚拟重联模型的后续所有列车延误恢复能力是最强的;仅在车站区域采用相对移动闭塞的车站追踪改进模型的延误恢复能力与整段线路都采用相对移动闭塞的延误恢复能力非常接近,在部分发车间隔时间下,甚至会超过相对移动闭塞的延误恢复能力;移动闭塞的延误恢复能力在四者中是最弱的. 图11 不同追踪模式下运营发车间隔时间与列车总延误时间关系Fig.11 Effect of service headway on total delay with various tracking models 虚拟重联技术是一种控制列车以编队方式在轨道上追踪运行的技术.该技术利用车-车通信协调各个列车运行过程,实现“空间维度安全、时间维度更近”的运行,从而提高城市轨道交通运营的灵活性,适应变化的交通需求和提升线路的通过能力. 1)对虚拟重联技术需要的安全制动模型进行探讨,介绍了一种改进安全制动模型的方法. 2)针对车站瓶颈区域提出了一种基于虚拟重联追踪间隔模型:即两列列车组合为“一列虚拟重联列车组”,追踪列车与头车之间采用相对移动闭塞行驶,头车与追踪列车组成的列车组又与前方的列车组采用移动闭塞行驶;进而提出了一种改进的车站追踪改进模型:仅在车站区域采用相对移动闭塞追踪,在区间采用移动闭塞追踪. 3)通过Matlab建立4种条件下列车运行仿真系统,数值计算和仿真分析结果表明:车站追踪改进模型与相对移动闭塞通过能力相当,虚拟重联模型通过能力最大;系统受到初始延误后,虚拟重联模型的延误恢复能力最强. 因此,在车站站台存在较大空间的前提下,针对车站区域进行虚拟重联技术的设计是一种提升线路整体通过能力的有效和可行方法,而在车站站台空间有限的条件下,采用车站追踪改进模型可以进一步提升线路通过能力.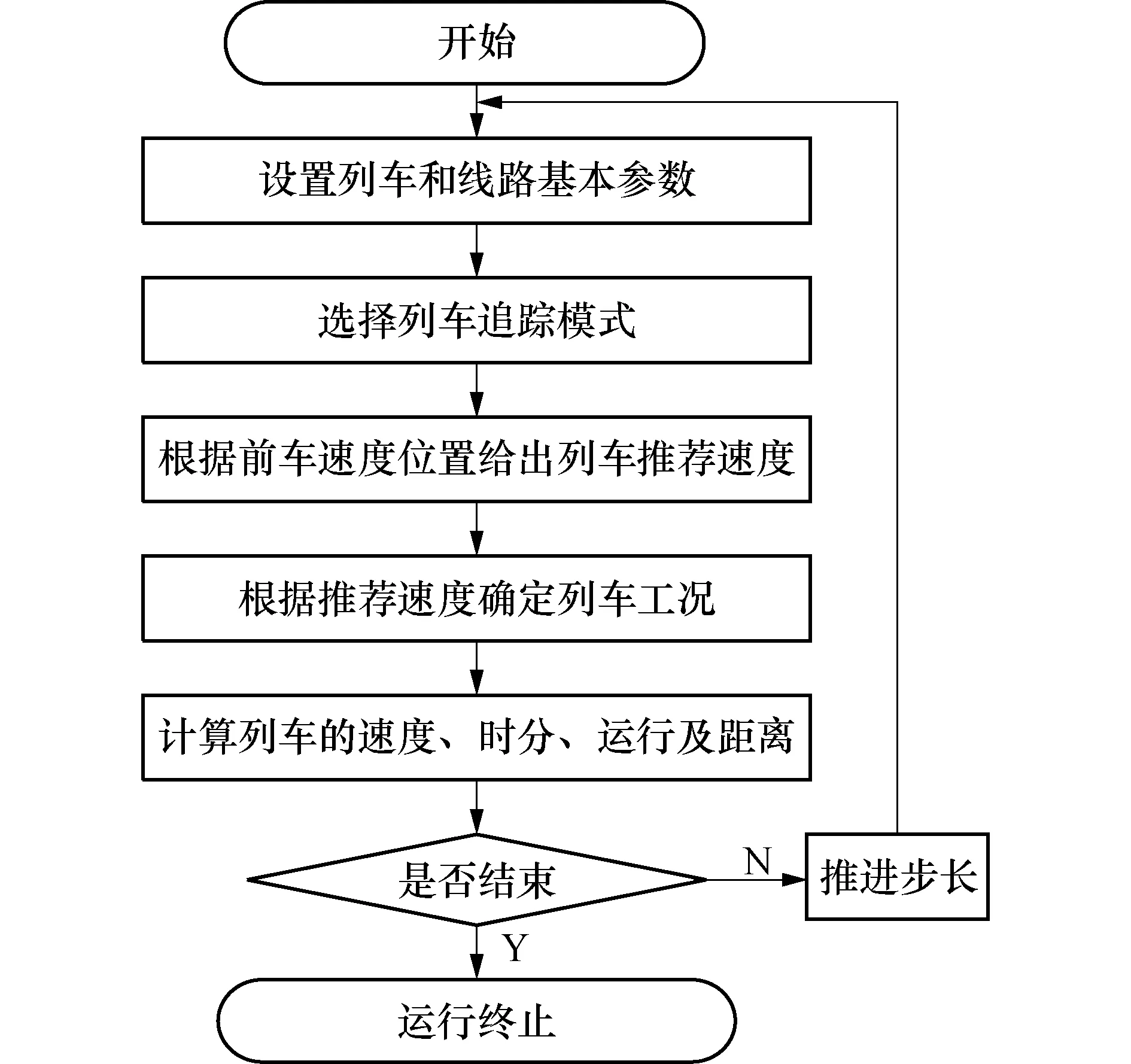

4 结论
