光电二极管的地球反照光校正及卫星姿态估计

褚理想， 樊巧云

(北京航空航天大学仪器科学与光电工程学院, 北京 100083)

姿态估计是卫星上最重要的测量之一。目前常用的姿态传感器有太阳敏感器、地磁、星敏感器、地球敏感器和GPS等，这些传感器有其各自的优点和使用限制。卫星上常装配多种敏感器，采用多种方案相互备份和补充，从而保证测量的可靠性和鲁棒性。光电二极管[1]是一种成本低廉、体积更小的感光传感器，根据其输出电压可以感测太阳矢量方向，可以作为低精度的太阳敏感器。

太阳敏感器与地球敏感器结合[2-3]，可以确定卫星三轴姿态。然而基于光电二极管的太阳敏感器，其输出的电压是太阳光和地球反照光等杂光辐照的叠加，如果忽略地球反照光的影响，直接将测量电压转换为太阳矢量，会导致转换结果存在较大误差，进而影响姿态估计的精度。为此需要考虑地球反照光，建立精确的光电二极管量测模型，才能实现高精度的卫星姿态估计。

文献[4]提出了地球反照光的数学模型及其计算方法，该方法需要实时的球面积分运算，计算较为复杂。文献[5-8]对其进行了简化。文献[5]假设地球表面的反照率仅与地球纬度有关，与地球经度无关，建立地球反照光的查找表并将其拟合成曲面，在已知卫星姿态和卫星轨道位置的情况下可以快速计算地球反照光影响。这种方法前期计算较为复杂且仅适用于单一轨道。文献[6]采用随机实验的方法得到地球反照光统计特性，然后根据统计的均值和方差补偿太阳矢量模型，这种方法对太阳矢量的动态范围有很大限制。文献[7-8]假设地球反照光为与卫星天底方向反向平行的单一矢量，简化地球反照光的计算，但仍存在计算复杂和精度较低的问题。

本文结合地球反照光模型，提出光电二极管动态偏置混合高斯噪声的量测模型，并应用滑窗估计和随机权重策略动态更新地球反照光偏置和噪声方差。在权重更新过程中，引入Huber影响函数处理量测残差的异常值，从而提高了算法鲁棒性和参数估计精度。同时，针对每个光电二极管的地球反照光分布不一，采用多比例因子分别估计每个光电二极管的地球反照光影响。基于本文建立的地球反照光校正的光电二极管太阳敏感器量测模型，结合地球敏感器和陀螺等传感器，采用无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法[9]实现了卫星的高精度姿态估计。

1 地球反照光校正的光电二极管量测模型

1.1 光电二极管工作原理

光电二极管的输出电压和太阳矢量与光电二极管敏感轴夹角的余弦成正比，根据电压输出，可以感测太阳方位。光电二极管常安装于卫星表面，易受周围地球反照光等杂光的干扰。图1为地球反照光几何示意图，照射在积分区域(太阳照射与卫星可视方位区域交集)的太阳光，经地球表面漫反射后，共同作用于卫星方向。地球反照光的计算不仅与地球表面的反照率有关，还和太阳、卫星、地球相对位置有关，此外，地球反照光还与卫星本身的姿态有关。因此地球反照光的分布函数较为复杂，其计算较为繁琐。

地球反照光的影响较大，可达到直射太阳光总量的20%～30%，不能简单地忽略其影响。考虑地球反照光的影响，单个光电二极管的输出电压V可以表示为[10]

V=Vd+Va+vV

(1)

(2)

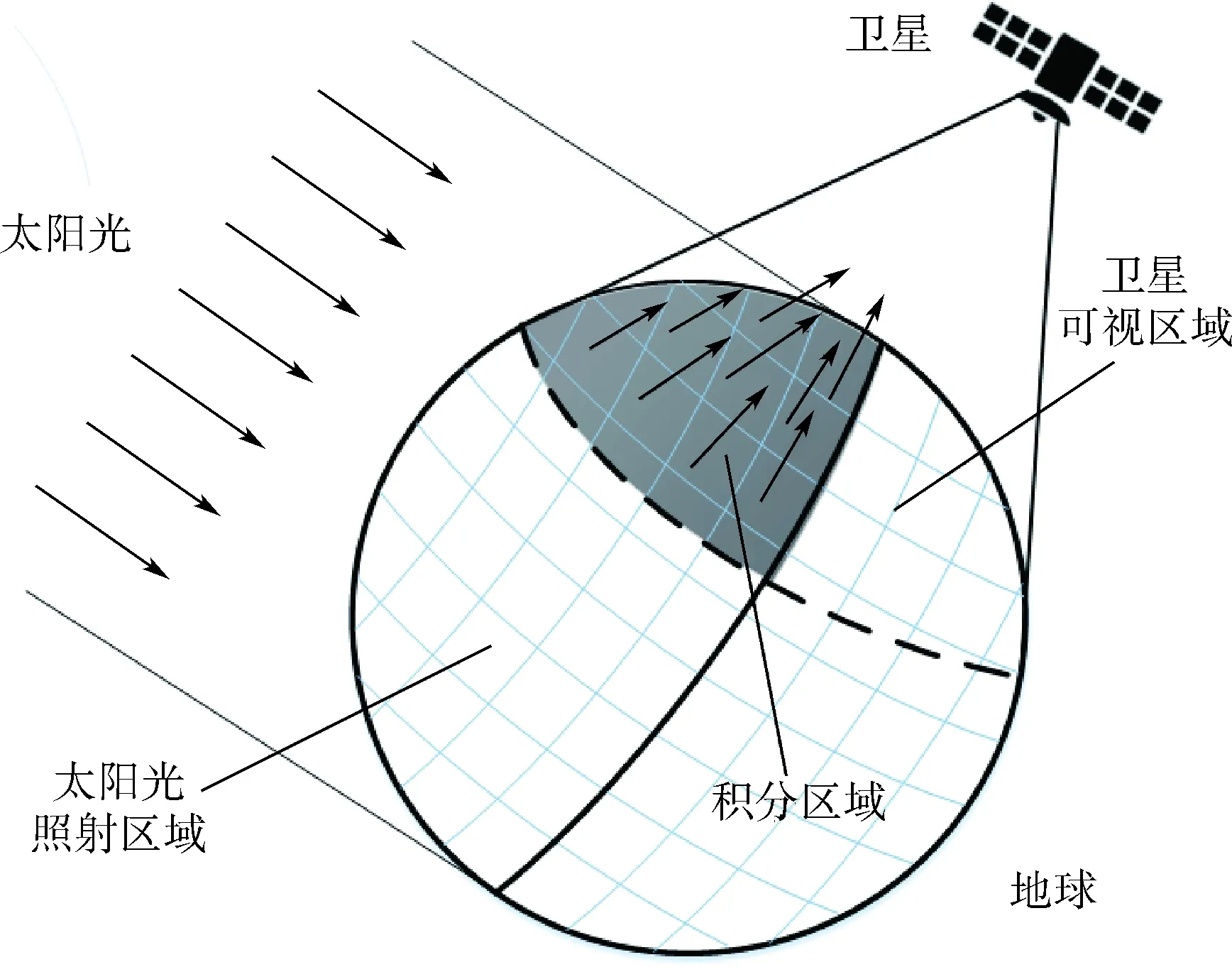
图1 地球反照光几何示意图Fig.1 Geometric sketch of the earth’s albedo

Va=

(3)

式中：Vd为太阳照射分量；Va为地球反照光分量；vV为模型误差的零均值高斯白噪声；n=[cosφcosθcosφsinθsinφ]T为光电二极管敏感轴的单位矢量方向，可由安装高度角φ和方位角θ表示；sb是太阳矢量在本体坐标系下的表示，可由在惯性坐标下太阳矢量经姿态矩阵变换得到；ψ为光电二极管半视场角；A为地球表面卫星可视区域和太阳照射的交集区域；α为地球表面dA的反照率；nA为地球表面面元dA的法向单位矢量；s⊕为地球到太阳的矢量方向；rAB为地球表面面元dA到卫星的矢量方向；B表示卫星当前轨道位置；S表示在地球阴影区的轨道。

1.2 地球反照光校正

式(3)中地球反照光分量Va计算需要球面积分，运算复杂，难以在实际中得到应用。本文将地球反照光设成一动态偏置项，补偿在光电二极管的量测模型中，同时将动态偏置估计的误差和光电二极管本身量测的误差统一为混合高斯模型，建立光电二极管的动态偏置混合高斯量测模型：

Vk=Vd,k+rk+vk

(4)

式中：下标k表示采样时间序列；rk为地球反照光动态偏置；vk为非高斯噪声，可用式(5)表示:

p(vk)=(1-ε)pN(vk)+εqN(vk)

(5)

其中：pN(vk)为已知的均值为0、方差为R1,k的高斯噪声概率密度函数；qN(vk)为未知的均值为0、方差为R2,k的污染噪声概率密度函数；参数ε∈(0,1)为污染系数，用来控制污染噪声的强弱，本文取ε=0.05；p(vk)为整体量测噪声vk的概率密度函数，其方差为Rk，满足Rk=(1-ε)R1,k+εR2,k。

单个光电二极管仅能测量一个太阳矢量分量，至少需要有3个有效的光电二极管量测值才能求取完整的太阳矢量。对于多个光电二极管的量测模型，可以表示为

(6)

矢量表示形式为

Vk=Vd,k+rk+vk=Hsb,k+rk+vk

(7)

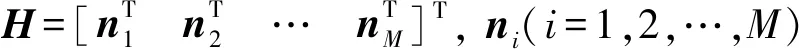
2 模型参数的在线估计和更新方法

式(7)中地球反照光校正的光电二极管量测模型的地球反照光偏置项rk和噪声方差Rk是未知的，需要在卫星姿态估计过程中在线估计并动态更新。本文采用滑窗估计和随机权重策略动态更新模型参数，如图2所示，假设模型参数在窗口采样时间序列k-1,k-2,…,k-N范围内不变，对于历史数据计算的模型参数赋予不同的权重，获取当前时刻模型估计的参数。由式(7)，结合滑窗估计和随机权重算法，此时可以得到动态偏置和噪声方差的估计公式分别为

(8)

(9)

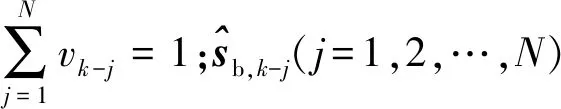
随着量测噪声的统计变化，量测残差向量ek-j将存在偏置，它的幅值将会增加[11]，可以选用量测残差的模值作为权重，如式(10)和式(11)所示：

wj∝|ek-j|j=1,2,…,N

(10)

(11)

然而光电二极管噪声分布较为复杂，当出现 残差较大的异常值时，直接采用残差向量作为模值会引起权重分配不合理，进而导致偏差和方差估计产生较大误差。基于Huber影响函数的鲁棒技术可以有效地处理非高斯噪声的情况，其更改了后验噪声方差矩阵，降低了对异常值的灵敏度。因此，本文引入Huber影响函数处理量测残差的异常值，其表达式如下：

图2 滑窗估计和随机权重算法示意图Fig.2 Schematic diagram of sliding window estimation and random weighting algorithm

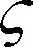
(12)

(13)

式中：引入Tk使ηk满足关于概率密度对称和边缘概率密度条件[12]。ψ(·)是Huber函数，其表达式为

(14)

其中:sgn(·)是符号函数；kε的取值和污染系数ε有关。

另外，考虑到每个光电二极管的地球反照光的分布情况不同，当所有的光电二极管都采用统一的权重系数会降低对地球反照光的跟踪特性，因此本文采用多重比例因子分别估计地球反照光对每个光电二极管的影响，此时可得

(15)

(16)

式中：diag(·)表示将一个向量转换为对角矩阵。

3 基于UKF的卫星姿态估计

3.1 姿态估计状态方程

卫星姿态运动学[13]可以用四元数表示为

(17)

(18)

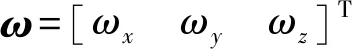
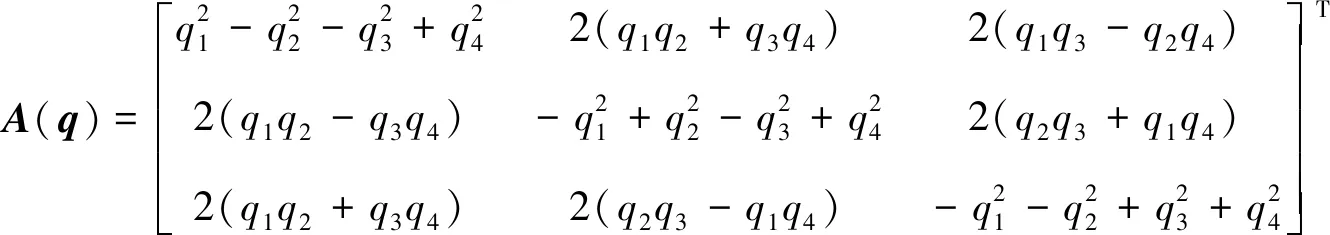
(19)

陀螺常用的数学模型为[15]

(20)

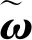
(21)

其中：δ(t-τ)为Dirac delta函数。

此时可以建立卫星姿态估计的连续状态方程为

(22)

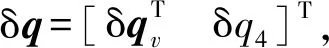
δp=f[δqv/(a+δq4)]

(23)

式中：a为0到1区间的参数；f为放大因子。a=0 和f=1表示的是Gibbs向量，a=1和f=1表示的修正罗德里格斯向量。从δp到δq的逆变换为

(24)

δqv=f-1(a+δq4)δp

(25)

3.2 姿态估计量测方程

本文采用光电二极管和地球敏感器两种姿态传感器，需要将其测量值融入到量测方程中。光电二极管的量测方程另一种表达形式为

Vk=Hsb+rk+vk=HA(q)sref+rk+vk

(26)

式中：sref为太阳矢量在惯性下的表示，可以查找星历表获得。

地球敏感器测量天底方向，其量测模型可以表示为

bk=A(q)rearth+εk

(27)

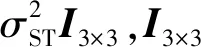
结合2个传感器测量模型可得量测方程：

(28)

3.3 UKF算法实现

当已知状态更新的状态方程模型，且建立了状态和量测方程的噪声和误差统计模型，卡尔曼滤波方法采用递推的方式，从量测信息中实时提取出被估计量信息并存储在估计值中[17]。UKF是对线性卡尔曼滤波的改进，其不需要对状态方程和量测方程线性化，常用于姿态估计等非线性滤波算法中。UKF通过sigma点捕获系统真实的均值和方差，其精度可以达到泰勒展开式三阶近似。

定义离散系统的非线性状态方程和量测方程为

(29)

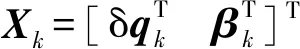
(30)

(31)

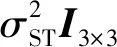
4 仿真校验

4.1 仿真条件

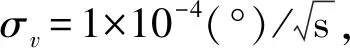
n1=[cos(10°)cos(72°) cos(10°)sin(72°)

sin(10°)]T

n2=[cos(10°)cos(107°) cos(10°)sin(107°)

sin(10°)]T

n3=[cos(-20°)cos(90°) cos(-20°)sin(90°)

sin(-20°)]T

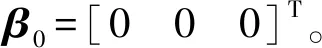
图3为3个光电二极管的理想电压和量测电压的对比图，地球反照光影响为量测电压与理想电压的差值。由图中可以看出，对于同一个光电二极管，在轨道的不同时段,地球反照光与太阳直射光的比值不同,比值大约为0～25%。对于不同光电二极管，每个光电二极管的地球反照光分布情况不同。此外，在卫星刚出背光面和刚入背光面时，理想光电二极管和实际光电二极管的电压相差不大，地球反照光较弱，可以选择卫星刚出背光面时刻作为太阳矢量估计或者姿态估计的初始时刻。

4.2 仿真结果

为了量化仿真结果，选取三轴欧拉角的模值作为评判指标：

(32)

式中：θk、φk和ψk分别为横滚角、俯仰角和偏航角。为了保证结果的可靠性，参数使用蒙特卡罗仿真50次。基于本文建立的地球反照光校正的光电二极管太阳敏感器量测模型，结合地球敏感器和陀螺等传感器，采用UKF算法进行卫星姿态估计。

图4对比了固定权重(如均值)、量测残差模值、量测残差经Huber影响函数处理后的模值、本文方法等4种权重选取策略的效果。从整体来看，在初始三轴卫星姿态1.5°左右时，采用本文 建立的地球反照光校正模型和UKF算法，三轴姿态精度可以很快的收敛到0.5°甚至更高精度，验证了本文简化地球反照光模型具有一定的可行性。比较不同权重选择策略，可以看出采用本文方法精度较高，三轴姿态精度可以达到0.2°～0.3°。

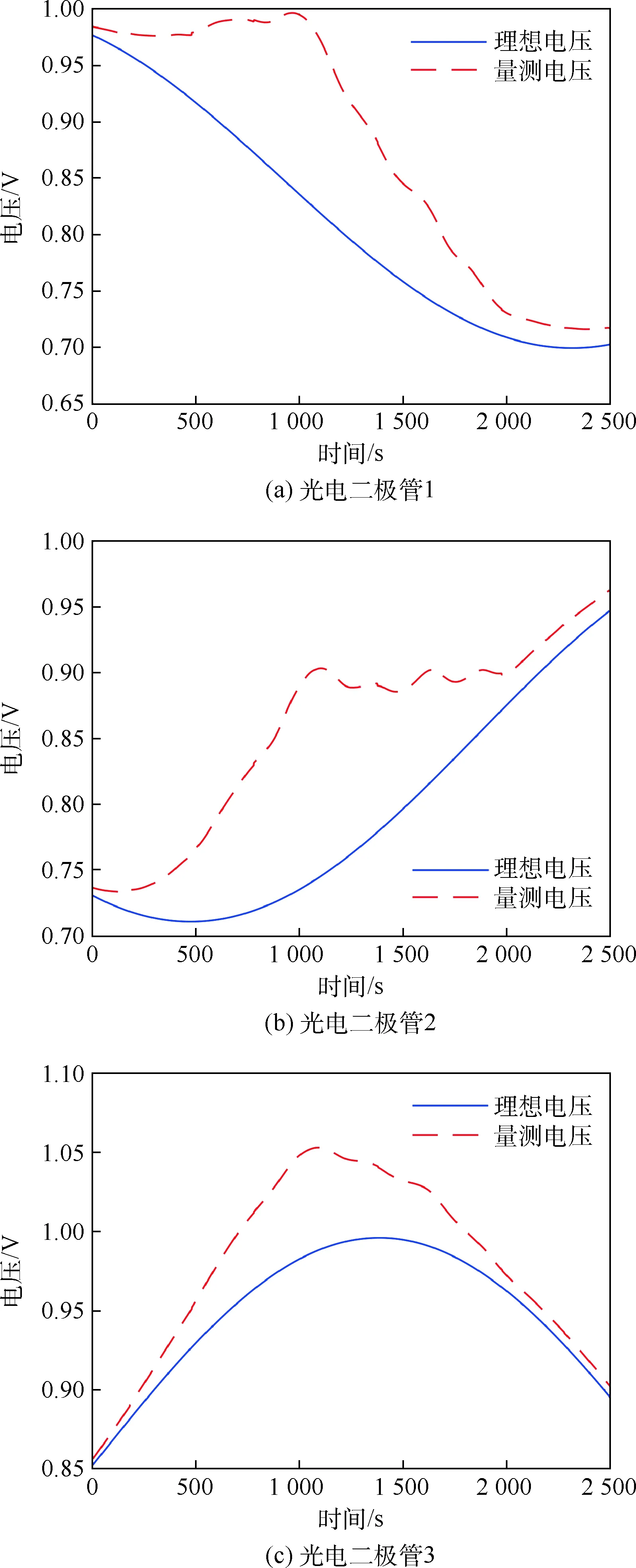
图3 光电二极管1、2和3的理想电压与量测电压对比Fig.3 Comparison of ideal voltage and measured voltage for photodiode 1，2 and 3

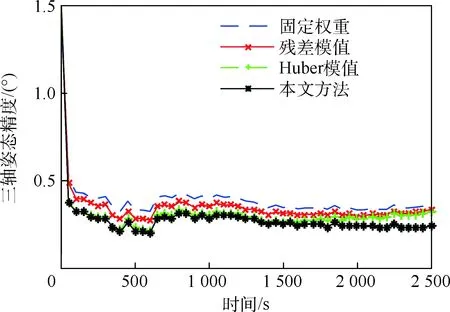
图4 卫星三轴姿态估计误差对比Fig.4 Comparison of satellite three-axis attitude estimation error

此外，还可以以地球反照光建模的动态偏置电压估计精度作为评价标准，地球反照光估计精度越高，光电二极管测量的太阳矢量精度就越高，进而姿态的估计精度越高。单个光电二极管的偏置估计误差可以通过多次蒙特卡罗方法求均值获得。表1为光电二极管偏置估计误差均方根(RMS)结果，可以看出，本文权重选取策略可以有效提高偏置估计精度。图5为3个光电二极管的偏置估计误差。从图5(b)可以明显看出,偏置估计的误差随时间推移而明显减小，偏置估计的精度越来越高。

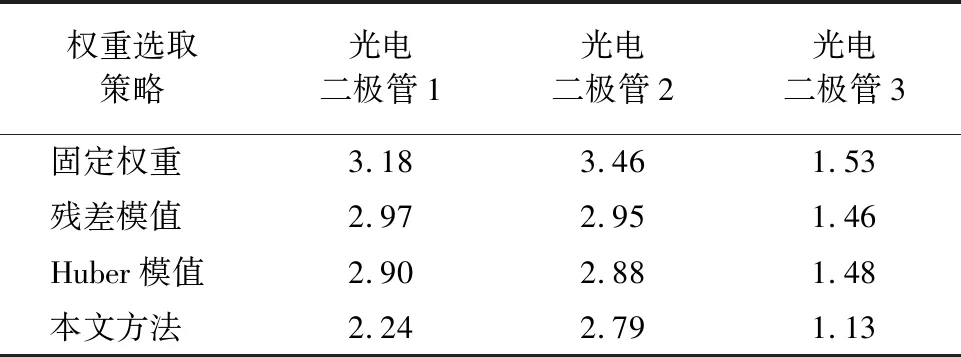
表1 光电二极管偏置估计误差RMSTable 1 RMS of photodiode bias estimation error mV

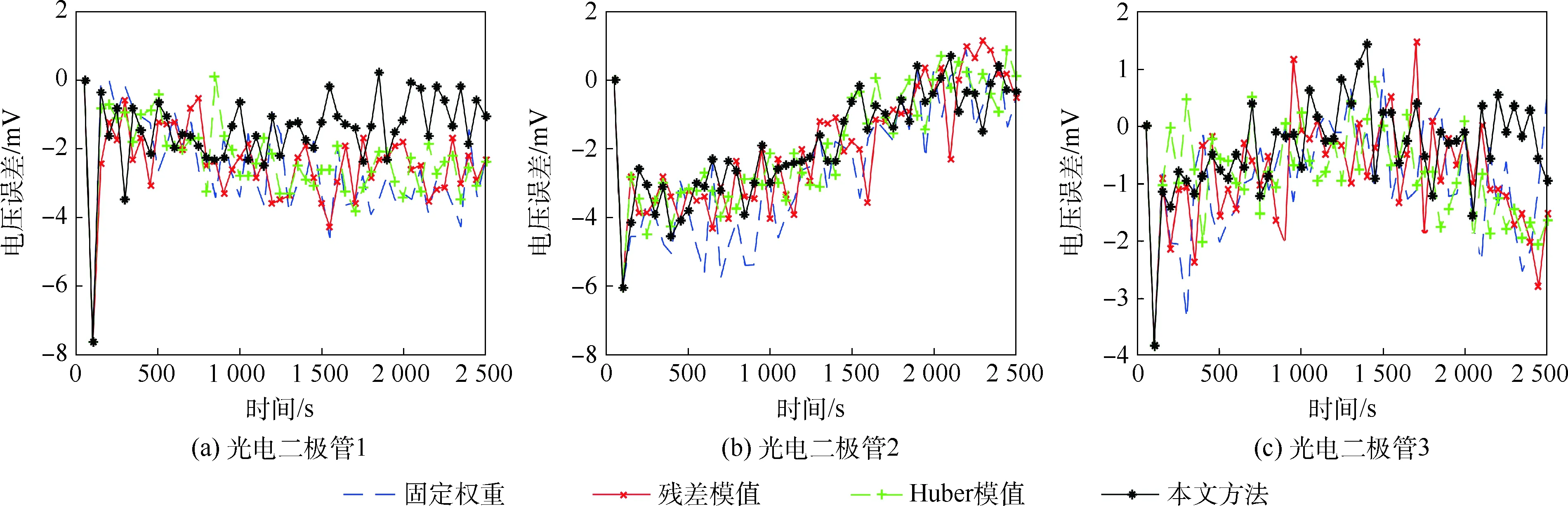
图5 光电二极管1、2和3的偏置估计误差Fig.5 Bias estimation errors of photodiode 1,2 and 3

5 结 论

针对地球反照光的影响，本文建立了光电二极管动态偏置混合高斯量测模型，简单有效，通过对地球反照光的准确估计，提高了光电二极管对太阳矢量的测量精度。实验表明：

1) 应用地球反照光校正的光电二极管和地球敏感器组合定姿，可以消弱地球地球反照光的干扰，快速提高三轴姿态精度，精度可以达到0.2°～0.3°。

2) 在应用滑窗估计和随机权重估计量测模型参数过程中，采用多比例因子和Huber影响函数的权重处理方法，可以有效提高地球反照光动态偏置电压的估计精度。

本文提出的地球反照光校正方法，可以推广应用于光电二极管与其他姿态传感器(如地磁)的组合定姿。