一种起落架载荷谱相似性判别方法

2019-05-05颜灿林贺小帆李玉海

北京航空航天大学学报 2019年4期

颜灿林，贺小帆, 李玉海

(北京航空航天大学航空科学与工程学院，北京 100083)

飞机结构在设计研制阶段，需要进行基准谱下的寿命实验，确定机群的基准寿命。飞机实际载荷历程往往与规定的使用情况有差异，而机群的基准使用寿命是针对规定使用方法给出的，不能反映单架飞机损伤情况。为保证飞机结构的安全性与经济性，现役先进飞机普遍进行单机寿命监控[1]。起落架结构作为飞机结构重要的飞行安全件，直接影响着飞机结构的安全。据统计，由于起落架故障引发的事故占飞机总事故数量的40%以上，其中由于起落架关键部位疲劳破坏导致的起落架故障所占比例高达50%[2]。由于起落架主要承力部件为单通道传力结构，载荷环境恶劣，材料大多采用高强度合金钢，缺口敏感，疲劳裂纹扩展迅速，结构复杂，造价昂贵，如何在保障安全的情况下充分发挥寿命潜力是一个重要问题。因此，对起落架结构进行寿命监控，实时监控关键部位的疲劳状态尤为重要。

单机寿命监控主要包括关键部位载荷数据采集、编制单机谱、单机谱损伤分析、寿命管理4个部分[3]，载荷谱的损伤分析是其中重要一环。由于起落架及相关结构主要承受地面载荷的作用，着陆撞击过程中拉-压载荷交互作用，存在明显高低载荷非线性耦合，给载荷谱损伤分析带来很大困难[4-6]。针对起落架单机谱的损伤计算通常有2种途径。①通过实验与有限元计算分析将起落架名义应力对应的载荷状态转化为关键部位的局部应力-应变状态，并采用合理的损伤计算方法评估关键部位的损伤。这种方法应用复杂，需要进行大量迭代，即使得到真实的局部应力-应变状态，目前也并不存在广泛适用的累积损伤理论[7]。②直接通过起落架结构的名义应力谱，采用基于等损伤应力折算公式——SWT公式[8]计算名义应力谱的当量损伤，结合基准谱下的实验寿命结果，对比基准谱与单机谱的当量损伤得到单机谱的真实损伤。这种方法的优点在于应用简单，目前广泛应用于以过载因子-超越数为特征的飞行谱损伤计算[9-11]，飞行谱以科目为单元，极少存在高载-负载耦合的情况，然而起落架谱存在明显高载-负载交互作用，使用当量损伤法不能准确计算单机谱损伤。因此，起落架谱损伤分析一直是起落架寿命监控中的难题，如何提高损伤计算精度是问题的关键。为了解决载荷顺序效应造成损伤计算困难，通常的做法是选取合适的损伤计算方法及非线性累积损伤理论。然而大量损伤累积理论[7]表明对这类每次起落均会承受拉-压载荷冲击的起落架载荷谱而言，并没有损伤累积理论可以准确计算损伤。

大量实验与经验表明对于构成形状相似的2个载荷谱，采用相同的损伤计算方法可以得到较为准确的损伤比值。因此本文考虑根据基准谱下已有的实验结果，对于使用过程中单机谱预先施加判别条件，判断单机谱与基准谱的相似度，进而分析损伤计算方法的适用性。目前关于载荷谱的相似性的研究较少，在汽车行业中针对程序块谱提出载荷谱形状因子(Spectrum Shape Factor，SSF)[12-13]，可以用来评估载荷谱的相似性，但该方法本质上通过谱的损伤来确定谱的形状因子，仍然避免不了损伤计算。姚卫星等[14]提出基于Bhattacharyya距离(简称B距离)综合考虑寿命均值与分散性衡量原谱与等效谱寿命相似程度，本质上仍然是通过损伤分析得到的结果。本文基于时间序列分析中动态弯曲方法[15]，从载荷谱形状的角度出发判别载荷谱的相似性，得到单机谱与基准谱的相似距离，并通过当量损伤方法的计算误差给予验证。

1 当量损伤计算

本节简要介绍当量损伤方法[9]的流程。在材料性能参数未知的情况下，当量损伤方法采用基于SWT公式[8]和线性累积损伤理论的方法计算载荷谱损伤。采用指定应力比下S-N曲线(式(1))表征结构的疲劳性能。

SmN=C

(1)

式中：S为结构名义应力;N为名义应力S下结构寿命;S-N曲线参数m的取值与材料、结构特性以及载荷情况相关，在未获取材料S-N曲线前可统一取m=4;C为材料常数。线性疲劳累积损伤理论指出，在循环载荷作用下，疲劳损伤是线性累加的，各个应力之间相互独立和互不相关，当累积损伤达到某一数值时，试件或者构件就发生疲劳破坏。按Miner线性损伤累积损伤理论，单个循环损伤可按式(2)计算：

(2)

式中：Ci和m为第i次应力循环下的S-N曲线参数；Ni为在当前应力水平Si下的寿命。累积各次循环损伤得到载荷谱真实损伤计算式为

(3)

式中：n为各级载荷循环数量之和；di为第i个循环对结构造成的疲劳损伤。Ci受循环应力比的影响。为了考虑载荷谱中的应力比的影响，SWT公式将所有的载荷循环转换为对称循环(应力比为-1)，其形式为

(4)

式中：Smax与Smin为一次载荷循环的最大值与最小值；R为应力比；S-1为转换为应力比-1的对称循环峰值。每个载荷循环的损伤可以表示为

(5)

其中：C-1为应力比为-1的S-N曲线参数，此值为定值，可以略去。单次循环的当量损伤表示为

(6)

单机谱的当量损伤可以表示为

(7)

在评估单机谱的损伤时，通过分别计算单机谱与基准谱的当量损伤，得到单机谱当量损伤与基准谱当量损伤的比值，结合基准谱下的实验寿命，即可得到单机谱真实损伤值。

(8)

式中：Dreal为单机谱的真实损伤，其临界值为1；Dbase为基准谱的当量损伤；t为基准谱下的全尺寸寿命实验经历的谱块数。

当量损伤计算方法并未考虑载荷顺序效应带来的影响，但是在单机谱与基准谱构成形式相似时，高低载荷的交互作用对损伤计算的影响近似一致，采用该方法计算得到的二者当量损伤的比值应接近于二者真实损伤的比值，而随着单机谱与基准谱差异增大，复杂的交互作用使得损伤计算误差迅速增加，因此需要建立一种起落架载荷谱相似性判别方法，比较各个单机谱与基准谱的相似程度。

2 起落架载荷谱的相似性度量

2.1 起落架载荷谱的相似性

关于随机谱的相似性判别，目前存在的研究较少，通常以载荷-超越数曲线描述飞机结构载荷谱，并通过载荷-超越数曲线相似进而认定2个载荷谱损伤相当，但载荷-超越数曲线是由载荷序列计数得到，丧失了原有的载荷顺序信息。针对Gassner提出的载荷逐级递减的多级程序块谱，Heuler、Klätschke[12]和Facchinetti[13]提出采用载荷谱形状因子[12-13]来判别载荷谱的形状。基于S-N曲线与线性累积损伤理论，SSF定义为

(9)

式中：∑Ni为程序块谱各级载荷循环数之和；∑Ni,eq为程序块谱中各级载荷循环等损伤折算为最大载荷对应循环数之和。该方法用于载荷逐级变化的程序块谱，避免了载荷顺序效应带来的影响，本质上是在损伤计算准确的前提下判别载荷谱与等幅谱的偏离程度。然而由于起落架载荷谱存在高低载荷交互作用，无法准确计算各个循环的损伤，因此无法通过SSF来表征载荷谱的形状。本文仅从载荷谱形状出发，所指的载荷谱的相似性是指两段载荷序列，细节上不完全相同，但形状上具有一定的相似性，即各级载荷出现的顺序，高载出现的位置以及循环数量具有一定的相似性。此外，对于起落架结构所承受的载荷，在一个起落范围内无论飞机执行何种任务，每次起降的动作基本一致，都包含着陆、滑行、刹车、转弯、起飞线试车、牵引等过程，着陆撞击产生的高载荷均匀地分布在地面滑跑、操纵载荷之间，高低载荷的位置相对固定，形式较为单一，每次起落的载荷本身具有一定的相似性。图1为一段典型的起落架载荷序列，纵轴表示单位化后的载荷。

针对起落架载荷谱这一特殊的载荷谱形式，从时域角度出发，比较不同起落架载荷谱的相似程度。疲劳载荷谱本质上是一段时间序列，重要的要素为载荷的大小、出现的顺序、循环次数，重点关注的是谱中最大载荷循环，以及出现的先后顺序，而对载荷点之间的时间间隔予以忽略。将一段载荷序列抽象成为时间轴能够自由伸缩的时间序列，判别起落架载荷谱的相似性的问题转变成判别时间轴伸缩的时间序列的相似性问题。

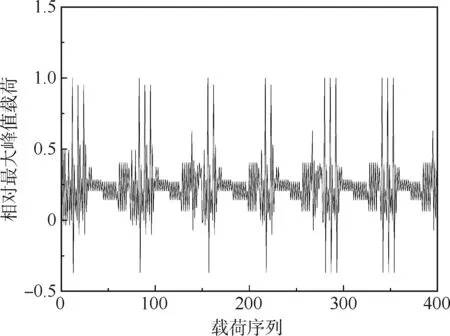
图1 典型起落架载荷谱Fig.1 Typical landing gear load spectrum

2.2 动态时间弯曲

引入动态时间弯曲(DTW)方法度量起落架载荷谱的相似性。DTW距离由Berndt和 Clifford于20世纪90年代引入到时间序列数据挖掘领域[16]，在动作识别[17]、飞行载荷的识别[18]中也有应用，该方法支持时间轴上的伸缩，不要求序列点一一匹配，可以通过求得不同长度序列之间的距离来支持序列对齐匹配，消除欧氏距离只能点对点匹配的缺陷，以最小的代价使得时间轴弯曲，从而使得时间序列点得到一对多的匹配。该方法的示意图见图2，图2(a)为欧氏距离匹配，图2(b)为DTW距离匹配，区别在于DTW在保证点的顺序的情况下，不要求一一对应，寻求两点之间的最小欧氏距离。该方法应用在起落架载荷谱相似度比较时，可以尽量匹配到每个起落内最大峰与最小谷值，而这些点正是对损伤影响较大的部分，理论上该方法可以用于起落架载荷谱的相似性判别。

DTW方法以动态规划为基础，寻找两列时间序列的最短距离。具体做法如下:设有时间序列T1={a1,a2,…,an}，和时间序列T2={b1,b2,…,bm}，an和bm分别表示2段时间序列各采样点数据。将它们按照其时间位置排序，构造m行n列的距离矩阵D，即

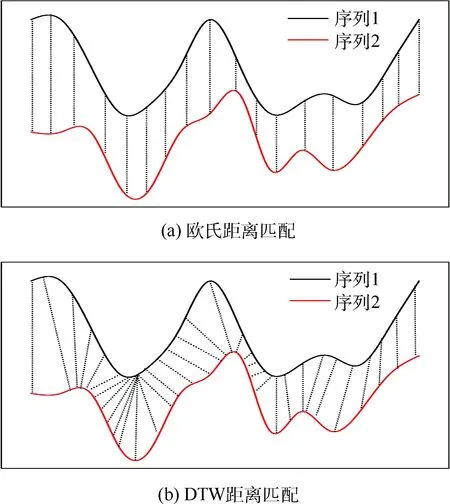
图2 欧氏距离匹配与DTW距离匹配对比Fig.2 Comparison of Euclidean distance matching and dynamic time warping distance matching

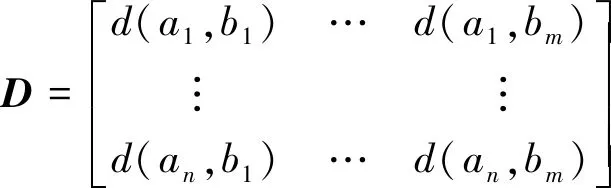
(10)

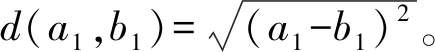
DDTW(T1,T2)=d(a1,b1)+min{Ddtw(T1,rest(T2)),

Ddtw(rest(T1),T2),Ddtw(rest(T1),rest(T2))}

(11)

式中：rest(T1)={a2,a3,…,an}；rest(T2)={b2,b3,…,bm}；Ddtw(T1,rest(T2))表示计算时间序列T1与剔除前一点的时间序列T2的DTW距离。

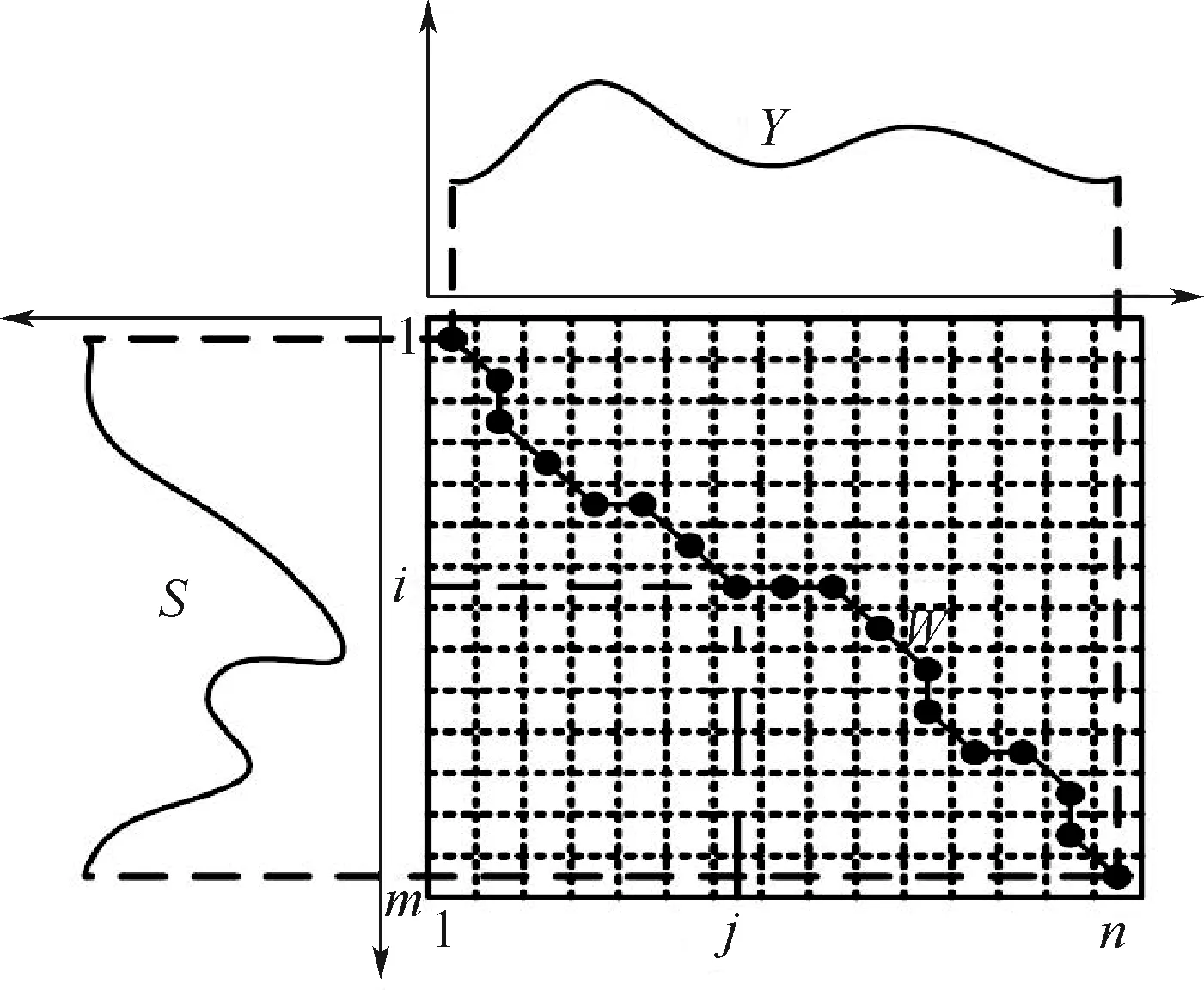
图3 动态弯曲路径示意图[16]Fig.3 Illustration of dynamic warping path[16]

2.3 基于SWT公式的DTW方法

将2.2节的DTW方法应用于起落架载荷谱分析仍然存在一个问题，距离矩阵D中的元素为载荷谱对应点之间的欧氏距离，寻找最短路径的标准也是依据载荷点之间的欧氏距离，该距离仅表征了载荷点之间的绝对距离。然而疲劳损伤不仅与载荷幅值有关，还与均值有关。距离计算方法比较如图4所示，横轴代表载荷序列，纵轴各载荷点应力。采用欧氏距离计算A、B间与B、C间的距离，结果显示二者相等，即A、B间的差异程度与B、C间相同，然而从疲劳载荷谱的角度出发，A、B两点间的平均应力高于B、C间的平均应力，就单个载荷循环而言，将B变为A对载荷谱损伤造成的影响必然大于将C变为B的影响，疲劳载荷谱的相似性分析需要综合考虑载荷点之间的均值与幅值，而欧氏距离显然不能适用。

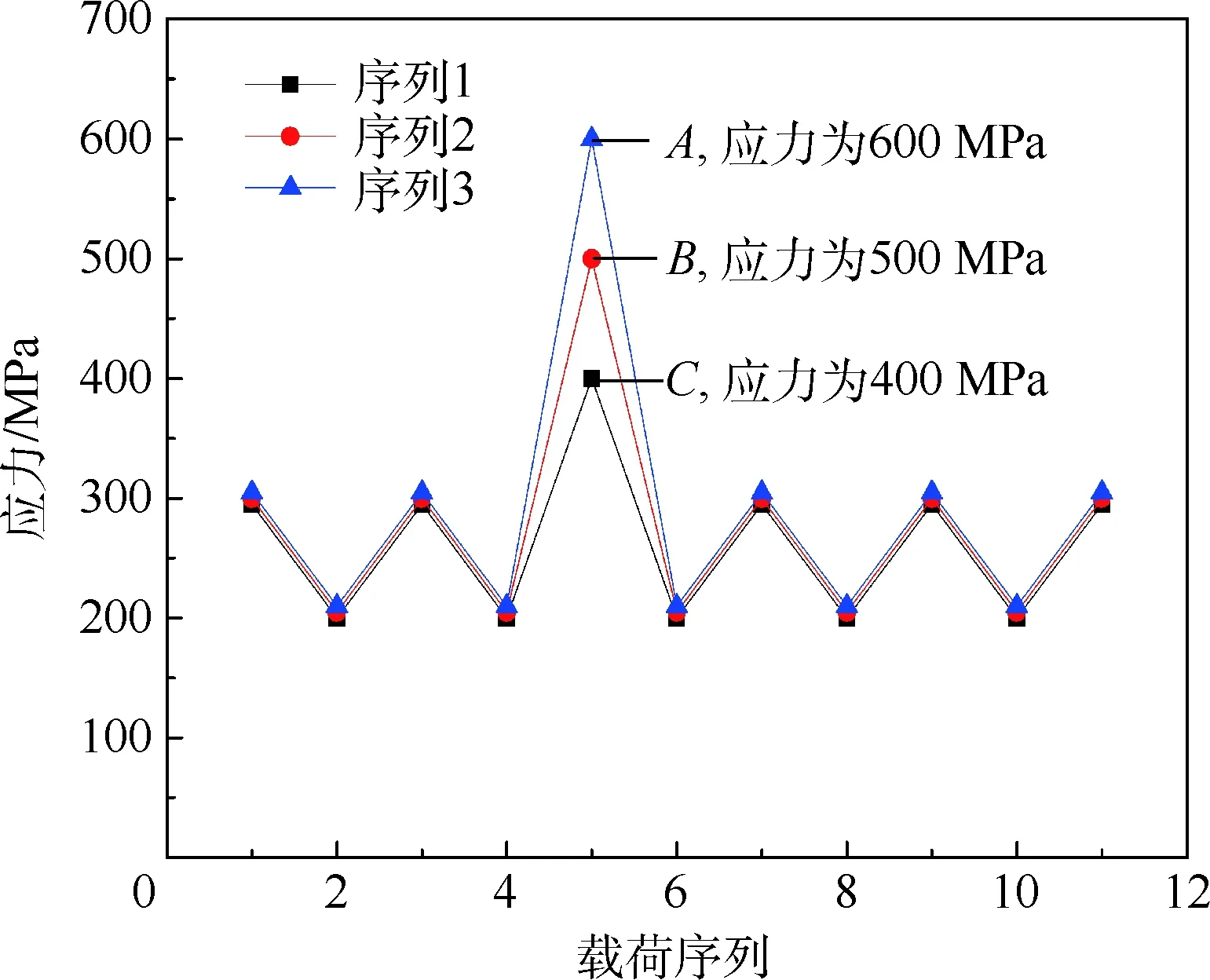
图4 距离计算方法比较Fig.4 Comparison of distance calculation methods

为了使距离矩阵中的元素既能够反映疲劳损伤的特点，又能体现载荷谱的接近程度。参考第1节中提到的SWT公式，该公式将任意一个载荷循环等损伤折算为对称循环，可以综合考虑均值与幅值的影响，将距离矩阵中元素改写为

(12)

式中：c=max{|a|,|b|}，|a|、|b|为a、b两距离测点值的绝对值，a、b为任意距离测点，该公式将2个载荷谱中的对应载荷点假想为一个载荷循环(a,b)，并采用类似于等SWT公式的方法计算得到该循环的等效循环的“峰值”，本文称之为损伤距离。

尽管称之为“距离”，实际上式(2)并不满足传统的距离的定义。良好的距离定义需要满足3个基本条件：

1) 非负性，d(a,b)≥0。

2) 对称性，d(a,b)=d(b,a)。

3) 三角不等式，d(a,b)+d(b,c)≥d(a,c)。

观察式(12)不难发现，条件1)、2)容易满足，条件3)并不满足，式(12)与SWT公式的关系为

(13)

式(13)同时也满足当量损伤的幂函数形式，因此损伤距离公式具有损伤的含义。仍考虑图4中的情况，一个(A,C)载荷循环造成的损伤必然大与(A,B)与(B,C)循环造成的损伤之和，容易得到d(a,b)+d(b,c)≤d(a,c)，不满足三角不等式。这表明虽然将式(12)定义为“损伤距离”，该表达式却并不是真正定义上的距离。

损伤距离可以理解为从疲劳损伤的角度度量两级载荷间的近似程度，若两级载荷的疲劳损伤差别较小，则表示两级载荷更接近，同样以图4中A、B、C3点为例，采用式(12)分别计算图4中A、B间与B、C间的损伤距离，可以得到d(A,B)>d(B,C)，即B、C两点间的载荷更接近，符合疲劳损伤的特点。因此该式(12)综合考虑了载荷幅值与均值的影响，可以反映出两级载荷的近似程度。

3 实验及分析

根据第1节，采用当量损伤计算方法计算载荷谱损伤时，其计算误差会随着基准谱与单机谱的相似程度降低而增加。根据本文所提出的相似性判别方法，进行了实验获取各载荷谱的真实损伤，采用第1节中的当量损伤计算方法进行预测，并分析实验与预测结果的误差。根据第2节提出的相似性判别方法计算得到各载荷谱与基准谱的DTW距离，结论表明损伤预测的精度随DTW距离增加而降低，即DTW方法可以用于起落架载荷谱的相似性度量。

3.1 起落架下陷细节模拟件

试件模拟起落架外筒变截面处，试件材料采用高强度合金钢30CrMnSiNi2A，试件长300 mm，厚7 mm，夹持段宽50 mm，工作段宽30 mm，含有一个半径为10 mm下陷过渡圆角，试件表面粗糙度Ra=1.6，试件尺寸见图5。

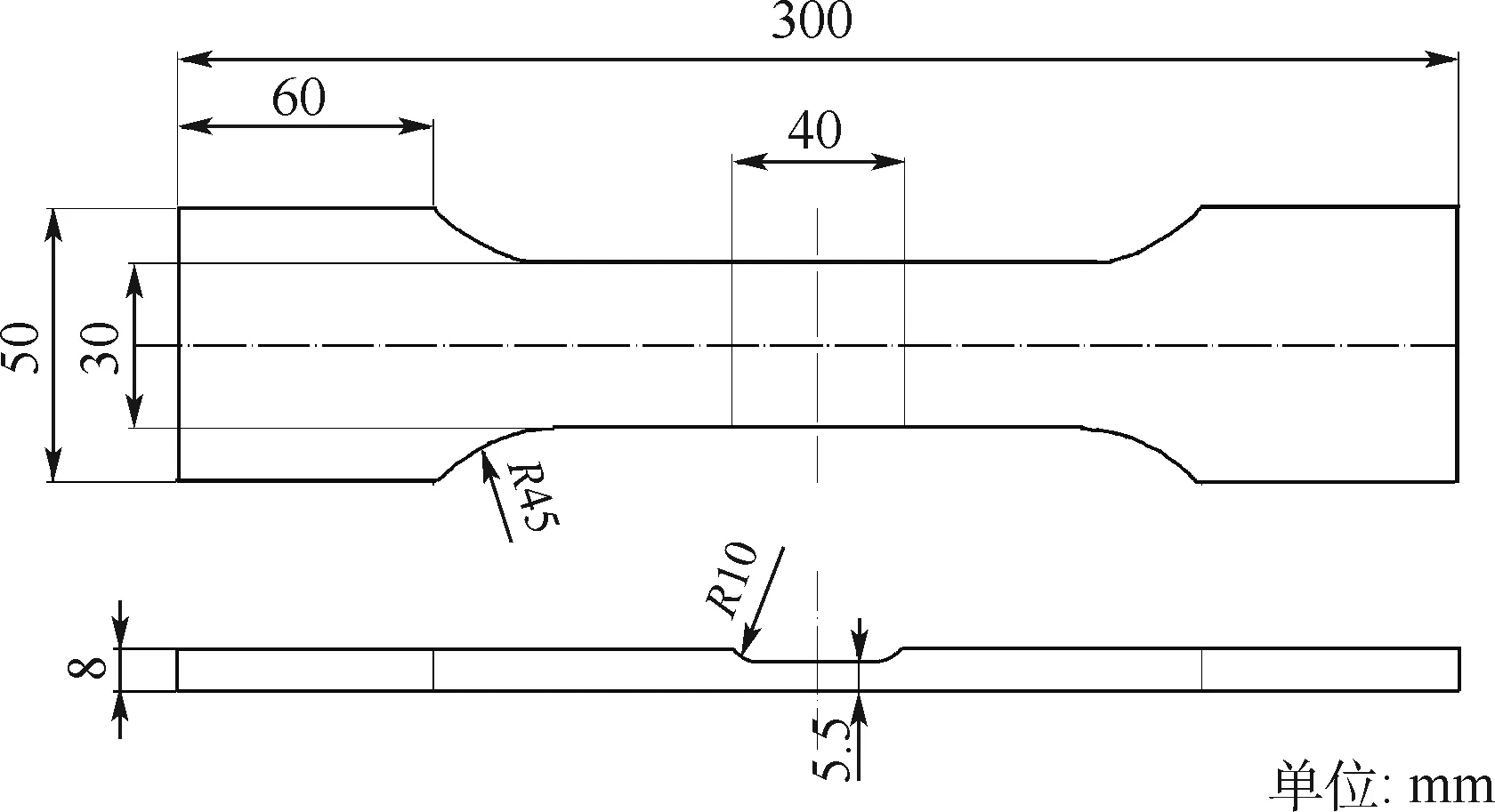
图5 试件几何形状Fig.5 Geometry of specimen

3.2 载荷谱

载荷谱分为2类：谱1为起落架基准谱，代表了在基准使用状态下受载情况。谱2～谱4为3个起落架单机载荷谱，载荷谱均为飞续飞形式，每个载荷谱均代表500次飞行起落。

为了表明DTW方法可以区分载荷谱的相似程度，对基准载荷谱进行小载删除，见图6。删除每次起落中峰值小于40%最大载荷，谷值大于0的载荷循环，得到谱1-1，删除循环占总循环数70%。采用当量损伤方法分别计算谱1与谱1-1的当量损伤，得到谱1-1与谱1的损伤比值为0.954，表明删除的载荷循环对损伤基本没有影响。观察图6，可见删除小载之后载荷谱形式发生了较大变化。对各个载荷谱进行雨流计数，将取出的载荷循环绘制成载荷-超越数曲线，见图7。图7中横轴为各载荷谱峰值应力与基准谱最大应力的比值，纵轴为各级载荷超越数与基准谱循环数的比值。

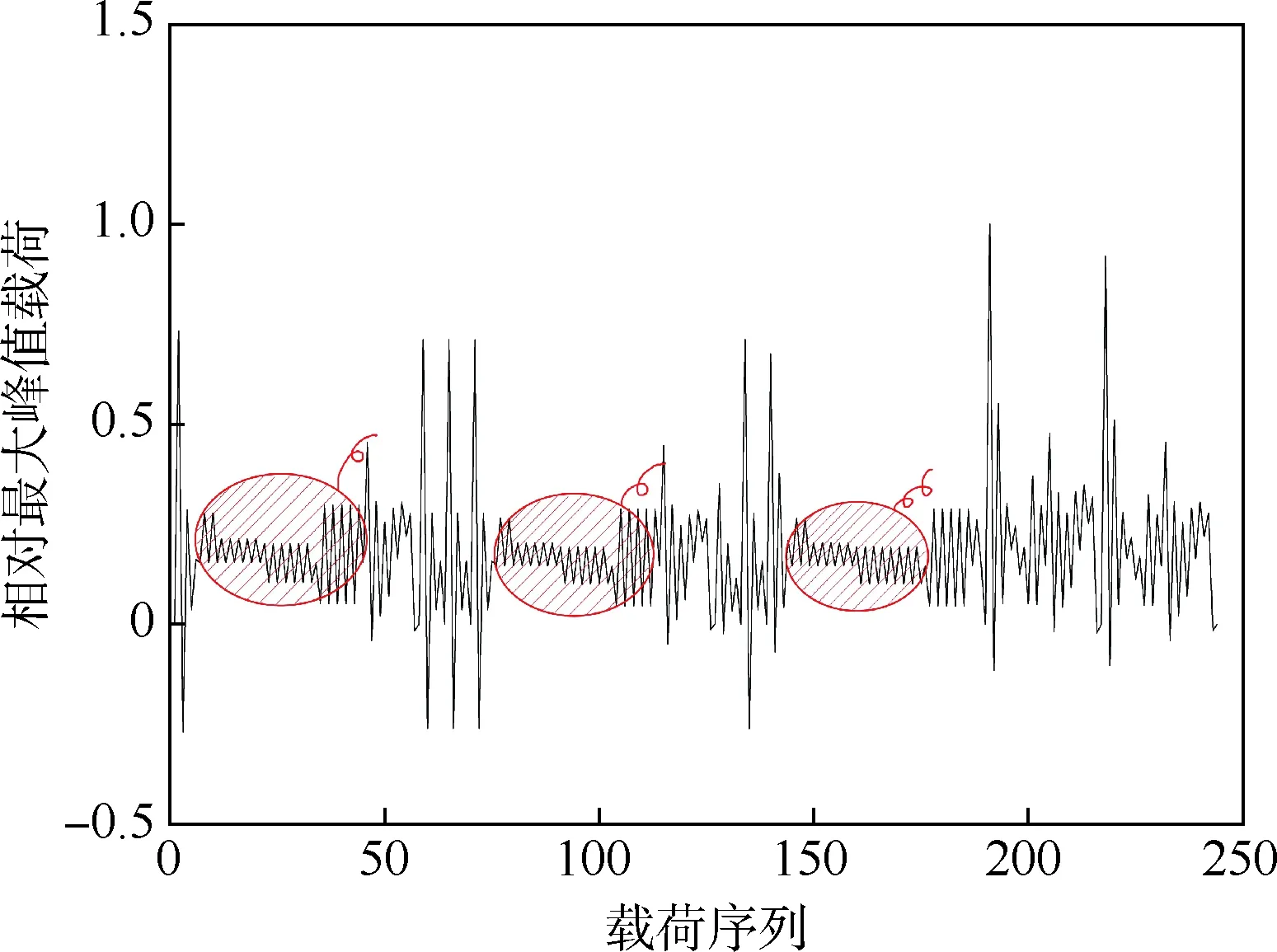
图6 谱1部分载荷序列Fig.6 Fractional load sequence of Spectrum 1

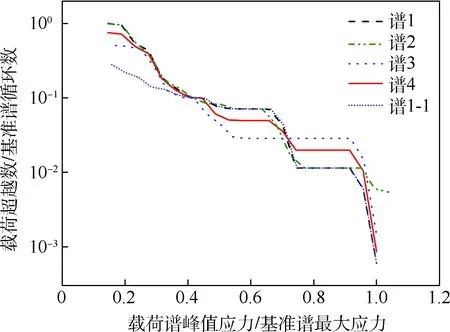
图7 起落架载荷谱相对峰值-相对超越数曲线Fig.7 Relative peak-relative excess curves of landing gear load spectrum

3.3 实验结果

疲劳实验在MTS880-500 kN电液伺服疲劳实验机上进行。试件直接夹持在实验机夹头上，在室温大气环境下沿轴向加载，加载波形为正弦波，实验频率为5 Hz，加载至破坏。图8显示了基准谱加载情况下的断口图片，观察断口发现，在圆弧过渡区域萌生表面多源裂纹，选取最先萌生的为主裂纹。使用光学显微镜对试件断口进行判读，可以得到裂纹扩展的(L，N)数据，其中L为裂纹前缘距试件表面距离，N为飞行起落数，图9列出了得到的谱1下的(L，N)数据。在纵轴为对数坐标下，L-N曲线大致呈直线，符合相对小裂纹扩展规律。对(L，N)数据采用三点拉格朗日插值方法确定沿孔径方向指定裂纹长度对应的裂纹萌生寿命。取裂纹长度为0.8 mm对应的疲劳寿命为裂纹萌生寿命。假定裂纹萌生寿命服从对数正态分布[19]，对数正态分布的均值与方差计算方法如下:

(14)

式中：Ni为疲劳裂纹萌生寿命；h为有效试件数量；N50为中值寿命；s为中值寿命标准差。对各个载荷谱采用当量损伤方法进行寿命预测，以基准谱谱1的寿命为基准计算其他载荷谱下的疲劳寿命，结果见表1。图8为典型断口图片，图9中01～05为谱1下进行疲劳实验的5件试件。

图8 谱1下典型试件断口Fig.8 Typical fracture surface of specimen under Spectrum 1

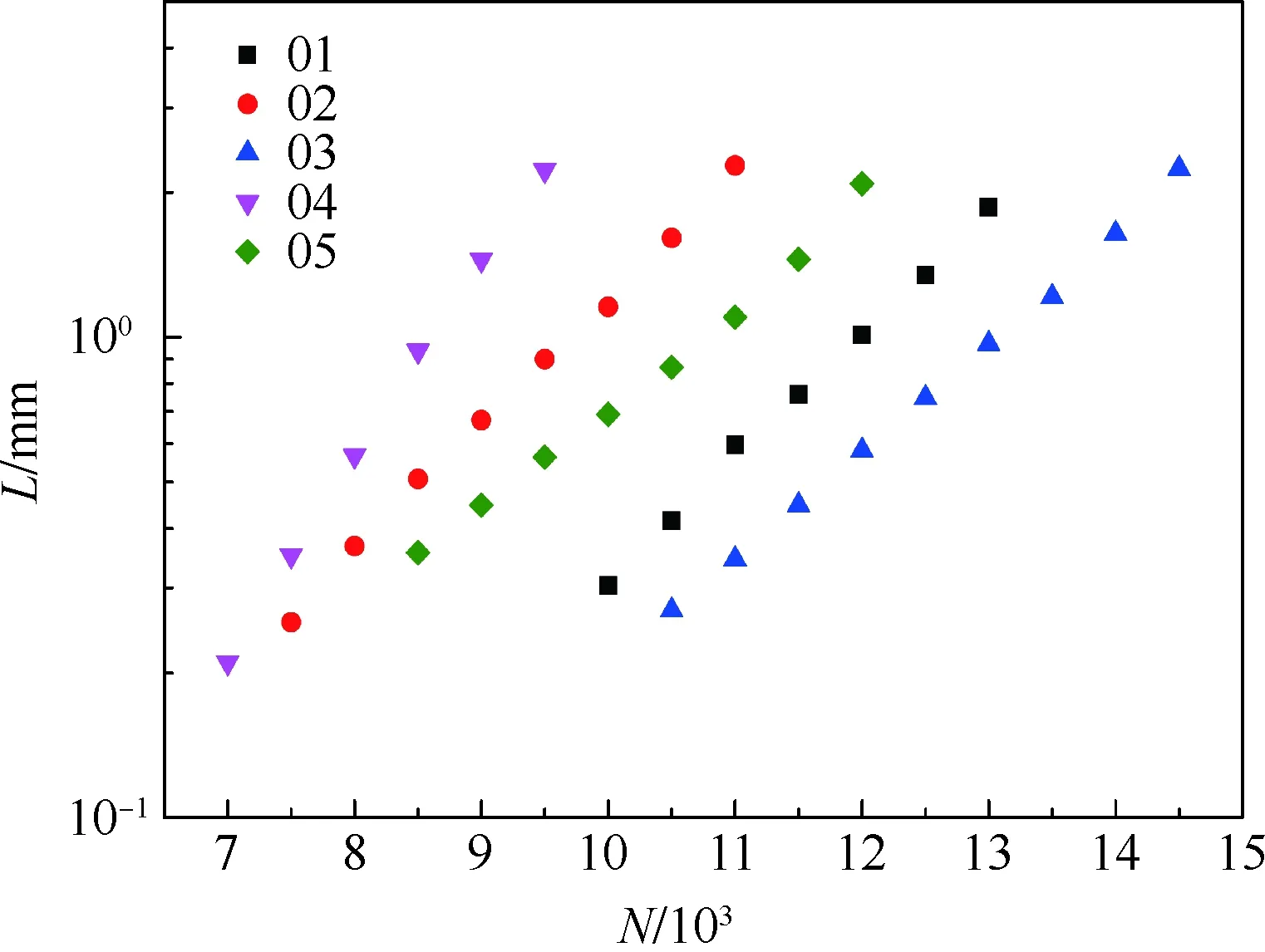
图9 谱1下主裂纹扩展(L,N)数据Fig.9 Lead crack growth (L,N) data corresponding to Spectrum 1

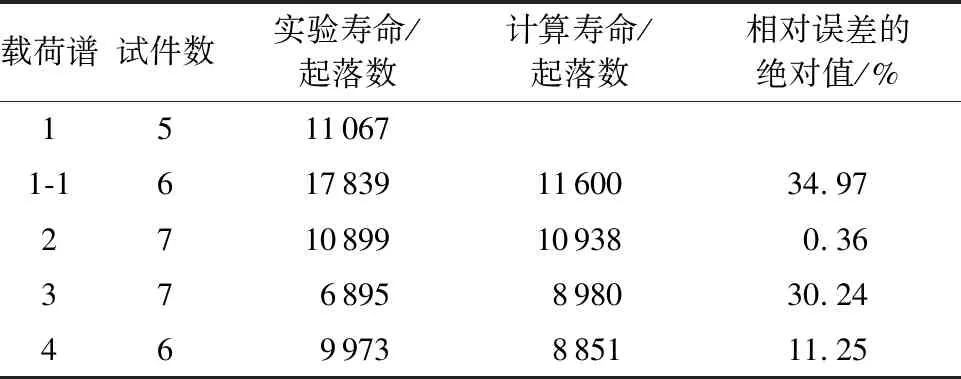
载荷谱试件数实验寿命/起落数计算寿命/起落数相对误差的绝对值/%15110671-16178391160034.972710899109380.36376895898030.24469973885111.25

3.4 损伤计算精度与载荷谱相似度的关系

采用2.3节DTW方法计算3.2节中4个载荷谱与基准谱的DTW距离。结合2.3节中损伤计算误差结果，结果见表2与图10，图中横轴为各个单机谱与基准谱的DTW距离，纵轴为损伤计算的相对误差的绝对值E，相对误差的绝对值与DTW距离呈正相关。

表2 单机谱与基准谱之间的DTW距离Table 2 DTW distance between individual spectrum and reference spectrum

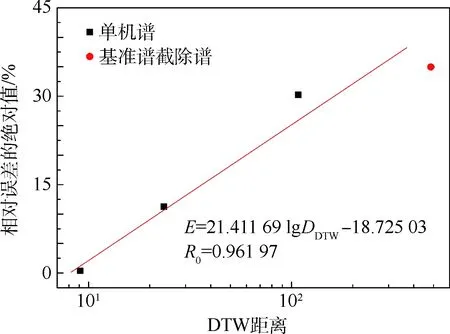
图10 DTW距离与损伤计算误差的关系Fig.10 Relationship between DTW distance and damage calculation error

3.5 结果分析

1) 谱1与谱1-1的寿命存在明显区别，采用当量损伤方法，计算得到谱1-1的寿命为11 600次起落，与谱1的11 067次起落差别可以忽略不计，这是由于谱1-1通过截除谱1中的小载荷循环得到，采用疲劳分析方法，小载荷循环造成的损伤可以忽略不计。然而在起落架载荷谱中这些低载荷与高载荷共同作用，对结构寿命产生复杂的影响，删去这些小载荷循环后，载荷谱的构成形式与交互作用均发生改变。实验结果显示谱1-1的寿命与谱1相比增加了61%，寿命计算误差达到了34.97%。由于谱1-1为谱1截除小载荷后的结果，载荷谱形状存在很大差别，可以通过DTW距离反映。谱1-1与谱1的DTW距离为421.5，而其余3个单机谱最大的DTW距离为134.9，差异明显。

2) 上述4个起落架谱寿命计算误差随DTW距离增加而增大，在对数坐标下与相对误差与DTW距离近似呈线性关系，对4个单机载荷谱计算结果进行回归分析，拟合得到到回归直线为E=21.411 69 lgDDTW-18.725 03，回归系数R0为0.961 97。若以计算误差为20%作为误差极限，通过上式计算的DTW临界值为64.36。4个载荷谱中谱3与谱1-1的DTW距离超过此临界值，需要单独处理。实验结果表明这两个谱的计算误差均超过了30%。

4 讨论

将DTW方法分析结果与SSF方法对比。采用式(9)计算3.2节的5个载荷谱的SSF,其中采用当量损伤方法进行等损伤折算。

(15)

式中:Dmax,cycle为谱中最大循环的当量损伤值。通过SSF的定义易知，当SSF=0,载荷谱为等幅谱，当SFF越大，载荷谱中小载荷数量越多。得到5个载荷谱的SSF结果，见表3。

表3 不同载荷谱SSF结果Table 3 SSF results of different load spectra

表3中结果显示，谱1与谱2、谱3、谱4的SSF相差不大，由于4个谱均采用相同的载荷谱编制技术得到，其高载荷、低载荷的比例具有一致性，然而谱3的损伤计算误差为30.23%，无法直接通过SSF加以判别，进而无法确定单机谱SSF值与基准谱的近似程度是否与损伤计算误差相关。而谱1与谱1-1的SSF值分别为1.195和0.672，差异明显，表明SSF方法可以区分基准谱谱1与删除小载后的谱1-1。这主要是因为SSF仅能区分载荷谱中载荷循环大小和数量，不能区分载荷的顺序。而采用DTW方法综合考虑载荷序列的相似程度，可以得到单机谱的DTW距离与计算误差绝对值呈正相关。

本文方法仅针对起落架载荷谱这类特殊的载荷谱，其构成单一，本身就具有一定的相似性。对于其他形式载荷谱适用性仍需要检验。