钻井船型线优化及月池附加阻力研究*

张 琪 陈 鸽 张利军 曹 凯 段 菲

(中远海运重工有限公司技术研发中心 大连 116600)

0 引 言

钻井船作为目前海洋油气开采工艺过程中最为重要的装备之一，移动方式主要有自航和拖航两种.具有自航能力的钻井船，由于移动灵活，能够满足频繁的调遣需求.设计钻井船的航速指标通常在10 kn以上，因此在满足钻井船各项布置需求的前提下，通过型线优化使其具备优良的快速性是十分重要的.此外，钻井船出于作业需要，通常在靠近船舯位置存在一个垂向贯通式开口，这个开口结构即为月池.由于月池的存在使得钻井船在航行过程中阻力增加，低航速时附加阻力可占全船阻力的10%～15%，高速时甚至可达100%[1]，因此，月池对钻井船阻力性能的影响是研究钻井船快速性重点要考虑的因素.

近些年随着数值模拟技术的飞速发展，针对三大主力船型首部型线优化做了大量的研究.熊小青等[2]结合人工设计经验，借助CFD技术对两型尺度参数相近的灵便型油船完成了兼顾多个吃水的首部型线优化；张文山等[3]基于球首参数化表达和NURBS理论，对母型球首构型进行参数优化构建，并利用CFD软件进行仿真计算，与母型构型进行阻力和波形对比完成了球艏的优化；邓贤辉等[4]基于iSIGHT 优化设计平台，将遗传算法与二次序列规划法相结合的组合优化方法应用于某双艉集装箱船的阻力优化，所提出的方法具有较强的工程适用性.而针对钻井船型线的设计优化并不多见，常见的钻井船快速性研究主要集中在对月池的分析上，Erik等[5]基于OpenFOAM对二维月池内部的流动特性进行了计算分析，在此基础上拓展到了三维月池的阻力预报研究；Riaan等[6]通过系列模型试验对月池内的流体振荡进行了分析，并构建了基于月池内“活塞”振荡预报月池增阻的理论方法，验证的结果表明预报结果与试验结果吻合良好；黄祥宏等[7]通过观察试验现象并结合数值模拟的后处理软件对月池内的流体运动形式及月池内流体对月池壁的作用进行了分析，对月池导致阻力增加的原因给出了合理解释.

文中应用CFD方法对某钻井船进行了型线优化，并对月池产生的附加阻力及该附加阻力与主船体型线的关联度进行了分析，为计及月池附加阻力的钻井船型线优化设计提供参考和借鉴.

1 研究对象及数值计算方法

1.1 研究对象

以某钻井船作为研究对象，其主要参数信息见表1.

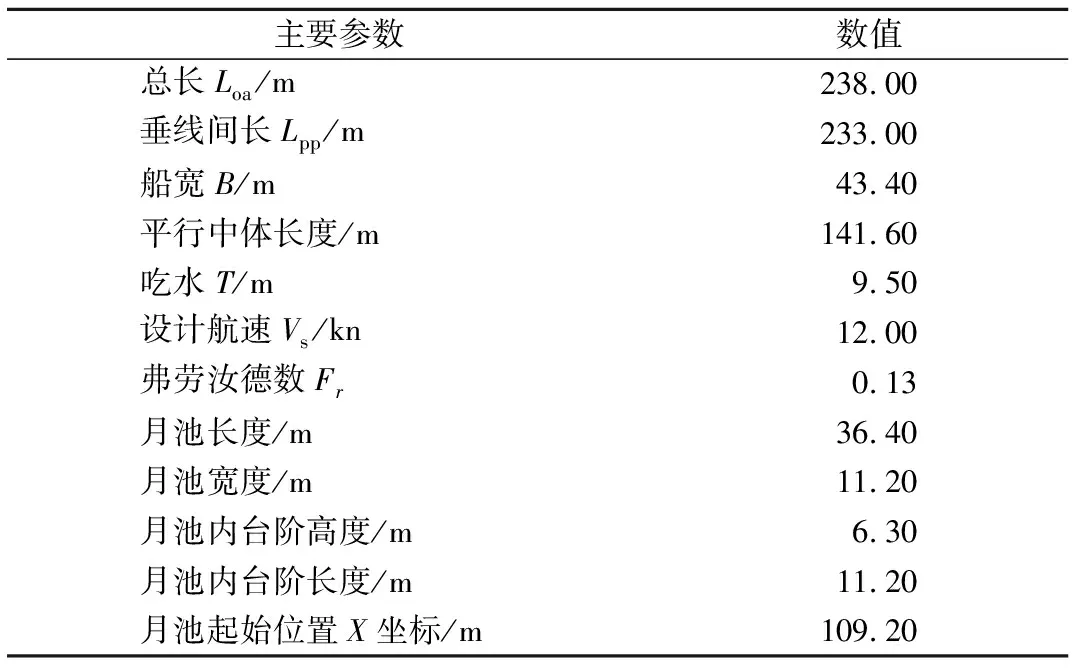
表1 钻井船主要参数信息

首先利用CAESES软件，对钻井船进行了全参数化建模，为型线优化提供可以基于参数调整实现型线变化的几何模型，建好的参数化模型见图1.

图1 钻井船母船型几何模型(方案A0)

1.2 数值计算方法

数值计算统一采用RANS模型框架下的SSTk-ω模型，SSTk-ω湍流模型是融合了k-ω湍流模型与k-ε湍流模型两种湍流模型的理论构建的，并且考虑了湍流剪切力的输运效应，可以精准地计算出逆向压力梯度引起的流动分离位置和作用区域.SSTk-ω模型中k和ω的输运方程[8]分别为

Pk-β*ρkω

(1)

(2)

式中：xi，xj为空间分量；Pk为湍流动能生成项；为湍动黏性系数；Uj为坐标轴xj方向上的平均速度分量；S为平均应变率张量；F1为混合函数；k，α，β，σω，σω2为湍流模型常数.

自由液面的变化采用VOF法来捕捉，假设计算区域是V，将其分成两个区域，流体A所在的区域记为V1，而流体B所在的区域记为V2.定义这样一个函数(表征流体质点所在的区域)：

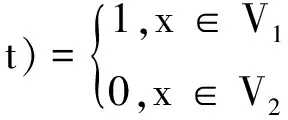
(3)

对于由两种不相容的流体组成的流场，α(x,t)满足：

▽α=0

(4)

式中：U为流体的速度场.

在每个网格Iij上定义Cij，Cij为α(x,t)在网格上的积分：

(5)

该函数称之为VOF函数，若数值在0～1，那么该网格为自由液面处的网格，一系列这样的网格单元组成了自由液面.

2 型线优化

2.1 船首优化

为简化钻井船型线优化的计算量，假定月池产生的附加阻力是固定的，在仅考虑月池闭合的状态下，对钻井船的主船体型线进行了优化.基于兴波阻力的计算优化了船首的型线，在完成首部型线的基础上通过经验对船尾型线进行了优化.

基于钻井船的全参数化模型，通过CAESES软件与SHIPFLOW软件构建型线优化平台对首部做基于势流计算的阻力优化，采用遗传算法(NSGA-Ⅱ)对最优设计方案进行了100次型线方案搜索，通过对船首的水线形状、入水角以及首部的丰满度的控制参数进行优化，最终确定了首部型线最佳的设计方案A1.然后通过CFD方法对模型尺度的型线的总阻力进行了预报，几何模型的缩尺比为36，计算结果见表2.设计方案A1较初始方案A0的总阻力降低了1.12%，其中优化后的摩擦阻力增加了0.24%，变化幅度不大，而压阻力降低了3.92%，使得总阻力随之下降.船首优化前后的横剖线对比见图2，其中实线代表型线A0，虚线代表型线A1.

表2 船首优化前后的阻力值

图2 船首优化前后的横剖线对比

图3为优化前后的自由表面兴波对比图，由图3可知，优化后的型线方案A1较方案A0船身附近的横波有所减弱，但并不明显，而图4中给出的船首底部压力分布差别较大，方案A0船底的低压力等值线更为集中，而经过优化后的A1方案低压区明显得到改善.

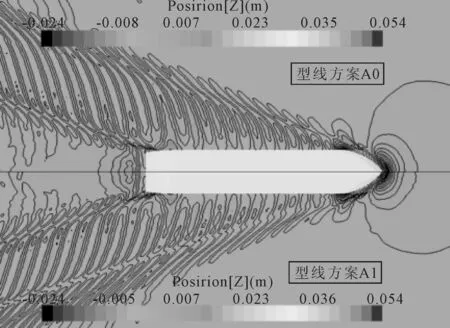
图3 优化前后的自由表面兴波对比

图4 优化前后的首部压力分布对比

2.2 船尾优化

以型线方案A1为基础，对尾部模型进行了修改，方案A1考虑到船尾末端需要安装两个全回转推进器，将船尾末端设计为水平形式.优化过程中将船尾修改为缓慢斜升，安装推进器的位置布置两处水平基座，得到型线方案A2，船尾修改前后的几何模型对比见图5.优化后的船模(缩尺比λ=36)静水阻力计算结果见表3，与之前的设计方案相比，方案A2较方案A1的阻力降低9.64%，较A0阻力降低了10.65%.

图5 船尾修改前后的几何模型对比

型线方案总阻力/N摩擦阻力/N压阻力/N优化效果/%A222.3216.805.529.64

由表3可见，尾部经过优化，总阻力得到非常明显的改善，其中摩擦阻力几乎没变，主要是压阻力大幅降低了.方案A2尾部的主要改动在于尾部由水平改为缓慢斜升，尾封板最底端向上抬升，使得船尾的压力分布更加均匀，见图6，同时尾部的流体运动更加顺畅，减少了能量的损失.此外，方案A2尾部添加的两处水平基座对流动必然存在局部的扰动作用，导致一定的阻力增加，但相比于优化后整个尾部的阻力收益，影响不大.

图6 优化前后船尾压力分布对比

3 月池附加阻力研究

3.1 独立月池受力计算

目标钻井船选定的月池方案为阶梯型，月池长度为36.4 m、宽度为11.2 m，月池内部在靠近船首方向设置一个长度为11.2 m，高度为6.3 m的台阶.对月池进行CFD计算的模型仍然采用模型尺度，缩尺比(λ=36)与主船体模型保持一致.为保证月池的来流和去流方向不受钻井船首、尾部型线影响，只保留船体的平行中体型线，并一直延伸至计算域的入口和出口.其中，月池到入口的距离取3倍的月池长度，月池到出口的距离取8倍的月池长度，月池的几何模型及计算域大小见图7.

图7 月池的几何模型及计算域

湍流模型选取SSTk-ω.由于月池内部的流动较为复杂，为了更好的捕捉月池内部的流动现象以及受力，需要对计算域中月池内部的网格进行重点加密.为说明月池内的网格尺寸选取的合理性，通过改变月池内部的网格尺寸进行了月池受力计算的网格无关性验证.对应实尺度下的月池吃水为9.5 m，航速为12 kn，结果见表4.

表4 网格无关性计算结果

由表4可知，当网格数目达到174万后，网格再次增加对计算结果的影响已经很小，仅为1.88%.由此可以看出2号网格方案用于计算月池受力是合理的，后续与月池相关的计算均参照2号网格方案进行网格划分.

3.2 月池附加阻力计算

为研究月池产生的附加阻力,需比较船舶在静水中航行时月池开启及关闭状态下的阻力变化，其中月池关闭状态的阻力已在型线优化阶段完成，通过CFD软件计算月池开启状态下的阻力在方法上与月池关闭状态下类似.只是在监测受力时，除了监测模型受到的总阻力、摩擦阻力、压阻力三种阻力之外，为了很好的研究月池产生的阻力情况，人为的将主船体和月池分割成两个部分，并监测这两部分各自的受力情况.监测到的型线A0和A2在月池开启状态下受力曲线与独立月池的受力曲线比较见图8.

图8 月池受到的阻力曲线

目前共计算了钻井船月池关闭、独立月池以及月池开启三种状态下的阻力，计算过程中监测的水气分界面示意图见图9.为了方便比较，将三种情况下计算得到的阻力进行汇总得到表5.

图9 不同计算对象的水气分界面示意图

表5 月池及主船体阻力计算结果 N

由表5可知，在钻井船月池开启状态下，型线方案A0及A2的静水阻力均有所增加，阻力值较月池关闭状态分别增加了3.80 N(15.2%)和3.72 N(16.7%).此外，两种型线方案中月池附加阻力均较月池开启状态下的月池受到的阻力小，分析原因主要是月池开启后，船底的湿表面积减少了，且月池内部侧壁受到的摩擦阻力很小，可以忽略不计，因此，月池开启后产生总的摩擦阻力降低了.观察主船体受力也可以发现，月池开启状态下的主船体受力明显较月池关闭状态的主船体受力小.为比较月池受到阻力与型线变化间的关系，定义月池所受阻力随型线变化的关联度为σ，通过表征不同型线方案中月池的受力与独立月池之间的变化量，来衡量不同型线方案对月池受力的影响，为

(5)

式中：Ri为型线i在月池开启时受到的阻力；Rmp为独立月池受到的阻力.

由式(5)可知，型线方案A0的月池受力关联度σA0=1.88%，型线方案A2的月池受力关联度σA2=6.57%.由计算结果可知，从型线方案A0到A2的月池受力较独立月池受力发生了变化，但变化幅度不大.比较表5中型线优化前后的月池附加阻力，优化后的型线方案A2月池附加阻力较优化前仅相差2.11%(而且月池产生的附加阻力相较于钻井船航行时的总阻力占比不到17%).此外，通过比较优化后总阻力减少量可以看出月池开启对型线优化前后的总阻力收益变化的影响是有限的.综合上述分析可知，本次在月池关闭条件下优化得到的钻井船型线方案，在月池开启状态下同样能够获得近似的阻力收益.

4 结 论

1) 钻井船的首、尾部型线经过优化，总阻力得到了大幅改善，其中通过船尾优化获得的总阻力降低更显著，由此可见，对于钻井船这种低速船舶，尾部的优化在型线设计过程中十分重要，优化得当可获得十分可观的阻力收益.

2) 钻井船月池产生的附加阻力较月池关闭状态下的总阻力增加16%左右，由于月池附加阻力随着吃水、航速，以及不同月池形状的变化均有不同程度的变化，因此，在评估钻井船的快速性能时需要对月池附加阻力重点关注.

3) 实际工程应用过程中，建议在型线优化开始之前，首先通过比较月池受到阻力与主船体型线之间的关联度来确定主船体对月池受力变化的影响程度.当关联度较低时，在优化过程中可按照月池关闭状态进行型线优化，有利于在设计方案筛选阶段大幅缩减计算量；反之，当关联度较高时，型线优化的过程则需要考虑首、尾部型线变化对月池附加阻力的影响.此外，对于月池与主船体之间相互影响的关联度大小与船体的长宽比、平行中体长度、月池布置的位置、航速等因素之间存在的联系还有待做进一步研究.