环R+uR+vR+uvR上的斜常循环码
2019-04-28宋贤梅
刘 玮,宋贤梅
(安徽师范大学数学与统计学院,安徽芜湖241003)
众所周知,循环码是编码中的一种重要码,它能够高效快速完成译码过程,从而在实践中得到广泛的运用。1994年,Hammons等证明了某些二元非线性码可以看作是Z4上的循环码Gray像[1]。自此之后,有限链环及一些特殊的有限链环上的循环码及其相关的研究受到越来越多的关注。万哲先等系统介绍了Galois环上的循环码[2];Wolfman等研究了Z4上的负循环码与循环码[3];Dinh研究了Galois环上长为偶数的负循环码[4];钱建发研究F2+uF2上(1+u)-常循环码和循环码[5];朱士信等研究了Fp+uFp上的常循环码和Gray像[6];Boucher等首次提出了Fp上的斜循环码概念[7],并说明斜循环码的汉明距离大于已知最好的线性码,其后又研究了Galois环上的斜常循环码[8];Jitman等研究了有限链环上的斜常循环码及对偶码[9];宋贤梅等研究了非有限链Fq+vFq+v2Fq上的斜常循环码及对偶码的相关性质[10]。随着环的不断推陈出新,环之间存在着一定的局限性和关联性,从最开始普通的循环码逐步研究到更深层次的斜循环码,到目前的斜常循环码并取得丰富的结论。因不同环上的斜常循环码具有相似的结论,所以本文构造全新的环来研究上述文献中的结论和性质。针对环ℜ=R+uR+vR+uvR(u2=-u,v2=-v,uv=vu)上的斜常循环码及对偶码性质,得到线性码C是斜常循环码的充要条件,并讨论斜常循环码C的生成多项式与对偶码C⊥的生成多项式。
1 预备知识
记环ℜ=R+uR+vR+uvR,其中u,v满足u2=-u,v2=-v,uv=vu,R为有限链环。 r表示有限链环R的极大理想且rl=0,l为其幂零指数,则R r是域,记为K。记 ||K =q,则 ||R =ql。令e1=1+u+v+uv,e2=uv,e3=-u-uv,e4=-v-uv,令ei=∈ R,i=1,2,3,4,且当i≠ j,eiej=0,e1+e2+e3+e4=1,因此有直和分解
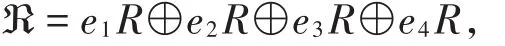
且ℜ中元素r可唯一表示为
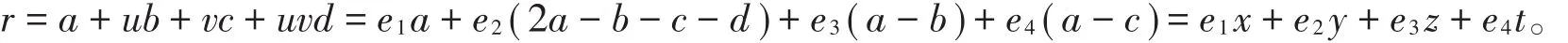
易知1+2u是环ℜ的一个单位,且满足(1+2u)e1=e1,(1+2u)e2,(1+2u)e3=-e3,(1+2u)=e4,ℜn={(a0,a1,…,an-1)|ai∈ℜ,i=0,1,…,n-1 }是一个交换环。若C是ℜn的非空子集合,则称C是ℜ上长为n的码。若C是ℜn的R-子模,称C是R上长为n的线性码。
设X=(x1,x2,…,xn),Y=(y1,y2,…,yn)∈ℜn,定义X,Y的欧几里得内积为
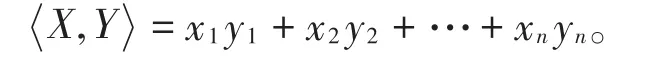
设C是长为n的码,C⊥={ }x∈ℜn|x,c=0,∀c∈C 称为C的欧几里得对偶码。
设θ是有限链环R的一个自同构,定义ℜ上的自同构θˉ满足:

ℜ到R4的Gray映射ϕ定义为对任意r=a+ub+vc+duv∈ℜ有
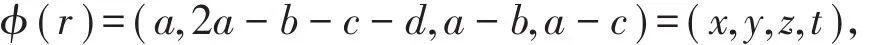
扩展到ℜn上,则对任意r=a+ub+vc+duv∈ℜ,其中ci=e1xi+e2yi+e3zi+e4ti(i=0,1,2,…,n-1)有
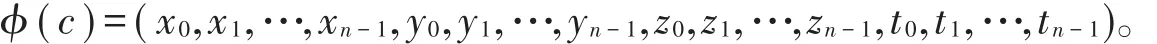
设C是ℜ长为n的线性码,对c∈C,c的Gray重量为WG(c)=WH(x,y,z,t),易知ϕ是ℜn到ℜ4n的双射且是一个保距映射。
下面给出码的直和与卡氏积定义,设B1、B2、B3、B4是ℜ上长为n的线性码,
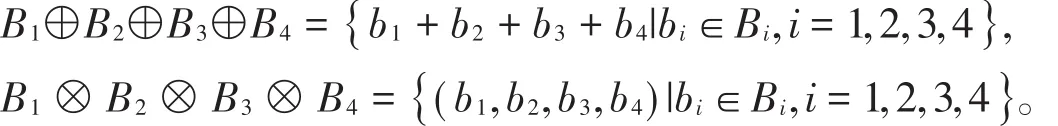
假设C为环ℜ上长为n的线性码,定义集合:

易知:
(1)Ci(i=1,2,3,4)是R上长为n的线性码;
(2)线性码C可以唯一表示为e1x⊕e2y⊕e3z⊕e4t;
(3)C= |C1|⋅| C2|⋅|C3|⋅|C4|。
通过线性码C的直和分解可以得到C的对偶码C⊥及ϕ(C⊥)与ϕ(C)⊥的相关性质,从而得到如下命题。
命题1设C=e1C1⊕e2C2⊕e3C3⊕e4C4是ℜ上长为n的线性码,则下面结论成立:
(1)C⊥=e1C1⊥⊕e2⊕e3⊕e4,
(2)ϕ(C)=C1⊗C2⊗C3⊗C4且 | ϕ(C)|= |C1|⋅| C2|⋅|C3|⋅| C4|,
(3)ϕ(C⊥)=C1⊥⊗ C2⊥⊗ C3⊥⊗ C4⊥。
证明(1)定义集合={x∈ Rn|∃y,z,t∈ Rn,e1x+e2y+e3z+e4t∈ C⊥},同理定义,易知 C⊥=e1⊕e2⊕e3⊕e4。下面仅需证明=(i=1,2,3,4),不妨证=,对任意x ∈,有e1x+e2y+e3z+e4t=c′∈ C⊥,因此对任意x′∈ C1,有e1x′+e2y′+e3z′+e4t′=c∈ C且< c,c′>=e1xx′=0,从而xx′=0,则⊆。另一方面,若x∈,则c′=e1x′+e2y′+e3z′+e4t′∈ C⊥,有< e1x,c′>=e1xx′=0,于是x∈ ℓ⊥1,故=。同理可证=,=,=,所以 C⊥=e1+e2+e3+e4。
(2)由线性码C的直和表示及ϕ的定义,易知ϕ(C)⊆C1⊗C2⊗C3⊗C4。对任意c=(x,y,z,t)∈C1⊗C2⊗C3⊗C4,令 r=e1x+e2y+e3z+e4t,则 r∈C 且 ϕ(r)=c=(x,y,z,t),故C1⊗C2⊗C3⊗C4⊆ϕ(C)。因此ϕ(C)=C1⊗C2⊗C3⊗C4,注意到ϕ是双射,所以
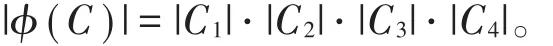
(3)由(1)(2)以及ϕ的定义易知ϕ(C⊥)⊆ϕ(C)⊥且注意到ϕ是双射,于是
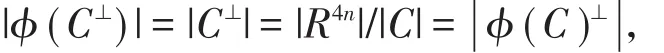
所以ϕ (C⊥)= ϕ (C)⊥,类似(1)的证明有ϕ (C)⊥=⊗⊗⊗。
2 环ℜ上的斜常循环码
定义1设是ℜ上的自同构,λ是ℜ的单位,ρθˉ,λ是ℜn的自同态,若对任意c=(c0,c1,…,cn-1)∈ C有ρθˉ,λ(r0,r1,…,rn-1)=(ˉ(λ)ˉ(rn-1),ˉ(r0),…,ˉ(rn-2))∈ C,则称码C是斜常循环码或- λ-常循环码。 特别地,当λ=1时,称C为斜循环码;当λ=-1时,称C为斜负循环码。
引理1设n为正整数是ℜ的一个自同构,xn-(1+2u)∈ℜ[x;,则下列说法等价:
(1)〈xn-(1+2u)〉是ℜ [x;的双边理想;
(3)xn-(1+2u)是ℜ [x;的中心。
证明(3)⇒(1)显然。
(1)⇒(2)对任意的 ax∈ℜ,由条件(1)知 ax(xn-(1+2u))=(xn-(1+2u))ax,即 a(1)xn+1-1+2u)x=(a)xn+1-(1+2u)ax,比较系数得(a)=a,即|<> ||n且(1+2u)=1+2u。
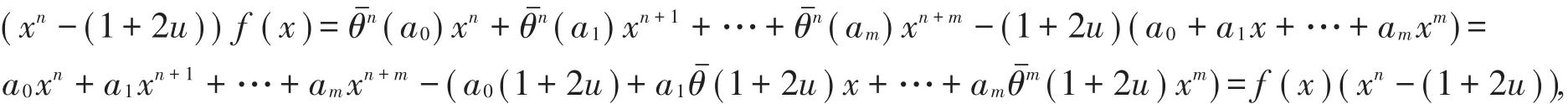
所以xn-(1+2u)是ℜ [x;的中心。
注下面讨论的内容,均是在〈xn-(1+2u)〉是双边理想的前提下,因此需要条件θˉ的阶整除n,θ(1+2u)=1+2u。
定理1设C=e1C1⊕e2C2⊕e3C3⊕e4C4是ℜ上长为n的线性码,则C是θˉ-(1+2u)-常循环码当且仅当C1、C4是ℜ上长为n的斜循环码,C2、C3是ℜ上长为n的斜负循环码。
证明设r=(r0,r1,…,rn-1)∈C,其中ri={e1ai+e2bi+e3di+e4di∣ai,bi,ci,di∈R(i=0,1,2,…,n-1)},令a=(a0,a1,…,an-1),b=(b0,b1,…,bn-1),c=(c0,c2,…,cn-1),d=(d0,d1,…,dn-1),可知
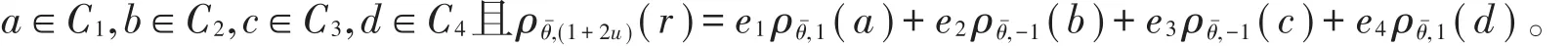
因此 ρθˉ,(1+2u)(r)∈ C 的充分必要条件是 ρθˉ,1(a)∈ C1,ρθˉ,-1(b)∈ C2,ρθˉ,-1(c)∈ C3,ρθˉ,1(d)∈C4,即 C 是 ℜ 上长为n的斜常循环码的充分必要条件是C1、C4是ℜ上长为n的斜循环码,C2、C3是ℜ上长为n的斜负循环码。
命题2设C=e1C1⊕e2C2⊕e3C3⊕e4C4是ℜ上长为n的(1+2u)-线性码,gi(x)是Ci的生成多项式,且i=1,4时,gi(x)右整除xn-1;当i=2,3时,gi(x)右整除xn+1,则存在唯一的g(x)=e1g1(x)+e2g2(x)+e3g3(x)+e4g4(x)∈ ℜ [x;,使得C=< g(x)>,g(x)右整除xn-(1+2u)且|C|=
证明令g(x ) =e1g1( x ) +e2g2( x ) +e3g3( x ) +e4g4( x ),下证C=<g(x)>。 一方面,易知C⊆〈e1g1(x),e2g2(x),e3g3(x),e4g4(x)〉,而eigi( x ) =eig( x )(i =1,2,3,4),可得C⊆〈g(x)〉。另一方面注意到g(x)∈C,故C=〈g(x)〉。
现证g(x)右整除xn-(1+2u)。由条件可得存在fi(x)∈ ℜ[x;(i=1,2,3,4),使得
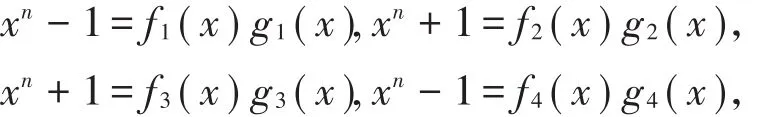
由于(1+2u)e1=e1,(1+2u)e2=-e2,(1+2u)e3=-e3,(1+2u)e4=e4,于是

故g(x)是xn-(1+2u)的右因子。
最后,由于|C|=|C1|⋅|C2|⋅|C3|⋅|C4|,gi(x)是Ci的生成多项式,因此
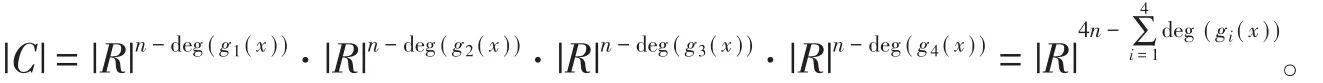
3 斜常循环码的对偶码
下面讨论环ℜ上长为n的斜常循环码的对偶码与其之间的联系,并给出斜常循环码的生成多项式。
定理2设θˉ的阶是2且n为偶数,C是ℜ上长为n的线性码,则C是θˉ-(1+2u)-常循环码当且仅当C⊥是θˉ-(1+2u)-1-常循环码。
证明假设C是θˉ-(1+2u)-常循环码,对任意u=(u0,u1,…,un-1)∈C有如下等式成立因此对任意v∈C⊥有0=〈(u),v〉,


从而
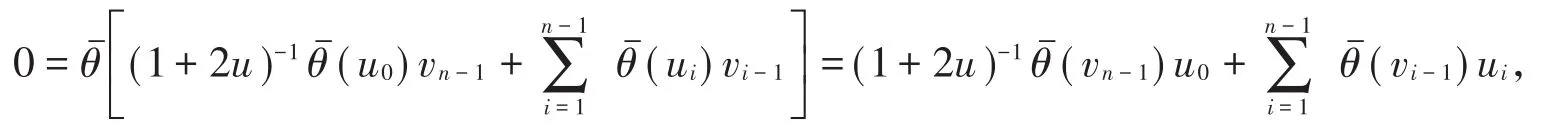
即〈(1+2u)-1θˉ(vn-1),θˉ(v0),…,θˉ(vn-2),(u0,u1,…,un-1)〉 =0,所以(1+2u)-1θˉ(vn-1),θˉ(v0),…,θˉ(vn-2))∈ C⊥,即 C⊥为θˉ-(1+2u)-1-常循环码。
反之设C⊥为 θˉ-(1+2u)-1-常循环码,利用前面类似的结论及(1+2u)-2=1 易知 C=(C⊥)⊥是θˉ-(1+2u)-常循环码。
引理2设a(x)=a0+a1x+a2x2+ …+an-1xn-1,b(x)=b0+b1x+ …+bn-1xn-1∈ℜ[x;θˉ],则下面三条性质等价:
(1)当i∈{0,1,2,…,n-1}时,a(x)的系数向量与xi(xn-1φ(b(x)))的系数向量欧几里得正交。
(2)(a1,a2,…,an-1)与(bn-1,θˉ(bn-2),…,θˉn-1(b0))以及它的θˉ-(1+2u)-常循环移位正交。
(3) 在ℜ [x;θˉ]/(xn-(1+2u))中,a(x)b(x)=0。
定理3设|<θˉ>|=2,且n为偶数,C是ℜ上长为n的θˉ-(1+2u)-常循环码,g(x)是其首一的生成
(1)斜多项式xdeg(h(x))φ(h(x))是xn-(1+2u)的右因子。
(2)C⊥是由xdeg(h(x))φ (h(x))生成的θˉ-(1+2u)-1-常循环码。
证明(1)由条件有|< θˉ> |∣n,且θˉ(-(1+2u))=-(1+2u),于是
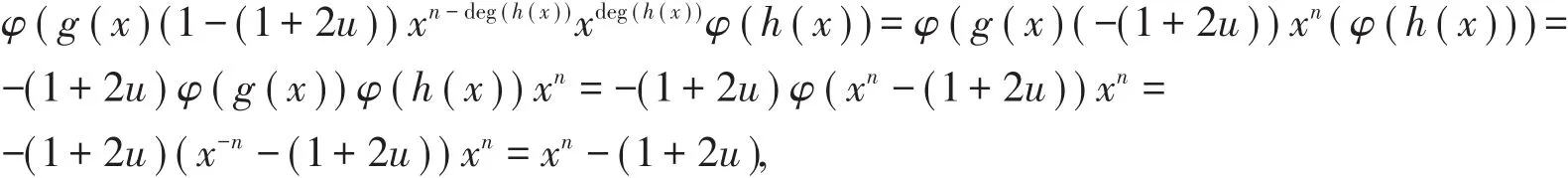
从而xdeg(h(x))φ (h(x))是xn-(1+2u)的右因子。
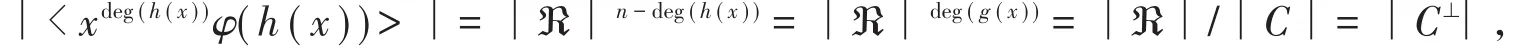
所以< xdeg(h(x))φ(h(x))〉=C⊥。
