行为负相协随机变量阵列加权和的矩完全收敛性
2019-04-28郭明乐刘锦然
郭明乐,刘锦然
(安徽师范大学数学计算机科学学院,安徽芜湖241003)
Hsu和Robbins及Cai研究NA(Negatively Associated)随机变量加权和的完全收敛并得到了如下结论[1-2]后,人们对完全收敛性的关注越来越多。
定理1 设{X,Xn,n≥1}是同分布的NA随机变量序列,{αni,1≤i≤n,n≥1}是实数阵列,对某个0<α≤2满足

设bn=n1α(log n)1γ,这里γ > 0,当1< α ≤ 2时,EX=0。若对某h > 0,有Eexp(h|X|γ)< ∞,则任意ε> 0,有

Sung[3]弱化一些矩的条件,从而改进了定理1,得到如下定理。
定理2设{X,Xn,n≥1}是同分布的NA随机变量序列,{αnιi,1≤i≤n,n≥1}是常数阵列对某个0<α ≤ 2满足(1)式。设bn=n1α(log n)1γ,这里γ > 0,当1< α≤ 2时,EX=0。若则(2)式成立。
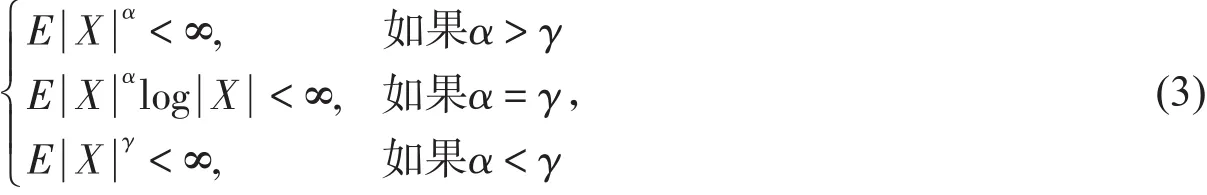
设{Xn,n≥ 1}是一随机变量序列且an>0,bn>0,q>0。若对任意ε>0,有

其中x+=max(0,x),(x)=(x+)q。这是Chow在文献[4]中给出的矩完全收敛的概念,显然矩完全收敛性蕴含完全收敛性。
本文在相同的条件下深化定理2,从完全收敛性进一步研究矩完全收敛并得到更好的结论,且本文运用不同于Sung[3]所用的方法使得证明过程简化。下面先介绍文章中出现的记号,在不同的地方正数C表示不同的值;log x=lnmax(e,x),e为自然常数;I(A)表示A的示性函数;an<<bn表示存在常数C>0,使得对足够大的n,有an≤Cbn。称随机变量阵列{Xni,i≥1,n≥1}尾概率有界于随机变量X,若存在一个正数C,对任意x≥ 0,i≥ 1和n≥ 1使得P(|Xni|> x)≤ CP(|X|> x)。
下面的引理给出了尾概率有界的随机变量阵列的矩不等式,这些不等式是由Adler等[5-6]创建的。
引理1设{Xn,n≥1}尾概率有界于随机变量X,则对任意n≥1,p>0,x>0,

由Hoffmann-Jφrgensen型不等式,Marcinkiewicz-Zygmund型不等式和截尾的方法,文献[7]建立了行为NA随机变量阵列加权和的矩完全收敛性的充分条件,不同于文献[3]中运用引理[8]建立的行为NA随机变量阵列加权和的完全收敛性的充分条件,使得证明过程简化。
引理2设{Yni,1≤i≤kn,n≥1}是行为NA的随机变量阵列,{kn,n≥1}是正整数序列,{an,n≥1}是正数序列,满足q>0且

(ii)存在0<r≤2和s>q/r,使得
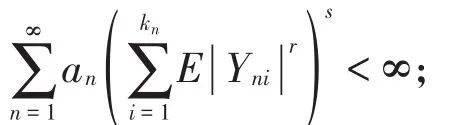

引理3设X是一个随机变量,γ>0,α>0,则
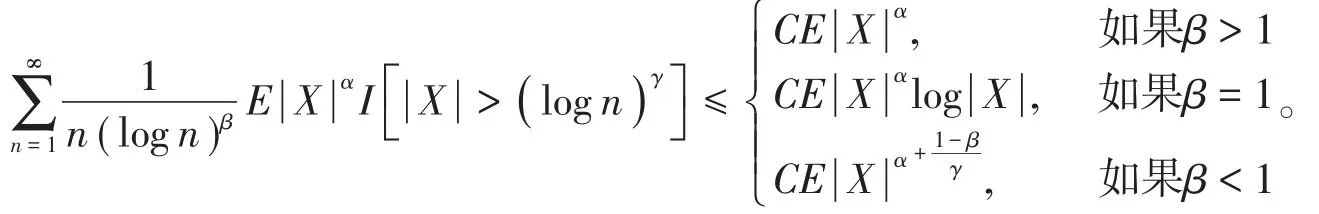
证明注意到

利用Fubini定理可得


下面给出本文的主要结论。
定理3设{Xni,1≤i≤n,n≥1}是行为NA的随机变量阵列尾概率有界于随机变量X,{αni,1≤ i≤ n,n≥1}是常数阵列对某个0<α≤ 2满足(1)式,令bn=n1α(log n)1γ,其中γ>0。当1<α≤ 2时,EXni=0,1≤ i≤ n,n≥ 1。若(3)式成立,则

证明不失一般性,可设ani> 0,1≤ i≤ n,n≥ 1(否则,可分别用和替代 ani,记 ani=-)。此处不同于文献[3]中分|ani|≤1或|ani|>1两种情形考虑。在引理2中取an=1/n,kn=n,r=α,Yni=aniXni/bn,1≤ i≤ n,n≥ 1。由ani> 0可知{Ynι,1≤ i≤ n,n≥ 1}仍是行为NA的随机变量阵。由(1)式不妨设≤ n,注意到q≤ α,则通过引理1、引理3得
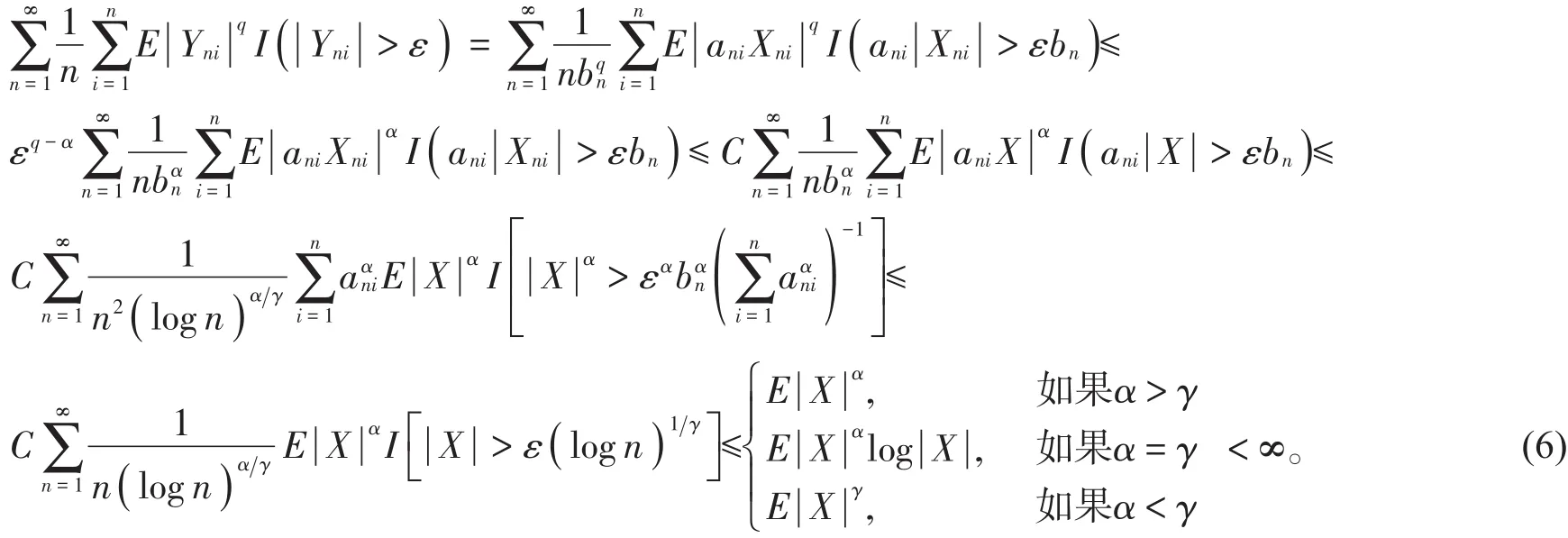
通过(3)式可得E|X|α< ∞,则对任意1≤ i≤ n,n≥ 1,由引理1可得E|Xni|α≤ CE|X|α≤ C。选择足够大的s使sα/γ > 1,s> q/α,有

当0<α≤1时,由E|X|α<∞、马尔科夫不等式及引理1,可得
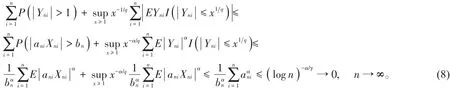
当1< α≤ 2时,注意到EXni=0,E|X|α< ∞,由马尔科夫不等式及引理1,有
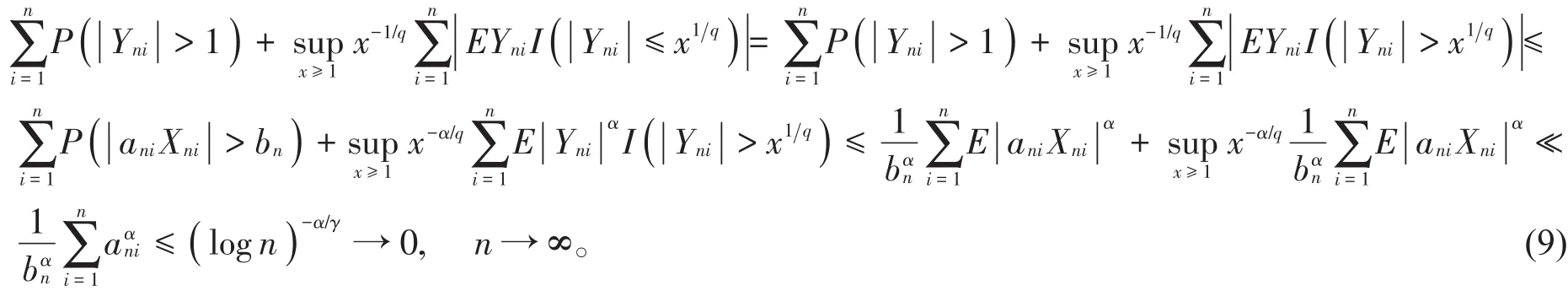
由(6)~(9)式可知引理2中的(i),(ii)和(iii)成立,从而(5)式得证。
注 由于矩完全收敛性蕴含完全收敛性,即(3)式蕴含(5)式。因此,在同样的条件下得到了文献[3]的结果,而且本文运用截尾的思想贯穿始终使得证明过程得到了极大的简化。
定理4设{Xni,1≤i≤n,n≥1}是行为NA的随机变量阵列尾概率有界于随机变量X,{αni,1≤ i≤ n,n≥ 1}是常数阵列对某个0< α≤ 2满足(1)式,设q> α,令bn=n1α(log n)1γ,其中γ> 0。当1< α≤ 2时,EXni=0,1≤ i≤ n,n≥ 1。若
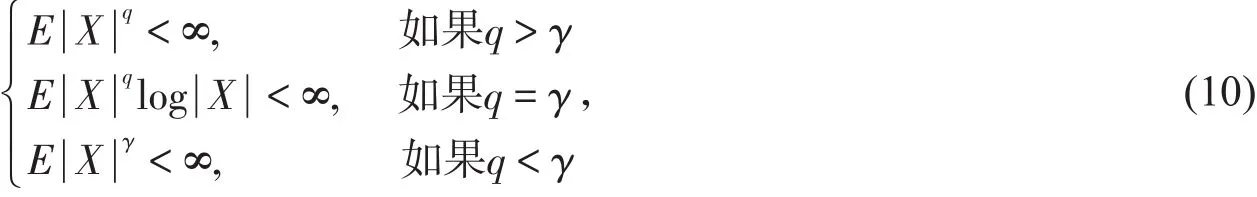
则
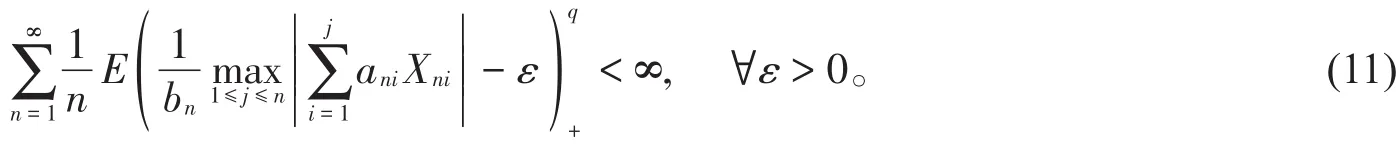
证明应用与证明定理3相同的步骤和方法,下面只给出过程不同的部分。注意到|a≤ n可得|ani|≤ n1α,1≤ i≤ n。因此,对任意q> α,有
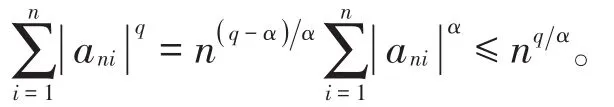
接下来,由引理1和引理3及(11)式,有
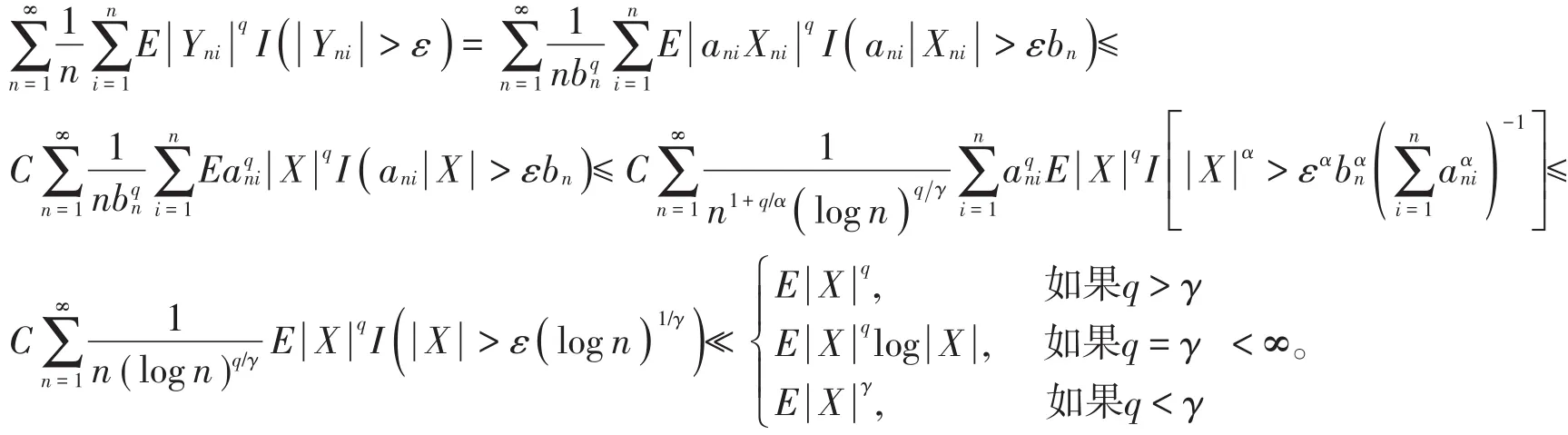
从q> α可知(10)式蕴含E|X|α< ∞,则(7)~(9)式依然成立,证明完毕。
