土石坝溃坝洪水分析：原理和计算程序

陈祖煜，陈淑婧，王 琳，张 强

(1. 中国水利水电科学研究院, 北京 100048；2. 全国市长研修学院, 北京 100029；3. 西安理工大学 水利水电学院, 陕西 西安 710048)

土石坝溃决洪水分析是预警和应急抢险工作中非常重要的基础工作，溃坝流量预测的准确与否可直接影响应急处置方案的制定与实施。这一分析工作涉及对非恒定高速急变流、泥沙动力学和岩土力学多领域耦合的模拟过程。过去50 a来，许多学者研究开发基于物理机制的溃坝模型。但是由于其本身包涵的复杂问题以及缺乏较多工程案例验证的原因，尚有待继续努力，以形成一门完善、成熟的学科分枝。

中国水利水电科学研究院在唐家山堰塞湖成功引流除险后，根据实测资料开展了反演分析。在此基础上对现有的溃坝洪水分析模型进行了改进。相应的研究成果发表于美国ASCE J. Hydraulic Engineering[1]。 随后，开发了溃坝洪水分析DB-IWHR。这一程序在Excel界面上开发，利用其强大的计算功能并结合VBA自主进行开发，形成具有一定创新性的计算溃坝洪水过程线的电子计算表格，是一个面向一线工程技术人员的实用软件。课题组又对易贡、小岗剑、板桥、白格等具有实测资料的堰塞湖溃决实例进行了分析[2-5]，已在我国水利水电行业获得了初步应用。鉴于相关的研究论文多为英文，本文综合前期的研究工作的要点，并对一些细节做进一步的说明，以供国内用户参考。

1 基本原理

1.1 溃坝水力学计算基础

溃口断面的流量可用宽顶堰公式计算。

(1)

(2)

式中：mb,mq分别为宽顶堰的流量系数和侧收缩系数。C为综合流量系数，理论值为1.7 m1/2/s[6]，可在1.3到1.7范围内选取[7]。H和z分别为库水位和渠底高程，m。见图1。

水流经过堰口跌落后水深为h，DB-IWHR采用简化处理方案。建议在0.8(0.6之间假定一个跌落系数：

(3)

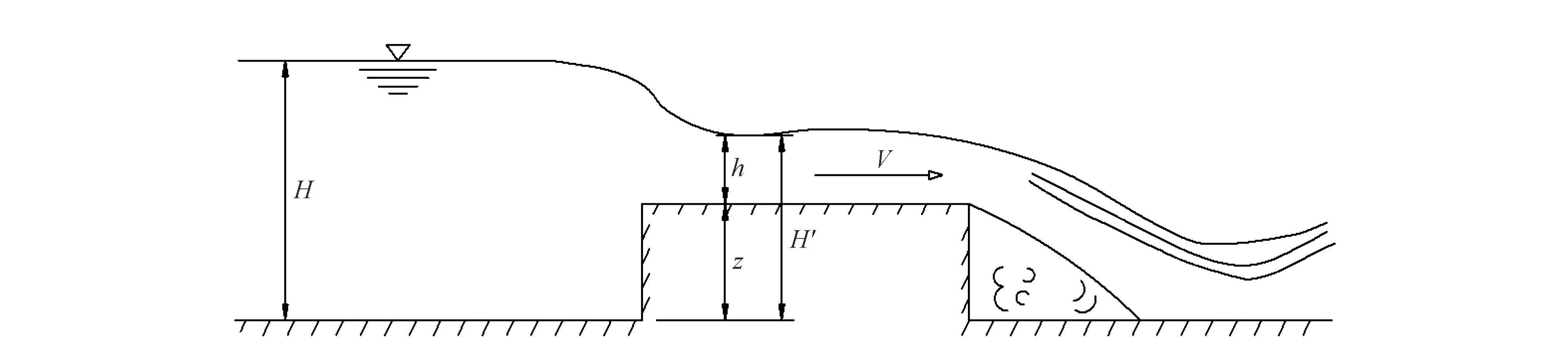
图1 宽顶堰泄流示意图

式中：h为溃口水深，m。可以通过敏感性分析考察不同的m值对计算结果的影响。经验表明，m的假定值对洪峰的计算值影响很小。

溃口断面流速V可按式(4)确定：

(4)

溃口流量可以通过单位时间内水库库容的损失来确定，因此：

(5)

式中：q为入库流量。

1.2 冲刷模型

DB-IWHR建议了一个双曲线模型，其形式如式(6)：

(6)

式中：v为扣除临界剪应力后的剪应力。

v=k(τ-τc)

(7)

双曲线有一当v接近无限值时的渐近线，其值为1/b，代表“可能最大冲刷速率”。此处，k取100，1/a表示v等于0时曲线的斜率。该模型基于结构材料的理解而建立的，即土体材料抵抗侵蚀时，不应有无限“强度”。 表1提供相应的参考值。

表1 双曲线冲刷模型参数参考值

计算冲刷速率需要确定剪应力，可按式(8)：

(8)

式中：γ为水的重度；R为水力半径；S为能坡。

1.3 溃口侧向扩展模型

溃口底部不断地被刷深的过程中，两侧边坡发生崩塌失稳，侧面不断地扩大。以前的溃坝分析模型采用楔形体法[8-10]，这一做法过于简单，水科院团队采用了岩土工程中已经被广泛接受的圆弧滑动面分析方法，并且比较合理地模拟了由于坡角下切导致的岩坡崩塌过程。相关的分析成果形成如图2(a)所示阶梯式溃决模式。但是在实际操作时，需输入每一步的圆心坐标、半径和渠底坐标，过于繁杂。在实际应用时，仍将计算获得的图形简化为一系列梯形，图2(b)示。

近期的研究表明，在可接受的精度范围内，可用一个双曲线模型来计算梯形侧面倾角增量Δβ，使用以下公式即可确定。

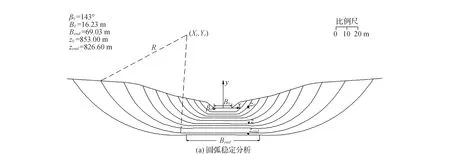
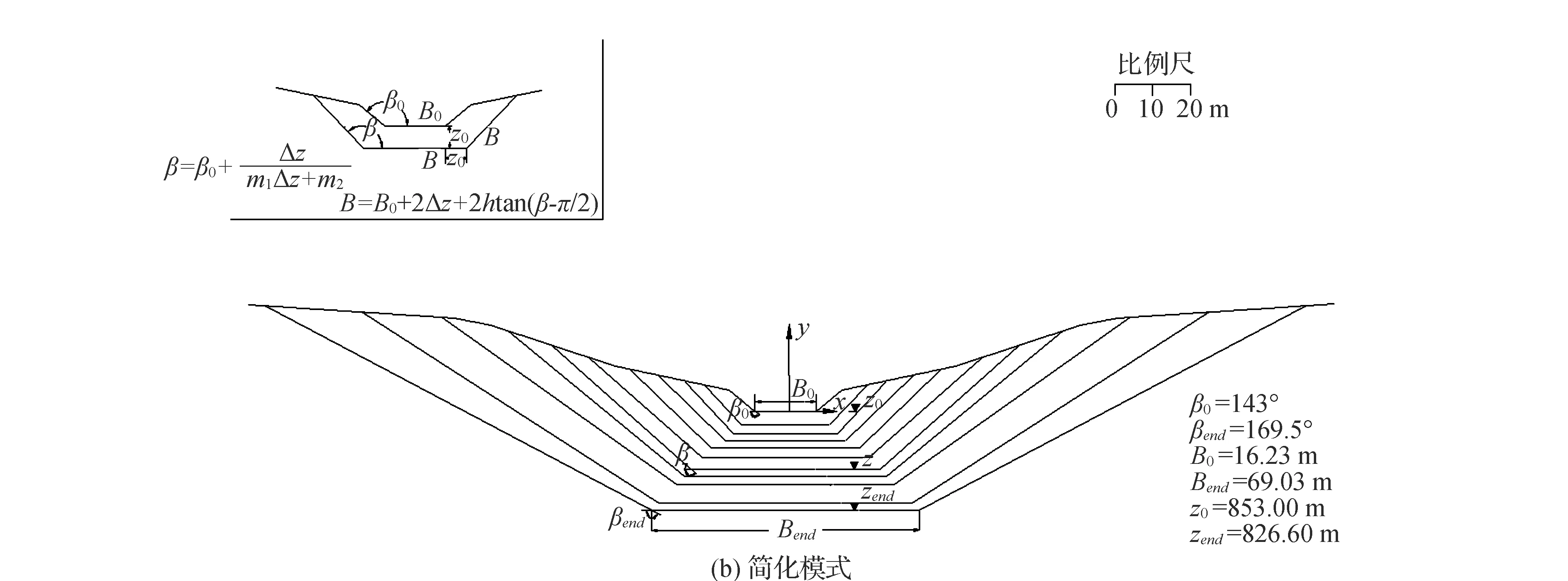
图2 溃口的侧向崩塌过程等效简化

(9)

(10)

式中：1/m1和1/m2分别表示双曲线的初始切线和渐近线。文献[11]提供了相应的图表以确定此两个参数。在更新DB-IWHR程序时，我们还进一步拟合了如图3和图4所示的线性关系。根据不同坝体土料的材料重度γ和强度参数内聚力c和内摩擦角φ，通过内插得到双曲线模型参数m1和m2。经验表明，凝聚力c对m2的数值影响不大。故图4仅依据摩擦系数tanφ来确定m2。

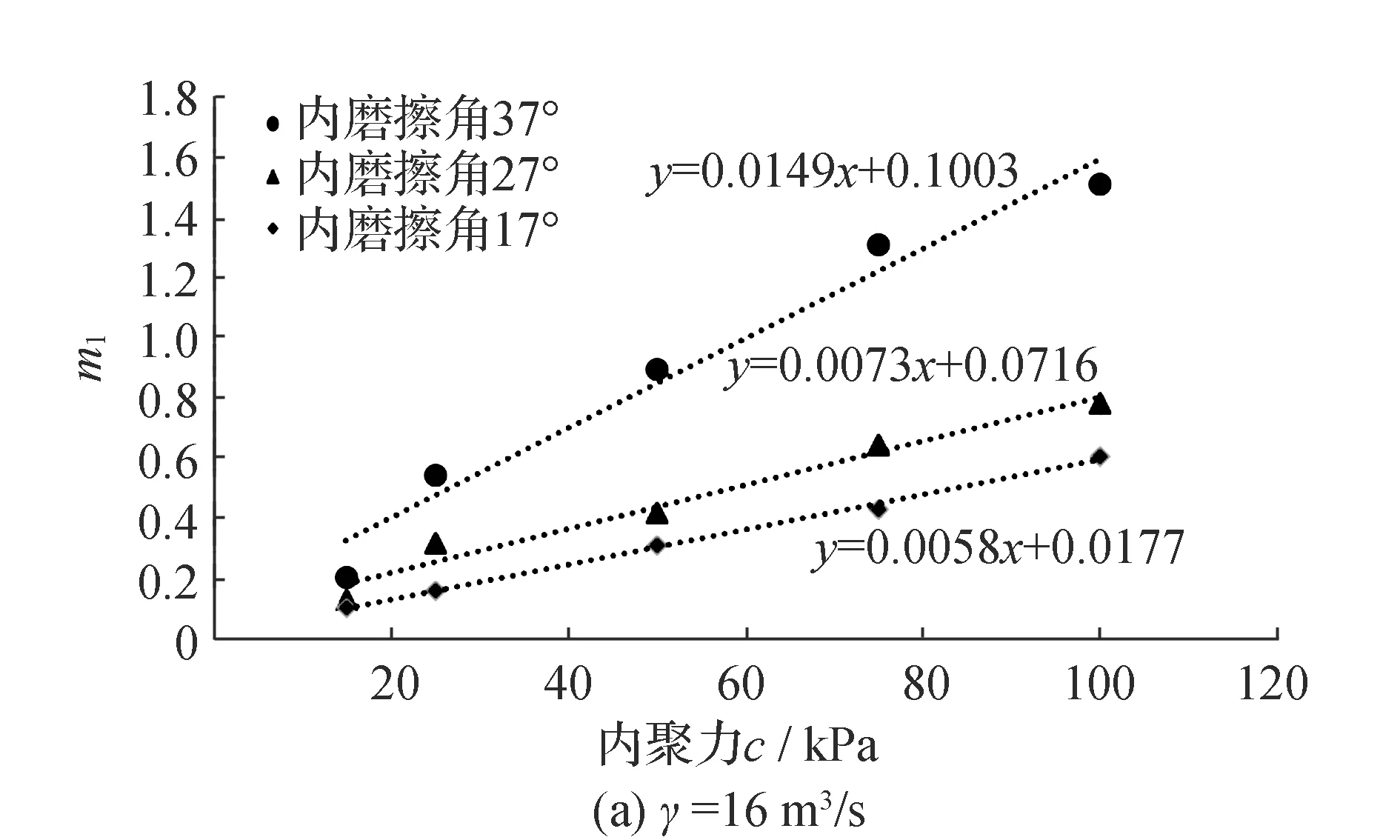
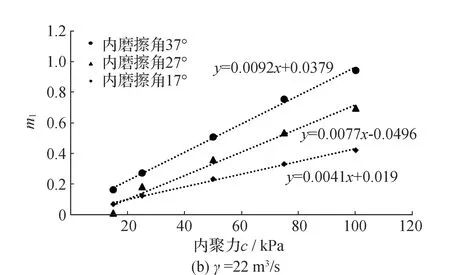
图3 经验系数m1的回归方程

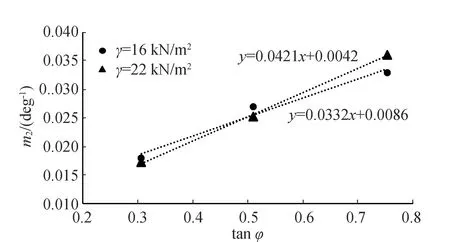
图4 经验系数m2的回归方程

2 数值计算方法

常规的计算方法[8-9,12]都是通过给定的初始时间t0和时间步长Δt，计算相应的水位增量ΔH，冲刷深度Δz和流速变化量ΔV。相应的算法是高度非线性的。计算程序包含复杂的迭代求解过程，常会遇见收敛困难。通过观察发现，一旦给定流速V，可以直接求出相应的ΔH、Δz和Δt。因此新的算法采用给定初始流速V0和流速增量ΔV。

DB-IWHR2018是在Microsoft Excel 2007中用VBA语言编写的程序，该程序能快速计算出大坝溃决的峰值流量。程序可在下面网站下载：

http://www.geoeng.iwhr.com/ytgcyjs/czy/zlxz/kbfx/A54160106index_1.htm.

3 溃坝洪水分析程序

3.1 程序界面

DB-IWHR包括主界面“Calculation”和库容水位关系计算“W-H curve”。近期，作者增加了一个引导界面，用于初学者在一系列提示下输入十余个参数(多数可取默认值)，迅速进入主界面计算。

DB-IWHR 2018需要输入表2中有关地形地貌、水力学和岩土力学参数。

图6所示唐家山堰塞湖溃决洪水计算界面。

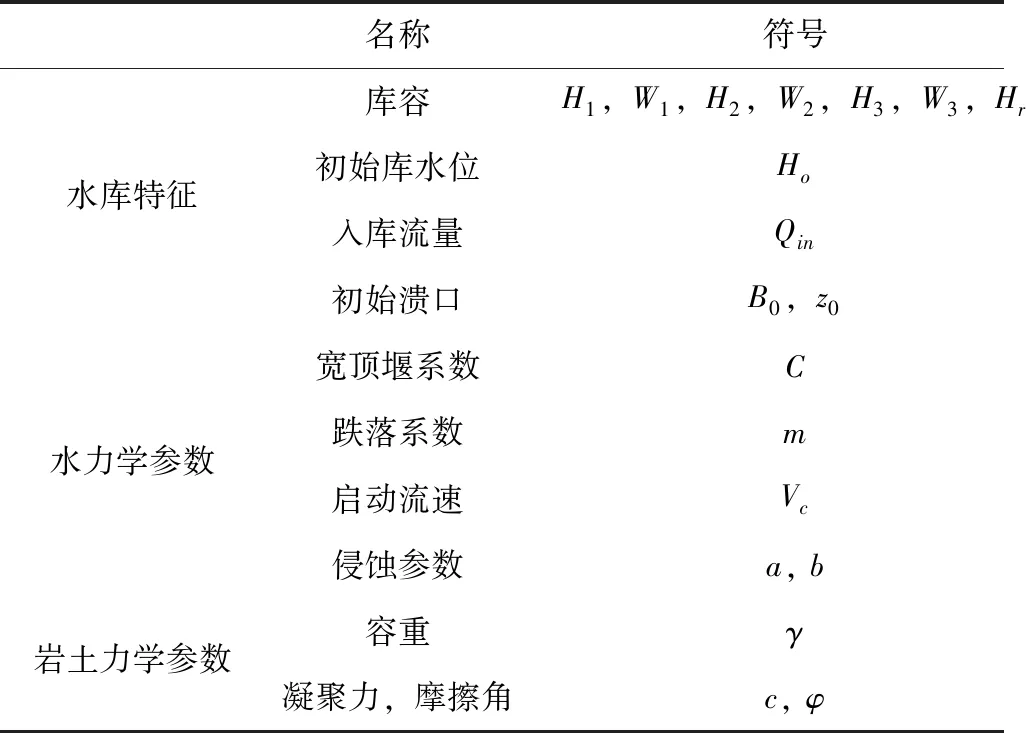
表 2 DB-IWHR需要输入的参数列表

4.2 成果分析

有关唐家山堰塞湖溃决洪水计算成果分析，已在文献[1]中详细讨论。总体的结论是，表2中侵蚀参数a,b是影响洪峰计算值最敏感的参数，需要在实践中不断摸索，深化认识。

(1)对淹没系数计算方法的改进。Fread[8]在BREACH模型中建议溃口水深计算可按明渠均匀流计算，即：

(11)

式中：n为曼宁系数；B为溃口宽度；J为下游坡坡比。在使用此式和相关的Breach程序时，需要输入下游坡坡比J的数值。图7是输入不同的J值获得的洪水过程，可见，J值对计算成果极为敏感。下游坡比J从0.05升高到0.24，溃口峰值流量增大24倍。

为分析相关参数对计算结果的影响，DB-IWHR模型计算中对上述曼宁公式做了进一步的推导，提出使用一个跌落系数m简化溃口水深计算，具体推到公式如下：

(12)

(13)

由上式(13)可知系数m具有一定的物理意义，即为水流从水库至溃口处水头跌落，故定义为跌落系数。文献[1]的敏感性分析也考察不同的m值对计算结果的影响，结果表明，m的假定值对洪峰的计算值影响很小。因此，DB-IWHR不使用式(13),而是建议直接为m提供一个默认值，如0.8。用户可对其作敏感性分析，考察不同的m是否确实对计算成果影响不大。

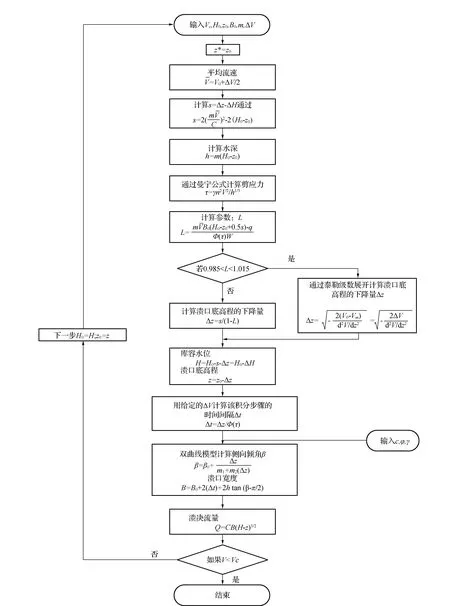
图5 数值分析方法的流程表

图6 DB-IWHR2018程序界面

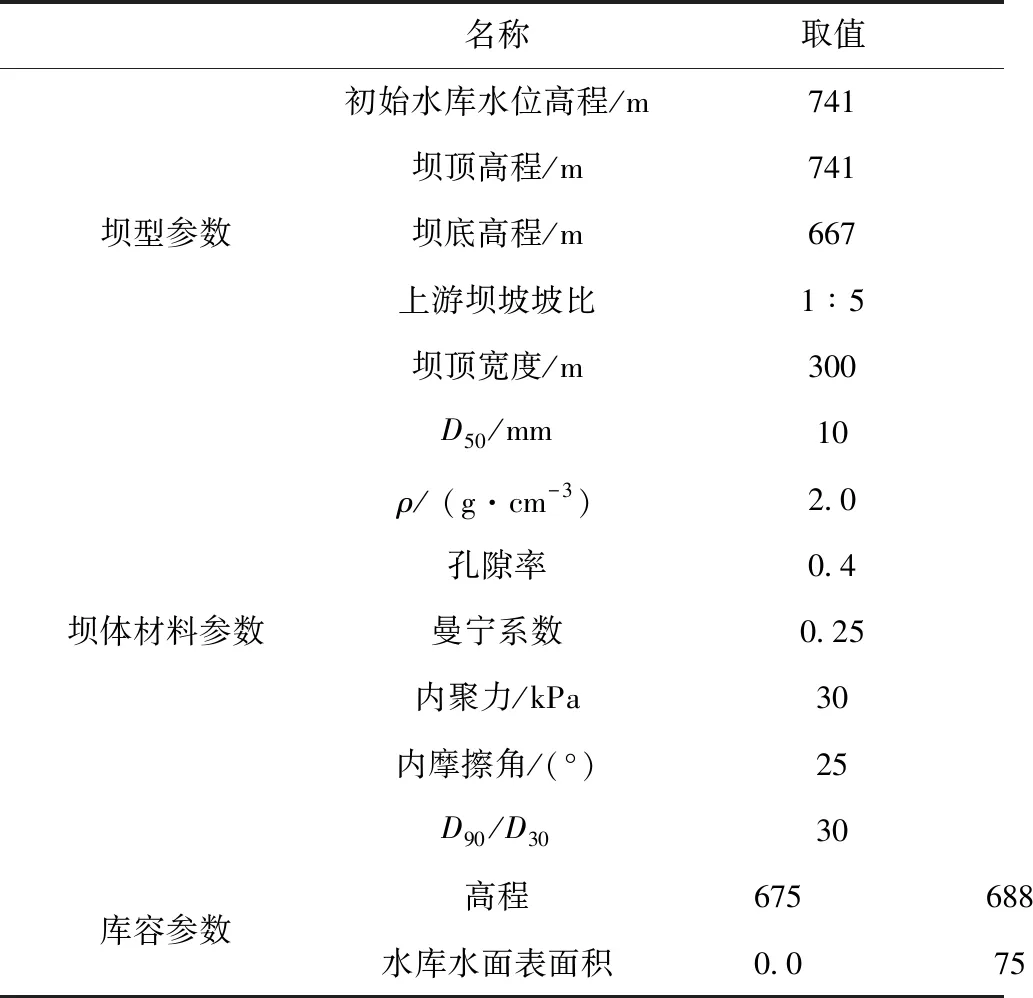
表3 BREACH 模型模拟唐家山堰塞湖溃决流量的输入参数

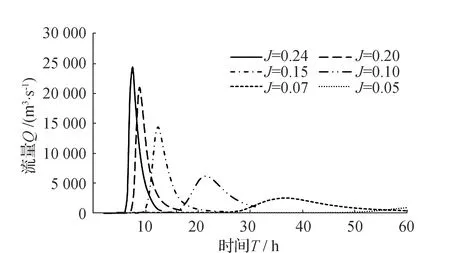
图7 BREACH模型中下游坡比J的敏感性分析结果(输入参数见表3)

(2)双曲线模型和线性模型的比较。文献[1]根据实测冲刷率数据，采用双曲线冲刷模型进行拟合，以计算唐家山堰塞湖在溃决过程中的冲刷速率，溃决流量的计算结果显示双曲线模型参数大范围变动对流量计算结果不很敏感，并且，也发现双曲线模型对计算成果十分敏感。本文进一步论证线性冲刷模型对计算成果同样十分敏感，不宜直接在溃坝洪水分析中应用。

线性模型具体形式如下：

(14)

式中：a1是线性冲刷系数。唐家山堰塞湖实测冲刷率的线性回归结果如图8(a)所示，对应图中a1分别取0.1,0.2,0.3时，溃决流量曲线如图8(b)所示，峰值流量依次为4219 m3/s，9024 m3/s，14 723 m3/s。计算结果说明线性模型系数小幅度变化时对计算峰值流量的影响却很大，因此若采用线性模型增加了合理选取参数的难度，从而降低了溃坝流量模型计算结果的可靠性。

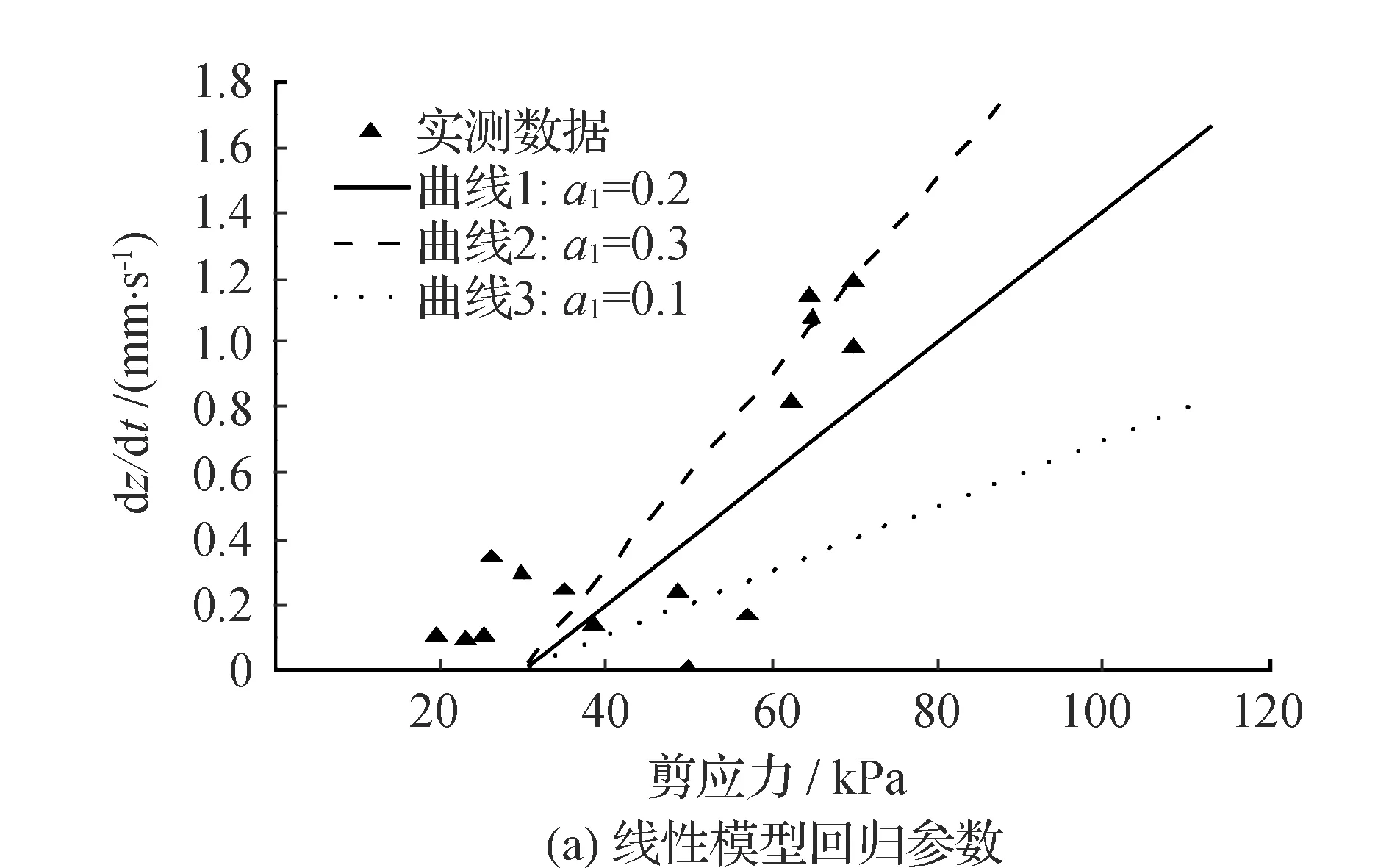
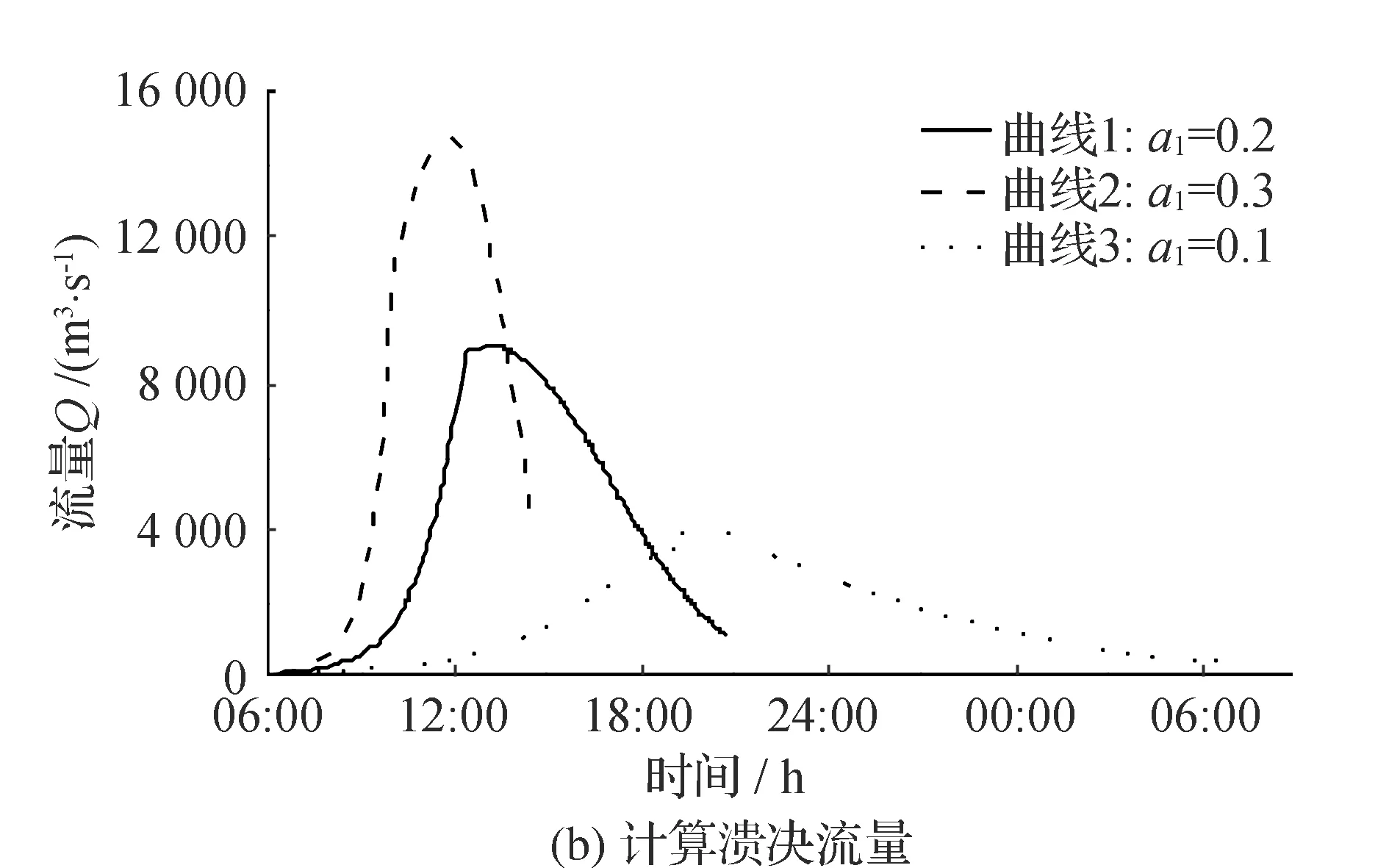
图8 线性模型参数敏感性分析结果

4 结 论

本文介绍中国水利水电科学研究院近期对土石坝溃决洪水分析方法的改进以及相应的软件开发工作。对数值分析方法的改进主要为以下方面：

(1)提出了一个描述土体冲刷的双曲线模型。此模型的两个参数具有物理意义。参数1/a代表起动区冲刷速率依线性关系相对剪应力的比例系数，可在实验室内测定。参数1/b代表在高流速区冲刷速率逼近“可能最大”的渐近值。表2提供了参考值。随着经验的积累，这些参考值可不断更新。这一模型可以使计算的稳定性大大提高，不会出现因输入参数微小变化导致洪峰值急剧变动的现象。

(2)对于溃口侧向崩塌扩展也提出了一个经验的双曲线模型。可以根据土体的容重、凝聚力和摩擦角确定相应的参数m1和m2。

(3)提出了一个以速度增量为基础的数值积分模式，回避了非线性迭代，使全部计算线性化。

在上述改进的基础上开发了溃坝洪水分析程序DB-IWHR具有以下特点：

(1)程序是在Excel界面上开发的计算表格。使用者只需在引导表格输入15个参数。其友好的界面使绝大多数用户不需要接受过于繁复的培训，即可开展计算工作。

(2)鉴于其线性化的处理，计算过程快速，鲁棒性强。

(3)全部计算过程开源，透明。便于校核和二次开发。