基于教材习题的微专题教学设计

江苏省苏州市吴县中学 (215151)

康小峰

微专题是高三数学二轮复习的常见形式，一般是通过一两节课的教学就某类热点问题让学生形成解决一类问题的思维主线，从而达到提升学生解题能力的效果.但纵观时下的高三数学二轮教学现状，很多老师在操作上还存在以下误区：1.专题不专，大多数专题还是以知识点分类的，内容多而杂，并未聚焦在核心问题和热点问题上；2.教法单一，课堂上多半是以教师讲解和展示学生解题过程为主，学生缺乏深度思维，课堂索然无味，从而导致学生学习效率低下.另外，通过浏览近几年的各地模考卷和高考试卷，笔者发现很多试题源于教材又高于教材，这说明教材上的习题大多具有丰富的背景和广阔的外延，值得教师进行二次开发，如能以此为载体进行探究形成一系列微专题定会收到意想不到的效果.基于以上教学现状和思考，笔者试图从发展学生数学核心素养的角度进行了一些探索和尝试，现就如何以教材习题为题根进行微专题设计谈谈自己的想法，不当之处，请同行批评指正.

一、由习题渗透思想方法

我们知道数学思想方法是数学知识的重要组成部分，但它又较数学知识具有更高的层次，它是一种数学意识，可以用来指导我们的解题,是一种重要的素养.因此，要让学生自觉形成用数学思想方法来指导解题，就必须在平时的教学中加以渗透，仅仅靠几个思想方法专题是无法将其内化为学生的自觉行为，而课本中一些简单的习题，如能合理利用并加以变式，定能给学生形成强烈的脑风暴.这里以苏教版必修5第106页第17题为例作简要的探讨.

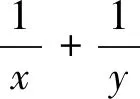
分析：教材中的这道题是一道经典的利用基本不等式求最值题，经过一轮的复习学生已经掌握两种常见求解方法.

(方法一)利用消元法，转化为求一元函数的最值(过程略).

方法二是借助“整式和”与“分式和”的关系，利用一次基本不等式达到求最值的目的，且“整式和”与“分式和”两个整体只要知“一”便可求“一”.它是很多类似问题的题根.为便于说明，笔者借助下列变式加深对此类问题的理解.

分析：本题仍属“整式和”与“分式和”关系的问题，对比题根发现，本题分式和的两个分母较题根复杂，写成了两项和的形式，通过换元即可化归为基本类型.

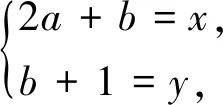
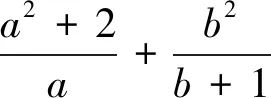
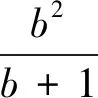
分析：本题条件以不等式形式出现，咋一看难度很大，若将其改为x+y=2,即化归为变式2，再还原成不等式，利用不等式的传递性，即可求解.

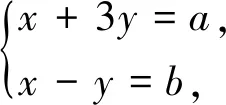
上述教学设计片段是基于课本中的一道习题展开的，通过再现其常见的处理方法，迅速将学生的思维拉进“1”的代换这一配凑技巧，然后笔者遵循低起点、层层递进的原则，设计了一系列变式题，引导学生解决这类问题要时时刻刻做到对题根的回头看并及时消除解题差异，通过对条件和目标函数的转化，化归为基本类型，这样的历练过程对学生的思维无疑是有益的，远比对着题目说本题考察了转化和化归的数学思想效果更好.因此，数学思想方法的渗透并不是直接告知的，而是在潜移默化中感受和形成的.

2.由习题优化解题方法

高考答题的最高境界是既快又准，也就是要优化解答，这除了靠平时的大量刷题外，还要进行解题反思，做好题目的归类和小结.不妨让我们把视线转向教材，教材中的很多习题看似平淡无味，但如果认真研究便可衍生出许多有用的结论，利用这些结论便可秒杀各类考题.下面笔者以苏教版必修4第89页第12题为例进行说明.

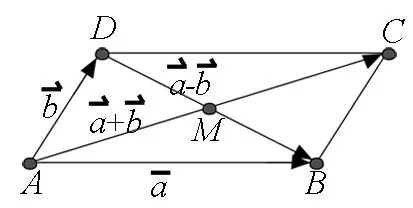
图1

本题的证明非常简单，其几何意义也是大家非常熟悉的(平行四边形对角线的平方和等于四边的平方和).利用几何意义证明更加直观：

问题1如将上述①②两式相减你会有怎样的发现？

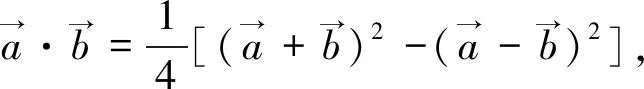
问题2你能给出极化恒等式的几何解释吗？

问题3特别地，如将平行四边形ABCD退化成ΔABD，你又能得出怎样的结论，能给出几何解释吗？

问题4你觉得使用该结论的关键是什么？

两向量共起点是关键.

图2 图3

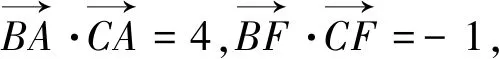
图4

分析：由D是BC的中点并结合三个数量积的形式，直接可由极化恒等式切入得

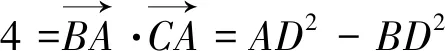
上述教学设计是在一道简单习题从“数”与“形”两方面解决之后展开的，教师通过问题串的形式引导学生由浅入深进行探究，旨在培养学生发现和分析问题的能力.得出极化恒等式后教师并未急于进入例题讲解，而是让学生尝试用自己的语言给出其几何解释，在大脑中先留下直观的印象，为后续解题时进行模式识别做好准备.几个例题梯度明显，给出了不同背景下的公式运用，通过分析与求解使学生认识到向量数量积的求解除了常规的基底法和坐标法外，极化恒等式也是求解数量积的不二选择，很多时候可“秒杀”一类模考和高考向量试题.整个设计并不是向学生灌输高难度的解题技巧，而是教会学生如何选择解题工具，如何理解数学问题的本质，从而有效地培养了学生的数学运算、直观想象和逻辑推理等数学素养.

3.由习题渗透数学文化

《普通高中数学课程标准》明确指出：在高中数学课程的教学活动中，应当有意识的结合相应的教学内容，引导学生了解数学与人类发展的相互作用，体会数学的科学价值、人文价值和应用价值；在寻求数学发展历史轨迹的过程中，激发学生数学创新的动力，提升学生的文化素养和科学精神.苏教版《数学》教科书非常重视数学文化，在章首语、正文、阅读材料、习题中均有体现.因此，在平时的教学过程中，我们可以以教材中的习题为载体，适时的向学生渗透数学文化，使学生在数学学习过程中体验数学文化的魅力，促进学生核心素养的发展.接下来以苏教版选修2-1第64页练习4为例进行阐述.

例6 (题根)求平面内到两定点(-2，0)，(1,0)的距离比等于2的动点M的轨迹方程.

问题1你能指出M点的轨迹吗？

点M的轨迹是以(2,0)为圆心，2为半径的圆.

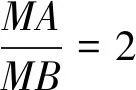
点M的轨迹仍然是圆.

问题3根据上述问题，你能将例6推广成更加一般性的结论吗？

类比问题1的解题方法进行求解.

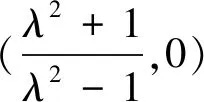
上面这个圆就是大名鼎鼎的阿波罗尼斯圆，它是公元前3世纪，古希腊数学家阿波罗尼斯在研究众多平面轨迹问题时所发现的，简称阿氏圆，这个著名结果被收录在《平面轨迹》一书中.阿波罗尼斯与欧几里得和阿基米德齐名，他的著作《圆锥曲线论》是古代世界光辉的科学成果，它将圆锥曲线的性质网罗殆尽.

我们知道阿氏圆涉及的要素有定点A、定点B、动点P到两定点的距离之比及动点P的轨迹方程，刚刚我们由前三个要素求出了第四个要素，那么如果已知其中任意三个量能求出第四个量吗？

问题5通过对阿氏圆四个要素的分析，类比问题4，你能给出其余的变式，并给予解答吗？

学生们很快给出了其余两种变式：

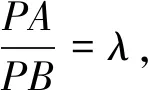
类比问题4的解题方法，学生们很快给出了解答,限于篇幅，这里就不做解答了.

上述教学设计是根据课本中的阿波罗尼斯圆问题延伸和拓展的，学生在建构阿波罗尼斯圆的同时，感受到了数学文化的熏陶，随后，通过一系列变式和探究活动，让学生加深了对阿氏圆本质的理解，同时学会了研究问题的一般方法，积累了数学活动经验,从而有效的促进了数学核心素养的提升.随着普通高中数学课程标准(2017年版)的出炉，数学的文化价值愈显重要，它不仅出现在教材的习题中，在高考试卷中的比重也会越来越高，因此，在平时的数学教学中，教师要有意识地对学生进行数学文化的渗透，它不仅可以帮助学生理解和记忆所学知识，也是提高学生文化修养、落实核心素养的一条重要途径.