基于心电信号提取呼吸信号的算法研究
2019-04-28蒋莲陈兆学
蒋莲,陈兆学
上海理工大学医疗器械与食品学院,上海200093
前 言
呼吸率是临床医学中常用的监护参数之一。目前应用于人体呼吸信号的检测方法主要分为两类:一种方法是利用温度、湿度或气流传感器直接检测法,通过检测从人体鼻部流入和流出肺部的气体得到人体呼吸波;另一种方法是利用阻抗式或压力传感器的间接检测法,通过检测由人体呼吸引起的人体胸部形变或胸部阻抗变化而获得呼吸波[1]。这两种方法都有其缺点,前一种方法受检位置在鼻部,会使受检者在检测时感到呼吸不适;后一种方法需要受检者在安静时进行测量,不能够长时间动态检测人体呼吸。诸多的临床资料证实,当人体呼吸时会导致心电图的波形发生变化。即心电信号波形的幅值变化与人体呼吸运动存在一定的联系,人体心电信号中包含呼吸信息[2],当人体呼吸时,胸腔部位节律性的收缩和扩张运动将使得描述心脏动作电位传播方向的心电轴也出现周期性的变化,从而导致心电信号波形的QRS 波呈现为周期性的波动[3]。在临床应用中,为了减少含有各种传感器的其它检测设备的使用和减少受检者的束缚,从人体心电信号中直接解析出呼吸信号信息显得尤为重要,它不仅使动态检测人体呼吸率成为可能,还是一种高效、低成本的呼吸率检测方法。
许多研究者基于对心电信号的处理和分析已经获得了呼吸信号。Wang等[4]提出基于心电波形变化的EDR(ECG-Derived Respiratory Signal)算法,基于心电向量图(Vector Cardiogram,VCG)提供了人体呼吸率和呼吸深度。Pinciroli等[5]和Moody等[6]提出基于心电电轴的分析法。Pilgram等[7]提出基于心率的EDR 方法,该方法需要对信号的R-R 间隔进行奇异值分解(Singular Value Decomposition,SVD),从而得到呼吸信号的频率。Ding 等[8]提出一种心电信号高阶统计量的计算方法,该方法需要检测出心电信号的R波,通过计算信号的高阶统计量来获取人体呼吸信息。Orphanidou 等[9]选用数据融合方法来获得呼吸信息,将心电信号R波峰值的振幅调制和呼吸性窦性心律失常两种方法融合在一起,从而达到了良好的呼吸信号提取效果。从心电信号中提取呼吸信号的算法虽然很多,但是各种处理算法存在优劣,有的算法计算速度快,但准确率并不高,有的算法计算准确率高,但受到心电信号数据量和计算复杂度的限制。因此,本文提出一种独立分量分析(ICA)的EDR方法。通过MATLAB 对算法进行验证,并将实验结果与其它研究结论相比较,经研究发现该算法能够从各种干扰中直接分离出呼吸信号,避免各种复杂滤波器的设计,且计算速度快,结果准确,是一种有效和可靠的EDR算法。
1 EDR算法
人体心电信号是非常微弱的信号,容易受到工频噪声干扰和呼吸运动的影响。因此,通过医用设备检测到的人体心电信号往往混有很强的背景噪声,最主要的3种干扰有:工频噪声干扰、肌电干扰和基线漂移[10]。其中基线漂移由于人体呼吸、胃肠蠕动以及导联电极的移动等低频干扰产生,表现为信号波形会随着基线出现漂移[11],它的频率很低,一般在1 Hz以下。而人体呼吸信号的频率一般为0.1~0.5 Hz,也分布在心电信号的低频部分。因此直接通过时频域方法提取呼吸信号会存在较大困难。ICA 方法是近年来由盲源分离技术发展而来的一种多维度信号统计处理方法,可以根据源信号的基本统计特征,由观测数据最终恢复出源信号[12]。因此,基于ICA方法寻找源信号的思想,关键部分是需要从原信号中提取出包含呼吸信息的混合矩阵,再运用ICA算法即可分离出呼吸信号。通过ICA方法的EDR算法流程如图1所示。
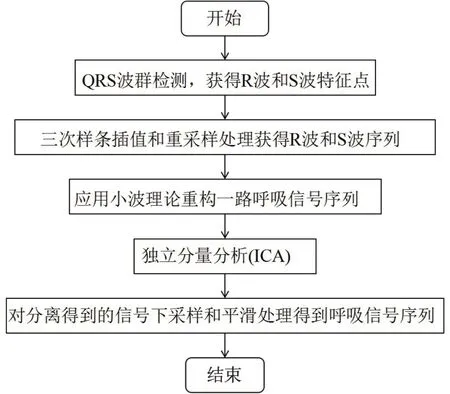
图1 EDR算法的流程图Fig.1 Flow chart of electrocardiogram-derived respiratory signal(EDR)algorithm
2 EDR算法的实现
本研究使用的是由动态心电图[13]检测到的不同人体的24 h 心电数据,采样频率为250 Hz。仿真验证时,将原始心电数据分成12 段,取每一段的1 min时间长度,共计15 000 个采样点的心电数据信息进行显示。为方便说明,本文仅以其中一段数据的1 min数据为例。
2.1 QRS波群检测
快速而准确检测出心电信号中QRS 波群的位置,是心电信号自动分析和诊断系统中的一个关键环节,各种算法层出不穷[14-16]。呼吸信号隐含在人体心电信号中,具体体现在:人体呼吸运动会引起心电信号特征点R波的幅值变化,还对R-R波间期存在一定的影响。基于这样的理论基础,需要从心电信号中提取出包含呼吸信号的R 波特征点和S 波特征点。本文采用Pan&Tompkins 算法检测信号的QRS波群,该方法具有原理简单、计算量较小和实时性好等优点[17]。其数据检测结果如图2所示。
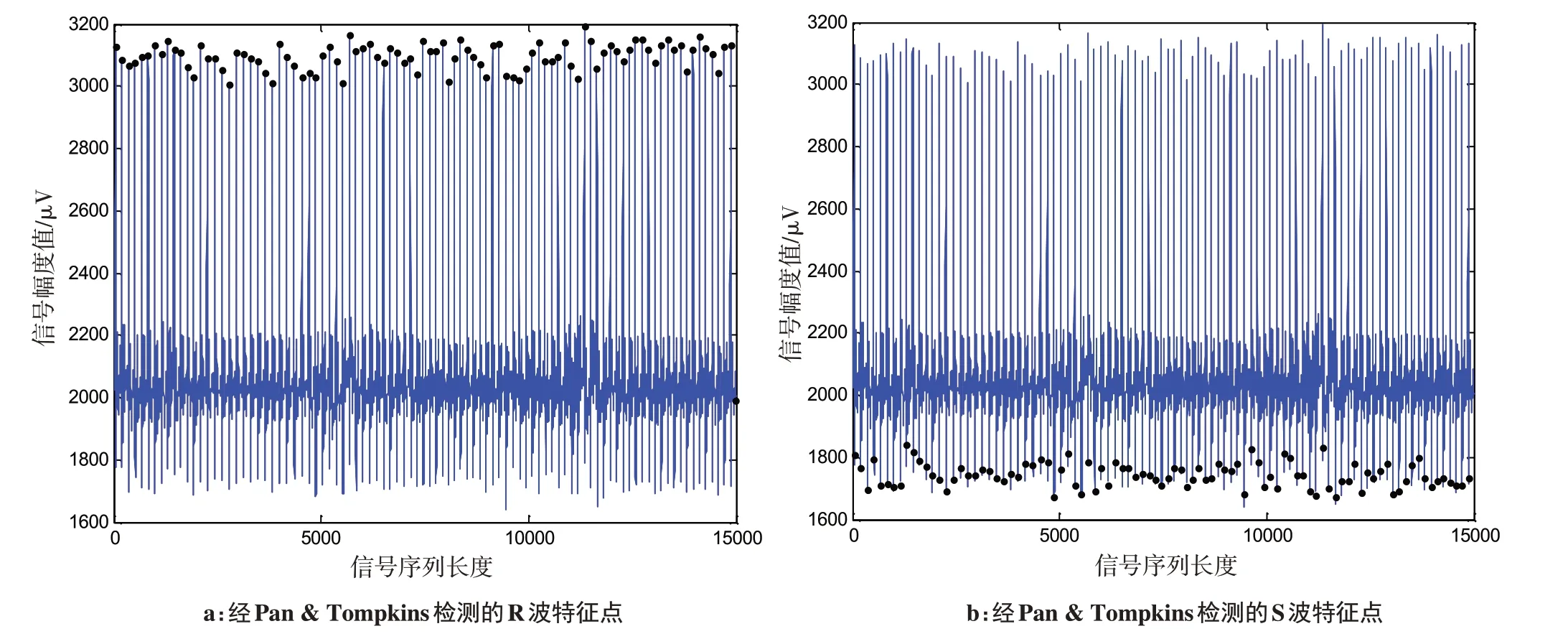
图2 经Pan&Tompkins算法检测到的R波和S波特征点Fig.2 Detected feature points of R wave and S wave by Pan&Tompkins algorithm
2.2 R波和S波特征点的三次样条函数插值和重采样处理
由于获得的R 波和S 波峰值及其索引值均为离散数据点,若要得到连续的包含R波和S波信息的数据序列,则需要对离散点进行插值。本文中选用了三次样条函数插值法[18]。三次样条函数插值法是基于一个特定的数据集合,如果给出n个给定点的数据,就可以利用这n个给定点将数据集合分为n-1段,用n-1 段三次多项式即可在每两个连续给定数据点之间构建一个三次样条[19]。三次样条插值算法的流程如下,设共有n个插值节点x1<x2<…<xn-1<xn,则经过数据点(x1,y1),(x2,y2),…(xn-1,yn-1),(xn,yn)的三次样条S(x)是一组三次多项式:

该多项式在节点处有连续性和在节点处的一阶导和二阶导有光滑性。根据边界条件可以求得ai、bi、ci以及di的值,从而求得Si(x)的表达式,进而得到拟合后的光滑曲线。经过插值拟合的两路信号如图3所示。
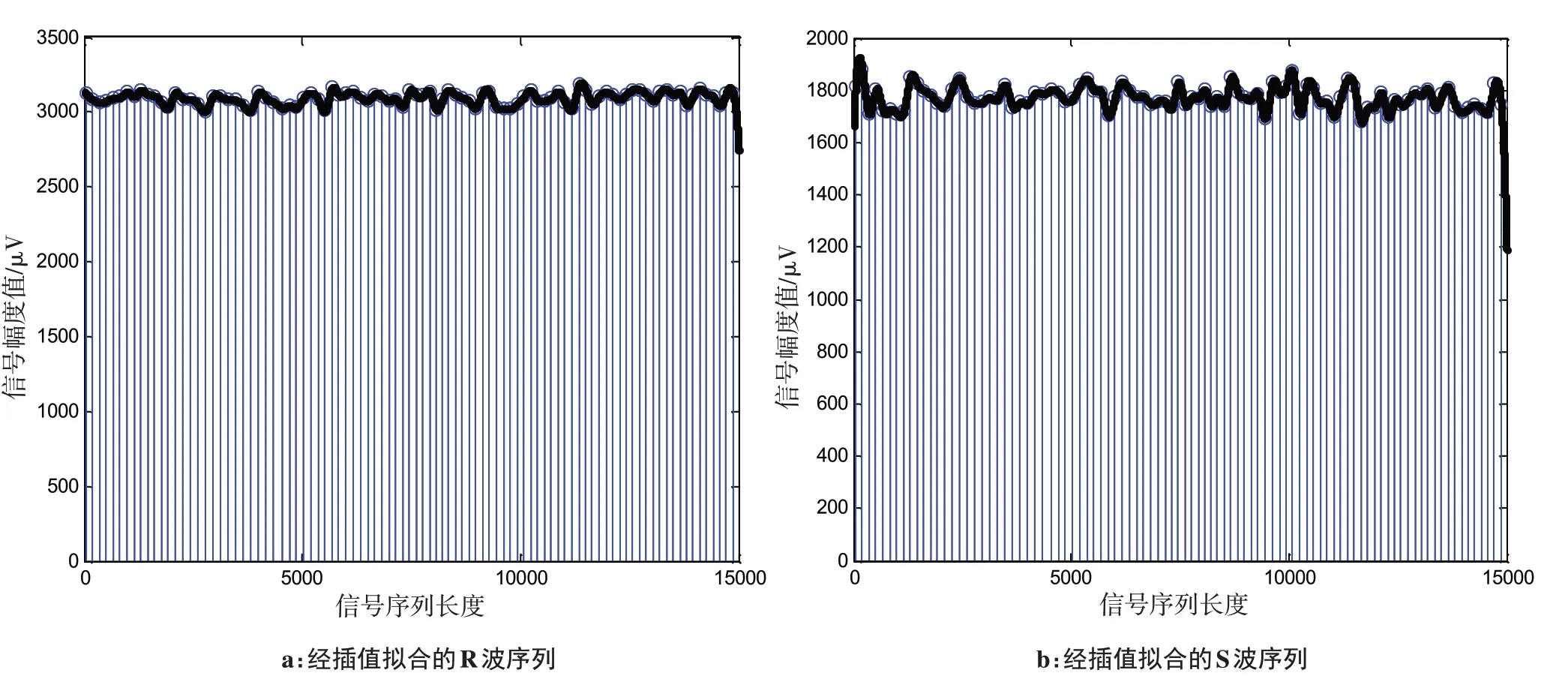
图3 经样条插值算法拟合的R波和S波序列Fig.3 R and S wave sequences fitted by spline interpolation
从心电信号的一个周期波形中可以看到,R波出现在S波的前面,故经检测到的R波和S波特征点在位置上会存在一定的延时。为了保持拟合后的R 波和S波序列的一致性,还需要对该两路序列进行重采样,从而获得在同一时刻点采样的两路信号序列。经过重采样的两路信号序列如图4所示。

图4 在同一位置重采样得到的R波和S波序列Fig.4 R and S wave sequences re-sampled at the same positions
2.3 应用小波理论重构一路呼吸信号
小波变换即是通过小波技术对原信号进行分解重构,主要包括空间(时间)和频率的局部变换,应用平移和伸缩运动等运算功能可实现信号或函数的多尺度的细化分析。当对信号进行一阶小波分解后,信号被解为两部分:近似信号A和细节信号D。其中,近似信号包含信号的低频成分,细节信号包含信号的高频成分[20]。当运用小波理论重构呼吸信号时,首先需要确定信号的分解层数。相关研究表明,在基于小波变换的心电信号频率分解和重建中,coif4小波基函数是心电信号数字滤波的最佳选择[21],其中,小波coif4函数的频率分解规则如表1所示。
本文使用的心电信号频率为250 Hz,而正常人体每小时的呼吸速率约20 次/min,换算成频率为0.2~0.5 Hz。参照表1中coif4 小波函数的频率分解规则,则需要进行9层频率分解才可得到呼吸信息所在频段。为了从心电信号中重构出一路呼吸信号,需要原信号频率作十次分解,从而得到十个细节分量值,通过保留第九层的小波分量,并把分解后信号的其它层次细节分量均置为零,再采用waverec小波函数对第九层细节分量进行重构就可得到一路呼吸信号序列,重构的呼吸信号序列如图5所示。
2.4 ICA算法理论
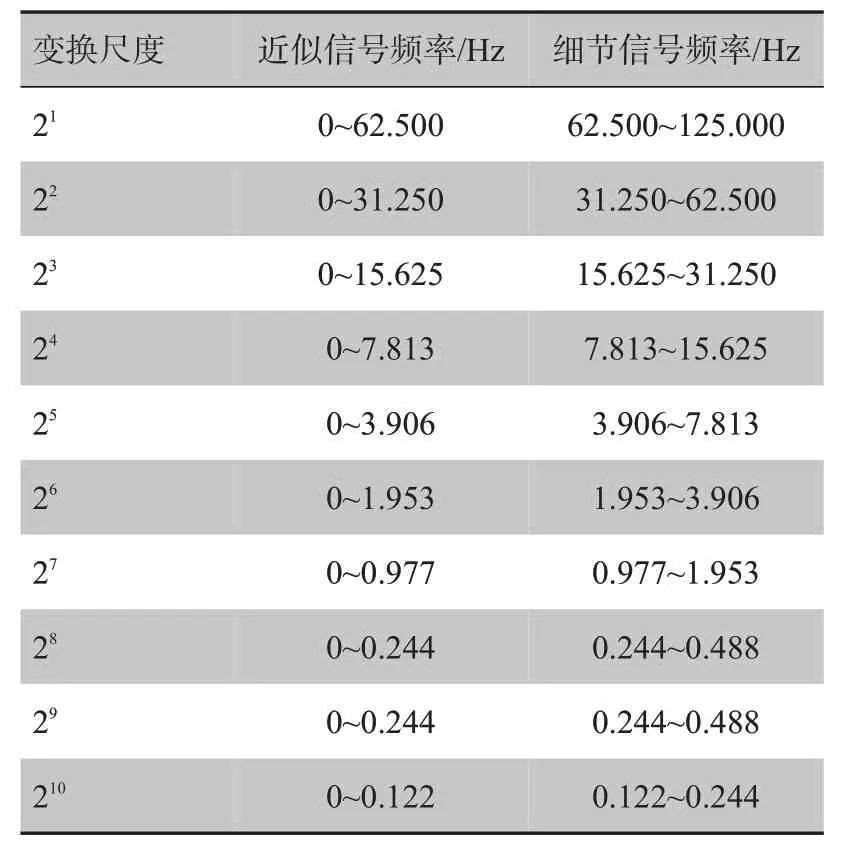
表1 coif4函数的频率分解规则Tab.1 Frequency decomposition rule of coif4 function
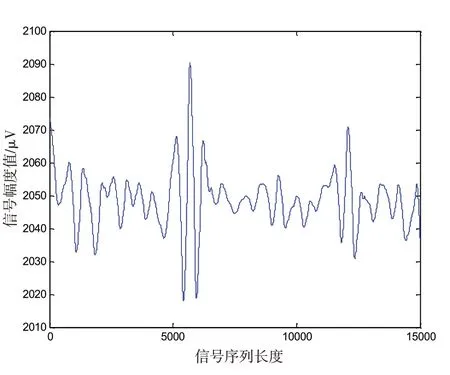
图5 重构的呼吸信号序列Fig.5 Reconstructed respiratory signal sequence
ICA是盲源分离领域的一项关键技术,它在没有任何先验知识的前提下就能从多个混合信号中提取或分离出源信号[22]。ICA问题的数学表达式为:

式中,s是n维源信号向量,s=[s1,s2,…sn] ;A是混合矩阵;x是m维观测的混合信号向量,x=[x1,x2,…xm]T;观测信号x为信源向量s的瞬时线性组合。
ICA 算法的实质是依据观测信号x和源信号s分量之间的统计独立性假设,根据源信号s在概率分布上的某些先验条件,最终估算出一个混合矩阵A。即通过求解出一个分离矩阵W,使得y=Wx的各分量尽可能保持统计独立,并把y看作为源信号s的估计。ICA的原理框图如图6所示。

图6 ICA的原理框图Fig.6 Principle diagram of independent component analysis
运用ICA模型进行信号分析时,需满足以下假设条件:(1)源信号s(t)各分量之间是统计独立的,即分量间是线性无关的,并且所有分量中最多一个信号满足高斯分布;(2)观测的混合信号个数要大于或等于源信号个数,即m >n;(3)混合矩阵A是列满秩的可逆矩阵。
目前,常用的ICA 算法大致可分为两大类:一类是基于随机梯度法的自适应算法,该算法可以通过神经网络实现,但是受选取的学习速率参数的影响,其运算收敛速度慢。另一类是基于批运算相关目标函数的快速算法,即FastICA[23],该算法主要是寻找一个方向使得WTx具有最大高斯性,主要采用了定点迭代的思想,其计算简单且具有较好的收敛性。因此,本文中选用了基于负熵的FastICA算法获取源信号序列。将经过插值和重采样分别得到的R 波序列和S波序列,利用小波函数分解和重构的一路呼吸信号以及现有的连续24 h 心电原始信号序列4 路信号混合,构成一个观测矩阵。选用基于负熵的FastICA 算法分离得到不同的独立源分量序列。经过ICA得到的3路源信号序列如图7所示。
通过FastICA 算法,将4 路信号分离后共得到3路独立的源信号序列,分别为源信号Z1序列、源信号Z2序列和源信号Z3序列。观察源序列波形图,可以看出前两路源信号与重构的呼吸信号有着良好的相关性,而源信号Z3 序列则保留了更多的基线漂移信号特征。由于本章主要需要获得人体呼吸率,故将对前两路源信号序列的结果着重进行对比分析。
3 EDR算法验证
由于人体呼吸率的频率低,频谱中存在较大其他频谱干扰,使得参数检测误差较大。因而采用时域的方法检测该参数更为有利。在时域内,采用下采样和滑动平均的方法对提取出的源信号序列进行滤波处理,得到更为准确的代表呼吸信号的序列[24],再采用峰值查找法标记出各序列的峰值。将基于FastICA算法得到的Z1序列和Z2序列峰值与基于R波幅度调制和基于S波幅度调制提取的呼吸波形峰值相比较,各信号序列的峰值标记波形图如图8所示。
由图8可以得知,应用FastICA算法得出的两路源信号Z1和Z2序列与基于R波或S波幅度调制方法提出的呼吸信号波形均有着良好的相关性,将该4路信号的幅值进行归一化,得到4路信号的波形如图9所示。
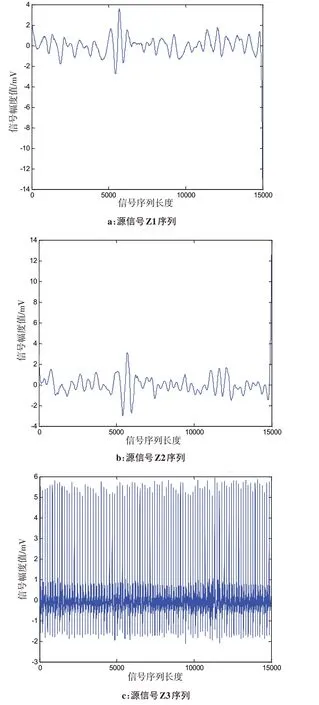
图7 ICA得到的3路源信号序列Fig.7 Three source signal sequences obtained with independent component analysis

图8 各信号序列的峰值标记波形图Fig.8 Waveforms with labeled peak signals of each signal sequences

图9 归一化幅值的4路信号波形序列Fig.9 Four signal waveform sequences with normalized amplitude
统计数学上,常用内积来反映各数据间的关联性。经计算得到4 路信号的内积值如表2所示。内积值越接近1,表明两数据的关联性越大。内积值越接近0,说明两列数据不相关。从内积表中,我们可以得出经过ICA 得到的Z1 序列和Z2 序列均可以提取出呼吸信号。因此,将Z1序列和Z2序列二者数据取平均得到新的代表呼吸信号的序列。
通过滑动平均法检测序列的峰值,各序列统计得到的峰值数值即反映了人体每分钟呼吸次数。将现有的24 h 连续信号以每2 h 为间隔,共分为12 段,对每段内的1 min时长信号序列进行峰值统计,共累积统计120 min 内的呼吸总数,最后,通过求平均得到的每两小时内呼吸率结果如表3所示。
4 结论
为了减少额外医疗设备的使用,降低受测者的不适感,本文提出一种EDR 算法。首先选用几路相互独立的涵有呼吸信号的数据序列,其次运用ICA分析方法分离出源信号序列,然后将得到的源信号序列与其他方法提取的呼吸信号序列进行比较,最后确定以ICA 分离出来的两路信号的均值作为提取的呼吸信号序列。从验证的结果来看,每分钟内呼吸率检测结果在人体正常情况下每分钟呼吸结果范围内,证明了上述各种算法的正确性,虽然在时域内峰值的检测存在一定的误差,但是通过该方法提取出的呼吸信号波形与其他方法提取出的呼吸信号存在良好的相关性,其平均相似度达到95.94%以上,说明该方法提取呼吸信号的有效性。并且,使用该算法避免了各种复杂滤波器的设计,算法实现简单,满足了一般病人呼吸参数检测的需求,具有相当的实用价值和意义。

表2 4路信号序列的夹角余弦值Tab.2 Cosine coefficient of 4 signal sequences
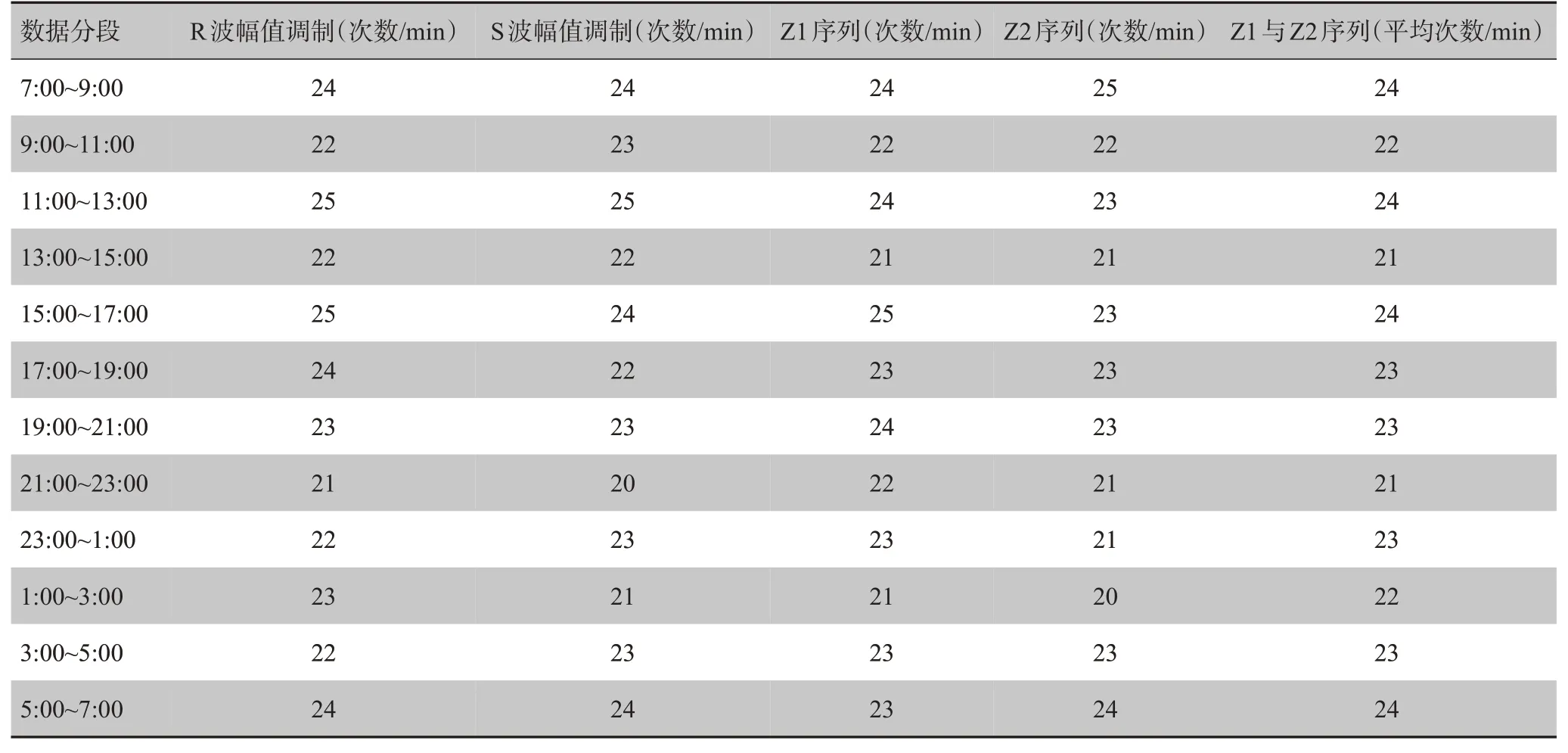
表3 EDR算法仿真结果比较Tab.3 Simulation results of EDR algorithm
