挑战中感悟知识 反思中提升能力
2019-04-27许燕
许 燕
在自然界和人类社会生活中,严格确定的现象十分有限,不确定的随机现象却大量存在。概率是对随机现象的一种描述,它可以为人们合理、理性地决策提供依据。学完了“认识概率”这一章,你对概率的认识有多少呢?本文整理了同学们在平时作业中常出现的几种典型错误,并对错误的原因进行分析。聪明的你不妨对照一下!
一、挑战中感悟知识
专题1 事件类型的确定
例1下列事件中,确定事件有( )个。
(1)“飞人”刘翔110米跨栏,只用了6秒钟;(2)天阴了,将会下雨;(3)一个数的平方一定不是负数;(4)字母a表示一个数,则-a表示负数;(5)两条线段可以组成一个三角形。
A.4个 B.3个 C.2个 D.1个
【错解】A或C或D。
【正解】B。
【学生自述】对确定事件理解不透彻。
【点评】(2)(4)是不确定事件;(1)(5)是确定事件中的不可能事件;(3)是确定事件中的必然事件。必然事件和不可能事件统称为确定事件。所以确定事件有3个。答案选B。
专题2 比较随机事件发生的可能性的大小
例2如果一个事件不发生的概率为99%,那么这个事件( )。
A.必然发生 B.不可能发生
C.发生的可能性很大 D.发生的可能性很小
【错解】A或B或C。
【正解】D。
【学生自述】如果一个事件不发生的概率为99%,则误认为该事件就不可能发生。
【点评】要知道随机事件发生的可能性有大有小。此随机事件不发生的概率为99%,只能说明其发生的可能性很小,但并不是不可能发生。所以答案选D。
例3世界杯决赛有8个小组,每个小组有4个队。小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,选出2个队进入16强,胜一场得3分,平一场得1分,负一场得0分。(1)求每个小组共比赛多少场?(2)在小组比赛中,现有一个队得到6分,该队出线是一个确定事件,还是不确定事件?
【错解】(1)12场;(2)是确定事件。
【正解】(1)6场 ;(2)是不确定事件。
【学生自述】(1)忽视了是单循环比赛;(2)考虑问题不全面。
【点评】(1)由于是单循环比赛,所以每一个小组的4个球队应该比赛4×3÷2=6(场)。(2)因为总共有6场比赛,一个球队每场比赛最多可得3分,则6场比赛最多可得3×6=18分。现有一个队得6分,还剩下12分,则可能有2个队同时得6分。故不能确保该队出线。因此该队出线是一个不确定事件。
专题3 体会概率的现实意义,解决实际问题
例4在2012—2013赛季NBA常规赛中,科比罚球的命中率大约是83.3%。下列说法错误的是( )。
A.科比罚球投篮2次,一定全部命中
B.科比罚球投篮2次,不一定全部命中
C.科比罚球投篮1次,命中的可能性较大
D.科比罚球投篮1次,不命中的可能性较小
【错解】B或C或D。
【正解】A。
【学生自述】不能正确理解概率的现实意义。
【点评】由科比罚球投篮的命中率来估计科比当前投篮的命中情况,虽然以往命中率为83.3%比较高,但不表示一定会命中。所以答案A是错误的。
专题4 概率与频率的关系
例5“六一”儿童节期间某玩具超市设立了一个如下图所示可以自由转动的转盘,开展有奖购买活动。顾客购买玩具就能获得一次转动转盘的机会。当转盘停止时,指针落在某一区域就可以获得相应奖品(铅笔或文具盒)。下表是该活动的一组统计数据。下列说法正确的有( )个。

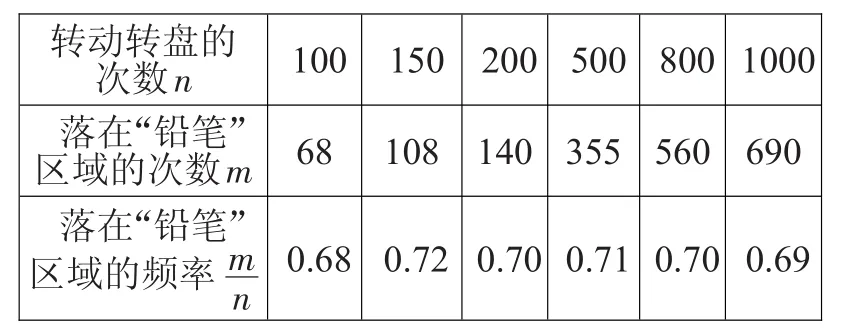
(1)当n很大时,估计指针落在“铅笔”区域的频率大约是0.70;(2)假如你去转动转盘一次,获得铅笔的概率大约是0.70;(3)如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;(4)转动转盘10次,一定有3次获得文具盒。
A.4个 B.3个 C.2个 D.1个
【错解】A或C或D。
【正解】B个。
【学生自述】选错的原因是对频率和概率的关系没有理解透彻。
【点评】在充分多次试验中,一些事件的频率总在一个定值附近摆动,试验次数越多,摆动幅度越小,这个性质称为频率的稳定性,所以(1)是正确的,此时可用频率的稳定值来估计事件的概率。转盘指针落在“铅笔”区域和“文具盒”区域的概率分别为0.70和0.30,因此(2)(3)是正确的。(4)转动转盘10次,一定有3次获得文具盒的说法是错误的。所以说法正确的有3个,答案选B。
二、反思中提升能力
1.下列成语,刻画的是必然事件的是____,刻画的是不可能事件的是________,刻画的是随机事件的是_______。(选填序号)
(1)万无一失;(2)胜败乃兵家常事;(3)水中捞月;(4)十拿九稳;(5)海枯石烂;(6)守株待兔;(7)百战百胜;(8)九死一生。
2.王强与李刚两位同学在学习“概率”时,做试验来抛一枚质地均匀的正方体骰子。他们共抛了54次,向上点数出现的次数如下表:
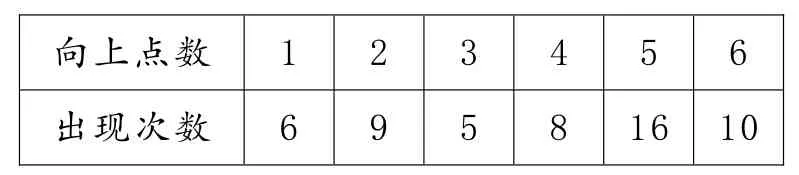
(1)请计算向上点数为“3”的频率及向上点数为“5”的频率;(2)王强说:“根据试验结果可知,一次试验中出现向上点数为5的概率最大。”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次。”请判断王强和李刚说法的对错。
【答案】1(.1)(7);(3)(5);(2)(4)(6)(8)。
