舰船主动力装置故障隔离与参数估计方法*

黄 林，程 刚，朱国情，陈于涛

(海军工程大学 舰艇装备仿真技术研究所， 湖北 武汉 430033)

舰船主动力装置是舰船至关重要的组成部分，包含了主机、传动装置、推进轴系和推进器等。由于结构复杂且工作环境恶劣，因此故障率较高，但舰船机舱空间狭窄，管路系统复杂，发生故障后很难通过肉眼观察进行排查[1]。基于上述特点，针对舰船主动力装置的故障诊断与隔离问题一直是重要的研究课题。

基于数学模型的故障诊断技术是近年来发展较快的一种方法。通过建立一个能够准确描述系统动态变化过程的数学模型，在其基础上，推导系统的解析冗余关系(Analytical Redundancy Relations, ARRs)，建立系统的故障特征矩阵(Fault Signature Matrix, FSM)，再通过在线对系统故障特征向量进行观测，可以实时地对系统进行故障诊断与隔离。基于解析模型故障诊断的准确性与实时性很大程度上取决于系统模型的质量。针对复杂系统建模与故障诊断问题，键合图理论以其规范化、系统化和支持多能域耦合建模的特点，为复杂系统的故障诊断提供了一个便捷、有效的方法。参数估计是在系统故障隔离基础之上，采用一定的数学算法对系统中的不确定性参数进行估计，掌握和分析系统的故障程度，这对于缓慢性故障的诊断具有非常重要的意义，可以应用于系统的健康状态评估，将事后维修随后逐渐发展到基于运行状态的状态维修，从而对主动力装置进行快速和准确的评估[2]。

在国外，Samantaray等[3]、Bouamama等[4]、Merzouki等[5]和Loureiro等[6]针对基于键合图理论的建模与故障诊断问题进行了大量深入的研究，其中最具代表性的为Samantaray等[7-8]针对锅炉蒸汽系统进行的键合图建模，以及基于该模型的故障诊断方法研究，充分证明了即使是对于蒸汽系统这样复杂、强非线性的系统，基于键合图理论的建模与故障诊断方法同样是适用的。在国内，樊久铭等[9]建立了液体火箭发动机的故障诊断键合图模型并进行了故障诊断的仿真验证。牛刚等[10]针对机车制动系统故障检测与隔离的问题，建立了系统键合图模型，提出了采用序贯概率比方法对系统残差进行跟踪判断，实现了部件的故障诊断与隔离。黄志武等[11]采用同样的方法，针对法维莱制动机系统，推导计算了系统解析冗余关系，得到了系统故障特征矩阵，并将该方法进行了实际应用。彭小辉等[12]针对航天器推进系统的时变特性，在系统键合图模型的基础上，采用了Z检验分析与解析冗余关系相结合的半定性故障隔离方法，实现了对部件的故障检测与隔离。

基于双因果键合图模型的故障诊断是在上述研究方法上的进一步创新，相比于文献[9-12]所采用的因果关系倒置诊断键合图模型(Diagnostic Bond Graph, DBG)，双因果键合图可以帮助建模者以更灵活的方式进行系统因果关系的指定。一方面，通过对因果路径的分析，在推导系统ARRs时不需要形成具体的数学表达式，减少了大量的工作。另一方面，相比于传统的键合图模型，双因果键合图模型中的故障部件同时接收了系统流变量和势变量的信息，因此，根据部件的构造方程，可以实现部件的参数估计，实时地跟踪故障状态参数，具有非常重要的现实意义。

文献[13]以两水箱系统为例，研究了基于双因果键合图模型的故障诊断与隔离问题，文献[14]提出了基于双因果键合图模型的参数估计方法，并以一小型的移动机器人为对象进行了方法的验证。

针对舰船主动力装置的故障隔离与参数估计的问题，提出采用基于双因果键合图模型的定量故障隔离与参数估计方法。

1 系统分析与建模

键合图理论最早由Paynter教授在20世纪60年代初提出，后经推广，逐渐成为一种系统动力学图示建模方法[15]。

1.1 舰船主动力装置键合图建模

图1所示为某型舰主动力装置的键合图模型，该型舰采用的主机为16PA6-280STC涡轮增压柴油机，文献[16]建立了该型柴油机的键合图模型并进行了详细的试验验证，柴油机模型即采用该模型。飞轮是保证柴油机连续运转的非常重要的部件，采用惯性元件Ifly对其进行建模。主机通过离合器与齿轮箱接合，在不考虑接合和脱开操作的情况下，离合器可以采用Ccul和Rcul进行表示(文献[17]建立了更为详细的离合器键合图模型)，分别为其扭转刚度和阻尼。变换器TF表示齿轮箱传动；Ipinion，Igear，Rpinion，Rgear和Cgear分别表示齿轮箱小齿轮转动惯量、大齿轮转动惯量、小齿轮摩擦阻力、大齿轮摩擦阻力和扭转刚度[18]；Ccoup和Rcoup分别表示万向联轴器的扭转刚度和阻尼；Ishaft和Rshaft分别表示轴系的转动惯量和摩擦阻力；Rcpp为螺旋桨，Ivessel表示船体的质量。推力轴承连接万向联轴器，固定在船体上，用于传递柴油机功率和承受螺旋桨推力，其简化成了以航速为输入变量的阻力模块Rthrust。模型中略去了部分对模型整体动态特性没有影响并且故障率非常低的部件，例如用于连接主机与齿轮箱的高弹联轴器、水润滑轴承等。

根据造船厂提供的“主推进装置控制监测系统测点表”，除去部分辅助系统以及温度或开关量测点，与本研究对象相关的传感器测点有(在图1所示的模型中进行了标明)：柴油机转速传感器Df ∶N，轴扭矩传感器De ∶τshaft，大齿轮和小齿轮转速传感器Df ∶Npinion和D ∶Ngear，轴转速传感器Df ∶Nshaft，桨扭矩传感器De ∶τcpp，航速Df ∶vs，油门齿杆位置传感器和柴油机功率传感器。

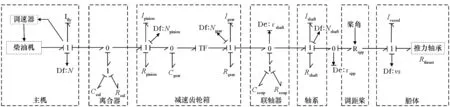
图1 舰船主动力装置键合图模型Fig.1 Bond graph model of the marine main power plant

1.2 BG-LFT故障建模

BG-LFT故障建模[19]是在系统键合图模型的基础上，提供一种简洁明了的基于故障机理的图示化故障建模方法，采用该方法可以非常方便地进行系统设备、执行器和传感器等的故障模拟。

假设阻性元件Rn上作用有一个乘性故障，如图2所示，则其发生故障后输出的故障势变量大小为：

eF=Rn(1+FR)fR

(1)

式中，Rn为阻性元件在正常状态下的阻性值，FR为该乘性故障的故障因子。

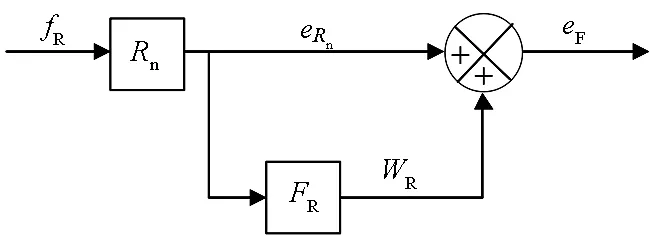
图2 阻性元件乘性故障方块Fig.2 Block diagram of an R-element with a multiplicative fault

图3所示为图2对应的BG-LFT模型。其中，故障因子Fn前的负号“-”，是由0节点和1节点的计算规则所确定；De*∶zFR表示该传感器为虚拟传感器，并不真实存在，其作用是解释模型的运算逻辑，使模型更容易被理解；可调势源MSe ∶WR表示由于故障WR的引入，而使得模型所产生的额外势变量的影响。

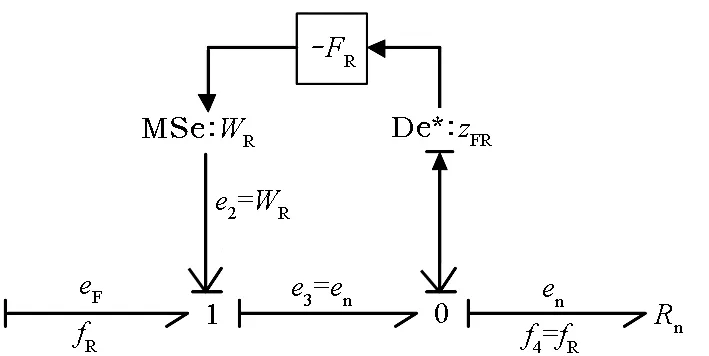
图3 阻抗型R元件乘性故障的键合图LFT模型Fig.3 BG model LFT of an R-element in resistive causality with a multiplicative fault

1.3 系统双因果键合图模型

双因果键合图的概念最早由Gawthrop教授提出[20]，用于研究基于键合图模型的系统逆向动力学以及系统参数及状态估计等问题。双因果键合图的功率键和其对应的因果关系如图4所示，并引入了几个新的元件，分别为源-传感器(Source-Sensor, SS)、势放大器(Amplifier of Effort， AE)、流放大器(Amplifier of Flow， AF)。双因果关系键的因果关系指定规则与传统键合图模型的因果关系指定规则的对比如图4(a)和图4(b)所示。

(a) 传统键合图因果关系 (a) Causality of traditional bond graph

(b) 双键合图因果关系 (b) Causality of bicausal bond graph
图4 双因果键因果关系规则
Fig.4 Information exchange in bicausal bonds

图4(b)为双因果键因果关系的两种表示方法，功率键的两端各有半截因果划，半箭头表明了系统内能量流动的方向。在双因果键中，由于势变量和流变量的指定方向一致，因此，根据键合图理论中0节点和1节点的特性方程和计算法则，对于连接有双因果键的节点来说，双因果键必须是成对出现，而且只能有两条，普通功率键的数量则没有限制。

图5所示为舰船动力装置的双因果键合图模型，该模型等同于文献[9-12]的诊断键合图模型，SSf和SSe作为信号源接收传感器的信号输入系统并进行系统残差的分析和诊断。ARR3至ARR9在其对应的结点元件处已标明。文献[13]证明了不管选择哪一个元件作为因果关系的结点，尽管其生成的FSM不同，但其部件的故障诊断特性都是相同的。

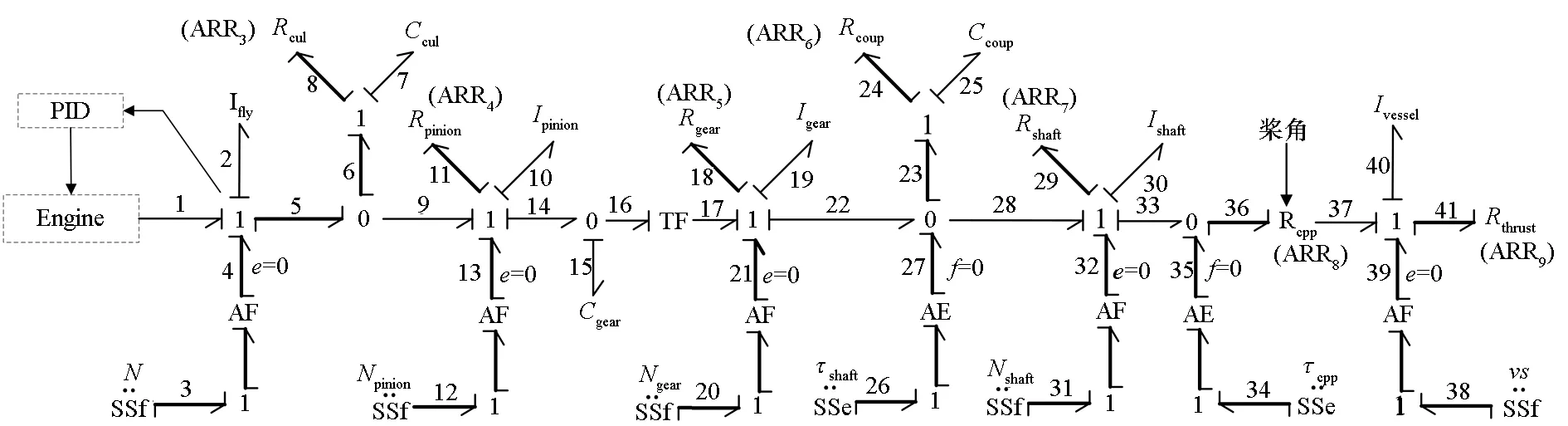
图5 舰船动力装置双因果键合图模型Fig.5 Bicausal bond graph model of the marine main power plant

2 舰船主动力装置解析冗余关系分析

2.1 舰船主动力装置ARRs

对于舰船主动力装置，ARR1和ARR2可以直接从调速器的控制输出油门齿杆位置和柴油机功率输出获得，例如，假设实际装备中的调速器发生故障，其输出的油门齿杆位置与模型控制器的输出将不一致，则通过ARR1可以立即进行调速器故障的判断。

由于双因果键合图对于每一个ARR都定义了明确的结点元件，因此可以直接通过因果关系的推导得到ARR路径上所有的部件，而不需要推导具体的ARR数学表达式，节省了非常大的工作量。例如，根据图5所示的舰船主动力装置的双因果键合图模型，传感器SSf ∶N对应的结点元件为Rcul，其对应的因果路径关系为：

由上述因果路径可得，ARR3(Rcul为对应的结点元件)包含的系统部件为：

ARR3=ARR3(Ccul,Rcul, Engine, Ifly)

(2)

ARR包含的部件越少，其所能进行故障诊断的针对性就越强。同理，根据模型因果关系，ARR4至ARR9的表达式分别为：

ARR4=ARR4(Engine, Ifly,Rpinion,Ipinion, TF,Cgear)

(3)

ARR5=ARR5(TF,Rgear,Igear,Cgear)

(4)

ARR6=ARR6(Ccoup,Rcoup)

(5)

ARR7=ARR7(Rshaft,Ishaft)

(6)

ARR8=ARR8(Rcpp)

(7)

ARR9=ARR9(Rcpp,Ivessel,Rthrust)

(8)

2.2 系统FSM

根据上述系统ARRs的表达式，实际装备中的9个传感器分别对应9个ARRs。因为，例如Ishaft和Rshaft都为轴系相关部件，并且系统部件的转动惯量一般不会发生变化，则其在FSM中可统一表示为轴系。Ifly也不需要在FSM中考虑，TF表示齿轮箱传动，因此，可以得到系统的FSM如表1所示。FSM最右侧两列Mb和Ib分别表示故障可诊断性和可隔离性。从表1中可以看出，在现有的传感器布置方案下，系统中所有部件的故障都是可诊断并且可隔离的。

2.3 基于双因果键合图的参数估计方法

参数估计指的是对发生故障部件的故障参数进行估计和预测。通过一定的算法，结合LFT模型以及双因果键合图，可以实现系统故障的参数估计。根据故障类型的不同，参数估计方法可分为设备故障、执行器故障和传感器故障，分别对应键合图模型中的储能和耗能元件(C，R，I)、源元件(Se，Sf，MSe，MSf)和传感器(De，Df)，虽然故障种类不同，但实现方法和原理是一致的，本文以设备参数故障为例，进行基于双因果键合图的参数估计方法研究。

假设舰船主动力装置经长时间服役后，轴系磨损加重，则装置中Rshaft对应的摩擦阻力将增大，其BG-LFT模型如图6(a)所示，其中FR为故障因子。图6(b)所示为对应的以Rshaft为结点元件的双因果键合图模型。

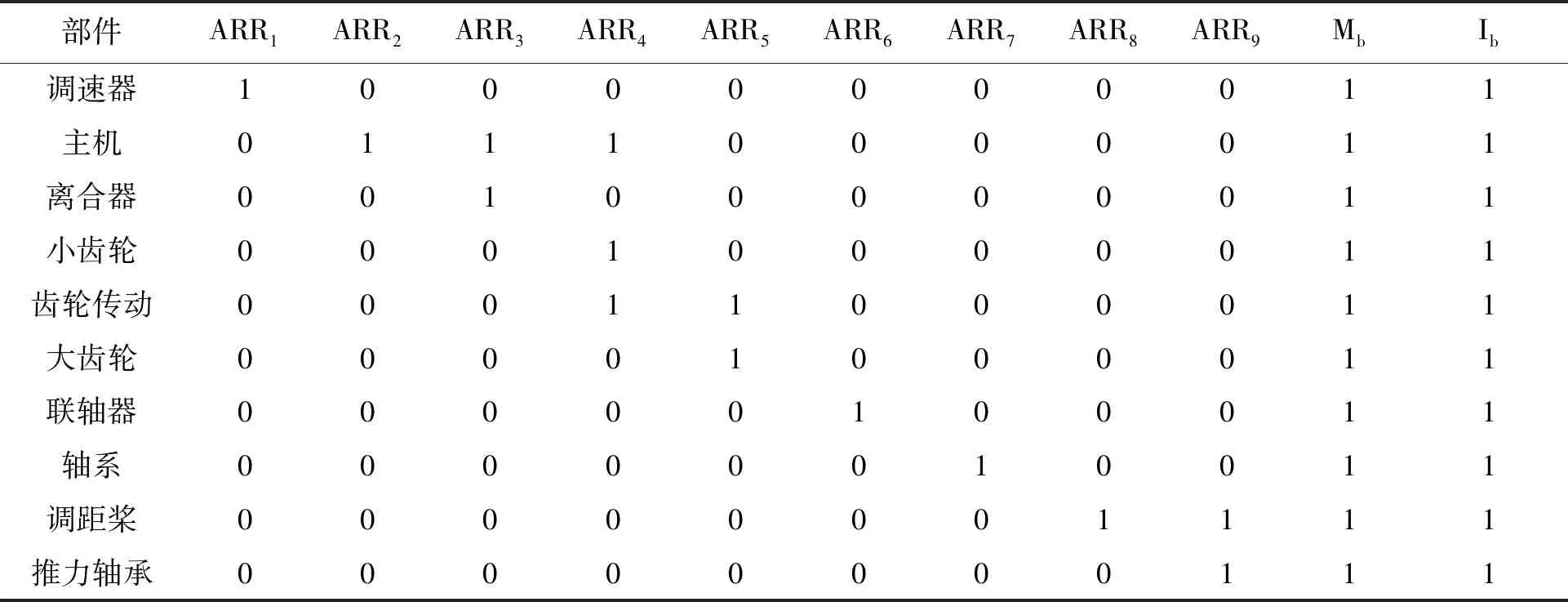
表1 舰船主动力装置故障特征矩阵

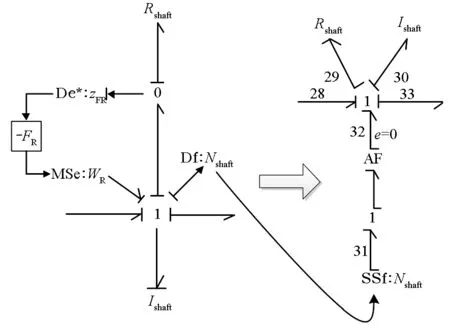
图6 阻性元件R的参数估计模型Fig.6 Fault estimation model of the R-element

在图6(b)中，假设系统正常运行，则根据1节点的系统解析冗余关系有：

(9)

BG-LFT模型故障注入后，Rshaft元件发生故障，轴系磨损量增大，系统解析冗余关系为：

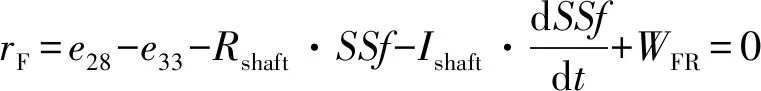
(10)

假设阻性元件Rshaft的故障是可隔离的，则可以通过双因果键合图的计算法则以及系统残差与故障系统之间的关系对系统发生的故障大小进行估计。根据双因果键合图因果关系计算法则，由BG-LFT模型中的势源和传感器的因果关系推导，可以得到发生在阻性元件Rshaft的故障值为：

(11)

zFR=R·SSf

(12)

(13)

3 仿真验证

3.1 系统模型与双因果诊断键合图模型的耦合

图7所示为舰船动力装置系统模型与双因果诊断键合图模型的耦合模型。为了验证本文理论方法的正确性，将系统的键合图模型与诊断键合图模型连接，用系统的键合图模型模拟实际系统，在系统中注入相应故障，通过诊断键合图模型进行检测。为了模拟真实环境噪声工况下传感器测量的不确定性，所有由传感器采集的系统模型信号都加入了相应的噪声污染，噪声信号采用MATLAB/Simulink中白噪音，噪声的振幅为传感器输出的0.1%，平均值为0。图7中W1至W9为噪声信号与传感器信号的叠加输出。仿真试验中，由于DBG模型多采用微分计算，为消除传感器输出信号在噪声干扰下由于微分计算而产生的异常阶跃，采用算术平均滤波法，对传感器输出信号和残差信号进行了五点平滑降噪处理。在实际故障诊断的应用中，只需要将实际系统代替图7中的系统行为模型即可。模型中，r1至r9分别对应系统的9个残差。建立好模型后，建模者可以任意地对动力装置中的任何部件进行故障仿真试验，从而可以得到大量的离线故障仿真数据，这对于动力装置的后续健康状态检测具有非常大的帮助。

3.2 MATLAB仿真试验与结果分析

以比较典型的舰船长时间服役后，舰船主动力装置柴油机效率下降和轴系磨损加重为例，开展故障仿真，并进行故障诊断与隔离。

3.2.1 柴油机效率下降故障

仿真时间设置为1000 s，在第500 s的时候注入柴油机效率下降故障，使柴油机输出功率从100%降低至95%，图8所示为双因果键合图DBG模型ARR1至ARR9的动态响应。从ARR的响应中可以很明显地看出，ARR2，ARR3和ARR4对该故障是敏感的，其值非常明显地偏离了0的位置，其余残差均在0左右波动。ARR9在第500 s的时候有一点小波动，产生该现象的原因是柴油机输出功率的下降导致螺旋桨推力下降，而因为船体满载质量比较大，惯性也大，因此航速下降得比较慢，待系统重新稳定后，ARR9恢复至0。通过以上分析可以得到故障特征向量[0 1 1 1 0 0 0 0 0]，通过与表1的FSM进行对比，其柴油机所对应的故障特征向量是相匹配的并且是唯一的，因此可以知道是主动力装置中的柴油机发生了故障，该故障是可隔离的。

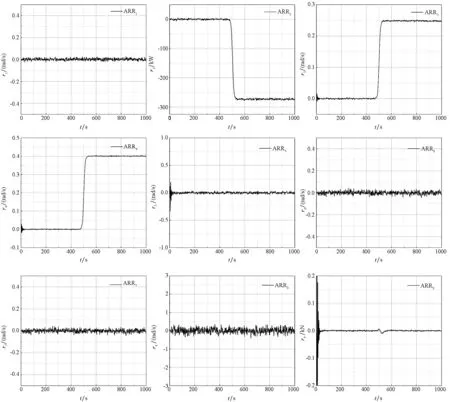
图8 柴油机效率下降故障残差响应Fig.8 Residuals response when engine efficiency decline

3.2.2 轴系磨损增加

设置轴系磨损故障因子为0.172，使磨损值正常的1450 Nms/rad增加至1700 Nms/rad，图9所示为在故障下系统双因果键合图DBG模型ARRs的动态响应。从ARRs的响应中可以很明显地看出，只有ARR7对该故障是敏感的，其值非常明显地偏离了0的位置，其余残差均在0左右波动。通过以上分析可以得到故障特征向量[0 0 0 0 0 0 1 0 0]，从而检测出系统中的轴系发生了故障，实现了该故障的诊断与隔离，验证了本方法的正确性。

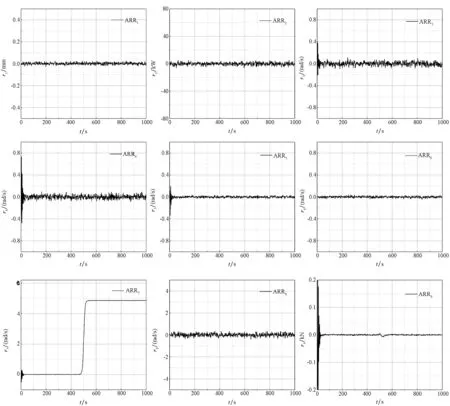
图9 轴系磨损增加故障残差响应Fig.9 Residuals response of the wear of shaft

3.2.3 参数估计仿真分析结果

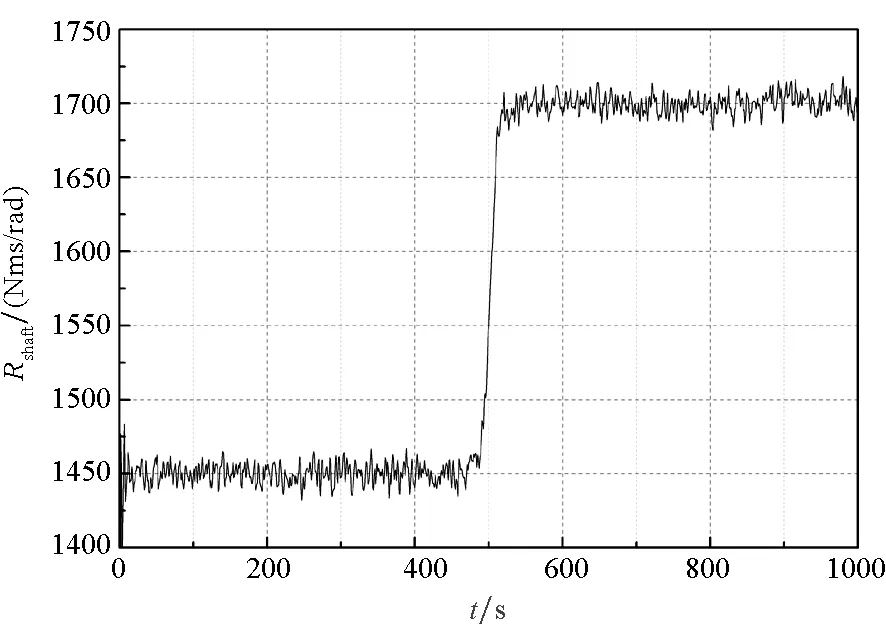
图10 轴系磨损故障参数估计Fig.10 Estimation of the friction of shaft

图10和图11所示为柴油机效率以及轴系磨损故障参数的估计值随时间变化的动态曲线，从图中可以看出，通过采用本文的方法，不管是故障前还是故障后，系统都能够很快地对故障参数进行实时估计。在故障注入后，系统能够非常迅速地对故障参数进行估计，并且是非常准确的。

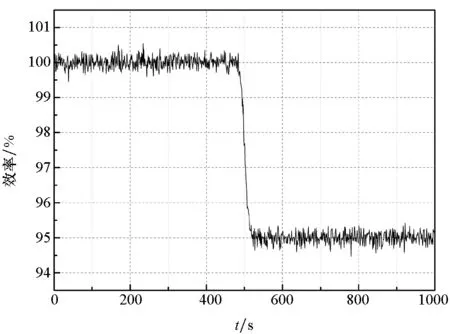
图11 柴油机效率下降参数估计Fig.11 Estimation of the efficiency of diesel engine

4 结论

提出了基于双因果键合图模型的定量故障隔离以及参数估计方法，利用该方法对舰船主动力装置进行了故障隔离以及参数估计仿真试验，结果表明：

1)双因果键合图模型具有更加明确和灵活的因果路径关系，通过对其进行分析推导可以直接得到系统ARRs，不需要复杂的数学推导过程。

2)在现有的传感器布置方案下，通过双因果键合图模型得到的系统FSM具有很好的故障诊断特性，舰船主动力装置中所有系统部件的故障都是可诊断和可隔离的。

3)键合图LFT模型可以很好地进行系统故障建模，将其与双因果键合图模型结合，可以方便地实现系统各种离线故障仿真，得到大量的系统故障数据。

4)基于双因果键合图模型的参数估计算法能够实现系统故障参数的估计并具有很好的实时性，在系统发生故障后，故障参数能够得到及时的反馈。