基于SIFT子图像融合的直角坐标FBP算法*
2019-04-26张佳琪李凉海张振华左绍山
张佳琪,李凉海,张振华,左绍山
(北京遥测技术研究所 北京 100076)
引 言
合成孔径雷达SAR(Synthetic Aperture Radar)具有全天时、全天候、高分辨率、大覆盖面积、成像不受天气和光照强度等影响的优点,广泛应用于军事侦察、地球遥感、资源勘探、农作物估产、自然灾害监测、环境保护等诸多国防和国民经济的重要领域。针对SAR不同的成像模式,国内外学者先后研究了各种不同的距离多普勒算法、时域成像算法和二维频域成像算法[1,2]。
后向投影算法BPA(Back Projection Algorithm)是SAR时域成像算法的典型,适用于任意场景、任意雷达工作模式成像,并且具有很好的并行性,易于工程实现。传统的BPA是基于极坐标系的,能直接从回波数据搜索出目标点的后向散射系数,对含有运动误差的SAR成像数据进行精确聚焦[3,4],但是其需要逐点遍历,计算量过大,效率低,不适用于SAR实时成像处理。后来有学者提出的快速后向投影算法FBPA(Fast Back Projection Algorithm)采用极坐标系,通过对子孔径进行相干积累来提高运算效率,但是由于不同极坐标系之间的关系是非线性的,因此需要通过逐像素投影来实现子图像融合,这就增加了计算量,并且在融合过程中为了提高融合效率,通常会采用一定的近似处理,导致成像分辨率、峰值旁瓣比等成像指标下降。左绍山等人提出一种改进的直角坐标系下的FBP算法[5],只需坐标平移即可实现直角坐标系下的子图像融合,既减少了计算量,又避免了极坐标下对融合的近似,提高了融合精度。同时该算法采用方位谱压缩技术解决了文献[6]所提到的局部直角坐标系下子图像的方位谱宽度要比局部极坐标系下子图像的方位谱宽度大从而造成子孔径信号后向投影成像过程计算量大的问题。但是随着分辨率的提高,天线相位中心与成像目标之间的运动补偿精度也越来越高,因此即使是装有先进惯性导航测量单元的SAR系统,要想精确补偿载机的运动也是很困难的,另外由于大气传播效应产生的相位误差也会使SAR高分辨图像散焦。而文献[5]算法没有对运动误差进行补偿,因此不适用于实测数据。针对实测数据,张磊等人提出了一种多孔径图像偏移自聚焦算法与时域快速后向投影算法相结合的算法,该算法仍是基于极坐标系的。选择方位角正弦为子孔径坐标系的方位坐标,后向投影成像的极坐标方位轴对应多普勒频率轴,对各子孔径极坐标成像直接进行逆傅里叶变换到方位时间域,在时间域实现各个子孔径数据的调频率估计,继而进行相位误差估计,实现快速后向投影成像过程中的自聚焦处理。
本文提出一种将直角坐标系下的子孔径FBP算法与基于尺度不变特性变换SIFT(Scale Invariant Feature Transform)的SAR图像配准方法相结合的算法,在减小计算量的同时,提高融合精度和算法的并行性,另外通过合理划分子孔径,达到实时处理的效果。本文将原始数据划分子孔径后,经过后向投影得到子孔径图像是基于直角坐标系的,在融合过程中无需将极坐标与直角坐标进行转换,亦无需先插值再融合,减小了计算量。然后通过特征点匹配完成子图像融合,达到提高成像效率与分辨率的目的。相比于文献[5],本文提出的方法进行了自聚焦处理,能够处理实测数据;相比于文献[7],本文提出的方法采用了一种新的融合方式,能够提高分辨率与融合效率。本文算法具有良好的并行性,为后续子图像融合而采用直角坐标FBP结合SAR实时成像算法的FPGA实现做准备。
1 基于SIFT子图像融合直角坐标FBP算法
直角坐标系下的FBP算法,是将整个合成孔径划分为若干个子孔径,在局部直角坐标系下以子孔径中心为原点重建子孔径图像,每幅子图像具有方位向低分辨和距离向全分辨的特点,在直角坐标系下将全部子图像进行一次方位平移,得到全孔径分辨率的SAR图像[8]。本文采用的融合方法与传统方法不同,本文基于SIFT特征点匹配的,即将子孔径图像进行特征点匹配,根据SIFT提取出来的特征因子找到不同子孔径图像之间的转换关系,利用转换关系完成子图像的融合,得到全孔径图像。本文算法的具体流程如图1所示。

图1 基于SIFT子图像融合的直角坐标FBP算法流程Fig.1 Based on SIFT sub image fusion for rectangular coordinates FBPA flow chart
算法主要包括以下四个步骤:
①将原始数据进行距离向脉压,并对脉压后的数据划分子孔径;
②对每个子孔径的距离脉压结果进行后向投影,得到各个子孔径回波的子图像;
③对子图像进行相位梯度自聚焦处理;
④对处理后的子图像进行SIFT特征点提取,将相邻子图像的特征描述符作匹配,完成子图像匹配融合,得到全孔径图像。
本文算法是基于直角坐标系的,在完成子图像SIFT特征点提取、特征点匹配之后,亦无需插值,无需逐点操作,只需按照坐标转换关系进行方位向的平移即可完成子图像融合。本文算法在子图像融合过程中采用上采样后的复图像作融合,相比于传统的基于实图像的融合,分辨率能够提高一倍。下面对算法的具体实现过程进行介绍。
1.1 直角坐标系的FBP算法
对已知场景中任意点目标N(x,y)的回波基频信号作距离向脉冲压缩,可以得到脉压的结果为

其中,c为电磁波传播速度,B为信号带宽,aa(tm)为雷达方位窗函数,tm为方位慢时间,为距离快时间,λ为雷达发射信号波长,R(tm;x,y)为任意tm时刻点目标(x,y)到雷达的距离。
接下来完成子孔径划分,再将每个子孔径信号经过后向投影算法得到对应的子图像,第i个子孔径对应子图像的表达式为
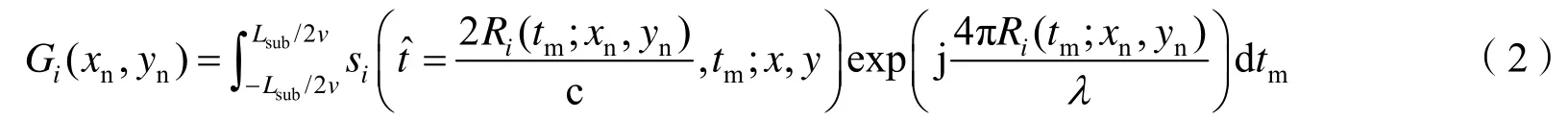
式中,v为雷达平台飞行速度,(xn,yn)表示子图像中网格点的坐标。将瞬时斜距在vtm=xn处进行泰勒级数展开,并将展开结果代入式(2)可以得到

式(3)最后一个指数项会导致方位向频谱展宽[9]。对于第i个子孔径,取近似refnR≈y,Rref为参考距离,可以得到降低方位谱宽度函数为

为了降低方位谱宽度,可将式(3)与式(4)相乘。如此一来,方位谱宽度变窄,成像网格方位间距变大为λyn/Lsub。因此在子孔径后向投影成像过程中,将像素方位间隔设置为小于成像网格方位间距,使得方位采样点数减少,进而降低了计算量,提高了子孔径成像效率。
1.2 自聚焦处理
自聚焦的目的是将相位误差补偿到合理的限度,便于对实测数据进行聚集成像处理。目前常用的自聚焦算法包含子孔径相关算法MD(Map Drift),相位差算法PD(Phase Difference),相位梯度自聚焦算法PGA(Phase Gradient Autofocus)等。PGA算法是目前研究的最成熟的算法且较MD算法来说更适用于估计高阶相位误差,并且由于本文子图像仅仅是经过了距离向脉冲压缩而没有对方位向进行处理,所以可以对子图像采用相位梯度自聚焦算法作相位补偿,以满足SAR成像高分辨率的要求。PGA方法基于最大似然估计理论进行最优估计,并且利用了多个距离单元上的相位误差信息,能够提高估计结果的稳健性[10]。
PGA算法流程如图2所示,从复图像域出发,以迭代的方式,逐渐改进图像的聚集,主要包含以下四个步骤:
①循环移位:首先需要在每个距离单元上选取最强散射点,并将其循环移位到孔径中心对应的位置。循环移位能够保留相位误差对所选取散射点的影响,还能去除与目标相关的线性相位分量。对于包含较少孤立散射点的一幅散焦的图像来说,循环移位是把各距离单元上的强点进行排列,从而有利于确定窗宽,而正确的窗宽选择能够改善相位估计信号的信噪比。
②加窗:对经过循环移位后的数据加矩形窗,能够保持最强散射点所包含的模糊信息,同时能够减少来自背景杂波或其它邻近目标的影响,使得用来估计相位误差的数据具有较高的信噪比。
③相位误差估计:由于相位误差估计是在距离压缩方位历史域进行,因此经循环移位和加窗处理后的图像数据首先要进行方位向傅里叶反变换。Jakowatz等利用特征矢量的方法,进行相位误差的最大似然估计,并且证明了估计方差达到克拉美-罗限[11]。对于第n个距离单元,当只采用相邻的两个方位向数据进行估计时,相位差为
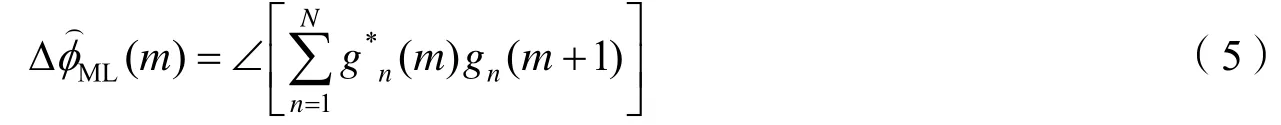
其中g*n(m)为距离压缩相位时域数据,m=1,2,3,…,M,M为方位向脉冲数,n=1,2,3,…,N,N为距离向脉冲数。通过累加可算出全部孔径上的相位误差,即

④迭代相位校正:将距离压缩方位历史域的数据与相位误差估计进行共轭相乘,经过傅立叶变换到图像域,即可改善图像聚焦。这一估计和校正过程需要重复迭代四至六次,以逐渐提高图像的质量[12]。
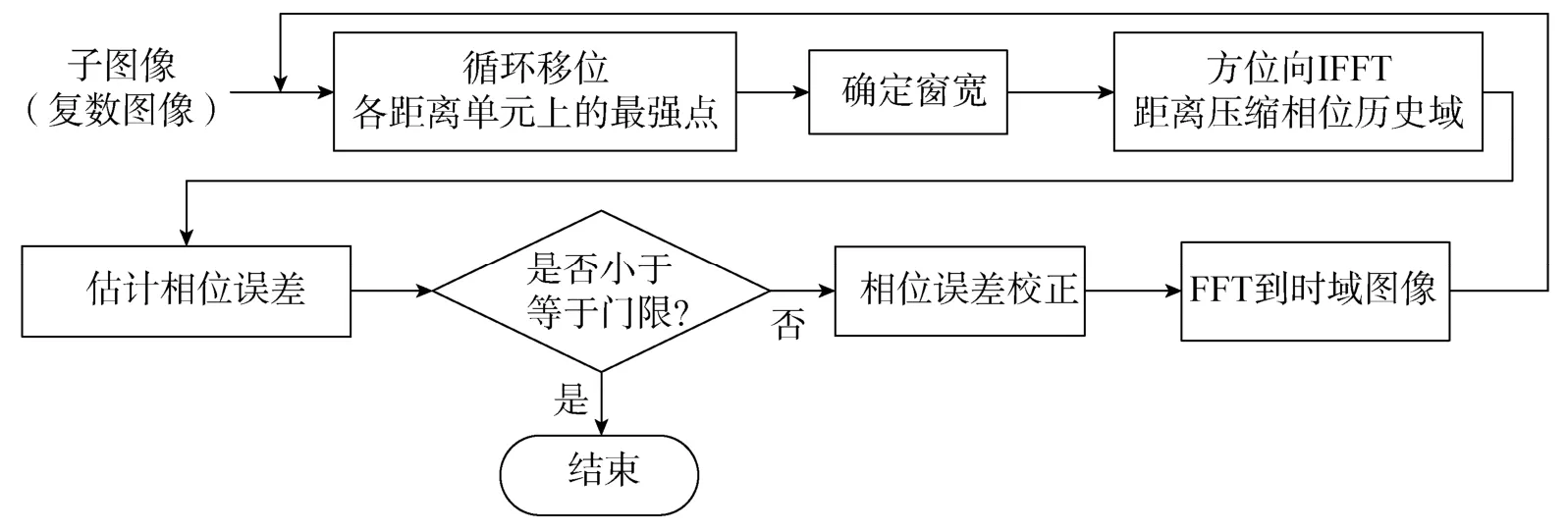
图2 PGA流程Fig.2 The PGA work flow
1.3 基于SIFT的子孔径融合
下面以两个子图像融合为例来说明基于SIFT图像匹配算法进行图像融合的基本流程。本文采用的SIFT方法与传统方法不同,它首先利用实图像获得特征点与融合移动量,然后用复图像进行融合,其流程如图3所示,可以概括为如下三个过程[13]:

图3 SIFT匹配算法Fig.3 SIFT matching algorithm framework
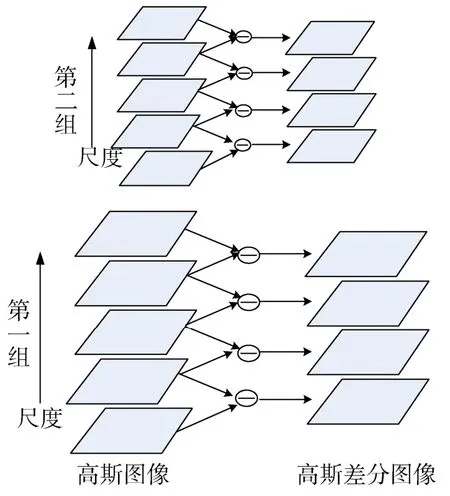
图4 构造DOG尺度空间Fig.4 Construction of DOG scale space
①提取实数子图像中的尺度不变特征点;
②对两幅图像检测到的特征点进行描述,以形成特征描述符;
③将实图像1与实图像2的SIFT特征描述符进行匹配,对复数子图像1和2按照匹配好的特征点进行平移,完成子图像的复值融合。
与传统的快速后向投影算法的融合方式相比,本文基于SIFT的融合采用的是子图像在时域的复数结果直接进行累加,能够提高分辨率,具体实现过程如下:
①图像极值点提取
首先利用高斯函数G(x,y,σ)获取子图像GH1(x,y)的尺度空间L(x,y,σ),其中σ为方差。具体过程为
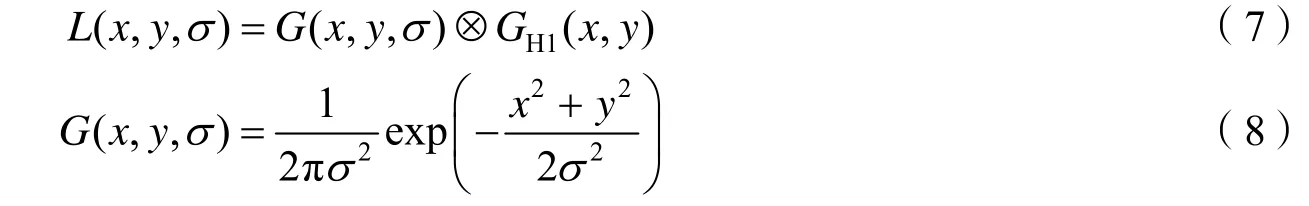
式(8)是均值为0、方差为σ的标准二维高斯函数。高斯卷积可以得到相邻尺度空间的图像,然后对其进行差分,得到高斯差分尺度空间DOG(Difference of Gaussian scale-space),过程如图4所示。尺度空间极值检测过程如图5所示,在高斯差分尺度空间中选定一个图像中的一个采样点与其上下各一幅相邻图像中的8个邻域点进行比较,判断其是否为极值点,如是则设置为粗选极值点。
②精确定位极值点
在获得了所有的粗选极值点之后,还需要进一步筛选,删掉那些对比度较低的点,以提高算法匹配的稳定性、增强最终极值点的抗噪性,具体通过拟合三维二次函数来实现。
将尺度空间函数D(x,y,σ)在待定点X处,进行泰勒级数展开,得到
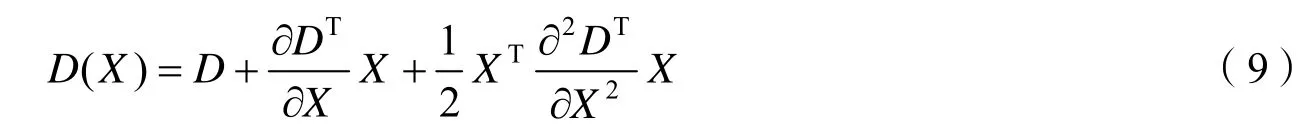
其中X=(x,y,σ)T。通过式(9)对X求导结果取0,可以得到极值点的偏移量为

若式(10)的极值点偏移量x与y中有一个数值超过0.5,可以判断极值点偏向另一端的待选点。此时,再以该点为待选点重复上述过程,直到有较精确的点,即获得最后的,该较精确的点与插值中心点的距离在任意一个方向上的偏差小于其到相邻点的距离。如此得到的特征点的精度可达到亚像素级。
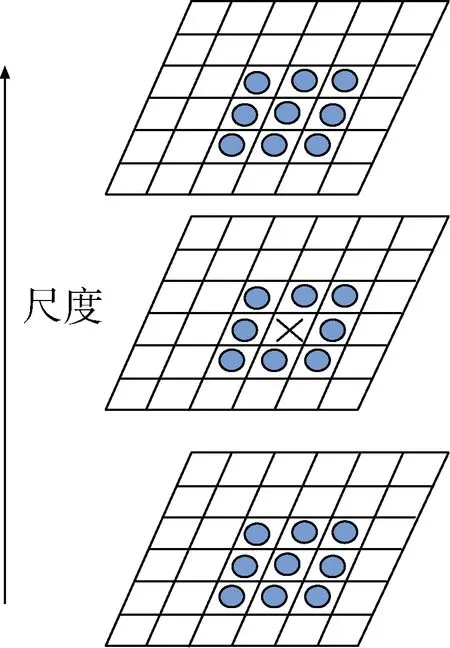
图5 尺度空间极值检测过程Fig.5 Scale space extreme detection

图6 SIFT算法融合过程Fig.6 SIFT algorithm mix process
③生成特征描述符
在通过前面的处理获得图像特征算子的位置信息之后,能够得到尺度不变特征算子。此外,由于每个特征点的邻域像素内梯度方向分布的不同,通过计算每个特征点的方向参数,使得特征算子具备旋转不变性的特点。
根据特征点位置选择离它最近的高斯平滑图像L,对其中的每个采样点L(x,y),在其四邻域内利用下式计算获取该点的梯度幅值m(x,y)和方向角θ(x,y)。
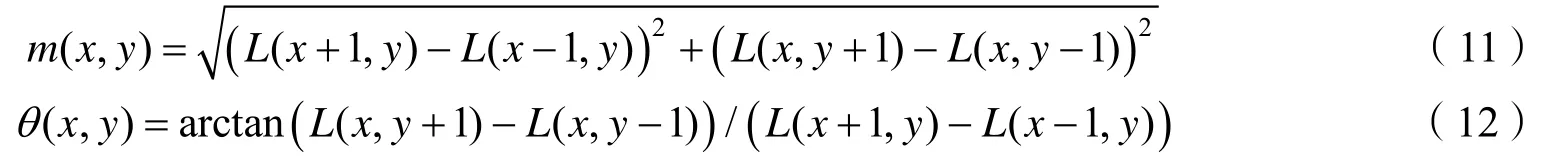
在实际中,为了提高图像匹配的稳健性,可以对每个特征点采用4×4个种子点进行描述,得到128维SIFT特征描述符。
④ SIFT 特征匹配与图像融合
在获取图像的特征描述符之后,还要对待匹配的两幅图像间的SIFT特征描述符进行相似性度量,本文采用经典的SIFT方法,即采用欧式距离进行度量。

特征匹配完成后,需要对提取出的匹配特征点对进行最小二乘算法拟合,得到最优相似参数包括:平移量、尺度的伸缩变化量、旋转角度,然后得到变化矩阵。以相邻两幅子图像中特征匹配度高的区域为基准,完成子图像的融合拼接,直至融合完所有的子图像,得到一副拼接好的全孔径图像。由于本文采用直角坐标系的FBP算法,能够根据匹配特征点对直接进行融合而无需坐标转换或插值,提高了融合效率。图6举例说明了采用SIFT算法的融合过程。
2 数据处理结果
为了验证本文所提出方法的有效性,本文首先采用条带模式下点目标仿真的方式,验证改进后的FBP算法的有效性,然后结合机载实测数据验证基于SIFT子图像融合的直角坐标系下的FBP算法在实测数据成像中的有效性。以下是实验结果。
2.1 点目标仿真结果
以条带模式为例,点目标验证结果如下。本文仿真了一个3×5的点阵目标,仿真参数如表1所示,最终的成像结果如图7所示,可以看到各点目标均能得到良好聚集。

表1 条带模式下的点目标仿真参数Table 1 Stripmap SAR point target simulation parameters
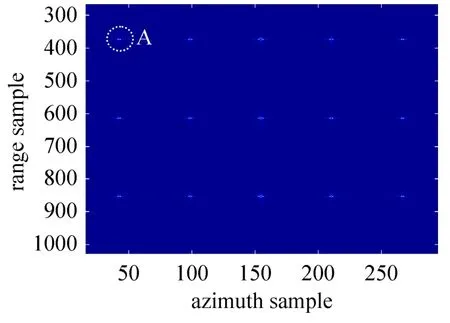
图7 点目标仿真结果Fig.7 Focusing results with simulated data
为了定量分析,本文将左上角点目标A的特性进行具体分析如图8所示,计算得到点A距离向和方位向的峰值旁瓣比分别为-13.44dB和-13.19dB。参考文献[14]的评估方法,方位向的峰值旁瓣比能达到-13dB以上,因此本算法的成像结果在方位向具有良好的聚集效果。

图8 点目标A的距离和方位包络Fig.8 Point spread functions of target point A
2.2 实测数据处理结果
实测数据采用的是某无人机SAR录取的回波数据,原始回波数据大小为900×8192(距离×方位),划分为8个子孔径,每个子孔径包含1024个脉冲,将原始回波数据进行惯导补偿与运动补偿后采用本文的成像算法得到拼接前子孔径图像。本小节以第3个、第4个子孔径融合为例说明采用SIFT方法的融合过程与效果。
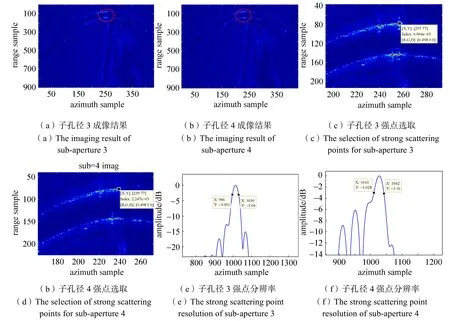
图9 子孔径3、子孔径4成像结果Fig.9 The results of sub-aperture 3 and sub-aperture 4
第3个、第4个子图像的结果分别如图9(a)、图9(b)所示。对其中包含强点的区域放大可以得到图9(c)、图9(d)的结果,根据SIFT得到的坐标关系,选取的强点如图9(c)、图9(d)所示,两幅图像的两个强点具有相同的距离向坐标和不同的方位向坐标。分析这两个强点的3dB方位分辨率特性如图9(e)、图9(f)所示,融合前第三个子图像分辨率为2.2203m,融合前第四个子图像分辨率为1.7128m。
完成SIFT子图像拼接的结果如图10所示。图10(a)、图10(b)分别表示SIFT融合前第3个、第4个子孔径图像,图10(c)、图10(d)分别为子图像3、子图像4的特征描述符,图10(e)为子图像3、子图像4的SIFT匹配特征点对,图10(f)为子图像3、子图像4融合后的图像。

图10 子图像拼接过程Fig.10 The process of the sub-aperture mosaic
仍然选取图9(c)位置的强点并分析其3dB的方位向分辨率,结果如图11所示,该强点处分辨率为1.1419m,与图9(e)、图9(f)相比,分辨率均有提高。
表2为采用SIFT方法找到的每一幅子图像的特征点。将全部子孔径进行拼接,可以得到拼接后的全孔径图像如图10(g)所示。从图10(g)可以看出,拼接结果良好,图像无错位现象产生也没有拼缝产生,而且采用SIFT融合比传统的融合办法得到的图像分辨率高,实测数据处理结果验证了本文算法的有效性。
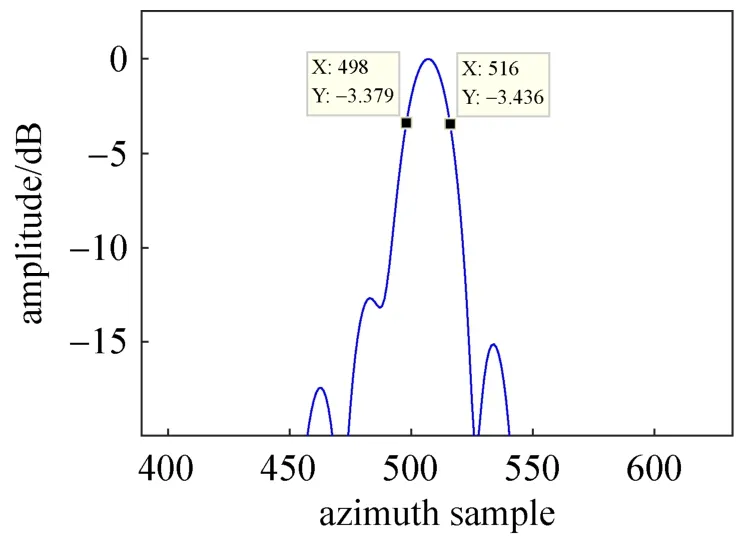
图11 子图像拼接后的强点的分辨率Fig.11 The resolution of strong character point after sub-image fusion
3 结束语
针对SAR实测数据计算量大的问题,本文提出了一种基于SIFT子图像融合的SAR子孔径成像算法,将基于尺度不变特性的融合方法与直角坐标系下的快速后向投影算法相结合,解决了传统后向投影算法计算量大的问题,另外进行子孔径划分可以提高算法的并行性,为后期FPGA的实时SAR成像处理提供方便。本文采用的SIFT融合方法是对复数图像的融合,能够提高全孔径图像的分辨率。数据处理结果表明,该方法能够提高SAR成像分辨率,并且很好地解决了BP算法计算量大的问题。后期研究将围绕SAR子孔径成像算法及其FPGA实现问题展开。

表2 各子图像特征点数目Table 2 Number of every sub image features points
