送风井位于隧道中部的半横向分区段通风特性研究

王明年，张建斌，邓涛，于丽，王旭



送风井位于隧道中部的半横向分区段通风特性研究

王明年1，张建斌2，邓涛1，于丽1，王旭1

(1. 西南交通大学 土木工程学院，四川 成都 610031；2. 厦门路桥工程投资发展有限公司，福建 厦门 361009)

为了确定一种送风井位于隧道中部，隧道内需风量存在分区段变化的半横向通风方式计算方法，以厦门海沧疏港通道-芦澳路城市地下互通隧道工程为依托，采用理论分析和数值模拟研究方法对风道内的压力分布进行研究，并对比送风井位置对风机压力的影响。研究通过在风道末端与风道内任意断面建立一元伯努利方程推导风道末端风速为0和风速不为0 2种情况下风道内的压力分布求解公式，数值计算结果验证了公式的正确性。根据研究结果，送风井位于隧道中部时，两侧风道始端全压可以视为相等，送风机提供满足通风压力较大一侧所需全压即可实现整个隧道的有效通风，该通风方式在增大通风长度适应性以及减小风机功率，以及提高经济性方面具有显著的优势。

半横向通风；公路隧道；通风压力；理论研究

半横向通风是一种常见的公路隧道机械通风方式，虽然存在施工成本高、难度大等特点，但是在面对火灾情况下的烟气处理问题以及隧道运营条件下的噪声处理问题时，这种通风方式相比于纵向式通风而言会有明显优势。也正因为如此，半横向式通风在奥地利、瑞士等欧洲国家被广泛采 用[1−4]。在国内，采用该通风方式的案例也不在少数[5−6]。送风风机全压与送风风阀开度是半横向通风的关键设计参数。风机全压与风道内始末端静压差有关；风阀开度的设计目的则在于使风量能在隧道内均匀输送，设计时需要明确风道内的静压分布形式[7−8]。相关规范[9]已经给出了送风井位于隧道一端或者两端的风道内静压差求解公式，陈德芳 等[10−11]基于一元流伯努利方程计算得出隧道单位长度需风量保持不变的风道内静压分布形式。然而，对于送风井位于隧道中部，风流朝向两侧流动的半横向通风方式，业界还没有类似的设计案例。另外，对于存在分岔的隧道而言，分岔前与分岔后的区段隧道内交通量会有显著区别，这导致2部分隧道区段的需风量标准会有所不同，目前研究所取得的静压分布公式不能直接应用于该类型风道静压的求解。综上，目前并没有关于送风井位于隧道中部且隧道范围内需风量标准存在分段变化的半横向通风设计方法。在此，以厦门海沧疏港通道−芦澳路地下互通隧道工程为依托，对该特殊形式下的半横向通风方式进行研究，目的在于明确该通风方式下风道内的静压分布形式以及送风风机功率设计方法。研究成果将不仅为依托工程提供理论支撑，同时也会对类似工程修建提供技术参考。

1 工程概况

厦门市海沧疏港通道−芦澳路城市地下立交互通隧道工程是实现厦成高速与港区及厦门本岛与港区之间交通转换的重要交通枢纽工程，该工程由南北走向的芦澳路、东西走向的疏港路以及连接2条主路的A，B，C和D 4条匝道组成。匝道设计通风方式为送风型半横向，送风井采用修建匝道所遗留的施工斜井，该井位于C匝道中间位置。工程示意具体如图1所示。

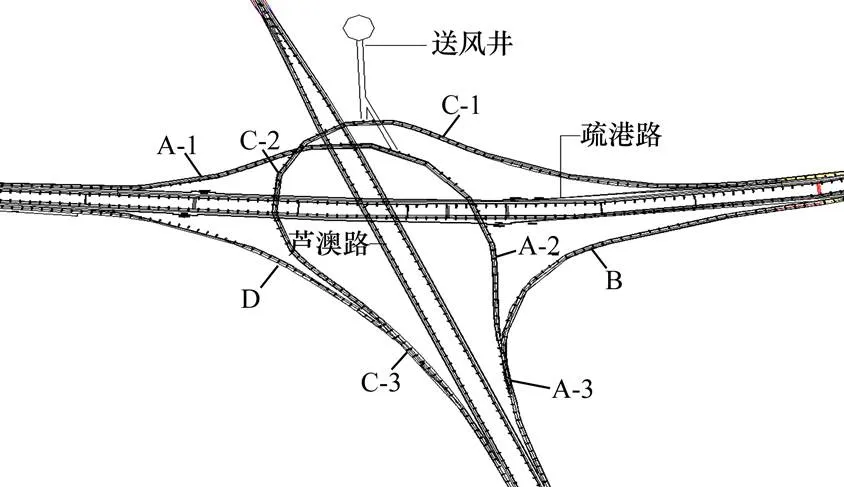
图1 工程示意

送风井经过分岔改造之后分别为A匝道和C匝道送风，两者之间相互独立，互不影响。B和D匝道分别为A和C匝道的分支。示意图对A和C匝道进行了区段的划分，划分节点为匝道分岔点和送风井接入点。匝道断面上方修建了送风道，风道面积为10.8 m2，当量直径为2.54 m。尺寸示意图如图2所示。

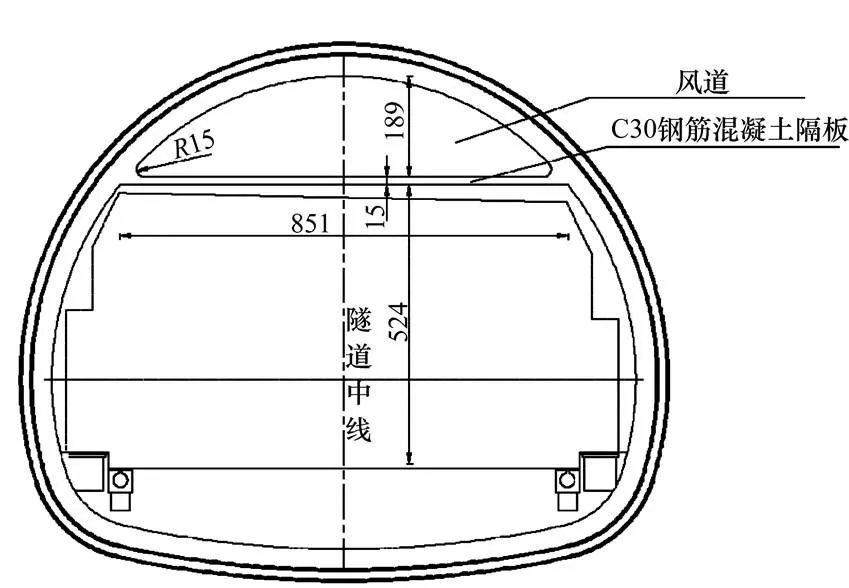
单位：cm

由于送风井接入位置位于匝道中部而不是匝道端口，风流进入风道后会朝向匝道两侧流动。以C匝道为例，风流由斜井进入后，一部分风量朝向疏港路方向流动(C1区段)，另一部分朝向芦澳路方向流动(C2区段)。结合匝道预测交通量以及匝道横断面尺寸等参数对匝道的需风量进行计算，得到的匝道各区段需风量计算结果如表1所示。

由表1可知，由于匝道存在汇合与分岔，C3和A3区段的交通量比其余匝道区段大很多，这也导致这2个区段的单位长度需风量大于其余区段。

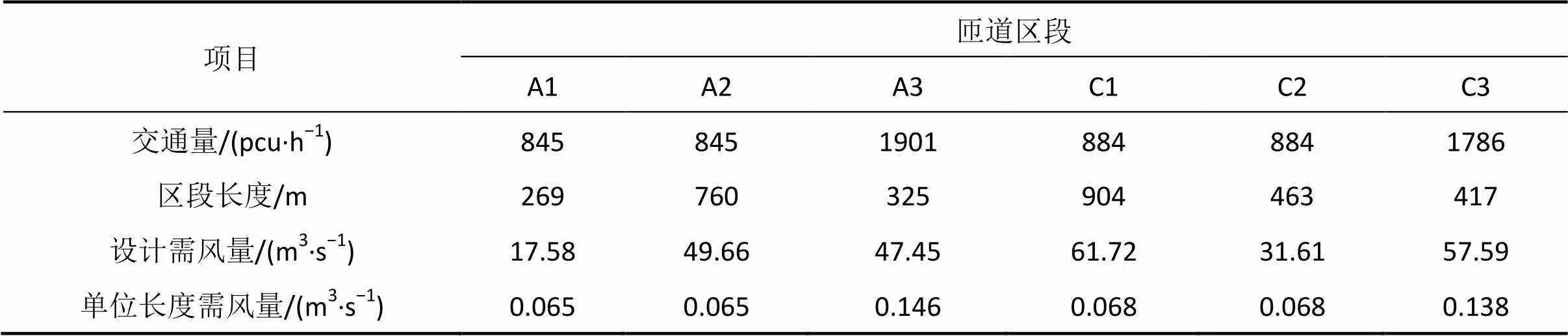
表1 匝道区段划分示意

2 通风方式理论分析

以C匝道为例，对送风井位于隧道中部，隧道内需风量存在分段变化的半横向通风方式进行理论分析。

2.1 风道内风速分布

风流从送风井引入风道，之后经由风阀流入隧道内部，风道范围内风道始端位置产生最大风速，记为v。各区段风道始端的风速可按照下式进行 计算：

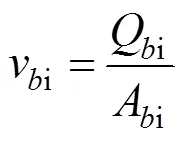
式中：Qi为流经i区段风道始端的风量；Ai为i区段风道横断面面积。

该工程风道面积均设置为10.8 m2。C匝道内各区段风道始端风速见表2。

表2 各区段风速起始风速表

传统单端送风型半横向通风方式中，通过调节风阀可使各风阀流出的风量相等。此时，风流在整个风道范围内线性递减，风道末端风速为0，风道内任意点处的风速与始端风速之间满足如下关 系式：

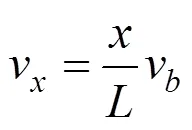
式中：为距离风道末端的距离；v为距离风道末端距离为处的风速。

该工程中，计算时考虑各区段范围内风量满足线性递减的规律。由此可以得到各区段范围内风速分布形式如下。

1) C1区段内风速分布满足关系式：

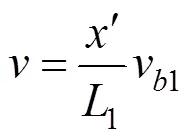
式中：′表示距离C1匝道区段末端的距离；1表示C1区段的长度。

2) C2及C3区段内风速分布满足关系式：

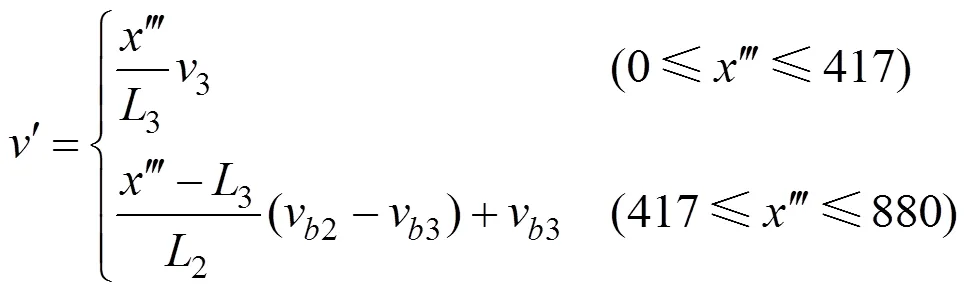
式中：′″表示距离C3区段风道末端的距离。风道内风速具体分布形式如图3所示。

图3 风道内风速分布形式

Fig. 3 Distribution form of flow velocity in air duct

2.2 风道内压力分布

根据匝道内风速分布曲线将匝道所划分的3个区段分为2类，一类区段末端风速为零，如C1与C3区段；另一类区段末端风速不为零，如C2区段。

2.2.1 末端风速为0区段风道静压分布求解

隧道内的流动空气密度变化较小，且符合连续介质假设，可以考虑为理想流体[12]。风道送风过程中可以将风道视为主管，风孔视为支管，主管与主管间、主管与支管间流线始终保持连续性，因此可以将伯努利方程应用于总流与支流管路之间。对于末端分速为0的区段，通过对风道末端和风道内任意断面建立总流伯努利方程可以实现对风道内任意位置处静压的求解。风道内风流示意如图4所示。

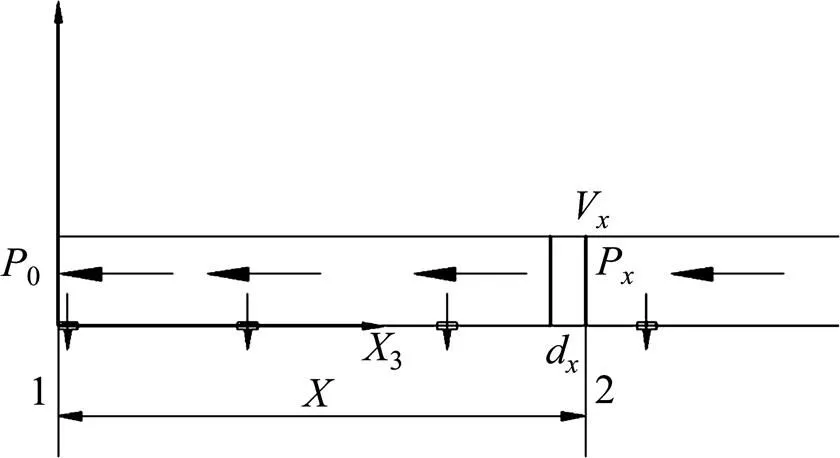
图4 风道内风流示意

取1和2断面建立伯努利方程：

式中：1为风道末端静压；2为断面2的静压；h为风流从断面2流至断面1所产生的压力损失。压力损失来源于2个部分，分别是风流沿风道粗糙内壁流动产生的沿程阻力损失和风流流经风阀处产生的局部阻力损失，后者类似于三通管中的直通损失相较于第1部分很小，可以忽略[13]。由于2个断面高差较小，计算忽略两端的势能差时式(5)可以变形为：

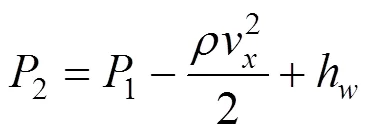
取微段d进行沿程损失分析，微段内的沿程损失为：

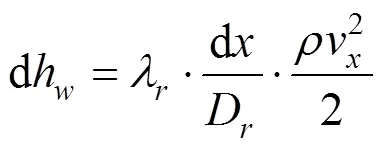
式中：D为主风道当量直径；为距区段末端距离；为主风道沿程阻力系数，该值由风道平均壁面粗糙度Δ确定。

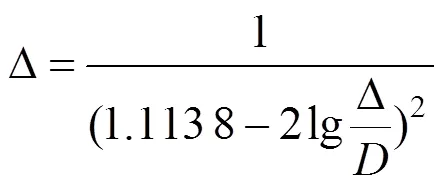
风道内壁面由混凝土制造，平均粗糙高度可取为3 mm，沿程阻力系数计算为0.021。容易求得区段内任意点处的静压2为：

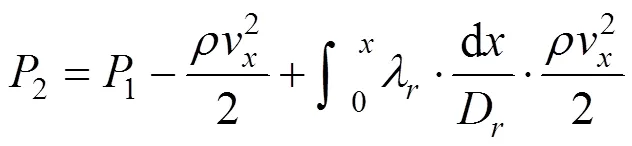
将v与风道始端风速v之间的关系式代入上式，可以推导得风道末端风速为0的风道内静压分布公式为：

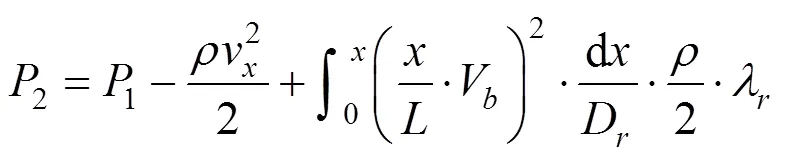
化简后为：

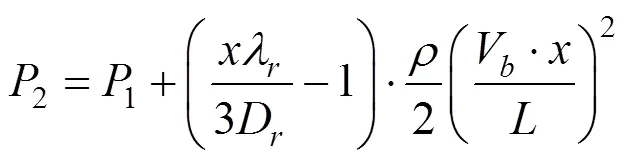
本工程中，C1区段风道末端风速为0，其风道内静压分布公式可以采用该式进行计算。当不考虑C2与C3区段对该区段的静压影响时计算可首先确定其末端静压1。参照《公路隧道通风设计细则》，为保证风道送风量分布的均匀性，该值通常取为150 N/m2。计算得到的风道内静压分布形式如图5所示。

图5 C1区段风道静压分布曲线

Fig. 5 Theoretical calculation results of static pressure in C1 duct section

根据图5，满足C1区段送风需求时，风道始端静压应为178.93 Pa，风道内最大静压差为28.93 Pa。

C3区段末端风速为0，该区段内静压求解方法与C1区段相同。取末端静压为150 Pa时，求解公式如下：

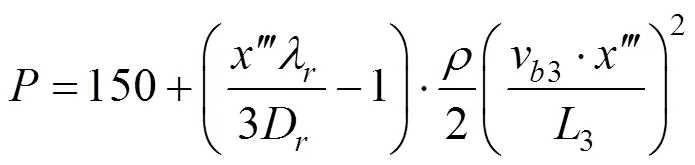
求得的风道区段始端静压为152.22 Pa，静压差降为2.22 Pa。

2.2.2 末端风速不为0区段风道静压分布求解

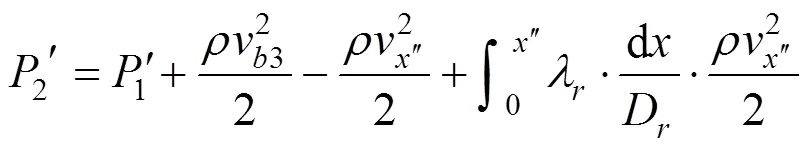
式中：″表示距离C2区段的距离。根据C2与C3区段内的风速分布曲线可知该部分风道内风速分布形式为一条折线，由2条斜率不同的直线组成，令C3区段内风速曲线斜率为3，C2区段内风速斜率为2，那么C2区段内风速分布公式可由下式 表达：

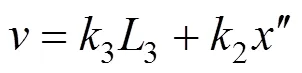
将该式代入C2区段内静压求解公式并化简 可得：

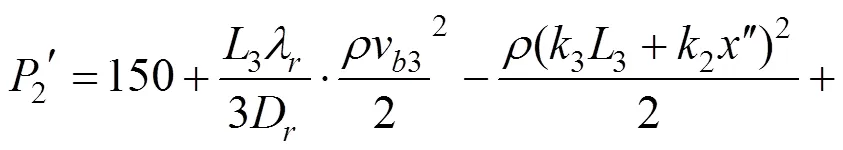
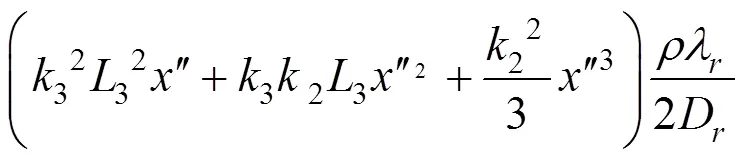
仅考虑C2与C3区段的送风需求时，风道内的静压分布计算结果如图6所示。

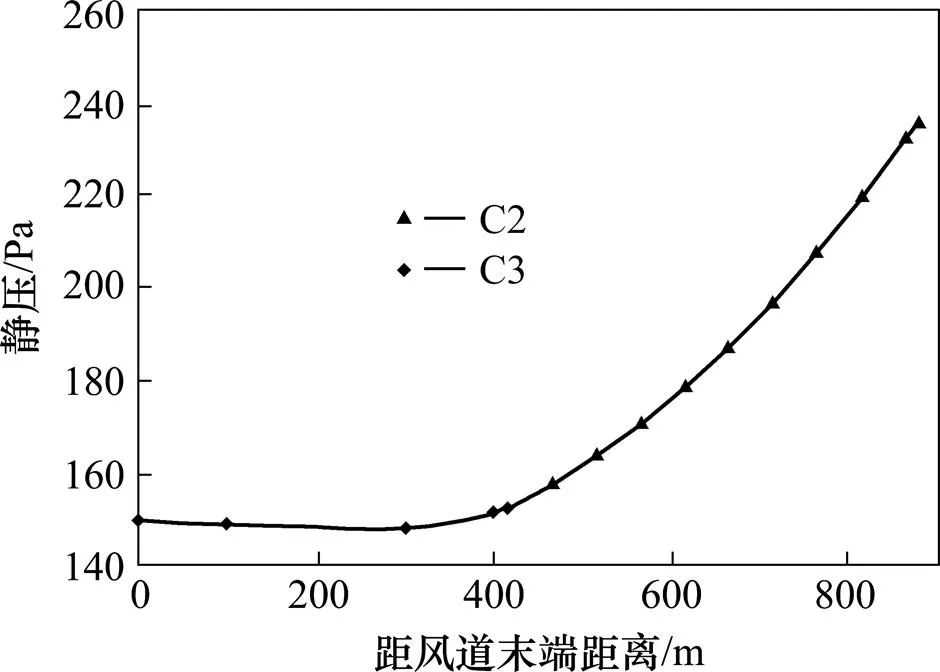
图6 C2及C3区段风道静压分布曲线

C2区段风道始端静压应为235.6 Pa，风道内最大静压差降为85.6 Pa。

2.2.3 风道内静压分布形式确定

前面求解得出的区段内静压分布曲线并没有考虑区段间的相互影响与联系。在该工程中，风流由送风井进入后朝向风道两侧流动，具体如图7 所示。

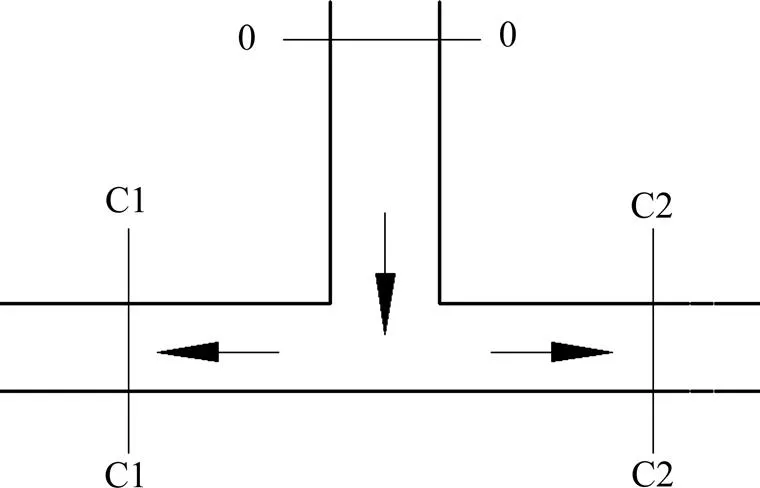
图7 区段间风流关系示意

3个断面间应满足如下关系：

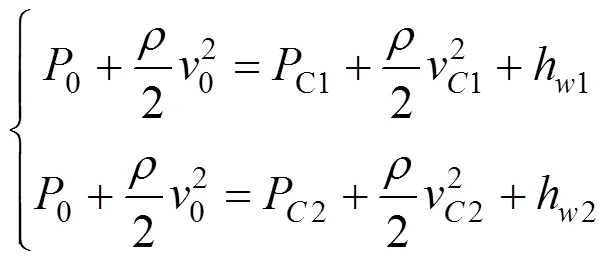
也即：

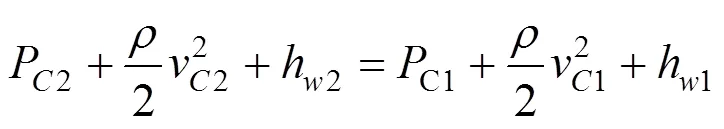
实际施工时通过在风井接入口位置设置相应导流措施可以减小该位置处由风流转向所引起的压力损失h。当不考虑该部分损失时，C1与C2区段始端全压应相等，两者之间静压差即为动压差。代入2区段始端风速容易计算得该差值为21.2 Pa。

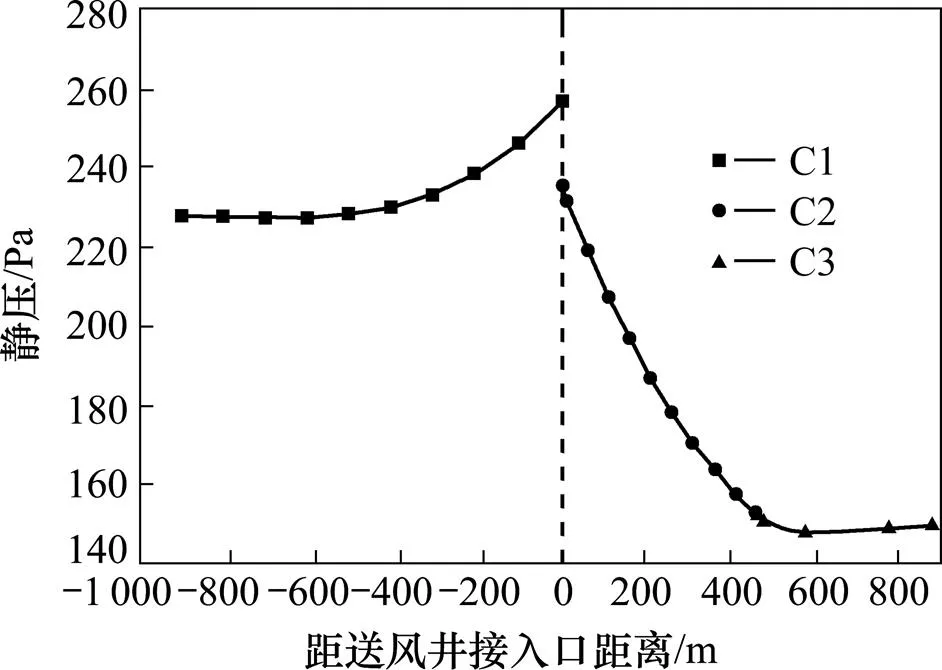
图8 理论计算风道静压分布曲线

考虑到C2区段送风所需压力大于C1区段，送风井接入位置静压应首先满足C2区段始端静压要求。因此将C1区段始端静压修正为256.8 Pa。最终得到的整个匝道范围内的静压和全压分布形式分别如图8和图9所示。

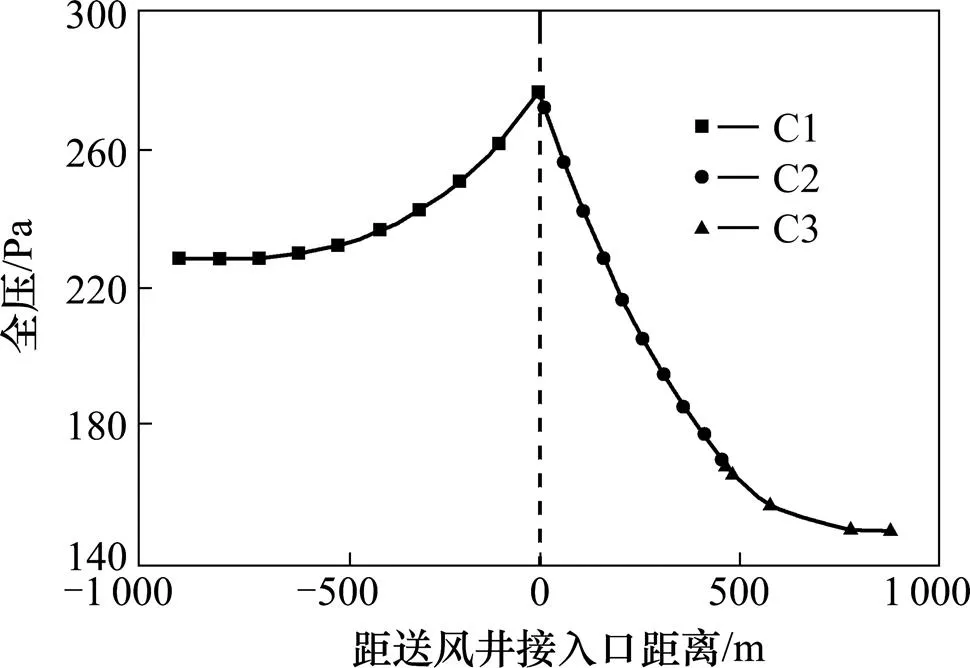
图9 理论计算风道全压分布曲线

3 数值分析验证

为验证理论计算结果的准确性，利用FLUENT建立三维数值模型对该隧道送风方式进行模拟。三维模型如图10所示。

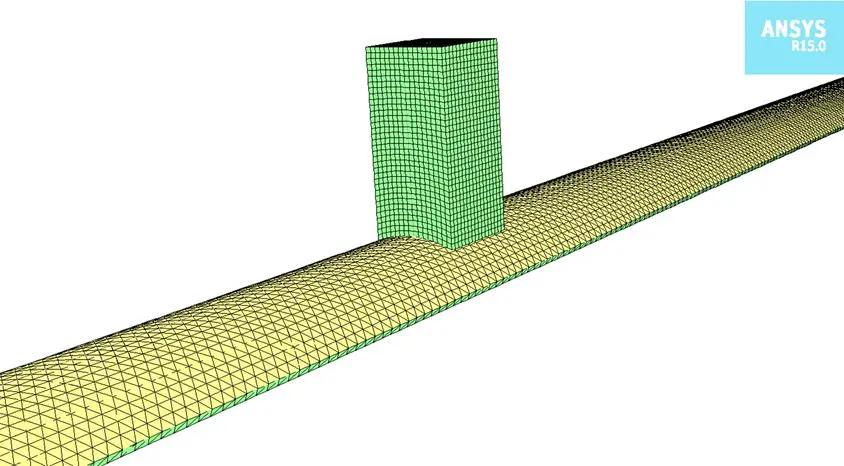
图10 数值分析模型

1) 模型断面及长度尺寸按照工程实际建立；

2) 风道壁面设置为非滑移wall边界，壁面平均粗糙高度取为3 mm[14]；

3) 风道内按20 m间距设置1 m2的风阀，风阀设为velocity-inlet边界；

4) 计算采用湍流模型为−(real)。

计算时通过控制风阀风速实现各区段内风量的均匀输送。当C3区段末端静压为150Pa时，数值计算与理论计算所得到的风道内静压和全压对比结果分别如图11和图12所示。

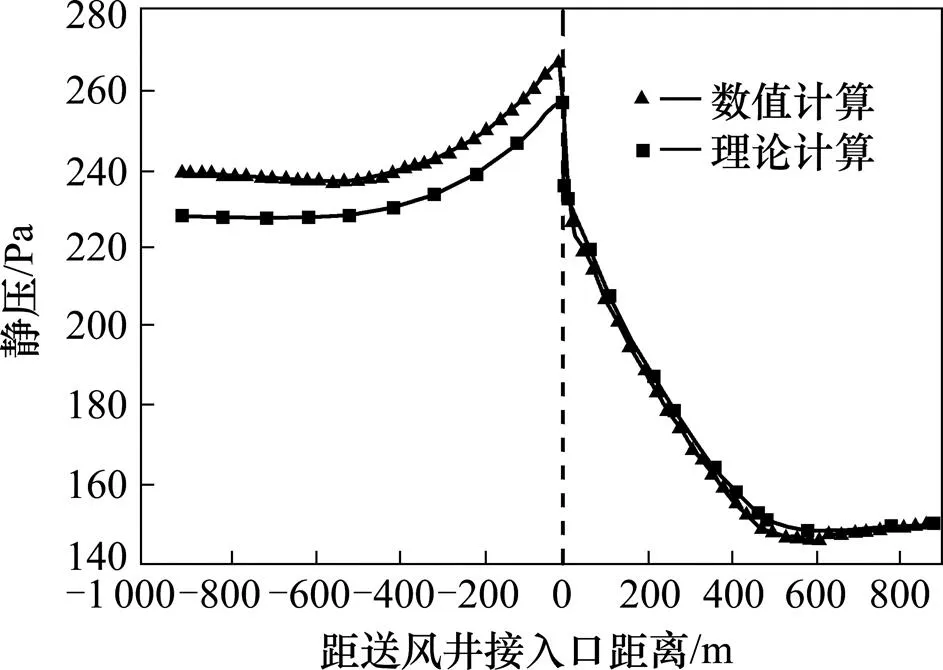
图11 风道静压分布对比曲线

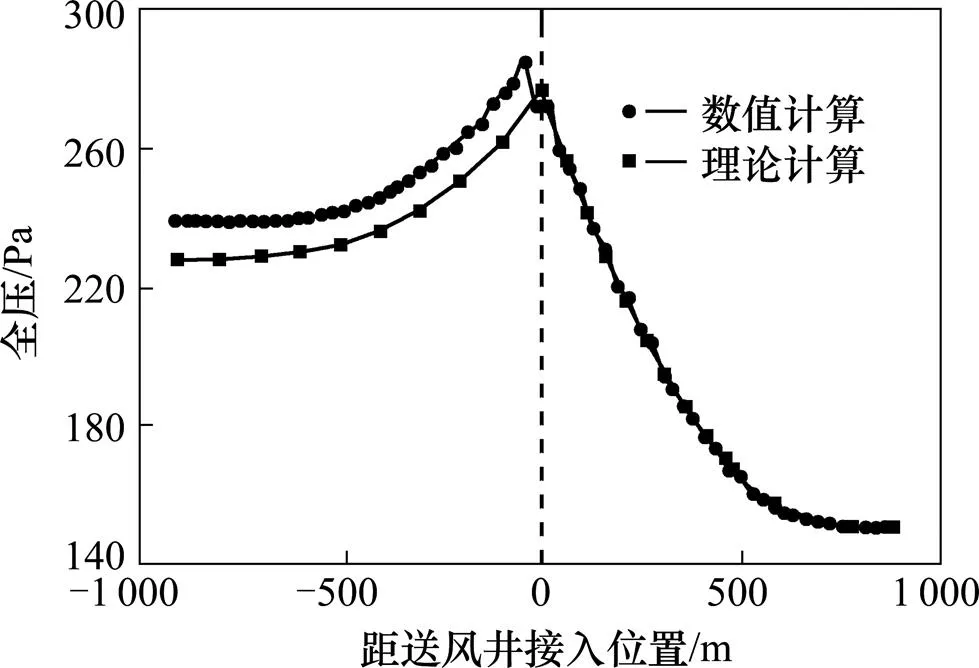
图12 风道全压分布对比曲线

根据图12，数值计算得到的C2和C3区段静压分布与理论计算结果基本吻合，C1区段内静压分布大于理论计算结果，二者之间差值约为11 Pa。这是由于理论计算中没有考虑风流转向所引起的压力损失所导致的。然而从计算结果来看，由于C2一侧风速较大，因此产生的压力损失相比C1一侧要大，但是差值与风道始端全压相比较小，仅为后者的4.3%。同时，考虑到施工时施作相应导流措施的情况下该值可能更小，因此将送风井两端全压视为相等是可行的。也即表明该通风方式下，风机提供全压在满足通风压力较高的C2与C3区段时，C1区段通风需求也能满足。

4 送风井位置对风机压力的影响分析

半横向通风中，风机需要提供的全压包括风道内的静压差、风道始端动压、风道末端静压以及连接风道内的压力损失。前面3部分压力是风流在风道范围内流动所必需的。本工程中该部分压力为：

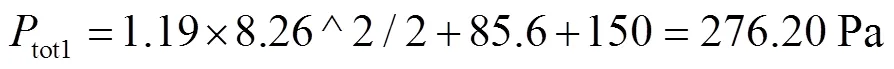
为分析该隧道送风井设置方式在减小风机压力方面的优势，对送风井位于隧道C1和C3末端的情况进行风道压力分析。各情况下的送风井位置对比情况如图13所示。

图13 送风井位置布置示意图

Fig. 13 Schematic diagram of different inclined locations

1) 送风井位于C1末端

当送风井位于C1末端，风道内风速分布形式如图14所示。

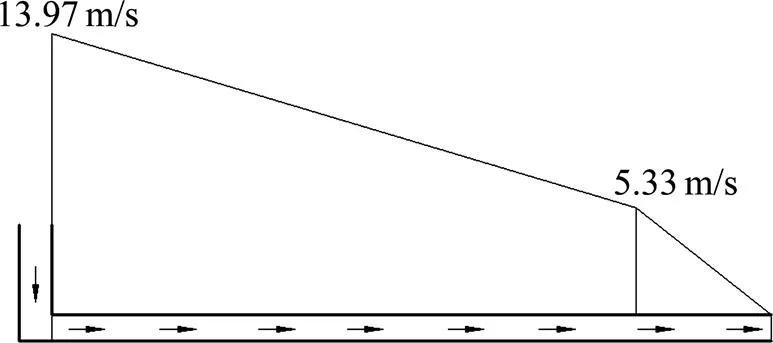
图14 送风井位于C1端时风道内的风速分布曲线

将风速分布曲线代入前面推导得到的静压求解公式后计算得到的风道始端静压为721 Pa，风道内最大静压差为571 Pa，静压分布曲线如图15 所示。

该送风方式下风道内流动所需风机压力为：

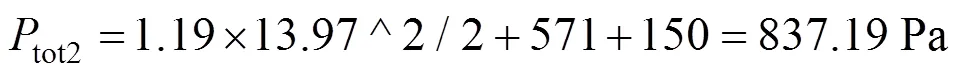
2) 送风井位于C3末端

当送风井位于C3末端，风道内风速分布形式如图16所示。

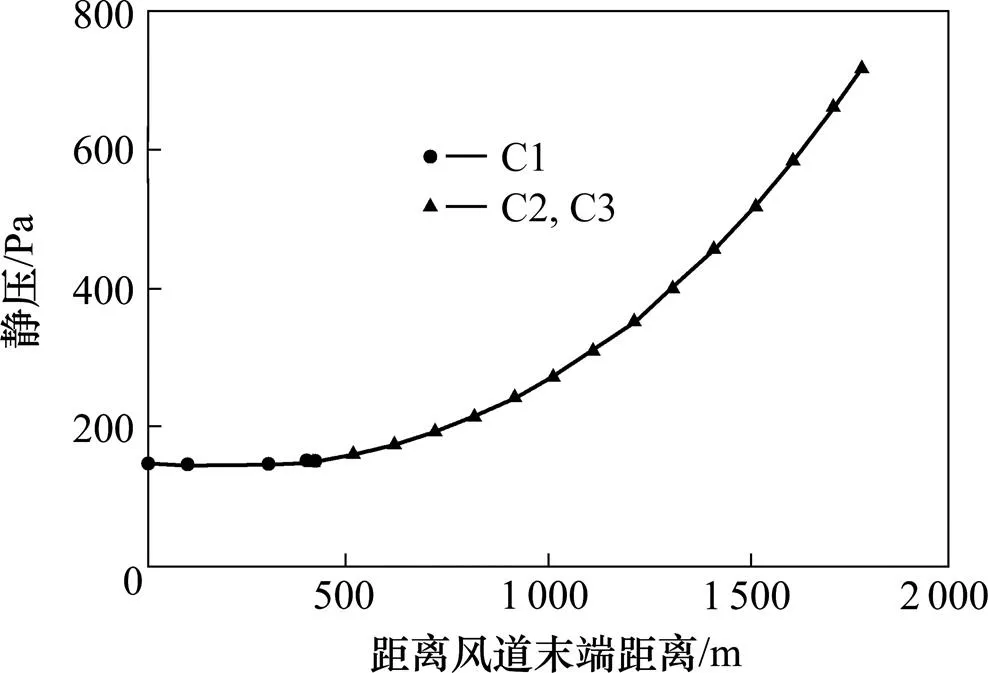
图15 送风井位于C1端时风道内的静压分布曲线

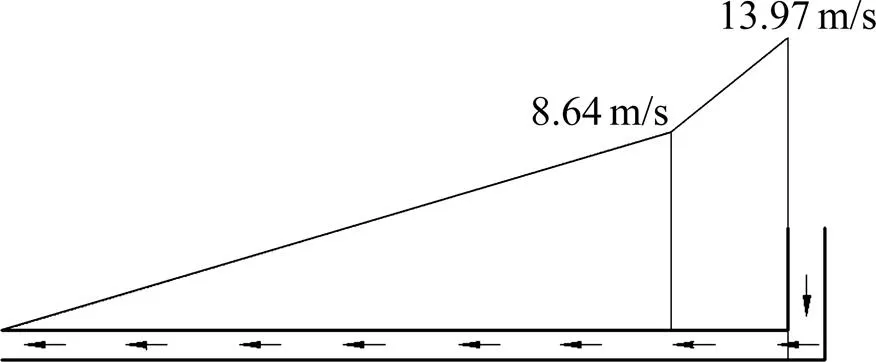
图16 送风井位于C3端时风道内的风速分布曲线

经计算，该送风方式下风道始端静压为468 Pa，风道内最大静压差为318 Pa，静压分布曲线如图17所示。

该送风方式下风道内所需风机压力为：

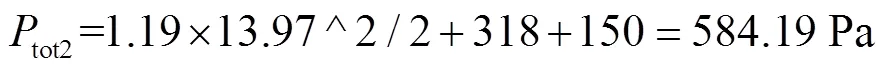
3种送风方式下风道范围内所需风机对比结果如表3所示。

根据表3，该工程将送风井设置于隧道中部位置时风道范围内所需风机压力仅为2种单端送风方式的32.5%和46.5%，节省的风机功率约为85.1 kW和46.9 kW。由于通风阻力与风速的平方和通风距离成正相关，送风井设置于隧道中间时不仅缩短了通风距离，单侧风道的送风风速也相应减小，由此带来的风机压力及功率折减将超过单端送风方式的50%。因此，送风井位于隧道中部的半横向通风方式在通风长度的适应性以及减小运营成本方面较单端送风方式而言有明显优势。

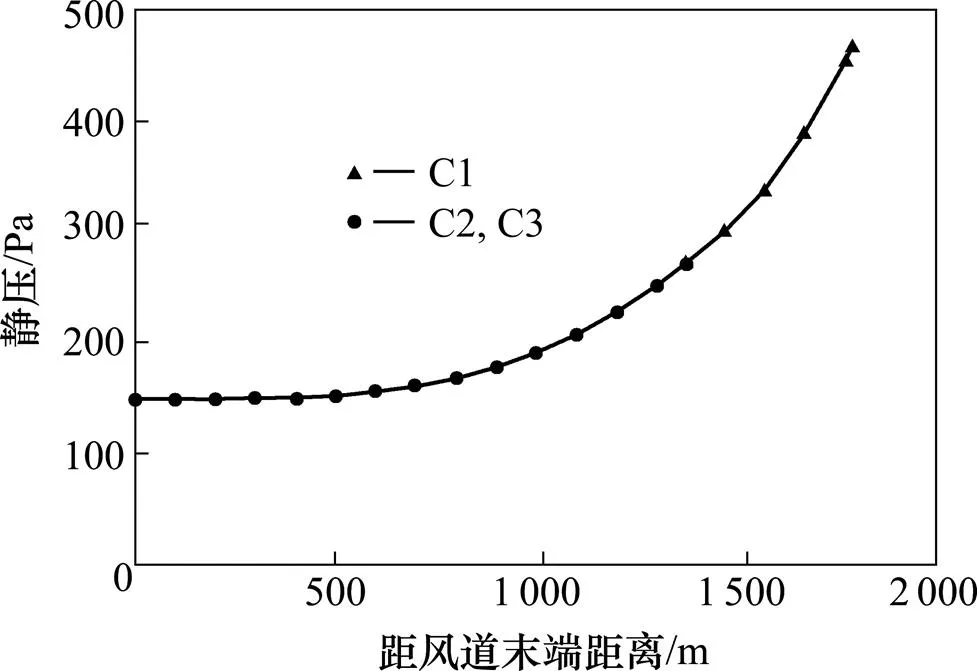
图17 送风井位于C3端时风道内的静压分布曲线

表3 风机压力对比表

5 结论

1) 建立风道末端风速为0和不为0 2种情况下风道内的静压分布计算公式，适用于求解隧道内需风量分段变化情况下的风道内静压分布。

2) 送风井从隧道中部送风时送风井接入位置两侧风道始端全压可视为相等，因此，送风机只需提供满足通风压力需求较大一侧的全压即可实现整个隧道的有效通风。

3) 送风井位于隧道中部不仅缩短了有效通风距离，单侧风道的送风风速也相应减小。该通风方式在增大通风长度适应性、减小风机功率及提高经济性方面有显著优势。

[1] 储诚赞, 刘玉新, 燕凌. 公路隧道节能方式探究[J]. 现代隧道技术, 2016, 53(1): 23−27. CHU Chengzan, LIU Yuxin, YAN Ling. On the energy-saving mode for highway tunnels[J]. Mordern Tunnelling Technology, 2016, 53(1): 23−27.

[2] Choi J S, Kim M B, Choi D H. Experimental investigation on smoke propagation in a transversely ventilated tunnel[J]. Journal of Fire Sciences, 2005, 23(6): 469−483.

[3] LI J S M, Chow W K. Numerical studies on performance evaluation of tunnel ventilation safety systems[J]. Tunneling & Underground Space Technology Incorporating Trenchless Technology Research, 2003, 18(5): 435−452.

[4] Lesser N, Horowitz F, King K. Transverse ventilation system of the Holland tunnel evaluated and operated in semi-transverse mode[J]. Transportation Research Record, 1987.

[5] 《中国公路学报》编辑部. 中国隧道工程学术研究综述·2015[J]. 中国公路学报, 2015, 28(5): 1−65. Editorial Department of China Journal of Highway and Transport. Review on China's tunnel engineering research: 2015[J]. China Journal of Highway and Transport, 2015, 28(5): 1−65.

[6] 王亚琼, 谢永利, 刘洪洲, 等. 海底隧道半横向通风孔物理模型试验[J]. 中国公路学报, 2010, 23(3): 76−82. WANG Yaqiong, XIE Yongli, LIU Hongzhou, et al. Physical model experiment on semi-transverse ventilation air inletand outlet of subsea tunnel[J]. China Journal of Highway and Transport, 2010, 23(3): 76−82.

[7] JoH J, Min K M, Daiki Min, et al. A fundamental study for optimizing the supply and exhaust port opening ratio in road tunnels with transverse ventilation system[J]. Journal of the Korean Society of Mineral and Energy Resources Engineering, 2016, 53(2): 140−145.

[8] Hyeong-Je Jo, Kyu-Myung Chun, Dea-Kee Min, et al. A study on the program development for optimizing the supply and exhaust port opening ratio in road tunnels with transverse ventilation system[J]. Journal of Korean Tunneling and Underground Space Association, 2017, 19(3): 517−532.

[9] JTG/T D70/2−02−2014, 公路隧道通风设计细则[S]. JTG/T D70/2−02−2014, Guidelines for design of ventilation of highway tunnels[S].

[10] 陈德芳. 半横向通风方式分析研究和计算[J]. 地下工程与隧道, 1996(2): 24−35. CHEN Defang. Study on semi-transvers ventilation[J]. Underground and Tunnel Engineering, 1996(2): 24−35.

[11] 夏永旭, 赵峰. 特长公路隧道纵向−半横向混合式通风方式研究[J]. 中国公路学报, 2005, 18(3): 80−83. XIA Yongxu, ZHAO Feng. Research on the combined longitudinal and semi-transverse ventilation system in lengthy highway tunnels[J]. China Journal of Highway and Transport, 2005, 18(3): 80−83.

[12] 刘健. 隧道通风安全与照明[M]. 重庆: 重庆大学出版社, 2015. LIU Jian. Tunnel ventilation safety and lighting[M]. Chongqing: Chongqing University Press, 2015.

[13] 石喜, 吕宏兴, 朱德兰, 等. PVC三通管水流阻力与流动特征分析[J]. 农业机械学报, 2013, 44(1): 73−79. SHI Xi, LÜ Hongxing, ZHU Delan, et al. Flow resistance and characteristics of PVC tee pipes[J]. Transactions of the China Society for Agricultural Machinery, 2013, 44(1): 73−79.

[14] 张恒, 林放, 孙建春, 等. 基于典型壁面粗糙模型的隧道施工通风效果CFD分析[J]. 中国铁道科学, 2016, 37(5): 58−65. ZHANG Heng, LIN Fang, SUN Jianchun, et al. CFD analysis of tunnel construction ventilation effect based on typical roughness model[J]. China Railway Science, 2016, 37(5): 58−65.

Characteristic study of a sectionalized semi-transverse ventilation system in which inclined shaft is built at the middle of the tunnel

WANG Mingnian1, ZHANG Jianbin2, DENG Tao1, YU Li1, WANG Xu1

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Xiamen Road & Bridge Construction Investment Development Co., Ltd, Xiamen 361009, China)

In this paper, a special form of semi-transverse ventilation applied in Xiamen Shugang-Luao underground overpass was studied. Different from ordinary ones, inclined shaft was built at the middle of the tunnel and the requirement of fresh air per meter along this tunnel is not constant in this ventilation. According to the fresh air requirement standard per meter, air duct was divided into different sections. Based on an assumption that air was evenly supplied in each section, flow rate of the air duct was obtained. With energy conservation equations built between the cross sections internal and at the end of duct sections, two formulas for calculating static pressure along the air duct were derived and the theoretical calculations was verified with numerical results. In this kind of ventilation, air flow from the inclined shaft separates into two directions and research reveals that the two sections nearly have same total pressure at the separation point, which leads to a great reduction of fan power when compared with those in which shaft built at the end of a tunnel.

semi-transverse ventilation; road tunnel; ventilation pressure; theoretical research

10.19713/j.cnki.43−1423/u.2019.04.019

U453.5

A

1672 − 7029(2019)04 − 0976 − 08

2018−04−24

国家自然科学基金资助项目(51308472)

于丽(1978−)，女，辽宁大连人，副教授，博士，从事隧道及地下工程方面的研究与教学工作；E−mail：yuli_1026@ swjtu.edu.cn

(编辑 阳丽霞)