2类PBL推出试验破坏机理及承载力影响因素研究

施洲，秦搏聪



2类PBL推出试验破坏机理及承载力影响因素研究

施洲，秦搏聪

(西南交通大学 土木工程学院，四川 成都 610031)

为探明2类PBL推出试验的破坏机理及极限承载力的主要影响因素，基于Abaqus平台运用非线性有限元方法建立2类PBL推出试验的精细有限元模型。计算结果表明：PBL在埋入式试验中的极限承载力与滑移性能均优于标准推出试验，非线性有限元计算结果与试验结果符合较好。2类推出试验的破坏机理及主要构件的破坏形态差异较大，标准推出试验中试件的破坏源于混凝土开裂，而埋入式试验则是由于贯通钢筋被剪断。参数分析表明：在标准推出试验中，PBL极限承载力主要与混凝土强度和开孔板孔径有关；在埋入式试验中，混凝土强度、开孔板孔径和贯通钢筋直径对PBL极限承载力均有较大影响。

PBL剪力键；推出试验；Abaqus；破坏机理；参数分析

钢−混组合结构充分发挥了钢与混凝土2种材料的优点，在当下桥梁工程朝着轻质、高强、大跨目标发展的背景下，钢−混组合桥梁特别是铁路钢混组合桥梁发展十分迅速。剪力键是钢−混组合桥梁共同工作的基础和关键构造之一，其中PBL剪力键(简称PBL)是目前组合桥梁中运用极为广泛的剪力键，PBL的试验方法、极限承载力等特性对组合结构而言至关重要，国内外学者曾对其开展过广泛的研究。Kim等[1]通过计算研究提出PBL剪力键群极限承载能力折减系数的概念，给出了折减系数为0.8的计算公式。Valente等[2]进行了8组PBL推出试验，对贯穿钢筋、混凝土的承压效应进行了研究。Kim等[3]对10个翼缘板为波形钢的PBL进行了推出试验，研究表明波形钢的形状影响PBL的承载力，贯通钢筋可增大PBL的承载力和滑移量峰值。Vianna等[4]通过11组PBL推出试验得出，随着开孔数目增加，PBL的刚度增加较小，而极限承载力呈线性增加。曹学亮等[5]利用Abaqus建立PBL有限元模型，将计算与试验数据对比，验证了推出试验数值模拟方法的可行性。张清华等[6]研究了PBL剪力键群的传力机理及极限承载力，探讨了PBL剪力键群的设计理念和方法。胡建华等[7]利用15组PBL试验进行极限承载力试验，研究了PBL极限承载力的各种影响因素，开孔板孔径、贯通钢筋和混凝土是影响其极限承载力的主要因素。肖林等[8]设计并制作了2类试验构造的推出试验，试验结果表明PBL在钢−混结合段中的抗剪性能优于钢−混叠合梁。石宵爽等[9]利用4个PBL推出试验，分析了腹板厚度和开孔大小对PBL承载力和破坏机理的影响。汪维安等[10]通过PBL剪力键群推出试验，提出了PBL剪力键群承载力的计算方法和正常使用极限荷载的指标。可见，PBL的理论与试验研究主要是通过推出试验进行，其原因有二，一是相较于梁式试验，推出试验试件制作方便，成本低廉；二是由推出试验得到的PBL抗剪承载力低于梁式试验，按照推出试验得到的结果进行设计偏于安全。目前，主要有2种构造形式的推出试验，一类为标准推出试验，标准推出试验对于叠合梁具有较好的效果，Eurocode 4给出了剪力键标准推出试验的试验方法；另一类由于外围混凝土块较厚且剪力键埋入较深，因此被称为埋入式试验[12]，首先用于南京三桥钢−混结合段试验[11]效果良好，而后被逐渐应用于混合梁、混合桥塔等新型结构中，在此种推出试验与标准推出试验中，PBL的受力状态存在明显差异[11]；标准推出试验适用于叠合梁中的剪力键；而在埋入式试验中PBL深埋于外围混凝土中，使其受到了较强的界面约束，它的破坏形态与叠合梁剪力键具有较大不同[13]。为深入研究2类PBL推出试验的破坏机理和极限承载力影响因素，基于Abaqus平台建立2类PBL推出试验的三维精细有限元仿真模型，对其进行对比分析。

1 有限元分析

1.1 非线性有限元方法

实体推出试验存在着几何、材料与接触状态3类非线性问题，应采用非线性有限元法对其进行分析。非线性有限元法是用计算机求解非线性问题的数值计算方法，较之于实体推出试验其成本低廉，不受场地、材料离散型及其他意外因素的影响，在设置了合理的模型参数(包括材料本构、网格、接触、加载)的条件下，非线性有限元法能够较为准确地模拟推出试验的加载全过程，真实地反映结构的加载历程和受力状态。

1.2 有限元模型建立

2类PBL推出试验的主要构件包括混凝土部分(混凝土块、混凝土榫)与钢结构部分(开孔板、贯通钢筋、钢梁、箍筋)。有限元模型分为P1与P2 2类，其几何尺寸及材料特性参照文献[8]中的ST16及PT16试件，分别对应典型的PBL标准推出试验与埋入式试验(以下分别简称为标准试件与埋入式试件)，2类推出试验的构造如图1所示，详细的模型及试件尺寸见表1。

混凝土的本构模型采用混凝土塑性损伤模型，在混凝土塑性损伤模型中可通过计算损伤因子折减刚度矩阵，以此模拟混凝土单元的刚度下降或失效；混凝土的受拉与受压应力−应变曲线图如图2所示。

混凝土弹性数据中，弹性模量取34.5 GPa，泊松比取0.2；塑性数据中，膨胀角取30°，偏心率取0.1，b0/c0取1.16，取0.666 7，黏性参数取0.005[14][15]；钢构件的强度准则采用Von Mises屈服准则；贯通钢筋采用HRB335，钢板采用Q345；钢材的本构关系采用三折线本构模型，应力−应变关系为：

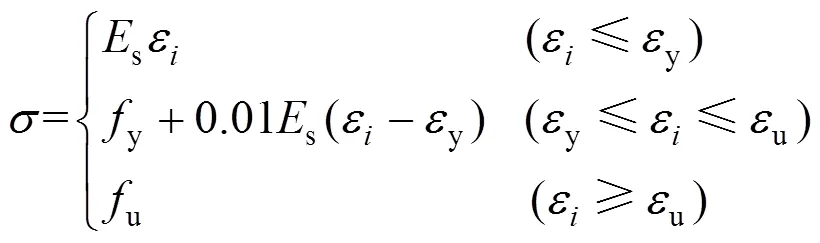
式中：为钢材的等效应力；为钢材的等效应变；y为钢材的屈服强度；u为钢材的极限强度；s为钢材的弹性模量。

箍筋采用三维桁架单元T3D2，其他构件均采用线性减缩积分实体单元C3D8R。在开孔板与混凝土、钢梁交界区域采用单元尺寸为0.5 cm的加密网格，其他区域采用单元尺寸为3 cm的稀疏网格。

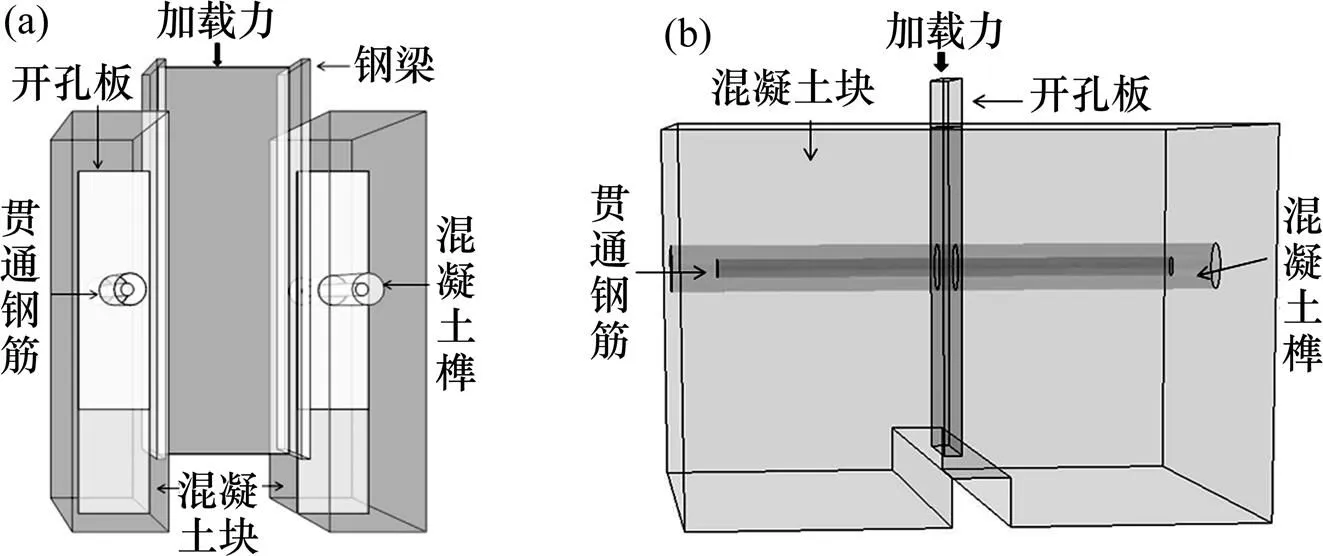
(a) PBL标准推出试验；(b) PBL埋入式试验

表1 试件分类及构造尺寸

(a) 混凝土受拉应力−应变曲线图；(b) 混凝土受压应力−应变曲线图

开孔板与钢梁、混凝土榫与混凝土块、贯通钢筋与混凝土榫之间均采用绑定约束模拟两者的连接。混凝土榫与开孔板、钢与混凝土板之间的接触效应采用2部分模拟：法线方向均采用硬接触，切线方向分别采用摩擦因数为0.904和0.1的罚函 数[16]；箍筋与混凝土采用嵌入约束。采用增量迭代法进行位移加载并设置几何非线性功能对非线性方程组的求解。考虑到接触非线性可能导致的收敛困难，建立一个初始荷载步，对加载面施加足够小的位移以使各个接触对建立起稳定接触关系，在随后的荷载步中进行正常的位移加载。P1模型取半结构建模并在对称面上施加对称边界条件；P2模型取整个结构进行建模。详细的网格划分、构件相互作用及边界条件情况见图3。

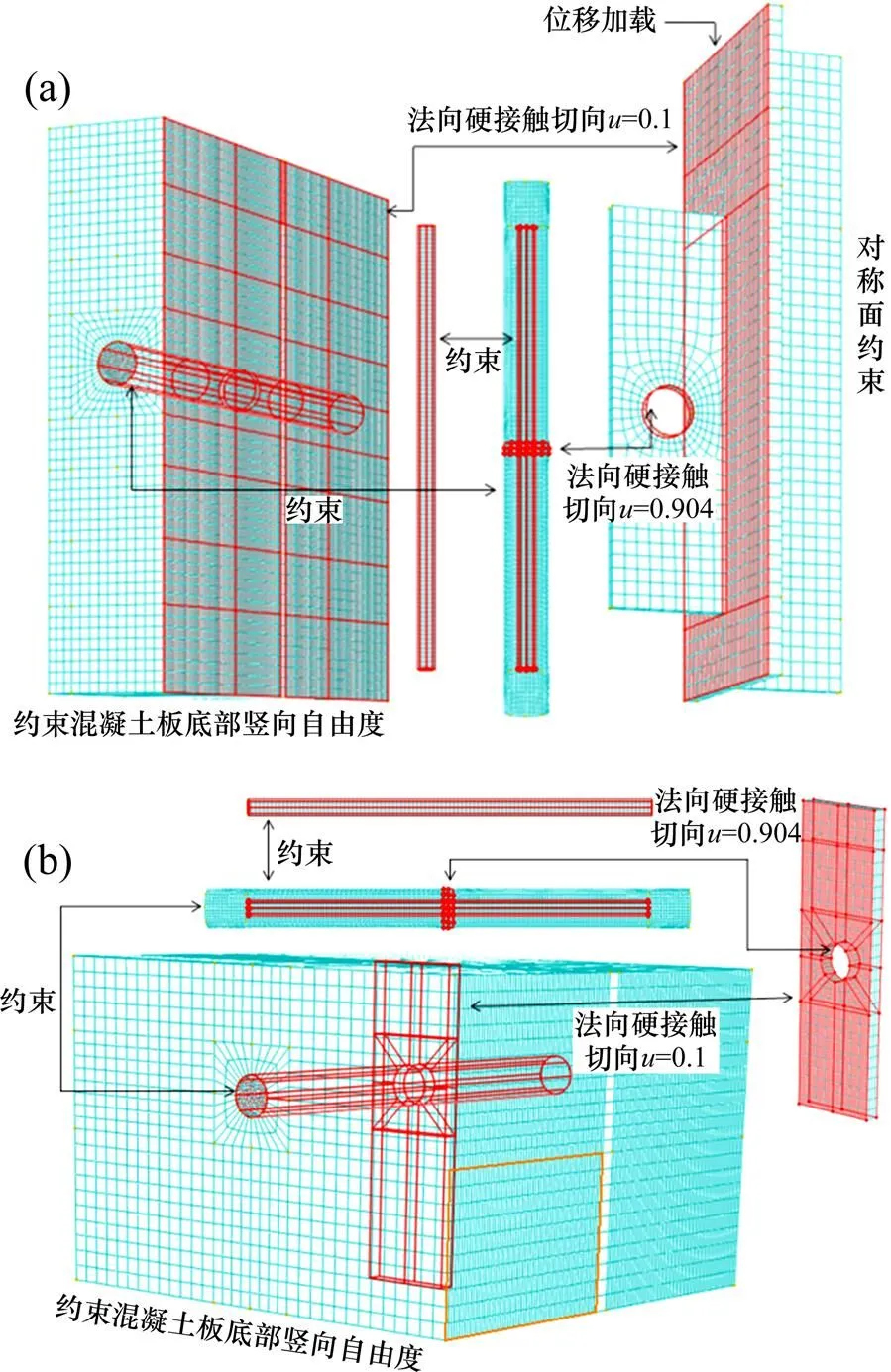
(a) P1模型；(b) P2模型

2 PBL推出试验破坏机理分析

2.1 荷载−滑移曲线

剪力键的荷载−滑移曲线在宏观上表征了剪力键在加载全过程的刚度特性[16]。2类试件中，单孔PBL荷载−滑移曲线的试验值及有限元计算值如图4所示。

图4 PBL荷载-滑移全过程曲线

由图4可见，相同参数的PBL在不同构造的推出试验中，其荷载−滑移曲线差别较大。在标准试件中，PBL的荷载−滑移曲线由上升段和下降段构成，在试件达到极限承载力之后，出现下降段；在埋入式试件中，PBL的荷载−滑移曲线则无下降段，但在屈服之后承载力仍有较大幅度的提高。此外，在埋入式试件中，PBL的极限承载力与滑移量均大于标准试件。2类试件的荷载−滑移曲线均有屈服平台，但埋入式试件的屈服平台及滑移量均大于标准试件，表明PBL在埋入式试验中的延性要优于标准推出试验。此外，由图4对比分析可知，有限元与试验方法得到的荷载−滑移曲线较为吻合，且具有相似的特征。

2.2 PBL抗剪性能指标对比分析

PBL的荷载−滑移曲线表征其宏观上的抗剪性能，其抗剪性能可以通过相应的抗剪性能指标进行评定，表2列出了Eurocode 4对剪力键抗剪性能指标的评定指标，表3列出了PBL的抗剪性能指标的计算值与试验值，综合对比分析可知：非线性有限元方法得到的PBL抗剪性能指标值与试验结果符合得较好，有限元计算值与试验值相差不大且最大差值在5%左右；由前节分析可知，非线性有限元方法与试验方法得到的荷载-滑移曲线较为吻合且具有相似的特征，表明非线性有限元方法可以较好地模拟PBL推出试验。有限元计算值略小于试验值，造成这种情况的主要原因在于：有限元模型中除箍筋外均采用了线性减缩积分单元C3D8R，该单元能够较好地适应大变形及非线性接触等问题的计算分析，然而该单元在扭曲较大时会产生“沙漏问题”，导致其刚度略小于实际值，进而使得有限元计算值偏低。

表2 Eurocode 4对剪力键力学性能指标的评定指标

表3 PBL抗剪性能指标

2.3 2类推出试验的破坏过程与形态

通过实体推出试验能得到PBL的荷载−滑移曲线、抗剪性能指标等宏观特征，而贯通钢筋、混凝土榫等构件的逐步受力过程、应力变化规律等微观力学特征仅能通过有限元模拟来进行研究。通过分析2类试件中主要构件的应力及变形结果，对2类PBL推出试验的破坏过程与形态进行研究。

2.3.1 混凝土部分

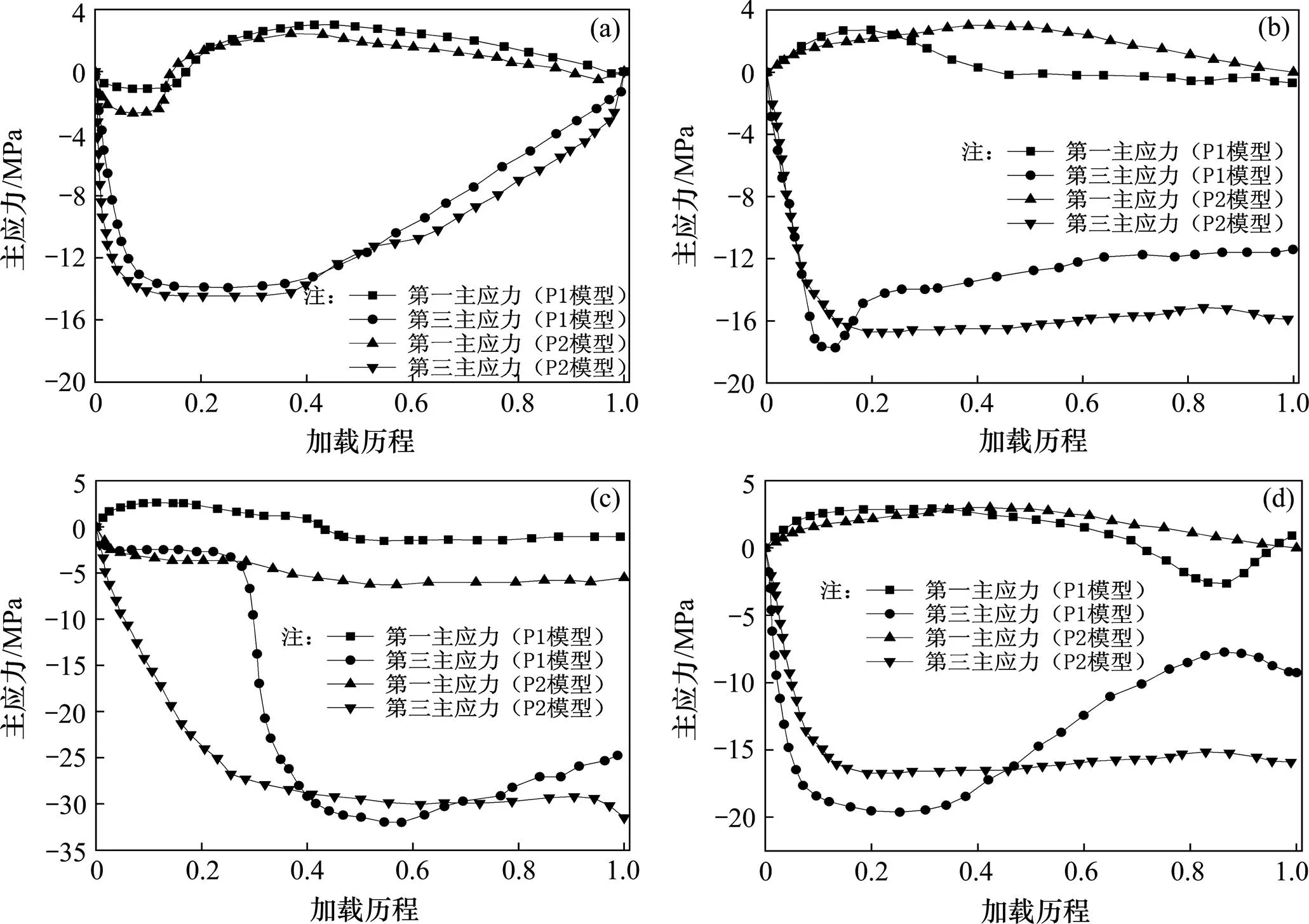
在加载末期，标准试件与埋入式试件中混凝土块的应力云图见图5，由图5可知，在标准试件中，混凝土块在靠近开孔板附近区域，混凝土的拉应力较大，已超过其抗拉强度2.64 MPa，出现开裂现象；在埋入式试件中，混凝土块仅在开孔板孔口附近区域拉应力水平较大，其他区域拉应力水平较低，且均未超过混凝土的抗拉强度2.64 MPa。由于混凝土榫在与开孔板接触的局部区域的受力情况较为复杂，分别提取混凝土榫上、下、左、右侧单元的主应力加载历程结果分析其受力状态；图6为混凝土榫四周区域典型单元的主应力图，图中加载总历程为单位1。由图6可知，在2类试件中，混凝土榫上侧单元的拉应力变化较为一致，在加载初期均处于三向受压状态。混凝土榫下侧单元在埋入式试件中始终处于三向受压状态，原因是此区域混凝土受到孔洞和贯通钢筋挤压而侧向约束较弱所致。混凝土榫的左、右侧单元在2类试件中的破坏均始于混凝土开裂，在标准试件中，由于偏心加载力的作用，混凝土榫左侧应力水平明显高于右侧，而在受纯剪作用的埋入式试件中，混凝土榫左右侧应力水平几乎相同。

试验结果中，ST16试件在加载时首先在开孔板外侧的混凝土出现裂纹，裂缝逐渐扩展形成包围剪力键的裂缝，最终导致PBL失去约束，试件由于混凝土块失效而破坏；PT16试件的混凝土板除与PBL接触的部分区域，大部分仍处于完好状态。

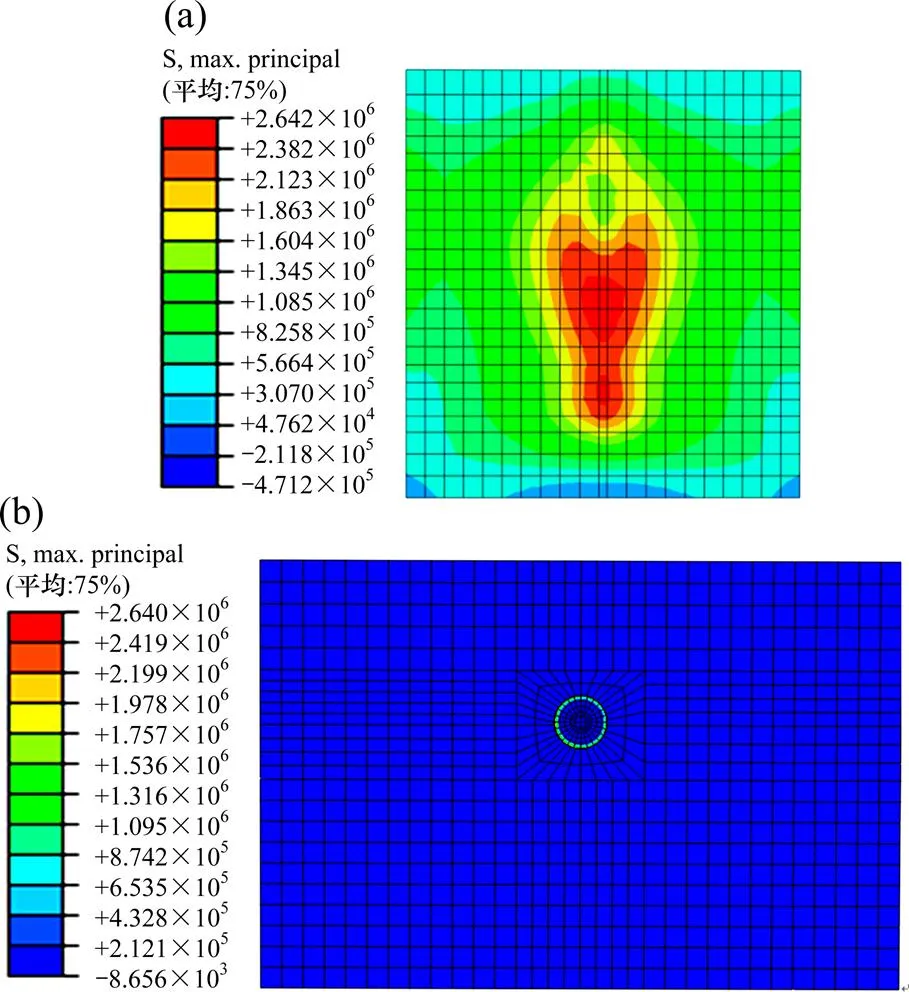
单位：Pa

2.3.2 钢梁与贯通钢筋

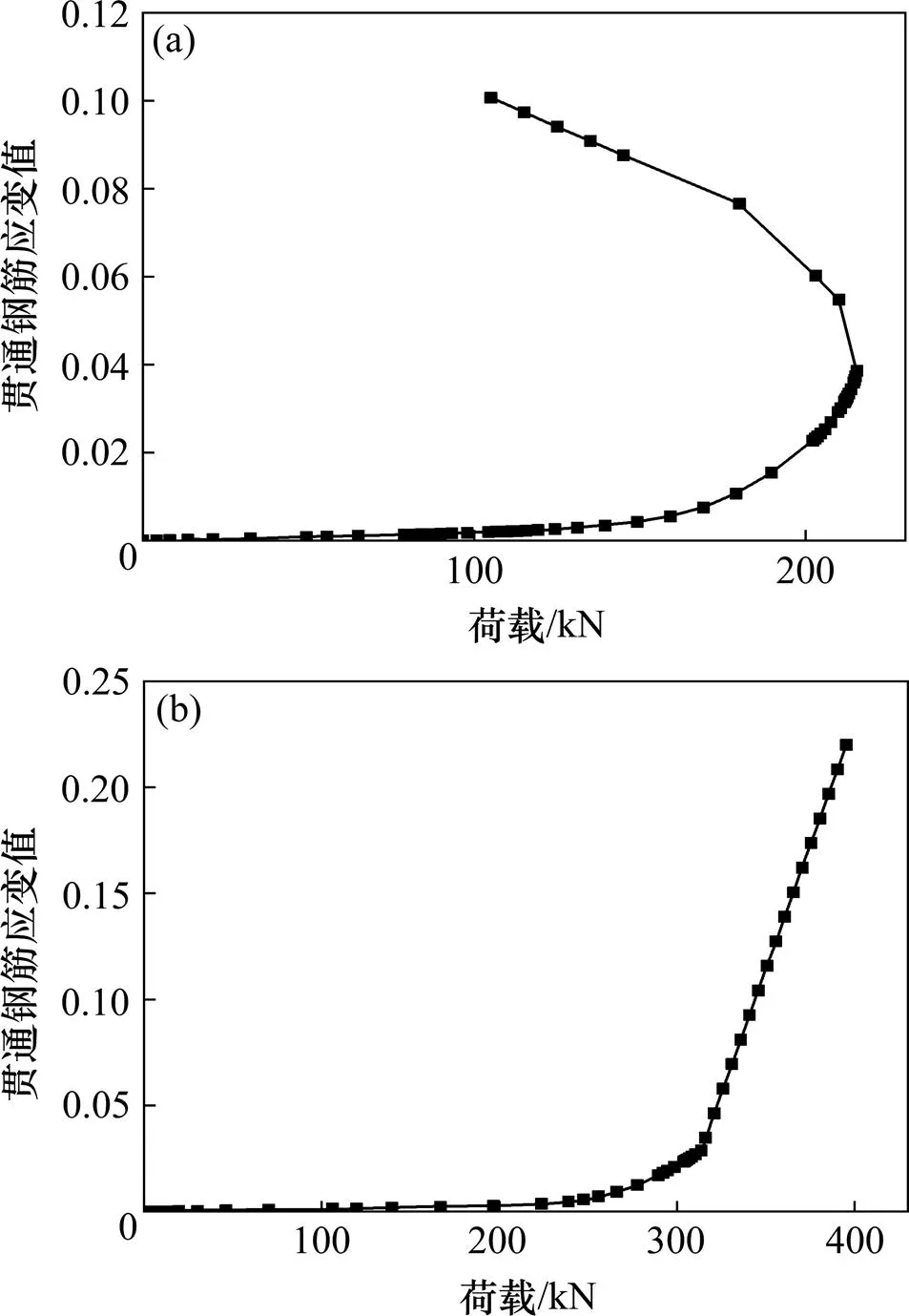
标准试件在加载末期，开孔板的变形图及贯通钢筋的荷载−应变曲线分别见图7(a)和图8(a)；由图可知，在标准试件中，开孔板在破坏时较为完好，由于加载端偏心效应，开孔板外侧变形明显大于内侧。贯通钢筋在加载初期处于弹性阶段，随着荷载增大，贯通钢筋的应变值迅速增加，但直至试件破坏贯通钢筋仍未达到其极限应变。埋入式试件在加载末期，开孔板变形图如图7(b)所示，从图可知，开孔板孔口上侧变形较大，左右两侧变形量较小且对称；在试件破坏时，贯通钢筋达到其极限应变。

单位：MPa

单位：m

(a) P1模型贯通钢筋荷载−应变曲线；(b) P2模型贯通钢筋荷载−应变曲线

试验结果中，ST16试件破坏时开孔板与贯通钢筋变形较小；而PT16试件在加载末期贯通钢筋被剪断，开孔钢板发生向加载端一侧的凹陷变形。综合对比计算与试验结果可知，两者的破坏特征符合得较好。由此可见，PBL标准试件的破坏始于混凝土开裂，最终由于开孔板附近的混凝土产生较大裂缝而导致试件破坏，破坏时贯通钢筋的变形量较小；PBL埋入式试件的破坏是由于贯通钢筋被剪断，此时开孔板向加载端方向产生较大凹陷，破坏时混凝土除与孔口接触的局部区域开裂外，大部分的混凝土仍然完好。

2.4 2类推出试验的破坏机理

通过以上对比分析可见：标准试件是由于混凝土裂缝较大而不能对PBL形成有效约束而破坏；埋入式试件则是由于贯通钢筋在剪−拉联合作用下发生较大的塑性变形，最终达到其极限抗拉强度而引起的破坏，2类推出试验的破坏机理迥异。

破坏机理的不同则导致了2种试验构造下PBL抗剪性能的差异，标准试件的破坏源于混凝土块开裂，而贯通钢筋在试件破坏前并未破坏，因此在标准推出试验中，PBL抗剪性能的上限取决于混凝土；在埋入式试件中，加载力垂直作用与开孔板，PBL接近与纯剪的受力状态；此外，混凝土块较厚且剪力键埋入较深，混凝土局部高应力状态可以通过应力重分布得到相当程度的释放；贯通钢筋随着荷载的不断增大最终由于剪−拉联合作用而破坏。由于贯通钢筋的极限强度和变形性能都远优于混凝土，因此PBL在埋入式试验中的极限承载力高于标准推出试验。

3 PBL极限承载力主要影响因素

由以上对比分析可知，由不同构造推出试验得到的PBL极限承载力差异较大；此外，由于PBL的主要受力构件为混凝土榫及贯通钢筋，且混凝土强度、开孔板孔径、贯通钢筋直径对PBL极限承载力有重要影响[5, 7]，为此，进一步研究在2类推出试验中，以上3种因素对PBL极限承载力的影响，开展PBL极限承载力的单因素变量参数分析。

3.1 混凝土强度

分别采用C30，C40和C50等级混凝土对2类试件进行计算，其荷载−滑移曲线如图9所示，从图中可以看出，混凝土强度对PBL的荷载−滑移曲线有较大影响，主要表现为：在标准推出试验中，采用C30，C40和C50等级的混凝土时，PBL的极限承载力分别为167.3，194.6和214.8 kN，相较于C30混凝土，采用C40和C50混凝土的PBL试件极限承载力分别增加了16.3%和28.4%；

在埋入式试验中采用C30，C40和C50等级的混凝土时，PBL的极限承载力分别为308.9，342.5和375.4 kN，相较于C30混凝土，采用C40和C50混凝土的PBL试件极限承载力分别增加10.9%和21.5%。相较于埋入式试验，在标准推出试验中，PBL的极限承载力受混凝土强度的影响更大。

3.2 开孔板孔径

分别采用开孔板孔径为c=40，50和60 mm的2类试件进行计算，其荷载−滑移曲线如图10所示，从图中可以看出，在标准推出试验中，采用c=40，50和60 mm的开孔板孔径时，PBL的极限承载力分别为162.0，187.0和214.8 kN，相较于c=40 mm的试件，采用c=50 mm和60 mm的PBL极限承载力分别增加了15.4%和32.6%；

而在埋入式试验中采用c=40，50和60 mm的开孔板孔径时，PBL的极限承载力分别为287.6，331.7和375.4 kN，相较于c=40 mm的试件，采用c=50 mm和60 mm的PBL极限承载力分别增加15.3%和30.4%。在2类推出试验中，开孔板孔径对PBL极限承载力均有较大影响且影响程度相当。

(a) 标准推出试验；(b) 埋入式试验

(a) 标准推出试验；(b) 埋入式试验

3.3 贯通钢筋直径

分别采用贯通钢筋直径为s=16，20和24 mm的2类试件进行计算，其荷载−滑移曲线如图11所示，从图中可以看出，在标准推出试验中，随着贯通钢筋直径的增大，PBL极限承载力增幅很小；在埋入式试验中采用s=16，20和24mm的贯通钢筋直径时，PBL的极限承载力分别为375.4，430.8和530.2 kN，相较于s=16 mm的试件，采用s=20 mm和24 mm的PBL极限承载力分别增加14.7%和41.2%；相较于标准推出试验，在埋入式试验中，贯通钢筋直径是PBL极限承载力的重要影响因素。此种现象与2类试件的破坏机理密切相关：标准试件的破坏始于混凝土开裂，PBL的极限承载力很大程度上由混凝土强度及混凝土榫直径控制；埋入式试件的破坏由贯通钢筋控制，因此在埋入式试验中PBL的极限承载力受贯通钢筋的影响较大。

(a) 标准推出试验；(b) 埋入式试验

4 结论

1) 提供一种有效的方法模拟PBL剪力键的推出试验，非线性有限元方法得到的PBL荷载−滑移曲线、抗剪性能指标、构件的破坏形态与试验结果吻合较好。

2) 在标准与埋入式2种推出试验中，相同参数的PBL剪力键的抗剪性能差异较大，主要表现为承载力与滑移性能的不同。相较于标准推出试验，在埋入式试验中，PBL剪力键的极限承载力约为前者的1.8倍左右，滑移量为前者的2倍左右。

3) PBL标准试件与埋入式试件的破坏机理迥异，前者的破坏是由于开孔板附近的混凝土裂缝过大、混凝土不能有效约束剪力键所致；后者的破坏源于贯通钢筋在剪−拉联合作用下被剪断。

4) 在埋入式试验中，混凝土强度、开孔板孔径与贯通钢筋直径对PBL的极限承载力均有较大影响；而在标准推出试验中，贯通钢筋直径对PBL极限承载力的影响较小，混凝土强度、开孔板孔径的影响则较大。

[1] Kim S H, Lee C G, Ahn J H, et al. Experimental study on joint of spliced steel–PSC hybrid girder, Part I: Proposed parallel-perfobond-rib-type joint[J]. Engineering Structures, 2011, 33(8): 2382−2397.

[2] Valente I, Cruz P J S. Experimental analysis of perfobond shear connection between steel and lightweight concrete[J]. Journal of Constructional Steel Research, 2004, 60(3−5): 465−479.

[3] Kim H Y, Jeong Y J. Experimental investigation on behaviour of steel–concrete composite bridge decks with perfobond ribs[J]. Journal of Constructional Steel Research, 2006, 62(5): 463−471.

[4] Vianna J D C, Costa-Neves L F S, Vellasco P C G D, et al. Experimental assessment of perfobond and T- perfobond shear connectors’ structural response[J]. Journal of Constructional Steel Research, 2009, 65(2): 408−421.

[5] 曹学亮, 李法雄, 雷俊卿, 等. 基于ABAQUS的开孔板连接件抗剪承载力分析[J]. 公路交通科技, 2013, 30(11): 89−95. CAO Xueliang, LI Faxiong, LEI Junqing, et al. Analysis of shear-capacity of perfobond shear connectors based on ABAQUS software[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 89−95.

[6] 张清华, 李乔, 卜一之. PBL剪力连接件群传力机理研究Ⅱ:极限承载力[J]. 土木工程学报, 2011, 44(5): 101−108. ZHANG Qinghua, LI Qiao, BU Yizhi. Load transmission mechanism of PBL shear connector groups Ⅱ: load capacity[J]. China Civil Engineering Journal, 2011, 44(5): 101−108.

[7] 胡建华, 叶梅新, 黄琼. PBL剪力连接件承载力试验[J].中国公路学报, 2006, 19(6): 65−72. HU Jianhua, YE Meixin, HUANG Qiong. Experiment on bearing capacity of PBL shear connectors[J]. China Journal of Highway and Transport, 2006, 19(6): 65−72.

[8] 肖林, 卫星, 强士中. 两类PBL剪力键推出试验的对比研究[J]. 土木工程学报, 2013, 46(11): 70−80. XIAO Lin, WEI Xing, QIANG Shizhong. Comparative study on two kinds of push-out tests of PBL shear connectors[J]. China Civil Engineering Journal, 2013, 46(11): 70−80.

[9] 石宵爽, 王清远, 欧阳雯欣, 等. PBL剪力连接件粘结滑移性能的静载推出试验研究[J]. 工程力学, 2012, 29(1): 168−175. SHI Xiaoshuang, WANG Qingyuan, OUYANG Wenxin, et al. Push-out experimental study on bond-slip behaviors of PBL shear connector under static loading[J]. Engineering Mechanics, 2012, 29(1): 168−175.

[10] 汪维安, 李乔, 赵灿晖, 等. 混合结构PBL剪力键群承载力试验研究[J]. 土木工程学报, 2014, 47(6): 109−117. WANG Weian, LI Qiao, ZHAO Canhui, et al. Experimental study on bearing capacity of PBL shear connector group in hybrid structures[J]. China Civil Engineering Journal, 2014, 47(6): 109−117.

[11] 张勇. 南京长江第三大桥桥塔钢混结合段结构特性研究[D]. 成都: 西南交通大学, 2005. ZHANG Yong. Research on the structural characteristics of steel-concrete composite segment in the tower of Nanjing Yangtse 3RD bridge[D]. Chengdu: Southwest Jiaotong University, 2005.

[12] 王振海. 埋入式PBL剪力连接件力学特性及承载机理研究[D]. 成都: 西南交通大学, 2012. WANG Zhenhai. Study on mechanical property and load-bearing mechanism of embeded perforbond rib shear connectors[D]. Chengdu: Southwest Jiaotong University, 2012.

[13] 张清华, 李乔, 唐亮. 桥塔钢−混凝土结合段剪力键破坏机理及极限承载力[J]. 中国公路学报, 2007, 20(1): 85− 90. ZHANG Qinghua, LI Qiao, TANG Liang. Fracture mechanism and ultimate carrying capacity of shear connectors applied for steel-concrete joint segment of bridge pylon[J]. China Journal of Highway and Transport, 2007, 20(1): 85−90.

[14] 庞芝炯, 周志祥. 基于塑性损伤模型的PBL推出试件数值分析方法[J]. 中外公路, 2014, 34(5): 110−114. PANG Zhijiong, ZHOU Zhixiang. Numerical analysis method for PBL push out specimen based on plastic damage model[J]. Journal of China & Foreign Highway, 2014, 34(5): 110−114.

[15] 刘巍, 徐明, 陈忠范. ABAQUS 混凝土损伤塑性模型参数标定及验证[J]. 工业建筑, 2014, 8(增1): 227. LIU Wei, XU Ming, CHEN Zhongfan. Parameter calibration and verification of ABAQUS damage plasticity model for concrete[J]. Industrial Construction, 2014, 8(Suppl 1): 227.

[16] 苏庆田, 杜霄, 李晨翔, 等. 钢与混凝土界面的基本物理参数测试[J]. 同济大学学报(自然科学版), 2016, 44(4): 499−506. SU Qingtian, DU Xiao, LI Chenxiang, et al. Tests of basic physical parameters of steel-concrete interface[J]. Journal of Tongji University (Natural Science), 2016, 44(4): 499−506.

[17] 王振海, 赵灿晖, 李乔. PBL剪力键荷载-滑移关系试验研究[J]. 西南交通大学学报, 2011, 46(4): 547−552. WANG Zhenhai, ZHAO Canhui, LI Qiao. Experimental investigation on load-slip relationship of perfobond rib shear connectors[J]. Journal of Southwest Jiaotong University, 2011, 46(4): 547−552.

Study on the failure mechanism and bearing capacity influence factors of two kinds of push-out tests of PBL

SHI Zhou, QIN Bocong

(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

In order to explore the failure mechanism and the main influencing factors of the ultimate bearing capacity of the two types of push-out test of PBL, the fine finite element model of the two kinds of PBL push-out tests was established by using the nonlinear finite element method based on the Abaqus platform. The calculation results show that the ultimate bearing capacity and slip performance of PBL in the embedded push-out test is better than that of the standard push-out test, and the nonlinear finite element calculation results are in good agreement with the test results. In two types of push-out test of PBL, the failure mechanism and the failure form of the main components are different. The failure of the specimen in the standard push-out test is due to the cracking of the concrete, while that in the embedded test is due to the failure of the perforated rebar. The parameter analysis shows that the ultimate bearing capacity of PBL is mainly related to the strength of concrete and the aperture of perforated plate in the standard push-out test. In the embedded test, the strength of concrete, the aperture of the perforated plate and the diameter of the perforated rebar have great influence on the ultimate bearing capacity of the PBL.

PBL shear connector; push-out test; Abaqus; failure mechanism; parameter analysis

10.19713/j.cnki.43−1423/u.2019.04.015

TU398

A

1672 − 7029(2019)04 − 0943 − 10

2018−05−09

中国铁路总公司科技开发计划重大项目(2017G006-A)

施洲(1979−)，男，江苏滨海人，副教授，博士，从事桥梁结构试验及性能评定研究；E−mail：zshi1979@swjtu.cn

(编辑 涂鹏)