基于多目标优化的含电力电容器的农网系统调度策略研究
2019-04-26刘冰冰周文俊
刘冰冰,周文俊
(温州商学院 信息工程学院,温州 325000)
0 引言
农网是电网系统的重要组成部分,农网系统调度的目的是在保证电网安全可靠运行的条件下,最大限度地提高农网运行的经济性和可靠性。研究含电力电容器的农网系统调度可以有效改善电能质量、降低农网系统的网损,提高农网系统的安全性[1]。本文在传统农网调度研究的基础上,针对含风电系统的农网电力系统,将柔性负荷引入农网调度系统,提出一种基于多目标优化的含电力电容器的农网系统调度策略研究方法。
1 灰狼优化算法
GWO算法[2](Grey Wolf Optimization Algorithm,GWO)是受灰狼捕食行为启发而提出的仿生寻优算法[3],该算法将灰狼群体按照金字塔等级原则分为α、β、δ、ω4个等级,等级分层如图1所示。
其中,α表示头狼,在狼群群体中处于最高等级,主要进行灰狼群体内部事务的决策和调度;β是α的智囊团队,起到参谋的作用,协助头狼管理狼群内部事务;δ受α和β指挥和领导,在灰狼群体中主要进行侦查、放哨、捕猎以及幼狼的看护事务;ω处于金字塔的最底层,主要负责平衡狼群内部关系和看护幼狼事务。在GWO算法中,狼群种群位置的更新如式(1)、式(2)[6]:
图1 灰狼种群等级图
D=|C·Xp(t)-X(t)|
(1)
X(t+1)=Xp(t)-A·D
(2)
式中,A=2a·r1-a,C=2·r2,Xp表示猎物的位置,X表示灰狼的位置,t表示当前迭代次数,随着寻优过程的进行,a由2线性下降到0,r1,r2表示为[0,1]的随机向量。
假设α、β、δ为猎物最可能处于的位置,在GWO算法中,将前3个变量的最优解分别赋值给α、β、δ,而其他灰狼被当作为ω,其可以根据α、β、δ的位置实现重新定位。狼群ω的位置调整如式(3)-式(5)[4-5]:
Dα=|C1·Xα-X|
(3)
Dβ=|C2·Xβ-X|
(4)
Dδ=|C3·Xδ-X|
(5)
式中,Xα、Xβ、Xδ分别表示α、β、δ的位置,C1、C2、C3分别表示随机数,X为当前解的位置。在公式(3)-公式(5)的基础上,分别计算当前解和α、β、δ之间的近似距离,在此基础上,当前解的最终位置如式(6)-式(9)[6]:
X1=Xα-A1·(Dα)
(6)
X2=Xβ-A2·(Dβ)
(7)
X3=Xδ-A3·(Dδ)
(8)

(9)
式中,Xα、Xβ、Xδ分别为α、β、δ的位置,A1、A2、A3为随机数,t为当前迭代次数。
2 含电力电容器的农网系统多目标优化调度模型
2.1 含电力电容器的风电农网系统模型
含电力电容器的风电农网系统由光伏列阵、柴油发电机、微型燃气轮机、燃料电池、储能装置、风机、逆变器等分布式电源及其控制器构成[6-7],之后,农网系统通过公共连接点和配电网连接起来,其模型图如图2所示。
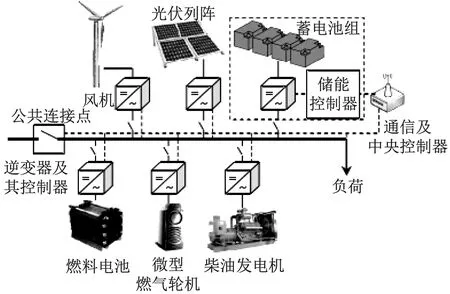
图2 含电力电容器的风电农网系统模型
2.2 目标函数
(1)农网系统运行成本最小
①农网系统的发电成本
火电机组发电成本数学模型为[8]式(10)。
(10)
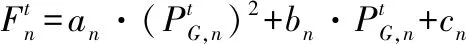
②可中断负荷补偿成本如式(11)。
(11)

③激励负荷成本如式(12)。
(12)

农网系统发电成本的最小化数学模型可描述为式(13)。
(13)
(2)污染气体排放量最小
本文考虑CO2、NOx、SO2三种气体的影响如式(14)。
kNOx·ENOx+kSO2·ESO2)
(14)
其中,Me表示总污染气体排放量,Cln表示煤耗量系数,kNOx、kSO2表示NOx、SO2相对于CO2的污染严重系数,ECO2、ENOx、ESO2分别表示单位煤耗量所对应的CO2、NOx、SO2排放量。
(3)农网系统运行风险最小
本文定义系统的运行风险程度如式(15)-式(19)。
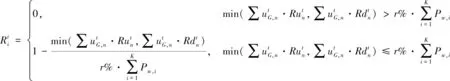
(15)
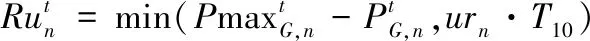
(16)
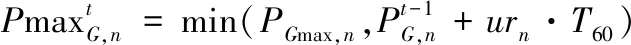
(17)
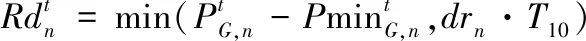
(18)
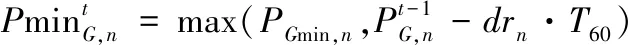
(19)
2.3 约束条件
(1)功率平衡约束如式(20)。
(20)

(2)各单元出力上下限约束如式(21)。
(21)
(3)旋转备用容量约束
正旋转备用如式(22)、式(23)。
(22)
负旋转备用:
(23)
其中,L%表示用电负荷对备用需求系数;us%、ds%分别表示风电对正备用需求系数和负备用需求系数。
(4)机组爬坡速率约束如式(24)。
船舶电力系统故障一般有局部配电板故障、发电机故障、推进器失效故障、全船失电故障等。本文以工况3(较恶劣海况,发电机组无/有隐藏故障两种情况)条件下,主汇流排发生短路故障为例,仿真分析系统动态响应,对电力系统设计进行验证。在仿真模型中,电力系统故障响应动作的要求和保护开关动作顺序的要求均按DP-ER附加标志要求进行设置,同时发电机均设置为热备机状态,以降低备用冗余发电机并入电网时对电网的冲击。
(24)
(5)机组最小起停时间约束如式(25)。
(25)

(6)可中断负荷中断时间约束如式(26)。
(26)
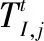
(7)可中断负荷中断次数约束如式(27)。
(27)
其中,Nj表示在整个周期内第j个可中断负荷用户所允许的负荷中断的最大次数。
3 基于GWO的农网系统调度策略优化研究
GWO算法求解农网系统调度策略优化过程如下所示,其流程框图如图3所示。
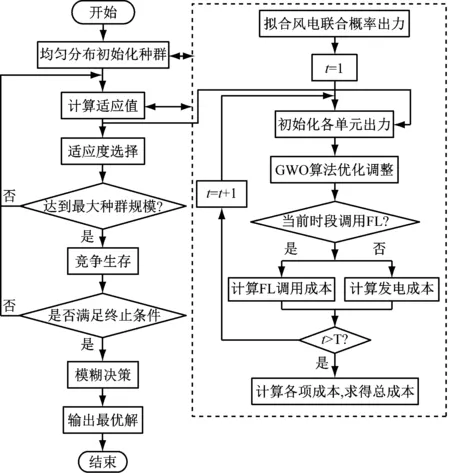
图3 基于GWO算法的农网系统调度策略优化
Step1:输入电网相关信息,如风电场规模、负荷要求和中断时间等要求;
Step2:根据优化变量的取值范围,随机生成初始化种群;
Step3:计算每个灰狼的适应度函数值;
Step4:对适应度进行排序,将适应度排名前三的灰狼定义和保存为Xa、Xb、X;
Step5:调整和更新狼群ω的位置;
Step6:更新参数a、A、C;
Step7:若gen>maxgen,保存最优解;否则,gen=gen+1,返回Step4,重新寻优。
4 实证分析
4.1 数据来源
为了验证GWO算法进行含电力电容器的农网系统调度策略的优越性,选择文献中的模型和参数为研究对象,该模型含电力电容器和风电接入,共有10台常规风机,其中包括功率规模分别为150 MW和100 MW的2个并网风电场。模型相关参数设定如下:调度时段数T=24(每时段1小时),风电波动备用系数r%=20%,可中断负荷最大、最小中断时间分别为6 h、2 h,最大中断次数为Nj均为3 h,负荷对备用的需求系数L%=7%,风电对正、负备用需求系数us%取值范围为[10%20%],ds%的取值范围为[10%30%],柔性负荷参数如表1所示。
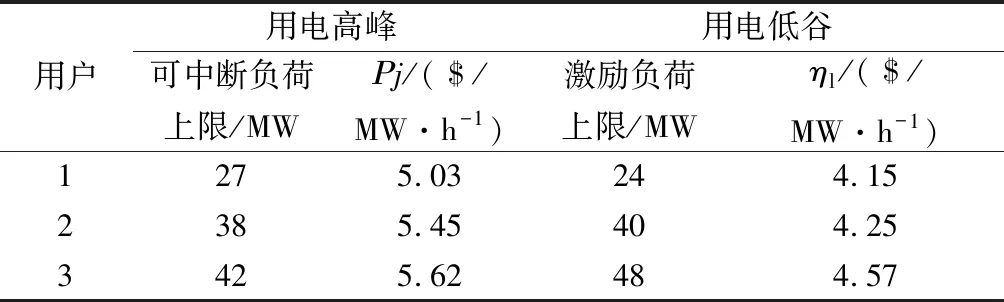
表1 柔性负荷参数
4.2 结果分析
4.2.1 考虑风电输出相关性和柔性负荷的多目标供需互动调度策略
设定GWO算法的最大迭代次数为100,种群规模为50,运用GWO算法求解可得负荷和各单元出力情况如图4所示。
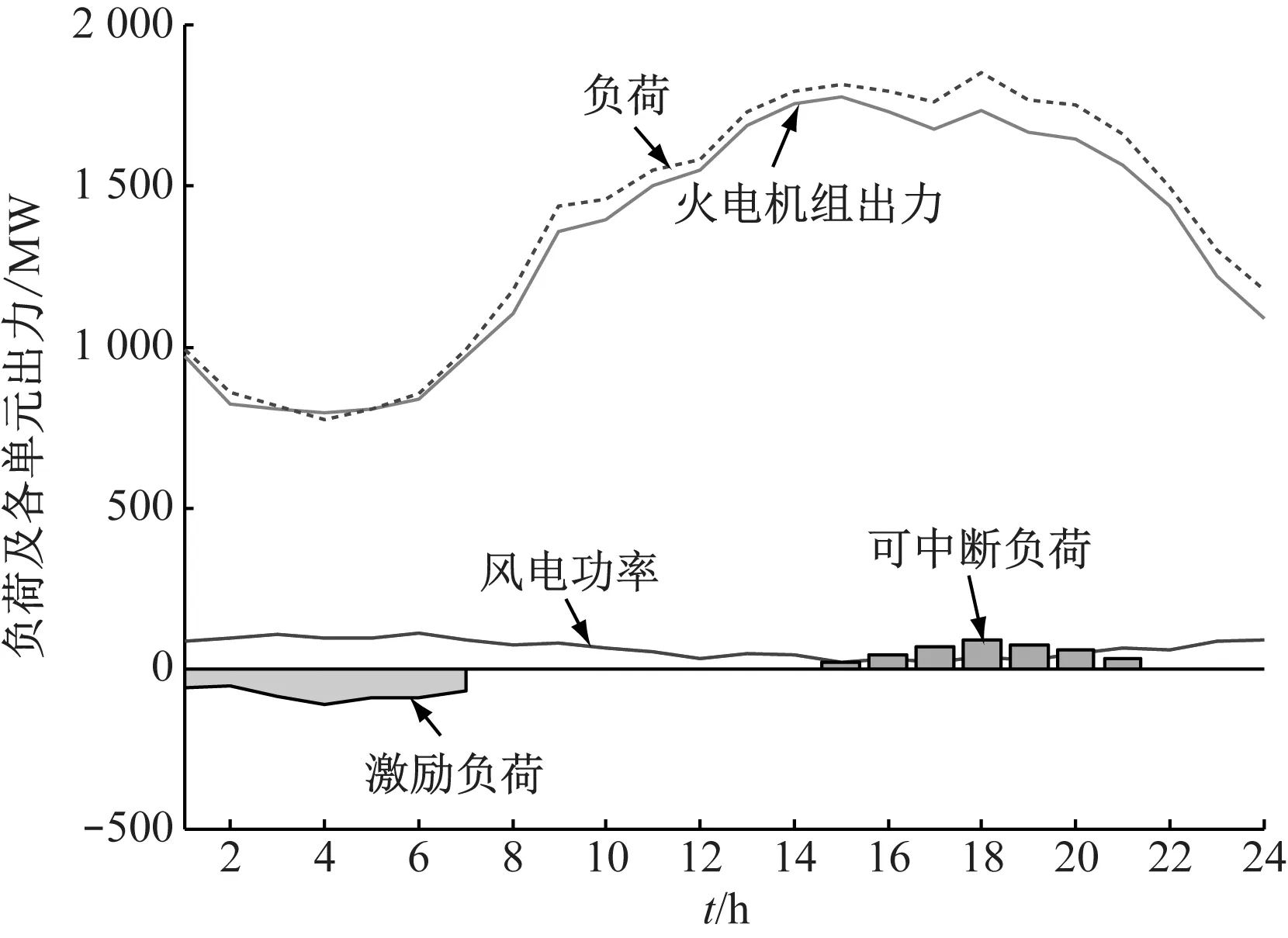
图4 负荷及各单元出力情况
4.2.2 调度策略对比
为了对比各因素对农网系统调度结果的影响,在考虑了风电出力结构和柔性负荷两个因素的基础上,本文对如下3种方案进行验证,3种方案如下:
方案1:仅考虑农网系统中的风电出力结构的调度方案;
方案2:仅考虑农网系统中的柔性负荷调节的调度方案;
方案3:综合考虑风电出力结构和柔性负荷调节的调度方案;
3种调度方案求解的的经济和环境效益结果如表2所示。

表2 3种方案的经济和环境效益
由表2可知,方案2比方案1多考虑了柔性负荷因素,总运行成本降低了1.19%,污染气体排放量降低了1.12%,发电成本、总运行成本以及污染气体排放量均有了一定程度降低。
方案3比方案2多考虑了风电场出力结构因素,总运行成本降低了1.23%,污染气体排放量降低了1.04%。综合结果,考虑风电出力结构和柔性负荷调峰的调度方案在环境效益和经济效益上较单一方案1或者方案2具有更明显的优势。
4.2.3 不同算法结果对比
为了说明GWO算法的优越性,将GWO和遗传算法[12](Genetic Algorithm,GA)、粒子群算法(Particle Swarm Optimization Algorithm,PSO)、果蝇优化算法(Fruit Flying Optimization Algorithm,FOA)优化结果对比结果如表3所示。

表3 不同算法结果
由表3可知,本文算法GWO结果优于FOA、PSO和GA算法,总运行成本、污染气体排放量的目标函数值更小,表明GWO算法具有更好的收敛特性。如图5所示。
由图5可知,本文算法GWO具有更快的收敛速度,效果优于FOA、PSO和GA算法,长期看来,可以节省更多成本,降低污染物的排放。
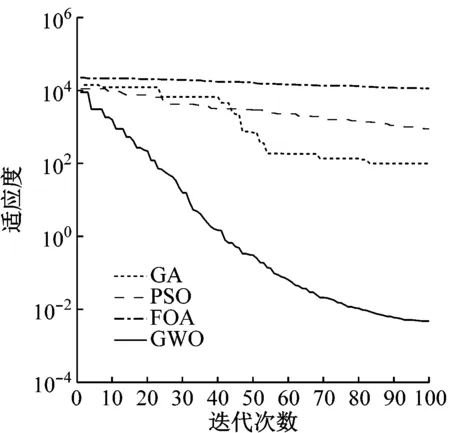
(a)方案1
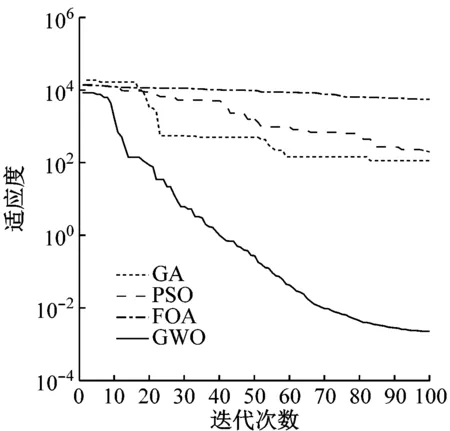
(b)方案2

(c)方案3
图5 寻优收敛图
5 总结
针对含风电系统的农网电力系统,将柔性负荷引入农网调度系统,提出一种基于多目标优化的含电力电容器的农网系统调度策略研究方法。研究结果表明,与FOA、PSO和GA算法相比,GWO算法具有更快的收敛速度,总运行成本、污染气体排放量的目标函数值更优。
