优化贝叶斯的数据融合算法
2019-04-26宋蕾
文/宋蕾
1 绪论
无线传感器技术被广泛应用于现代测量仪器与系统中,多个节点采集的数据通过数据融合技术,能够得到更为精确与可靠的估计信息,相比于单一传感器的测量系统能够明显改善系统的精度与可靠度。针对于数据的准确性问题,苘大鹏等人提出了E-CPDA 算法,陈羽中等提出了基于多人博弈的融合算法(MGDAA 算法),崔艳玲等提出的基于车辆检测器数据的压缩重构以及融入交通流特征的Megrez 融合算法。通过研究分析上述三种算法,本文提出了一种优化贝叶斯的数据融合算法,针对于多个同质传感器对同一被测量的数据进行研究与分析,通过实例分析,从数据的准确性角度来验证本文算法的可靠性。
2 网络模型
传感网中包含有N 个节点M 个簇结构,针对于网络模型所做的假设如下:
(1)网络内的节点同构并且为之固定,每个节点具有自己的ID 号码并且唯一;
(2)簇首节点能够感知簇内节点的剩余能量大小,每个簇内节点可以感知到自己的剩余能量大小;
(3)不论网络内节点剩余能量大小多少,消耗的能量总是小于节点的剩余能量。
3 改进贝叶斯的数据融合算法
3.1 置信距离理论
传感器节点所采集的数据在融合之前,需要对每个数据进行有效性判断,由于被测量参数来自同质传感器,因此采用置信距离理论,依据数据的统计特性完成有效性与可靠性的判断。假设节点采集的数据服从正太分布,令xi(i=1,2,3,...,j,...n)表示第i 个节点所采集与输出的数据,pi(x)表示xi的概率密度函数,那么第i 个节点与第j 个节点之间的置信距离公式如下:

dij表示xi对xj的置信距离,dji表示xj对xi的置信距离,由于xj与xi均服从正太分布,可以得知,当xi=xj的时候,dij=dji=0 总是成立;当xi>>xj或者xi< 由上述公式能够得到n 个节点中任意两个输出数据之间的置信。因为置信距离反映了节点输出数据之间的相互支持关系,因此定义二值关系矩阵来说明两个输出数据之间的关联关系。令rij 表示第i 个节点对第j 个节点的支持关系,其中1 表示支持,0 表示不支持,并且令αij为阈值,依据实际的节点测量信息进行计算与分析,公式如下: 依据二值关系判断任意两个节点之间的支持关系,m 表示临界值,当多于m 个节点输出支持数据时则认为输出数据有效,进而得到l 个有效数据,以完成数据的融合处理。 简化的贝叶斯估计公式表示后验概率p(x|y)等于似然函数p(y|x)乘以先验公式p(x)除以归一化公式,可以理解为对先验知识的动态优化。通过置信距离能够得到l 个有效数据,表示(x1,x2,..,xl),被测量参数的条件概率公式如下: 通过仿真实验的数据可知,DAAGT 算法、E-CPDA 算法、MGDAA 算法与Megrez 算法的融合结果准确性随着传感器节点个数的增多,均有所上升,但是DAAGT 算法的上升幅度最大且数据准确性高于其他三个算法,数据准确性分别提高了0.041、0.212 和0.105。
3.2 贝叶斯估计公式
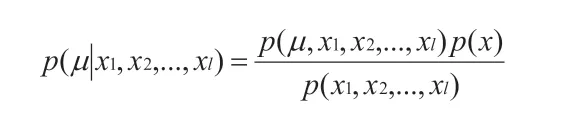
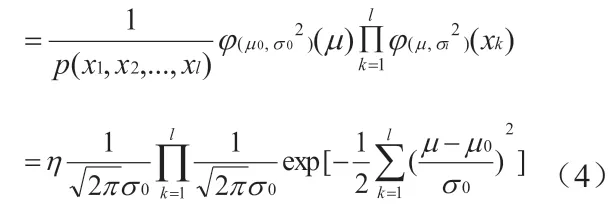
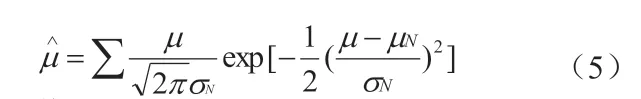
4 仿真分析
