基于直方图峰值优化的阶梯k-means 聚类算法

文/李芝峰 景源

1 引言

K-means 是无监督学习中最为常用的经典算法，也是数据挖掘算法中很经典的算法之一。K-means 算法和初始聚类中心点的选择有很大的关系，合理的初始聚类中心点不仅能够增加分类的准确率，而且还能够减少迭代次数，缩短运算时间。传统的K-means 算法原理简单，但是有一下几个四个缺陷：

（1）传统算法对于噪音点敏感，对异常点不稳定，而且传统算法比较容易陷入局部最优解中，得到的结果和我们理想的结果有些差距。

（2）初始聚类中心是随机选择，每次都会选择不同的初始聚类中心，算法的计算效率时好时坏。

（3）只能发现球状簇规则的分布。

（4）K-means 算法是属于无监督学习算法的一种，K 值需要根据研究人员的经验事先指定，在多种类别混合的数据中，不能够很好的确定分类K 值。

K-means 聚类算法可以应用在不同的领域，文献[3]对K-means 算法改进并应用在音频处理中。该算法适合应用在音频分离上，阶梯K-means 算法对多维数据进行降维处理，通过直方图分布能够得到数据的峰值区间，也就是高密度分布区域，初始聚类中心点大多都属于这个峰值区间，从这个峰值区间选取的初始聚类中心点很接近聚类的中心区域，很显然通过峰值得到的K 个初始聚类中心点能够很大程度上减少计算量。

2 常用K-means算法介绍

2.1 传统K-means算法

传统K-means 算法是一个无监督学习，它把数据分成若干类，统一类中的数据相似性应可能的大，不同类中的数据的差异性应尽可能的大。传统K-means 算法是在人工指定K值的情况下，随机选择K 个点作为初始聚类中心。

传统K-means 算法的步骤分为：

（1）随机选取K 个点，作为K 类的初始聚类中心点，记做C={c1, c2…ck,}

（2）遍历所有的数据点vj，计算欧式距离，找到距离C={c1,c2…ck,}最近的聚类并加入

（3）分别计算K 类所有数据的中心点，作为该类新的聚类中心

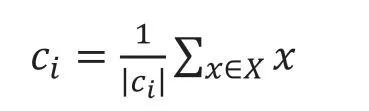
（4）重复进行（2）（3）步骤，直到每一类的聚类中心不再发生变化

传统K-means 聚类算法是基于局部最优

2.2 K-means++算法

K-means++算法主要改善了传统K-means算法初始聚类中心点选择，对初始聚类中心的选择比较符合人类的直觉：中心点之间的距离越远越好。

K-means++算法的具体步骤为：

（1）随机选取一个点，作为初始聚类中心点，记做c1；

（2）遍历所有的数据点vj，找到距离已有聚类中心C={c1,c2…ck,}之间最近距离，用D(x)表示；

（4）重复进行（2）（3）步骤，直到选出K 个聚类中心C={c1,c2…ck,}

K-means++聚类算法还是随机第一个初始聚类中心点，花费了额外的时间来计算初始聚类中心点，但是减少了迭代的次数，本身能够快速的收敛。

3 直方图峰值优化的K-means算法

从密度集中区域选择的点作为初始中心点，可以很好的区分各个聚类集合，并能够减少一定的计算迭代次数。在统计数据的时候，按照频数的分布表，在二维坐标体系中，横坐标代表每组的端点，纵坐标代表频数，这样的统计图叫做频数分布直方图。先对N 维数据XN(1,2,…n)进行初步的处理，将多维数据XN(1,2,…n)降维成一维数据Xi（i=1……j）并排序，这样我们能够得到开始点Xs和结束点Xe，求的这两个点之间的距离dx=Xe-Xs，文献[4]默认分组的数量为s=3*K，每一组的距离是d=dx/s。

改进后算法的步骤：

（1）对全体数据集XN 进行维度拆分，拆分成一维数据集Xi（i=1……j），默认分组数量为常数s

（2）取一维数据集作为X1i（i=1……m）进行排序，得到Xs和Xe，并计算得到dx

（3）根据步骤2，得到组间距d，生成分组为s 的直方图H1，得到直方图H1峰值Fi1，把峰值后的数据作为新的数据集X2i（i=1……n），重新生成分组为s 的直方图H2，得到直方图H2峰值Fi2，以此类推得到K 个峰值

表1：三种数据的聚类性能比较

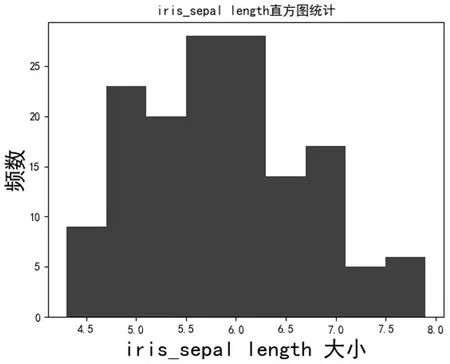
图1：iris_sepal length 直方图统计

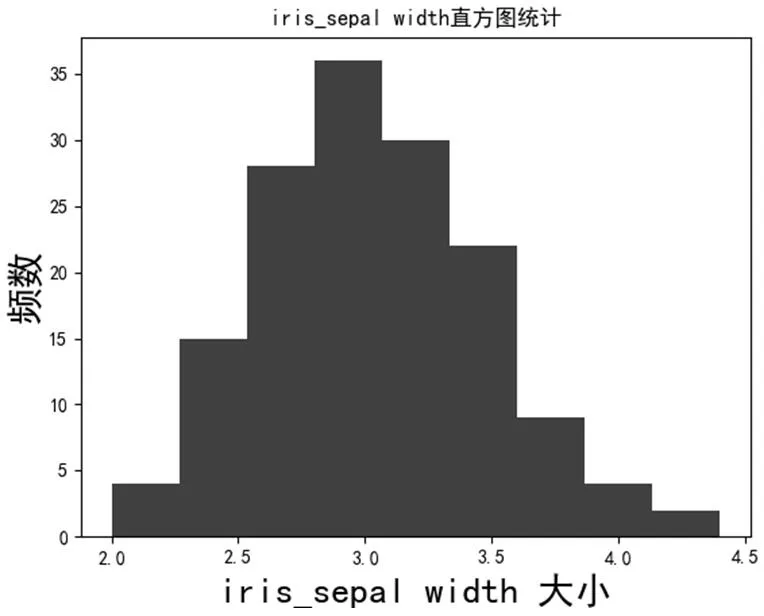
图2：iris_sepal width 直方图统计

（4）重复进行（2）（3）步骤，得到峰值集合F，取F 相同列得到K 个初始中心点

优化后的K-means 算法一次得到一个峰值，共计算K 步，称之为阶梯K-means 算法。直方图峰值的搜寻是对密度区间的预估计，通过上述方法得到的初始中心点，大多数是分布于聚类中心位置，远离聚类集合的边缘。

4 实验分析

本篇论文中的数据来自UCI 数据库的 Iris数据，进行了实验分析。

UCI 数据库的数据均为真实数据，常用来检验聚类算法的优劣。Iris 数据是鸢尾花的四个属性，分别是萼片长度（sepal length），萼片宽度（sepal width），花瓣长度（petal length）和花瓣宽度（petal width），分别使用 第1、2 维sepal 数 据，第3、4 维petal 数据和一共四维Iris 数据三组实验数据。直方图的分组数为s=9，对于传统K-means 算法、K-means++算法以及优化后的K-means 算法对上述三种数据进行聚类。聚类迭代次数和聚类正确率是聚类性能指标判断的标准。由于传统K-means 算法和k-means++算法随机选取初始聚类点，每次算法运行的结果有很大的不同，所以仿真150 次，取迭代次数和正确率的平均值。实验结果如表1所示。

由表1可以很明显的看出，在Iris 实验数据上，优化了初始聚类中心点后，迭代次数明显减少，对于高维度的数据，聚类正确率也有提高。图1、图2分别展示了iris sepal 在长度和宽度上的直方图的绘制情况，其中横坐标代表irissepal 的长度，纵坐标代表频数。

5 结束语

本文算法能够根据给定的K 值，较快的得到初始聚类中心，能够很有效的减少迭代次数，得到的聚类结果很接近真实数据。在较低维度下迭代次数的减少不是好很明显，在高维度下能够很明显的减少迭代次数，减少复杂运算。从上面的结果看，虽然能够减少迭代次数，但是在准确率上还是有改进空间。