Kalman 滤波在ECT 图像重建中的应用

文/霍启正

ECT 技术发展于上个世纪80年代，根据电容在通电时可以产生电磁场原理对工业管道中多相流体进行在线监测，在不接触管道内部流体情况下能够进行监测而且成本低的优点，为现代工业生产中多相流体的在线测量提供了一种新的测量方式。

ECT 技术主要分为两个问题：正问题和反问题。解析法及数值计算法为求解前者的主流方法。反问题是ECT 图像重建最为关键的问题，这是比较突出的病态求解问题，该问题制约了ECT 的发展。ECT 图像重建算法主要包括两大类：代数法和迭代法。代数法主要有线性反投影算法(LBP)、Tikhonov 正则化算法等；迭代算法包括Landweber 迭代算法、Kalman 滤波迭代算法等。代数类算法可以保证图像重建的实时性，迭代类算法可以增强图像重建精度。为提高ECT 图像重建质量，本文提出了一种在采集的原始数据中添加5%、10%和15%的高斯白噪声，然后分别使用Landweber 算法和Kalman 滤波算法进行图像重建。

1 成像原理

电容层析成像技术是近年来一种成本低，操作简单具有很高实用性的成像技术。ECT系统如图1所示。

ECT 系统可以分为三部分：

（1）电容传感器，一般有8 电容，12 电容和16 电容空间敏感阵列电极；

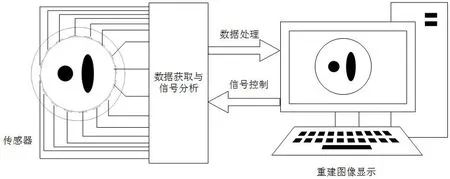
图1：ECT 系统原理框图

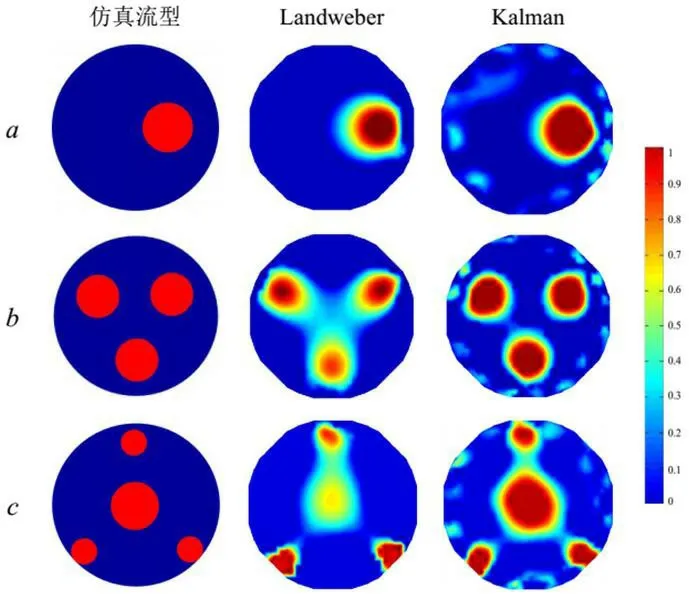
图2：加入5%的噪声成像

（2）数据采集系统，采集系统进行测量域的电容值获取，并将模拟信号转变为数字信号，发送至计算机处理端；

（3）图像重建系统，采用相适的图像重建算法，对被测对象某一截面的图像有针对性的重建。图像在重建过程中可以进行进一步的分析调整，并实现对其它参数的测量记录。

2 图像重建算法

ECT 系统模型如式（1）所示：

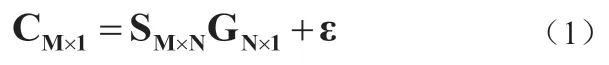
式中，C 为电容测量值，S 为灵敏度系数矩阵，G 为图像灰度矩阵，M 为独立测量数，N 为场域内剖分网格单元数，ε 为系统以及环境所存在的噪声。

2.1 Landweber算法

Landweber 迭代算法基于最速下降法选择负梯度方向为迭代方向，其法迭代公式为：

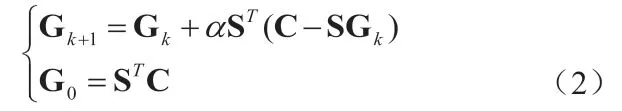
式中，Gk为第k 步迭代的图像灰度值，G0即为图像灰度原始值（该值经由灵敏度系数法得出），α 为迭代因子。

2.2 Kalman滤波算法

Kalman 滤波是一种最优估计方法，准则依据是选取最小均方误差为标准，在此基础上建立状态空间模型，模型与信号、噪声相关联，通过前一时刻的状态预测值和当前时刻的测量值来实现对当前时刻状态值的估计。将Kalman 滤波算法应用到ECT 图像重建上所建立的状态方程如式（3）所示：

式中，Gk为第k 步迭代的图像灰度值，Gk-1为前一步迭代图像灰度值。

由式（1）可以了解到图像灰度与电容测量值的状态方程如式（4）所示：

Ck为k 时刻的归一化电容测量值，Gk为k 时刻的图像灰度值，εk为作为k 时刻监测到的噪声，在实验环境中一般用协方差矩阵R表示，可以近似认为不变。Kalman 滤波算法的ECT 图像重建方程组为：

表1：空间成像误差（SC）

表2：相关系数（CC）

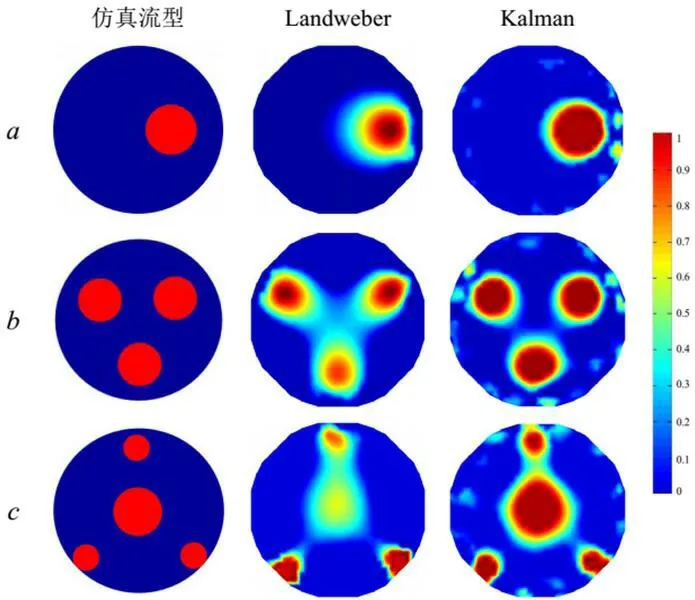
图3：加入10%的噪声成像

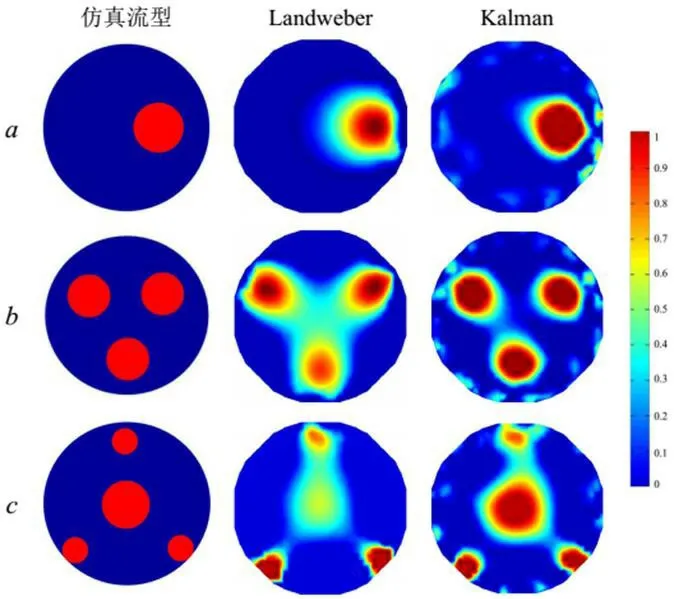
图4：加入15%的噪声成像

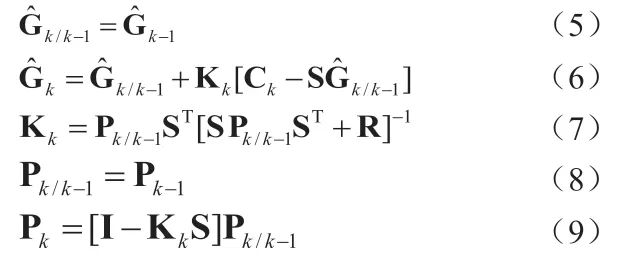
式（5-7）中，P 为最小均方误差矩阵，K为滤波增益矩阵。

在已知R 的情况下，给定初始值G0和P0，根据k 时刻的观测矩阵Ck递推出k 时刻的状态估计值。一般将非迭代算法的成像结果作为初始值G0，或者简单的取0。由于对第一次估计的估计均方误差P0没有先验值，一般取一个较大的常数矩阵。

Kalman 滤波算法的ECT 图像重建有两个过程：预测和校正。预测过程估计当前公式（5）的图像灰度值和公式（8）的误差方差矩阵，作为下一时刻的先验估计信息；核对纠正过程建立在先验估计的基础上，校正时也会会对比当前时刻电容值。通过两个数值的对比可以推出图像灰度最优时的预测值。

3 仿真实验及结果分析

本文采用Landweber 算法以及Kalman 滤波算法进行ECT 图像重建。仿真过程中，以油/气两相流为研究对象，设定了三种典型流型进行仿真实验，并分别命为名流型a、流型b 流型c。第一种考察重点在探究重建算法对位于管道壁和中心单一流型的重建效果，第二种考察对于复杂流型的重建效果，最后一种则重点考察对于在有其他流型影响下的管道中心灵敏度的成像效果。搜集参考数据可知油、气的相对介电常数（油为2.6、气为1），输入相关参数使用COMSOL 有限元软件测得测量电容值的相关数据，再使用MATLAB 进行ECT 图像重建，实现可视化的观测。

仿真过程中，Landweber 算法和Kalman滤波算法迭代次数取50 次，选取分别选取5%、10%和15%的噪声添加，仿真实验重建图像如图2，3，4 所示。

为定量评价重建图像质量，引入空间成像误差（SC）及相关系数（CC）进行评价，其定义为：

式中，Gsi，Gri分别为仿真原型和重建图像电常数分布矩阵，和分别为其均值，N 为剖分的正方形网格像素，N=812。

对图2，3，4 的重建图像，计算其对应的图像评价指标，如表1、2 所示。

从图1、2 以及表1、2 可以很明显的看出对于三种流型在相同迭代步数下，对数据采取归一化处理，并向电容值中加入相同的噪声后，Kalman 滤波算法重建图像质量更好，空间成像误差（SC）更小，相关系数（CC）更大。加入合适的噪声可以在一定程度上可以提高重建图像的质量。然而当加入15%的噪声时，Landweber 算法重建的流型a 和b 出现更多的伪影，流型c 出现较为严重的失真。尽管如此Kalman滤波算法仍能重建出较高质量的图像。重建后的图像先对于原图相似性也比较大。

4 总结

本文研究Landweber 算法和Kalman 滤波算法在ECT 图像重建的效果，并对结果进行对比。即分别研究了Landweber 算法和Kalman滤波算法在加入不同噪声的重建效果。仿真实验的数据以及结论表明：Kalman 滤波算法能够有效地过滤掉噪声在重建图像中的影响，当加入适当的噪声时，重建图像质量更高，空间成像误差更小，图像的相关系数更大；当噪声较大时，其依然能够重建出较高质量的图像，且图像与原始图像更相似。