基于粒子群算法的RBF神经网络零件表面缺陷分类

文/岳晓峰 刘天

1 引言

金属工件精加工表面缺陷主要分为三类：划痕、斑点、凹坑。金属工件表面缺陷常用分类方法有三种：人工神经网络分类法、支持向量机分类法和树状分段线性分类法。人工神经网络分类算法对非线性拟合问题表现突出，模拟大脑神经网络处理、记忆信息的方式进行信息处理。在1985年，Powell提出了多变量插值的RBF函数（Radical Basis Function，简称RBF）方法。1988年，Moody和Darken提出了一种神经网络结构，即RBF神经网络，属于前向类型的神经网络，它具有以任意精度逼近连续函数，特别适合于解决分类问题。RBF神经网络的缺点是，若RBF神经网络结构和参数选取不当，则会导致网络收敛慢甚至造成网络发散。针对标准RBF神经网络算法的不足，本文提出了一种基于粒子群算法改进的RBF神经网络的分类方法，利用粒子群算法优化RBF神经网络的基函数的中心xi、方差σ、输出权值ω，并对网络进行训练提高分类准确率。

2 RBF神经网络模型的建立

2.1 RBF神经网络结构

RBF网络的结构与多层前向网络类似，它是一种三层前向网络。第一层为输入层，由信号源节点组成；第二层为隐含层，隐含层的单元数量由所描述问题决定，隐含层单元的变换函数是对中心点径向对称且衰减的非负非线性函数；第三层为输出层，对输入模式的作用作出响应。从输入空间到隐含层空间的变换是非线性的，而从隐含层空间的输出层空间变换是线性的。由输入层、单一隐含层和输出层构成的RBF神经网络结构如图1所示。

RBF神经网络的激活函数一般使用RBF函数（如Gaussian函数）作为激活函数，以输入向量和权值向量之间的距离||dist||作为自变量的。RBF神经网络激活函数的一般表达式为：

2.2 RBF神经网络的学习算法

RBF神经网络学习算法需要求解的参数有3个：基函数的中心xi、方差σ、隐含层到输出层的权值ω。根据RBF函数中心选取的方法不同，RBF神经网络有多种学习方法，如随机选取中心法、自组织选取中心法、有监督选取中心法和正交最小二乘法等。本文采用K-均值聚类方法，学习算法具体步骤如下。

（1）网络初始化。

随机选取h个训练样本作为聚类基函数中心xi(i=1,2,…,h)。

（2）将输入的训练样本集合按最近邻规则分组。

按照xp与中心为xi之间的欧式距离将xp分配到输入样本的各个聚类集合ϑp(p=1,2,…,P)中。

（3）重新调整基函数的聚类中心。

计算各个聚类集合ϑp中训练样本的平均值，即新的基函数聚类中心xi，如果新的基函数聚类中心不再发生变化，则所得到的xi即为RBF神经网络最终的基函数中心，否则返回①，进入下一轮基函数中心的求解。

（4）求解方差σi。

RBF神经网络的基函数为Gaussian函数，因此方差σi可由下式求解。

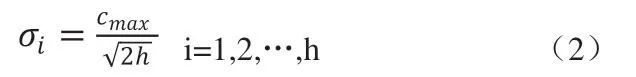
式中，cmax为所选取聚类中心之间的最大距离。

（4）计算隐含层和输出层之间的权值。

隐含层至输出层之间神经元的连接权值可以通过最小二乘法直接求得ω，计算公式如下。

2.3 RBF网络分类器的设计

图2：RBF神经网络分类流程图

图3：PSO算法流程图

在RBF神经网络结构图中，输入层到隐含层的权值是1，隐含层的激活函数为径向基函数，关键要求解出基函数的中心xi、方差σ、隐含层到输出层的权值ω。首先运用K-均值聚类方法确定基函数的中心xi，并通过公式（2）的计算求解出方差σi，由公式（3）求得隐含层到输出层的权值ω。由分类数决定输出节点数。将标准RBF神经网络应用于金属工件表面缺陷分类处理。金属工件表面缺陷分类3类，那么划痕的期望输出向量为L1（1,0,0），斑点的期望输出向量为L2（0,1,0），凹坑的期望输出向量为L3（0,0,1）。经过以上步骤，便构建完成RBF神经网络分类器的设计，RBF神经网络分类器的分类流程图如图2所示。

图4：PSO改进的RBF神经网络分类流程图

3 基于粒子群算法改进的RBF神经网络模型的建立

3.1 粒子群算法

粒子群算法，也称粒子群优化算法或鸟群觅食算法（Particle Swarm Optimization），是由J. Kennedy和R. C. Eberhart等提出的一种新的进化算法。在PSO算法中每个优化问题的潜在解都可以想象成搜索空间中的一只鸟，称之为“粒子”。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己，第一个极值是粒子本身所找到的最优解，这个解叫作个体极值pbest；另一个极值是整个种群当前找到的最优解，这个极值是全局极值gbest。粒子群算法的流程图如图3所示。其具体过程如下

（1）粒子群初始化，包括群体规模N，每个粒子的位置xi和速度vi。

（2）计算每个粒子的适应度值Fit[i]。

（3）用适应度值Fit[i]和个体极值pbest(i)比较，若Fit[i]>pbest(i),则用Fit[i]替换掉pbest(i)。

（4）用适应度值Fit[i]和全局极值gbest(i)比较，若Fit[i]>gbest(i),则用Fit[i]替换掉gbest(i)。

（5）根据公式：

式中c1，c2为学习因子，更新每个粒子当前的速度和位置。

（6）如果满足结束条件（寻找到个体极值pbest和全局极值gbest或者达到最大循环次数）退出，否则返回（2）。

表1：分类准确率

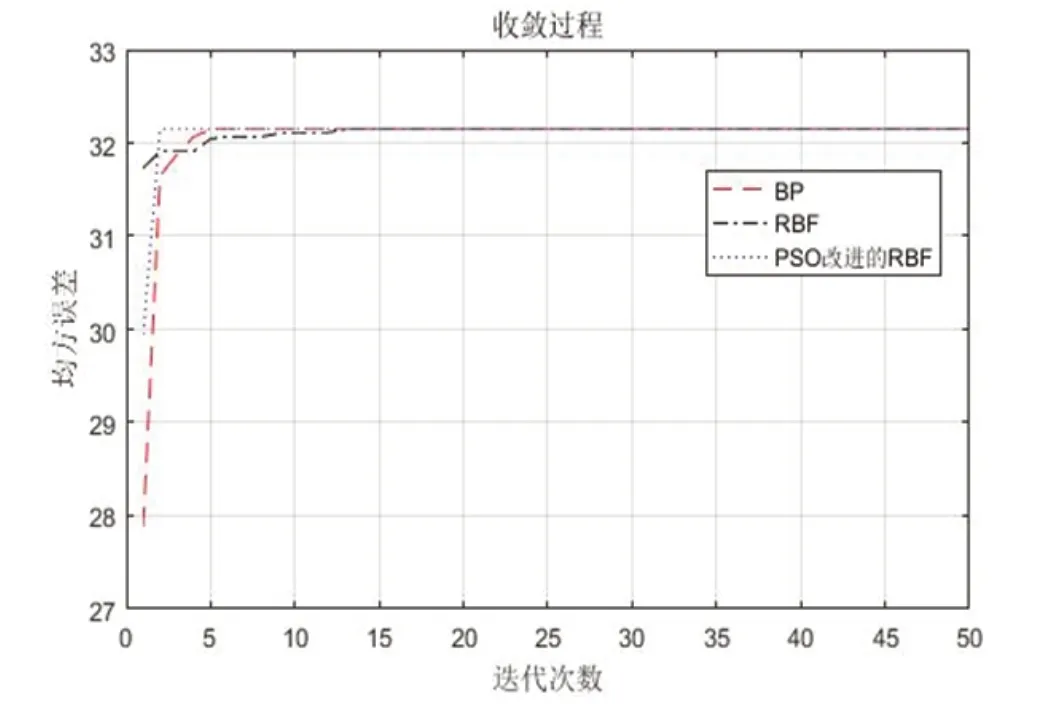
图5：3种方法性能对比图

3.2 权重改进的粒子群算法

PSO算法最大的优点是不需要调节过多的参数，但是算法中的群体规模N、惯性权重ω、加速度常数c1和c2却直接影响算法的性能和收敛性。其中惯性权重ω是最重要的参数。增大ω的值可以提高算法的全局搜索能力，减小ω的值可以提高算法的局部搜索能力。常见的PSO算法有自适应权重法、随机权重法和线性递减权重法等。本文采用线性递减权重法确定PSO算法中的惯性权重。针对PSO算法容易早熟及后期容易在全局最优解附近产生振荡现象，采用了线性递减权重法，即使惯性权重依照线性从大到小的递减，其变化公式为：

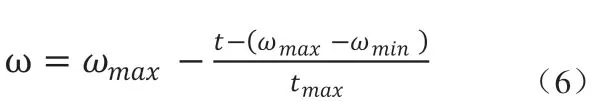
式中ωmax为惯性最大值；ωmin为惯性最小值；t为当前迭代次数。

线性递减权重法的计算步骤如下：

（1）随机设置各个粒子的速度和位置。

（2）评价每个粒子的适应度，将粒子的位置和适应值储存在粒子的个体极值pbest中，将所有pbest中最优适应值的个体位置和适应值保存在全局极值gbest中。

（3）更新粒子位移和速度：

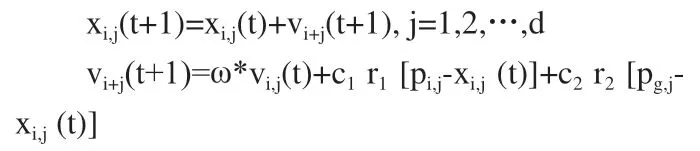
（4）更新权重：

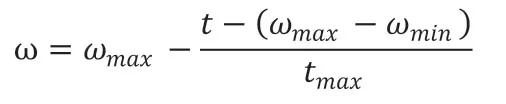
（5）将每个粒子的适应值与粒子的最好位置比较，如果相近，则将当前值作为粒子最好的位置。比较当前所有的pbest和gbest，更新gbest。

（6）当算法达到其停止条件，则停止搜索并输出结果，否则返回（3）继续搜索。

3.3 基于PSO改进的RBF神经网络分类算法实现

基于PSO 的RBF神经网络分类具体过程：

（1）读取输入样本和测试样本。

L1，L2，L3分别表示划痕、斑点、凹坑。每种缺陷的训练样本和测试样本各100幅图片。

（2）数据归一化处理。

在建立神经网络之前需要对训练样本和测试样本数据进行归一化处理，提高神经网络的收敛速度和泛化能力，同时增加每个样本之间的关联信息，使其拟合效果更好。实验中将数据归一化到[0,1]之间并找出样本X中的最大值Xmax和最小值Xmin，用如下公式计算：

Xi表示归一化后的数据，这样所有的数据都在[0,1]之间。

（3）RBF神经网络核函数参数的优化。

初始化粒子群及RBF神经网络，建立PSO算法中粒子与神经网络连接权值之间的映射；计算各粒子之间的适应值，将神经网络的方差作为PSO算法的适应函数，适应度函数值越大说明粒子的位置越好，其公式如下：

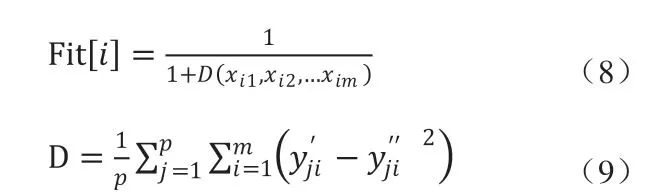
式中Fit[i]为第i个粒子的适应度值，D为神经网络的方差，p为训练样本总数，m是输出层的节点数，为实际输出值，为期望输出值；根据公式（4）和（5）更新粒子的速度和位置；重复上述步骤，直到找到粒子的最优解或者最大循环次数。

（4）运用经过PSO改进后的RBF神经网络对测试样本进行缺陷分类，分类流程图如图4所示。

图7

4 实验结果比较与分析

本文通过MATLAB R2016a软件进行编程，为了验证算法的有效性，首先使用标准RBF神经网络算法和PSO改进的RBF神经网络算法以及之前研究的BP神经网络算法进行性能对比实验，实验结果如图5所示。从图中可以看出在取得相同均方差时，PSO改进的RBF神经网络所需的迭代次数更少。

为验证程序的稳定性，将程序运行20次求得迭代次数平均值，如图6所示。

运用RBF神经网络、PSO改进的RBF神经网络和BP神经网络对金属工件表面的缺陷进行分类。采集含有缺陷的图片300幅，其中含有划痕、斑点、凹坑三种缺陷的图片各100幅。三种典型缺陷图片如图7所示。

对抽取的测试样本进行试验，分类结果如表1所示。

从表1中可以看出，划痕的分类识别准确率最高，达到97.8%，其次是斑点和凹坑，缺陷的平均识别率在94%。为证明本文中PSO改进的RBF神经网络分类方法优于RBF神经网络和BP神经网络分类方法，进行对比试验。采集含有缺陷的图片300幅，其中含有划痕、斑点、凹坑三种缺陷的图片各100幅，统计结果如图8所示。

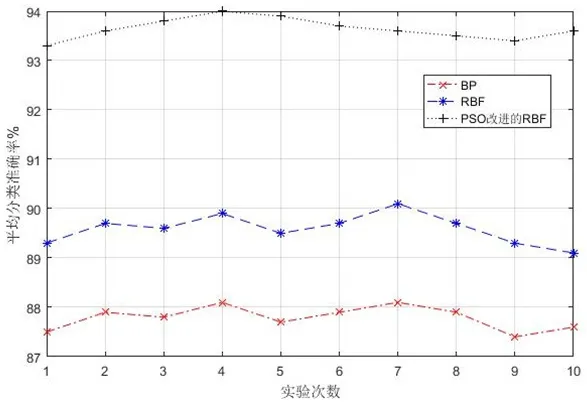
图8：分类方法对比实验

5 结论

本文应用PSO算法对RBF神经网络基函数的中心xi、方差σ、隐含层到输出层的权值ω进行训练寻求最优值，消除了人为因素选取RBF神经网络中心参数导致网络收敛慢甚至造成的网络发散问题。在标准PSO算法的基础上引进线性递减权重法对ω进行优化，提高了PSO算法的收敛速度和精度。对比实验表明PSO算法改进的RBF神经网络比标准RBF神经网络和BP神经网络分类识别准确率有较大提高。