采用混合驱动的精梳机分离罗拉传动机构
2019-04-25杨海鹏李新荣吕鹏飞王振宇
杨海鹏, 李新荣, 吕鹏飞, 王振宇
(1. 天津工业大学 机械工程学院, 天津 300387; 2. 天津市现代机电装备技术重点实验室, 天津 300387)
目前,高效能精梳机要求分离罗拉在每分钟之内完成600次以上的“倒转-正转-基本静止”的周期性运动,其传动机构的性能将直接影响棉网搭接质量以及车速的提高[1]。当前,国内市场上精梳机分离罗拉传动机构大都采用连杆机构或凸轮机构与差动轮系相结合的组合机构,其传动链复杂,在高速运动时会产生剧烈振动,影响车速的进一步提高及棉网的搭接质量。同时要想改变分离罗拉的输出运动特性,就需要改变传动机构的结构和尺寸参数。针对此问题,对于传动机构的研究,任家智等[2-3]从动力学角度出发,对传动结构进行平衡优化;国外企业则采用计算机辅助过程优化设计(CAPD)技术对连杆结构的尺寸及轮系齿数配比进行优化[4]。但随着车速的提高,机构的优化效果已经越来越不明显,机构的创新设计便成为关键。2003年,上海一纺机械有限公司提出了使用伺服电动机直接驱动分离罗拉的方案[5],减少了中间环节,理论上可进一步提高车速。但该方案要求电动机在高速下快速完成正转和反转运动,对伺服电动机负载能力要求高,伺服电动机依赖于进口,至今仍未得到推广。
现代机构学中“混合输入机构”的概念于20世纪90年代初由英国学者Tokuz等[6-7]首次提出,其混合驱动思想近些年引起国内外广泛关注[8-9]。混合驱动通过2个可控电动机驱动二自由度合成机构,即可将2个动力输入合成1个输出,通过伺服控制器对电动机的输入规律进行调节,能够改善电动机输出的动态性能[10],为解决传动机构输出规律多样性、柔性化与高速度、高承载力之间的矛盾提供了理论依据,为现代机构的创新设计提供了新的理念[11]。本文提出基于混合驱动的分离罗拉传动机构,根据精梳工艺要求,采用优化拟合的方法求得理想的分离罗拉运动规律,将其合理地分配到2个动力源,实现双伺服电动机单向转动驱动分离罗拉。
1 分离罗拉运动过程分析
1.1 分离罗拉运动工艺分析
精梳机以锡林轴旋转1周作为1个工作周期。在1个工作周期中,将锡林轴的运动分成40等分,每等分称为1个分度。在精梳过程中,分离罗拉与其他机件按照一定的分度关系进行相应的配合运动,分离罗拉在不同分度时的位移示意图如图1所示。可知:F0分度时,分离罗拉开始倒转;Fd1分度时,锡林末排针随锡林轴转动到达其与分离罗拉最紧隔距点,分离罗拉倒转量为Sd1;Fd分度时,分离罗拉倒转量达到最大,倒转速度减为0,将开始正转,分离罗拉倒转量为Sd;Ff分度时,分离罗拉正转速度与钳板摆动速度达到分离牵伸要求,须丛开始分离,分离罗拉正转量为Sf1;24分度时,钳板运动到最前位置,精梳须丛的分离工作完成,分离罗拉在精梳须丛分离阶段正转量为Sf;Fj分度时,分离罗拉正转量为Sy,此时分离罗拉开始静止直到F0分度时进入下一个工作周期。
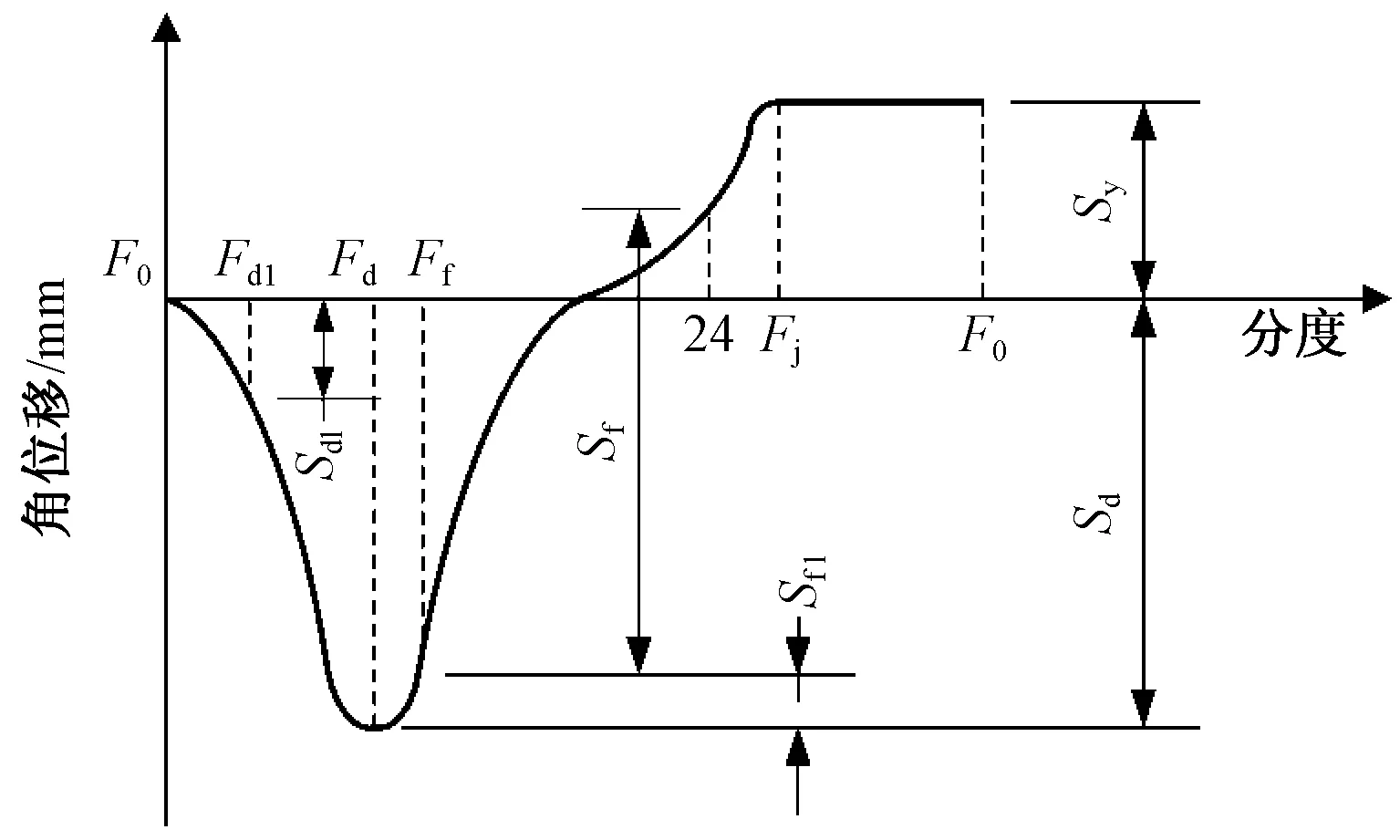
图1 分离罗拉运动位移示意图Fig.1 Displacement diagram of detaching roller
通过分析精梳过程中分离罗拉与顶梳、钳板、锡林等机件的运动配合关系,按照精梳机对分离罗拉运动的要求计算出关键点的分度值及对应的位移量,并在某一机型上进行实际的求解[12],绘出分离罗拉运动过程中倒转、正转等关键点的分布情况,如图2所示。
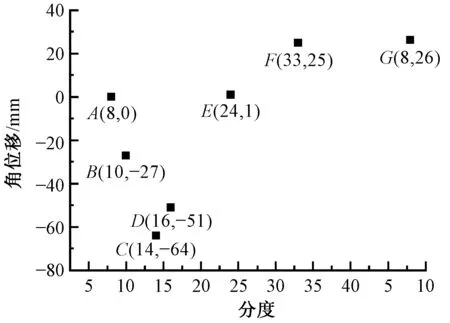
图2 分离罗拉位移曲线关键点分布图Fig.2 Distribution diagram of key points of detaching roller displacement curve
1.2 分离罗拉运动曲线拟合
分离罗拉传动机构受限于机械结构的束缚,由于机械机构驱动的分离罗拉运动曲线并不是最优的,故可在满足精梳工艺要求的条件下对传统机械式传动的分离罗拉运动曲线进行优化。通过分离罗拉“倒转-顺转-基本静止”运动状态过程中的位移关键点即可拟合出1条满足分离罗拉运动规律的曲线。为方便研究,对图2中7个点进行单位转换,得到关键点的坐标值如表1所示。
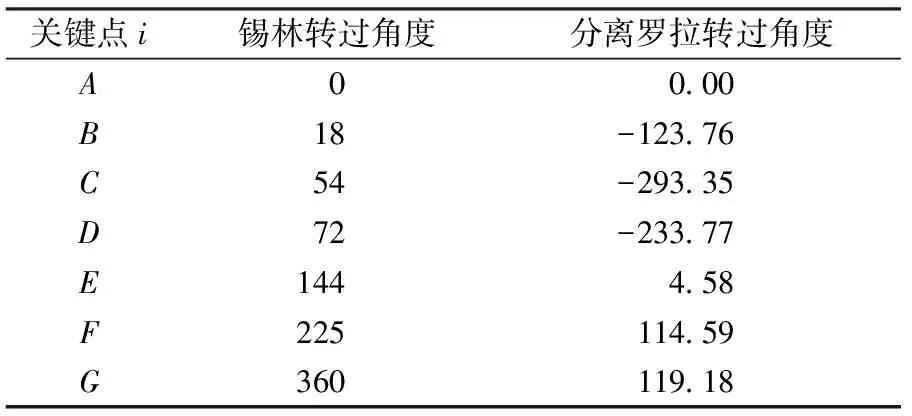
表1 分离罗拉运动曲线关键点Tab.1 Key points of detaching roller motion curve (°)
MatLab优化工具箱为曲线拟合提供了便利的求解算法,借助优化工具箱中的非线性优化函数fmincon对表1中的关键点进行优化拟合。其调用格式为:x=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,@nonlcon)。
1.2.1变量设计
通过对分离罗拉运动规律的研究,在对多组函数曲线形态研究的基础上,选取一次函数与六阶傅里叶函数相加的组合函数作为曲线的近似函数,即:
φ(θ)=kθ+a0+a1cos(ωθ)+b1sin(ωθ)+a2cos(2ωθ)+b2sin(2ωθ)+a3cos(3ωθ)+b3sin(3ωθ)+a4cos(4ωθ)+b4sin(4ωθ)+a5cos(5ωθ)+b5sin(5ωθ)+a6cos(6ωθ)+b6sin(6ωθ)
式中:θ为锡林轴分度盘转动角位移,(°);k、ω、ai(i=1~6)、bi(i=1~6)为式中的系数变量,即待拟合的设计变量。
1.2.2目标函数
利用最小二乘法,使所拟合的函数与样本点之间的误差平方和最小,故可列出目标函数:
minF(θ)=∑(Φθ-Si)2
式中:Φθ为分离罗拉角位移曲线函数,其中θ取值为0°、18°、72°、54°、144°、225°、360°;Si(i=A~G)为分离罗拉关键点角位移,(°)。
1.2.3约束条件
为满足运动的周期性与连续性要求,在1个周期内曲线的开始与结束处添加约束。
1)在θ为0°和360°处拟合曲线的角速度相等:
φ′(0°)=φ′(360°)
2)在θ为0°和360°处拟合曲线的角加速度相等:
φ″(0°)=φ″(360°)
3)在θ为0°和360°拟合曲线的跃度相等:
φ‴(0°)=φ‴(360°)
1.2.4优化计算及结果
经过多次迭代计算,曲线与7个关键点中误差最大值为10.235°,完全满足精梳工艺要求。拟合所得各系数变量值如表2所示。
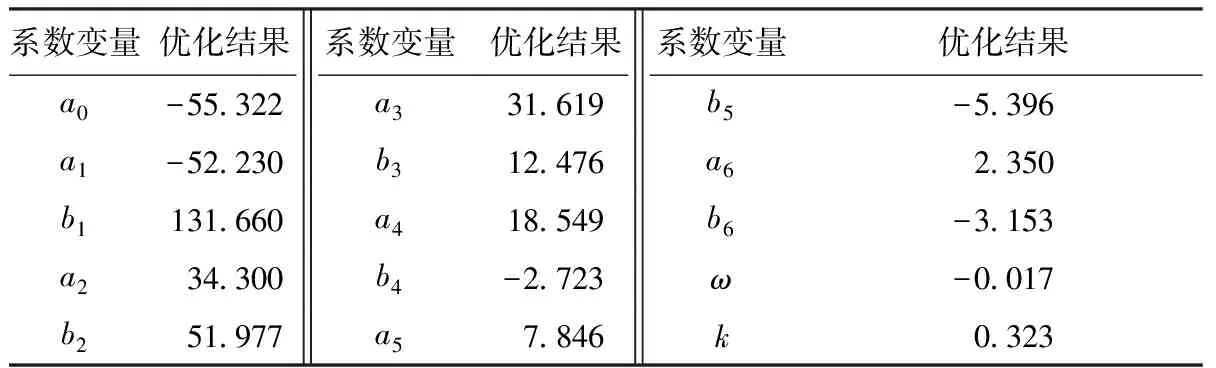
表2 计算得到的各变量的值Tab.2 Value of variables obtained from calculation
根据以上结果即可得到分离罗拉角位移与锡林轴上分度盘角位移之间的关系,通过单位转换得到分离罗拉角位移与时间之间的关系,然后对其求一阶、二阶和三阶导数便可得到分离罗拉运动的角速度、角加速度及跃度。当锡林转速为600钳次/min 时,在MatLab中绘制分离罗拉的运动规律图如图3所示。
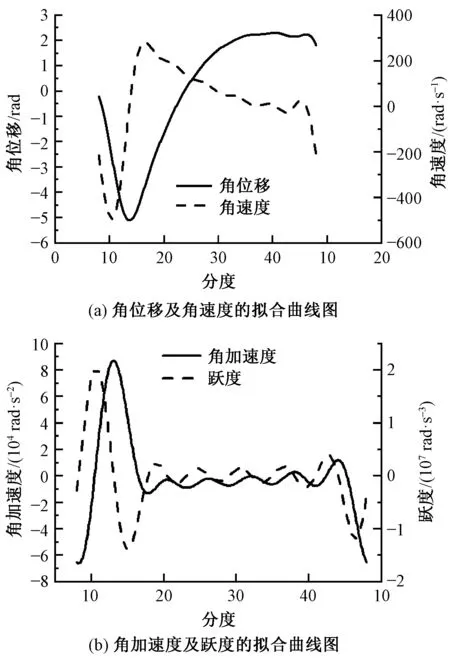
图3 分离罗拉的运动规律图Fig.3 Movement law of detaching roller. (a) Fitting curve of angular displacement and angular velocity; (b) Fitting curve of angular acceleration and jerk
由图3可知,拟合得到的角速度、角加速度及跃度曲线满足运动的周期性、连续性要求,其中,跃度曲线的连续性表明在分离罗拉运动过程中角加速度不会存在突变,将保持相对稳定的运行状态。同时,位移曲线表明其能够保证纤维须丛的分离、接合,因此,通过优化拟合所得到的分离罗拉运动工艺曲线是理想的。
1.3 分离罗拉运动动力分配
混合驱动机构是可控机构的一种[13],其采用 2个可控电动机作为驱动元,将2个输入运动通过 1个二自由度运动机构合成所需运动规律的输出运动[14]。新型高效能精梳机分离罗拉运动参数影响着分离接合效果及棉网的搭接质量,通过适度调整可使得精梳输出具有柔性[15],故可采用混合输入进行可控驱动。采用混合输入驱动最重要的就是合理的输入2个动力源,通过上文对输出运动即分离罗拉运动规律的分析,根据混合驱动机构的逆运动学分析即可将动力合理地分配到驱动系统中的2个伺服电动机上,即角速度的进一步分配,从而得到2个伺服电动机的运动规律。
1.3.1角速度分配
该混合驱动机构的设计是将2个伺服电动机的单向转动输入合成为1个输出运动,因此,可将求得的分离罗拉运动规律分配到2个输入端,即把分离罗拉的角速度合理分配到2个输入端,并保证2个输入端角速度是单向的。根据分离罗拉角速度与时间之间的关系,可将分离罗拉的输出角速度ωn(rad/s)看作2个电动机对应角速度ω1(rad/s)、ω2(rad/s)的代数和,即ωn=ω1+ω2。再通过差动轮系相关传动比即可得到2个电动机实际所需要的转速。
由图3可求得分离罗拉角加速度曲线上绝对值最大值为494.9 rad/s2,故可将曲线上下平移495个单位长度,再乘以各自的1/2,即可得到2条函数值分别大于零、小于零的曲线,作为2个伺服电动机对应的角速度曲线,能够保证2个伺服电动机的单向传动的要求。这2个伺服电动机对应的角速度曲线如图4所示。
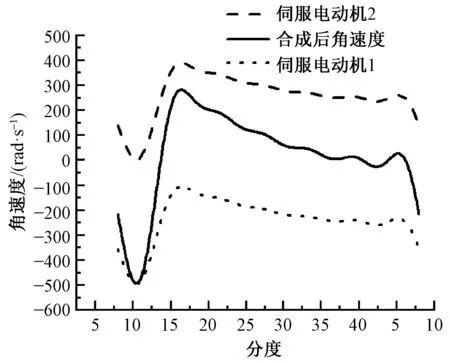
图4 2个伺服电动机对应速度曲线图Fig.4 Speed curve of two servo motors
1.3.2差动轮系理论分析
设行星齿轮传动机构中差动轮系的2个输入构件a、b和输出构件H的角速度分别为ωa(rad/s)、ωb(rad/s)和ωH(rad/s),其结构简图如图5所示。根据相对角速度之比得:
(1)
(2)
将式(1)、(2)相加得
(3)
由式(1)~(3)可得
(4)
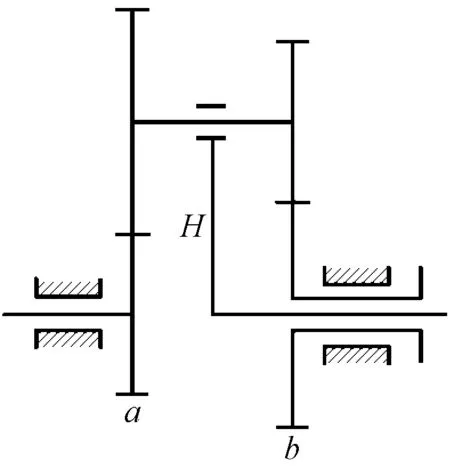
图5 差动轮系结构简图Fig.5 Schematic diagram of differential gear system
同理可得到ωb、ωH的表达式,则该差动轮系的角速度关系式为
(5)
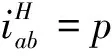
(6)
由运动学方程可看出,在差动轮系中只要知道3个构件中2个构件的转速,便可求出第3个构件的转速,从而也可求出任意2个构件之间的传动比。
本文传动机构中以齿轮Z1和中心轮Z3作为输入,齿轮Z8作为输出。驱动示意图如图6所示。各齿轮齿数分别为Z1=80,Z2=95,Z3=32,Z4=22,Z5=29,Z6=25,Z7=87,Z8=28。
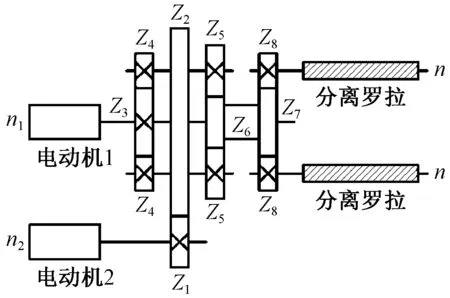
图6 混合驱动机构图Fig.6 Hybrid drive mechanism diagram
根据混合驱动机构各齿轮的齿数计算出差动轮系传动比,结合式(6)推导出2个输入转速n1(rad/s)、n2(rad/s)与输出转速ωn(rad/s)之间的关系式:
ωn=-5.243 3n1-1.798 9n2
(7)
为方便起见,令ωn=ω1+ω2,即
(8)
则
(9)
根据前面角速度分配的2个伺服电动机对应的角速度ω1、ω2,即可计算出2个伺服电动机实际的驱动角速度n1、n2。伺服电动机的实际运动规律曲线如图7所示,并且2个电动机单向变速。
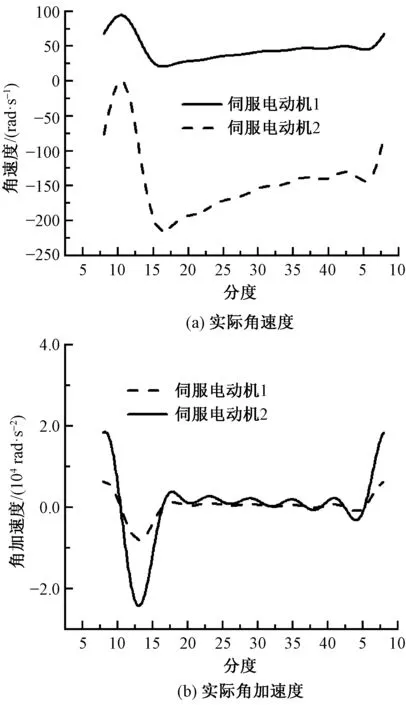
图7 伺服电动机角速度及角加速度实际运动规律Fig.7 Actual angular velocity and acceleration motion rule of servo motor. (a)Actural angular velocity;(b)Actural angular acceleration
相较于伺服电动机直接驱动分离罗拉系统,混合驱动系统可使伺服电动机在高速状态下避免正反转。在锡林转速为600钳次/min时,若采用伺服电动机直接驱动分离罗拉,由图3可知,电动机最大角加速度为87 020 rad/s2;而采用混合驱动方案,由图7 可知,2个伺服电动机中角加速度最大值为24 320 rad/s2。经计算,2个伺服电动机中角加速度最大值比伺服电动机直接驱动分离罗拉方案中的伺服电动机角加速度最大值减小了72.05%,故可有效减小伺服电动机驱动过程中的峰值功率和扭矩,从而降低对伺服电动机负载能力的要求。
2 仿真分析
Adams是以计算系统动力学为基础,包含多个专业模块和专业领域的虚拟样机开发系统软件。采用虚拟样机技术在产品的研发中可缩短研发周期,提高设计效率,在工业产品设计领域中得到了广泛的应用。
首先在Pro/E中建立差动轮系三维模型,然后将其导入到Adams中,进行各齿轮及驱动的定义,将分配好的角速度分别输入到2个伺服电动机中进行运动仿真,得到分离罗拉输出角速度曲线及加速度曲线如图8所示。
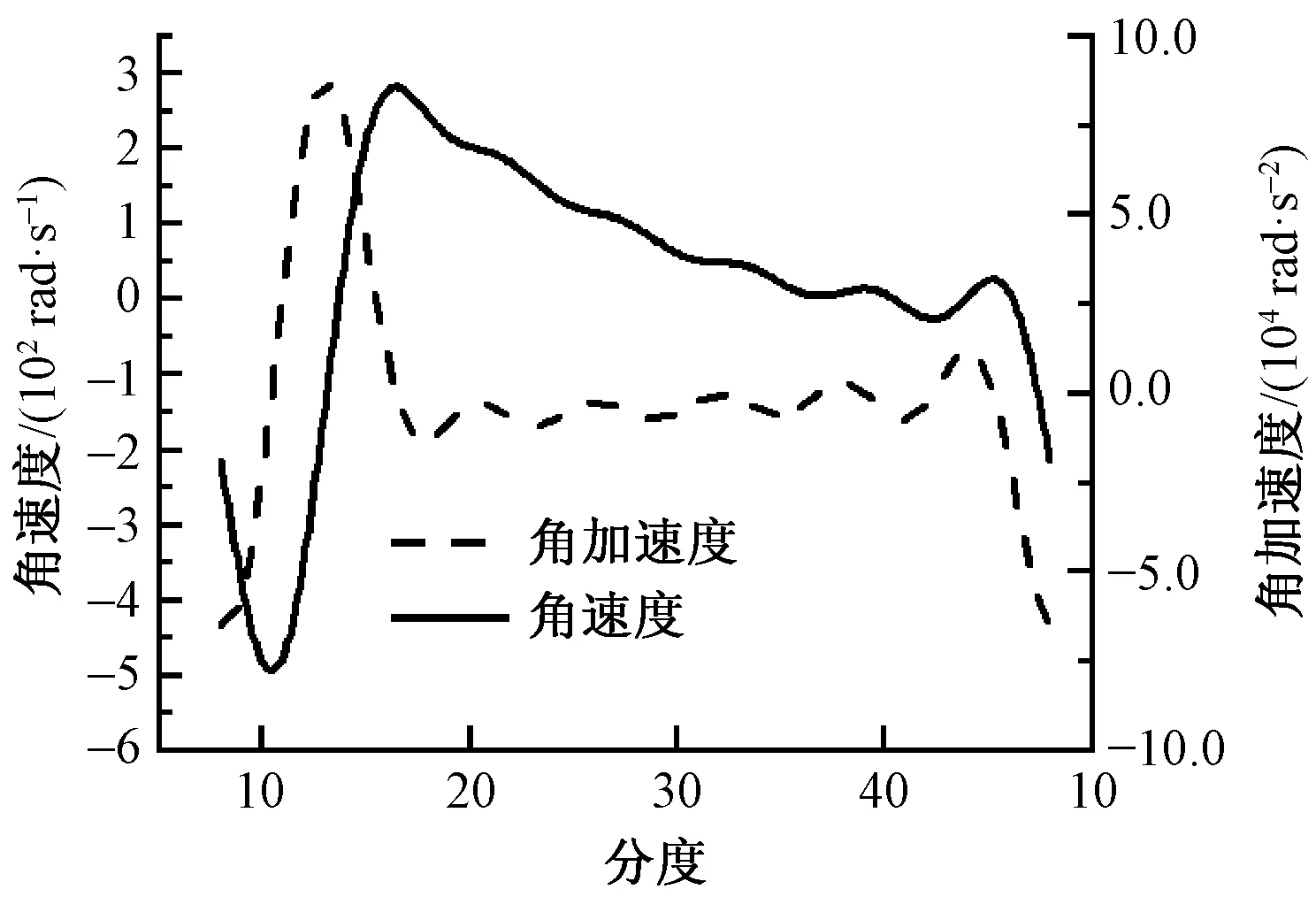
图8 Adams中输出的分离罗拉角速度及角加速度曲线Fig.8 Separation roller angular velocity and angular acceleration curve output from Adams
通过与MatLab所作角速度、角加速度图像对比可以发现,二者完全相同,从而验证了传动机构及动力分配方案的正确性。
3 实验验证
在对混合驱动机构进行计算机模拟验证的基础上,有必要对其效果进行样机验证。本文实验在多轴驱动精梳机实验平台上进行,该实验平台包括机械系统和控制系统。机械系统中,在车头处由伺服电动机通过减速器来驱动分离罗拉,车尾处由曲柄滑块机构来驱动钳板摆轴。其中,传动系统中行星差动轮系机构实物图如图9所示。控制系统中,通过MAESTRO多轴运动控制器、伺服数字驱动器、编写程序使得精梳机分离罗拉驱动电动机分别按照上述所分配的运动规律运转。按照精梳工艺要求开车,即可进行检测车速为600钳次/min时分离罗拉的运动状态。

图9 分离罗拉驱动机构实物图Fig.9 Physical drawing of detaching roller drive mechanism
实验完毕后,通过整理1个工作周期内实验平台角位移传感器所测得的分离罗拉运动数据,进行绘图并与计算机仿真图进行对比如图10所示。可知,实验所得到的角位移曲线与仿真所得的位移曲线结果非常接近,可满足精梳机分离罗拉分离、接合的工艺要求,从而验证了混合驱动方案的合理性。同时对比2条曲线可知,实验结果与理论值最大误差为14.06°。分析其原因是因为在实验过程中齿轮振动对分离罗拉运动产生了一定影响,特别是随着速度的提高,齿轮在啮合过程中产生的振动会越来越大,其对分离罗拉的运动状态的影响也随之增大。故以后可深入研究差动行星轮系,减小轮系振动对分离罗拉运动状态的影响。
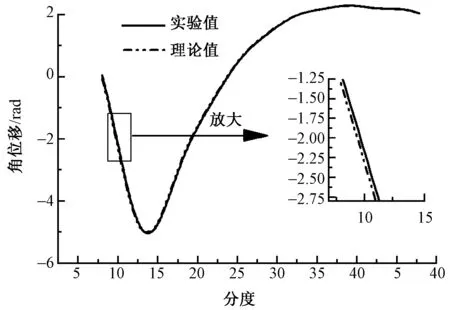
图10 精梳机分离罗拉角位移曲线图Fig.10 Displacement curve of detaching rollers of comber
4 结 论
本文通过分析分离罗拉的运动规律,采用混合驱动的方案,并进行动力的合理分配。然后使用虚拟样机技术仿真分析该方案的可行性,并采用实验验证其合理性。
1)基于最小二乘法思想,在MatLab中对分离罗拉运动过程中的关键点进行拟合得到1条优化曲线,其误差最大值是10.235°,完全满足精梳工艺要求。
2)所设计的混合驱动机构中,2个伺服电动机中角加速度最大值比伺服电动机直接驱动分离罗拉方案中的伺服电动机角加速度最大值减小了72.05%。
3)该混合驱动机构不但简化了中间复杂的传动链,消除了高速状态下由于惯性力引起的剧烈振动,可提高棉网搭接质量,而且使得整个驱动机构输出具有柔性,可根据不同纤维长度及梳理棉花种类对伺服电动机输入规律进行调节,具备一机多用的功能。
4)在进行曲线拟合以及动力源分配时,本文所采用的拟合和分配方法只是众多方法中的一种,更加适合的拟合方法以及更加合理的分配方案还需进一步研究。本文提出的基于混合驱动思想设计的分离罗拉传动机构,不但为设计高速精梳机打开了新思路,且为具有此类运动特点的场合提供了借鉴。
