基于水土耦合的降水沉降分析理论及应用
2019-04-25谈炎培
谈炎培,石 文,2
(1、佛山市铁路投资建设集团有限公司 广东佛山528000;2、佛山市轨道交通发展有限公司 广东佛山528000)
0 引言
城市地下空间开发涉及大量深基坑工程,在地下水丰富的地区进行基坑开挖时,需先进行工程降水。地下水位的降低将引起地层固结压缩,产生地表沉降,对周边建构筑物和环境造成严重影响。如上海地铁7 号线某车站降承压水诱发了最大达85 mm 的沉降[1];南京地铁2 号线某车站基坑降水导致邻近民宅发生沉降并损坏[1];荆州某大厦由于邻近基坑降水而引起主楼和裙楼出现宽达45 mm 的差异沉降裂缝[2]。由此可见,深基坑降水诱发的地表沉降相当普遍,已成为基坑工程的主要危害因素。
分析地表沉降的关键是所采用的降水沉降分析理论。已有理论分为非耦合理论和耦合理论两大类。非耦合理论以Terzaghi 理论、Gambolati 两步法理论为代表。Gambolati 等人对威尼斯沉降进行研究后提出了两步法理论[3,4];骆祖江等人[5]采用了Gambolati 两步法理论,对上海环球金融中心群井降水进行数值模拟。耦合理论则以Biot 理论[6]为代表,冯晓腊等人[7]利用Biot 固结方程对武汉市中山广场工程降水进行了计算;基于Biot 固结理论,陈锦剑等人[8]对上海一深水池工程的基坑外承压水降水进行了数值模拟,叶为民等人[9]以Hardening-soil 本构模型来探讨不同降水方案对地面沉降的影响,刘婧等人[10]利用有限元方法对上海世博500 kV 地下变电站基坑降水施工进行了分析。此外,对于普通降水井的实际降水效果,徐建邦等人[11]通过工程实例进行了总结;对于真空降水井的降水效果,肖瑞传等人[12]进行了数值计算分析。
总结已有研究现状,目前对基坑降水引起水位变化和地表沉降的研究已取得了较为丰硕的成果,但在以下方面仍可进一步完善:一是已有研究较少考虑孔隙水压缩性。根据Xie 等人[13]的分析,在地下水压较大的情况下,孔隙水压缩性对于地表沉降的计算结果有一定程度的影响。二是在已有耦合理论计算分析中,降水是通过在Biot 方程中引入源汇项的方式来实现的。由该方法得到的降水井附近的水位变化及地表沉降与实际有一定的偏差[14]。
本文根据已有研究成果,考虑孔隙水压缩性,获得基于水土耦合的降水沉降分析理论,并通过降水边界条件代替源汇项的方式来实现降水。利用有限元方法实现数值分析,通过对比工程降水的经典水位解析解,验证了该理论的正确性。最后利用该理论对某工程抽水试验进行计算分析,通过数值计算结果与现场实测水位、地表沉降的对比分析,验证了本文所提理论用于实际工程分析的适用性和合理性,为类似的工程应用提供参考。
1 降水沉降分析理论及验证
1.1 控制方程
对不同理论的渗流连续性方程进行分析,黄大中等人[15]曾提出以一个统一方程进行表述,并考虑了孔隙水压缩性。参照该方程中的水压缩性项,引入至Biot理论中,可得到考虑孔隙水压缩性的水土耦合降水沉降分析理论。由于篇幅限制,详细的推导过程见文献[14],此处不再列出。笛卡尔坐标下,控制方程为:

式中△:第1 式为渗流连续性方程,第2~4 式为平衡方程。2为Laplace 算子;H=z+Pt/γw为总水头(z、Pt/γw分别为位置水头和压力水头);u、v、w分别为三个方向上的位移;kx、ky、kz为三个方向上的渗透系数;γw为水的重度;n为孔隙率;β为水压缩系数;E为弹性模量;ν为泊松比;γ′为土的有效重度。
1.2 降水边界条件
如前所述,本文是通过降水边界条件配合相应的流量来实现降水。具体设置方法为:按照实际尺寸建立降水井计算模型,在降水井滤管段设置流量边界;在非滤管段设置不透水边界。可表示为:

式中:Sq为模型的降水边界;为Nabla 算子;n 为降水井滤管壁的外法向量;k 为渗透系数张量;nx、ny、nz分别为n 与三个坐标轴之间的方向余弦;Qp为井抽水流量;rp为降水井的截面半径;Lps为降水井滤管段长度。其余变量的含义与前述一致。
1.3 其他边界条件
1.3.1 位移边界条件
对于固定或指定位移值的边界,应采用位移边界条件,即在边界上直接指定3 个位移变量的值,可表示为:
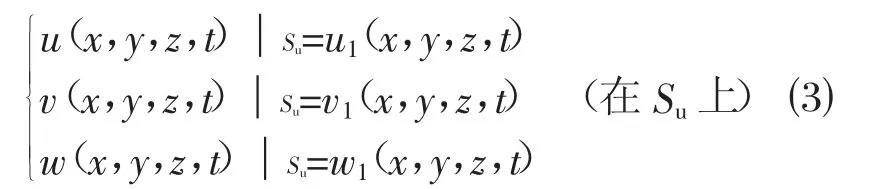
式中:Su表示模型的位移边界;u1(x,y,z,t)、v1(x,y,z,t)、w1(x,y,z,t)分别为位移边界Su三个方向上的已知位移函数。
1.3.2 应力边界条件
当降水场地范围内有荷载作用时,应采用应力边界条件,即在相应边界上直接指定荷载值(以面力形式),可表示为:

式中:Sσ为模型的应力边界;μe=E/[2(1+ν)]和λe=Eν/[(1+ν)(1-2ν)]为拉梅常数;Fx、Fy、Fz分别为应力边界Sσ上的已知荷载函数,当边界上不受荷载作用时,荷载函数均为零。
1.3.3 水力边界条件
当模型的计算范围与稳定水体如江、河、湖泊等连通或需设置含水层的远端边界(工程降水时,远端不受影响)时,应采用水力边界条件,即在边界上指定水头值,可表示为:

式中:Sh为模型的水力边界;H0(x,y,z,t)为边界Sh上的已知水头函数。对于地下水位线所在位置,总水头H(x,y,z,t)组成部分中的压力水头为零,位置水头根据参考坐标系确定。
1.4 有限元数值实现
式⑴所示的控制方程为偏微分方程组,一般情况下无法获得解析解,只能诉诸于数值解。根据有限单元法原理,先利用变分法得到控制方程的等效积分弱形式,再通过单元离散、结点插值、数值积分、方程集总、方程求解等步骤,可获得问题的相应数值解。详细的有限元求解过程见文献[14],此处不再叙述。
1.5 与解析解的对比验证
单井降水的稳态和瞬态解析解分别为Dupuit 解和Theis 解。将本文理论的数值解与解析解进行对比,可验证该理论的正确性。降水井的最大水位降深为20 m,计算边界由降水井中心往外延伸300 m,稳态降水时长100 d,瞬态降水时长6 912 s。
数值解与解析解的结果对比如图1、图2 所示,可见,本文提出理论的数值解与已有的稳态解Dupuit 公式及瞬态解Theis 公式均相当吻合,这表明了所提出的理论是合理、正确的。
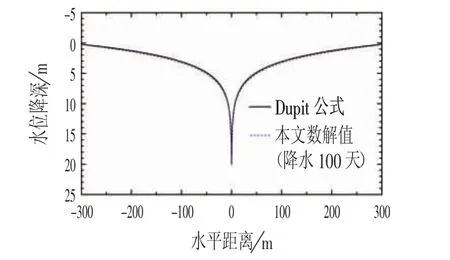
图1 数值解与Dupuit 解的对比Fig.1 Comparison between Numerical Solution and the Dupuit's Solution

图2 数值解与Theis 解的对比Fig.2 Comparison between Numerical Solution and the Theis's Solution
2 现场抽水试验应用
2.1 抽水试验概况
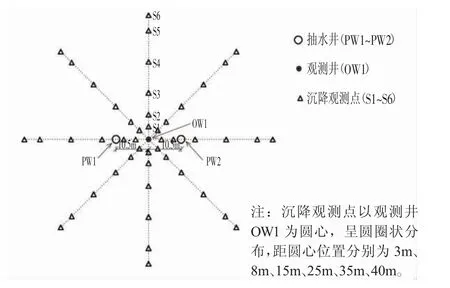
图3 降水井和沉降监测点布置图Fig.3 Layout of Pumping Wells and Settlement Measurement Points

表1 井结构参数Tab.1 Well Structure Parameter
某抽水试验场地位于上海虹桥综合交通枢纽工程试验一区,该交通枢纽的详细规划和布置可参考文献[14]。由于基坑面积大,水位降深较大,需在正式降水前先进行现场抽水试验。抽水试验的井位布置、沉降监测点布置、井结构参数如图3、表1 所示。场地土层分布及计算参数如表2 所示,其中第⑦层、第⑨层土分别为第Ⅰ、Ⅱ承压含水层。
2.2 有限元模型及参数
模型计算边界从井中心向外延伸500 m,模型长度为1 021 m,宽度为1 000 m,深度为85 m,网格划分如图4 所示。位移边界条件为底部固定,4 个侧向边界约束水平位移,顶部自由;水力边界条件为底部不透水,4 个侧向设为定水头边界模拟承压水补给,顶部自由排水;不受表面荷载作用,应力边界条件为0。
2.3 计算值与实测值对比
2.3.1 水位结果
图5a、图5b 分别为降水井PW1、PW2 双井抽水时和停止抽水后水位恢复阶段,观测井OW1 中计算与实测水位的对比。由图5a 可见,在抽水阶段,初期的水位快速下降,至2 000 min 以后,水位基本稳定;计算与实测水位反映的变化趋势一致,而且两者较为吻合。由图5b 可见,在水位恢复阶段(停止降水),水位在初期迅速恢复,然后恢复的速率慢慢降低,至3 000 min 以后,水位基本稳定;计算与实测水位的恢复趋势一致,虽在中期略有差异,但是差值不大。此外,计算与实测结果均反映,水位恢复速率比水位下降速率要小。

表2 土层分布及材料计算参数Tab.2 Soil Profile and Material Parameters for FEM Calculation

图4 有限元模型总体及局部视图Fig.4 Global and Local View of FEM Model
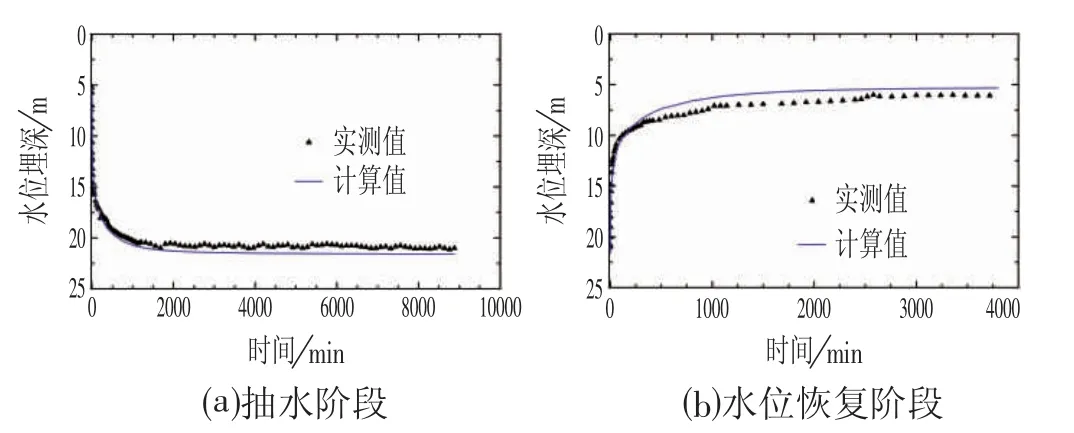
图5 计算与实测水位对比Fig.5 Comparison between Calculated and Measured Water Table
2.3.2 沉降结果
图6为与降水井不同距离的监测点上,计算与实测地表沉降值的对比。由图6 可见,随着抽水试验的进行,地层中孔隙水排出,土层固结压缩,地表沉降逐渐增大,计算值与实测值的趋势是一致的。距离降水井较近的监测点,计算与实测地表沉降的差值较小,结果更吻合;距离降水井较远的监测点,两者略有差距,计算沉降值偏大。此外,对比水位与沉降结果可发现,地下水位要比地表沉降更快趋于稳定,表明地表沉降的发生相对于地下水位下降存在一定的滞后性,沉降发展与水位不同步。地表沉降滞后于水位下降的情况在实际降水施工中普遍存在,计算与实测地表沉降均反映了这个特征。

图6 不同监测点计算与实测地表沉降对比Fig.6 Comparison between Calculated and Measured Ground Settlement at Different Measurement Points
上述对比分析表明,利用提出的降水沉降理论进行分析,水位结果相当吻合,地表沉降结果虽有差异但差值不大。计算分析结果合理可靠,适用于实际降水施工计算或预测。
3 结论
根据已有研究成果,推导得到了基于水土耦合的降水沉降分析理论,并用经典解析解验证了正确性。利用该理论对某工程抽水试验进行计算分析,通过水位、沉降的计算值与实测值对比来评价理论的适用性和合理性。主要结论如下:
⑴基于水土耦合框架,通过考虑孔隙水压缩性,并利用降水边界条件实现降水,可得到本文的水土耦合降水沉降分析理论。利用该理论的数值解与单井降水的稳态、瞬态解析解进行对比,验证了该理论的正确性。
⑵对某抽水试验进行计算分析,计算与实测水位反映的变化趋势一致,在抽水阶段两者相当吻合;而在水位恢复阶段,两者虽在中期略有差异,但是差值不大。计算与实测结果均反映了水位恢复速率比水位下降速率要小。
⑶计算与实测地表沉降的发展趋势一致,随着水位下降,沉降逐渐增大。距离降水井较近的监测点处,计算与实测地表沉降较为吻合,两者差值比距离降水井较近的监测点处的要小。计算与实测结果均反映了地表沉降滞后于水位下降,沉降发展与水位不同步。
⑷本文理论用于抽水试验的计算分析时,水位结果相当吻合,地表沉降结果虽有差异但差值不大。总体结果合理可靠,表明该理论适用于实际降水施工计算或预测。
