Determination of the Backward Predictability Limit and Its Relationship with the Forward Predictability Limit

Xuan LI,Ruiqiang DING∗,and Jianping LI

1State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics(LASG),Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China

2College of Earth Science,University of Chinese Academy of Sciences,Beijing 100049,China

3Laboratory for Regional Oceanography and Numerical Modeling,Qingdao National Laboratory for Marine Science and Technology,Qingdao 266237,China

4College of Global Change and Earth System Sciences(GCESS),Beijing Normal University,Beijing 100875,China

ABSTRACT In this work, two types of predictability are proposed—forward and backward predictability—and then applied in the nonlinear local Lyapunov exponent approach to the Lorenz63 and Lorenz96 models to quantitatively estimate the local forward and backward predictability limits of states in phase space.The forward predictability mainly focuses on the forward evolution of initial errors superposed on the initial state over time, while the backward predictability is mainly concerned with when the given state can be predicted before this state happens.From the results,there is a negative correlation between the local forward and backward predictability limits.That is,the forward predictability limits are higher when the backward predictability limits are lower,and vice versa. We also f ind that the sum of forward and backward predictability limits of each state tends to f luctuate around the average value of sums of the forward and backward predictability limits of suきcient states.Furthermore,the average value is constant when the states are suきcient. For diあerent chaotic systems,the average value is dependent on the chaotic systems and more complex chaotic systems get a lower average value.For a single chaotic system,the average value depends on the magnitude of initial perturbations. The average values decrease as the magnitudes of initial perturbations increase.

Key words: nonlinear local Lyapunov exponent, forward and backward predictability limit, negative correlation, average value

1. Introduction

The atmosphere is a complex nonlinear system,meaning that forecasts are sensitive to the initial state. Small errors in the initial state are amplif ied greatly in a short time, which means that the atmospheric predictability has a certain time limit,def ined as the predictability limit(Lorenz,1969a). Beyond the predictability limit, the prediction skill is so low that the forecast becomes useless. It is therefore important to study the predictability of the atmosphere,as this can inform operational forecasting.

The problem of atmospheric predictability was classif ied into two main types by Lorenz.The f irst type of predictability focuses on the growth of initial errors, and the second type is concerned with model errors. There has been much research into the two types of atmospheric predictability using nonlinear theory and numerical simulation (Thompson,1957; Lorenz, 1965, 1982, 1996; Chou, 1989; Nese, 1989;Yoden and Nomura, 1993; Ziehmann et al., 2000; Mu and Wang, 2001; Mu et al., 2002; Chen et al., 2006; Zou et al.,2006;Ding and Li,2007;Peng et al.,2011).

Dalcher and Kalnay (1987) pointed out that the doubling time of small errors is not a good measure of error growth because of its sensitivity to the method of extrapolation. Also,they suggested that the saturation or asymptotic value of root-mean-square error provides a better measure of the predictability limit.Ding et al.(2008)used the mean local relative growth of initial error(LRGIE)to quantify the local predictability limit of chaotic systems based on the nonlinear local Lyapunov exponent (NLLE) method. In their views, if the initial state xxx(t0) and initial perturbations δ(t) are given,the local predictability of the chaotic system will be lost after the mean LRGIE reaches an asymptotic value or saturation at the future state xxx(t1).Then,the evolution time from t0to t1is determined as the local predictability limit starting from the initial state xxx(t0).Here,we refer to this type of predictability as the local forward predictability,and the local predictability limit is called the local forward predictability limit.However,if a state xxx(t0) and initial perturbations δ(t) are f irst given,then how can this be determined when the given state can be predicted before it happens? We refer to this type of predictability problem as the local backward predictability. To quantify local backward predictability, f irst we need to f ind the corresponding initial state xxx(t-1)of the given state.When the corresponding initial state xxx(t-1)is found, the time from the state t-1to t0is determined as the backward predictability limit of the given state xxx(t0).Figure 1 shows the local forward and backward predictability of state xxx(t0).At the initial moment t0, the large number of initial errors δ(t) with the amplitude and diあerent directions are superposed on the initial state xxx(t0).When the mean LRGIE reaches saturation at moment t1, the local forward predictability limit of initial state xxx(t0)can be determined as t1-t0.If the large number of initial errors δ(t)with the amplitude and diあerent directions are superposed on the initial state xxx(t-1),the mean LRGIE reaches saturation at time t0. The local backward predictability limit of a given state xxx(t0)can be determined as t0-t-1.

The initial state xxx(t0)and perturbations δ(t)are the cause and the state xxx(t1)is the result in local forward predictability,while the given state xxx(t0)is the result and the corresponding initial state xxx(t-1) that is searched for is the cause in backward predictability. Therefore,the backward predictability is an inverse problem of the forward predictability.

Fig.1.Schematic diagram of local forward predictability(solid line)and backward predictability(dashed line)of the state xxx(t0).t0 is the moment of the initial state xxx(t0).t1 is moment of the future state xxx(t1)where the mean LRGIE superposed on the initial state xxx(t0) reaches saturation. t-1 is the moment of the corresponding initial state xxx(t-1)of which the mean LRGIE reaches saturation at the given state xxx(t0).The circle diameter is the initial error size.

The forward predictability focuses mainly on the forward evolution of initial errors superposed on the initial state over time, while the backward predictability is mainly concerned with how to f ind the corresponding initial state of the given state. When the corresponding initial state is found,the backward predictability limit of the given state is determined.Forward predictability has been studied intensively(Lorenz, 1965, 1969a, b; Leith, 1971; Dalcher and Kalnay,1987; Farrell, 1990; Mukougawa et al., 1991; Toth, 1991;Yoden and Nomura, 1993; Simmons et al., 1995; Trevisan and Legnani, 1995; Feng et al., 2001; Mu and Wang, 2001;Gao et al.,2003;Mu and Duan,2003;Mu et al.,2007;Ding et al., 2008; Duan and Mu, 2009). In studies of predictability,researchers are more concerned with the predictability of extreme states, like El Ni˜no events, which have signif icant impacts on the variation in climate. Based on climate models,much research has been carried out on the predictability of extreme events.Also,researchers have obtained lots of results on the limited lead times of these extreme events (Luo et al.,2008).However,climate models are imperfect and uncertainties remain in the simulation of atmosphere. So, we cannot obtain the potential backward predictability estimated by climate models. However, few theoretical methods have been used to investigate the backward predictability to date.Therefore, an approach based on the NLLE (Ding and Li,2007; Ding et al., 2008; Li and Ding, 2011b) is introduced here to study the backward predictability of a given state in a chaotic system. If the backward predictability is obtained,this tells us when the specif ic states, especially the extreme states, can be predicted before they happen. It may provide a theoretical reference to the prediction of extreme events in climate modeling.

2. Methods

2.1. NLLE

In an n-dimensional nonlinear dynamical system,the evolution of initial perturbations δ(t0)is governed by

where δ(t)=(δ1(t),δ2(t),...δn(t))Trepresents perturbations at time t, η(xxx(t0),δ(t0),τ)is the nonlinear error propagator that propagates the initial perturbations δ(t0) forward to the perturbation δ(t), and xxx(t) = (x1(t),x2(t),...xn(t))Tis the state vector. τ is integral time.Then,the NLLE is def ined as

where λ(xxx(t0),δ(t0),τ) depends on the initial state xxx(t0) in phase space, the initial perturbations δ(t0), and the integral time τ. The NLLE represents the average nonlinear growth rate of initial errors from t0to t0+τ, which is an advantage over the traditional Lyapunov exponent based on linear error dynamics(Lacarra and Talagrand,1988).The NLLE approach has been widely applied in research into atmospheric and oceanic predictability (Ding and Li, 2009; Ding et al.,2010, 2015; Li and Ding, 2011a, 2013; Zhou et al., 2012;Duan et al.,2013).

2.2. Determination of the forward and backward predictability limits

2.2.1. Forward predictability

If a large number of random initial perturbations with the same magnitude but diあerent directions are superposed on the initial state xxx(t0),the local ensemble mean NLLE can be used to investigate the local average error growth of chaotic systems. Given that a large number of initial perturbations with amplitude ε lie on an n-dimensional spherical surface centered at the initial point xxx(t0),

and the local ensemble mean NLLE of random initial perturbations superposed on the initial state xxx(t0)within a f inite time τ can be given by

where 〈 〉Ndenotes a local ensemble average of samples whose size N is suきciently large(N →∞).The mean LRGIE can be obtained by

For the initial state xxx(t0), ¯E(xxx(t0),τ) increases with time τ and f inally reaches the state of nonlinear stochastic f luctuation, indicating that almost all information from the initial state is lost and the forecast becomes meaningless. The forward predictability limit of the initial state xxx(t0)can then be determined as the time at which the mean LRGIE reaches 95%of the saturation level.As an example,Fig.2 shows the variations of NLLE, ¯λ(xxx(t0),τ) and logarithm of ¯E(xxx(t0),τ)in the Lorenz63 model with initial perturbations δ(t0)=10-5as a function of time τ, where the initial state is xxx(t10000).From Fig.2a, ¯λ(xxx(t0),τ)f luctuates intensely in the initial period. Afterwards,it f luctuates relatively slowly and decreases asymptotically to zero. From Fig.2b,after the zigzag growth process, ¯E(xxx(t0),τ) f inally levels out and enters the nonlinear stochastic f luctuation regime with a saturation value(Fig.2b). According to the def inition, the forward predictability limit of the initial state xxx(t10000)is determined as 14.

2.2.2. Backward predictability

In the backward predictability,the evolution of small perturbations is still governed by Eq. (1) in an n-dimensional nonlinear dynamical system. The time of the given state t0and initial perturbations δ(t0-τ)are known, but the time of the initial state t0-τ is unknown. So, the growth of initial perturbations in backward predictability is expressed by

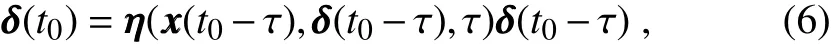
where δ(t0-τ)=(δ1(t0-τ),δ2(t0-τ),...δn(t0-τ))Tis the initial perturbations that are f irst given, η(xxx(t0-τ),δ(t0-τ),τ)is the nonlinear error propagator that propagates the initial perturbations δ(t0-τ) forward to the perturbation δ(t0),xxx(t)=(x1(t),x2(t),...xn(t))Tis the state vector,and τ is integral time. Then, the NLLE in backward predictability is def ined as where λ(xxx(t0-τ),δ(t0-τ),τ)depends on the given state xxx(t0)and the corresponding initial state xxx(t0-τ)in phase space,the initial perturbation δ(t0-τ),and the integral time τ.Similarly,the mean LRGIE in backward predictability can be expressed as:

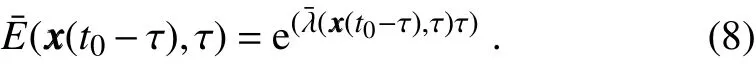
Therefore,to determine the backward predictability of the given state, the corresponding initial state should be found f irst. But then how is the corresponding initial state found?Here, we use the traversing method. That is, we study the growth of initial perturbations by superposing the initial perturbations on previous states before the given state.Once the mean LRGIE reaches saturation at the given state, this previous state is the corresponding initial state.In a continuous time series of an observed dataset (x1,x2,...,xn), xnis the given state and the initial perturbations are δ(t0-τ). Firstly,we superpose the initial perturbations δ(t0-τ) on the previous state xn-1. If the LRGIE reaches saturation at the given state xn, then the state xn-1is the corresponding state being searched for. Otherwise, we superpose the initial perturbations δ(t0-τ)on the previous state xn-2,and conf irm whether the LRGIE reaches saturation at the given state xn. In this way,we can f ind the corresponding initial state.If the state xmis found as the corresponding state,the backward predictability limit of the given state xnis def ined as

For cases of only one corresponding initial state(Fig.3a),it is easy to determine the backward predictability limit of the given state.However,sometimes there may be multiple previous states residing in the same attractor whose LRGIEs reach saturation at the given state. Figure 3b shows that there are three previous states whose LRGIEs all reach the saturation at the given state xn. The terms tm,tkand trare the moments of the three corresponding initial states,respectively,and tnis the moment of the given state. In this case,we always choose a state that maximizes the backward predictability limit of the given state,as the corresponding initial state.So,the previous state xmis the corresponding initial state.Also,the backward predictability limit of the given state xncan be expressed by Eq.(9).

In a limited range of a time series dataset, we use the traversing method to f ind multiple previous states of which mean LRGIEs reach saturation at the given state. Thus, we consider whether there might be more multiple previous states of which LRGIEs reach saturation at the given state if the length of the data is larger. We still take the continuous time series of observed data, (x1,x2,...,xn) as an example. If there are more previous states supplemented into the time series data, the new time series of observed data is (x-n,...,x-1,x0,x1,x2,...,xn). In the original time series data, the previous state xmis the corresponding state. Thus,we choose the state xm-1to superpose the initial perturbations upon. The mean LRGIE reaches saturation before the given state xn. Also, when we choose more previous states before the state xm-1,all the LRGIEs reach saturation before the given state. Therefore,although there are more previous states supplemented into the original time series data,the corresponding initial state does not change, nor does the backward predictability limit of the given state. Taking the same state xxx(t10000)in the Lorenz63 model as an example,the magnitude of the initial perturbation δ(t0)is 10-5.The backward predictability limit of the state xxx(t10000) is about 11, which diあers from its forward predictability limit(about 14).

3. Results

We investigate the forward and backward predictability limit of states in two models formulated by Lorenz. The Lorenz63 model with three variables was designed for the study of atmospheric convection (Lorenz, 1963), while the Lorenz96 model with 40 variables was developed to investigate model problems in data assimilation(Lorenz,1996).

Fig.3. Schematic diagram of the determination of the local backward predictability for (a) only one previous state and (b) multiple previous states. tn is the moment of the given state xxx(tn). tm, tk and tr are the moments of three corresponding initial states xxx(tm),xxx(tk)and xxx(tr),respectively.

Figure 4a shows the variations in the local forward and backward predictability limits of 2000 consecutive states in the Lorenz63 model with the magnitude of the initial perturbations δ(t0)=10-5.From Fig.4a,the variation tendency of the local forward predictability limits is opposite to that of the backward predictability limits for these states. When the forward predictability limits are relatively high (low),the backward predictability limits are relatively low (high).Furthermore,a scatterplot of the forward and backward predictability limits of these states also shows the negative correlation between the forward and backward predictability limits (Fig. 4b). When the forward predictability limits are relatively high,the backward predictability limits are relatively low,and vice versa.Figure 5 shows the spatial distributions of local forward and backward predictability limits of the 2000 consecutive states in the Lorenz63 model. From Fig. 5, we can see that when the forward predictability limit of a state on the attractor is high,its backward predictability limit is always low, on the whole. Also, each butterf ly attractor wing also shows the negative correlation. The correlation coeき-cient of the forward and backward predictability limits for the 2000 consecutive states is-0.35.According to the Student's t-test,the negative correlation between the forward and backward predictability limits is signif icant at the 99%conf idence level. Therefore, there is a negative correlation between the forward and backward predictability limits.

Previous studies have found that the magnitude of initial perturbations has an impact on forward predictability limits.When the magnitude of initial perturbations is large,the forward predictability limits are low,and vice versa.We f ind that the magnitude of initial perturbations has the same impact on backward predictability limits.That is,the backward predictability limits increase as the magnitude of initial perturbations decreases.We take the state xxx(t10000)in the phase space of Lorenz63 and Lorenz96 models as an example. Figure 6 shows the impact of magnitudes of initial perturbations on forward and backward predictability limits of state xxx(t10000)in the Lorenz63 and Lorenz96 models.From Figs.6a and b,the backward predictability limit decreases as the magnitude of initial perturbations increases,which is same as the impact of magnitudes of initial perturbations on forward predictability limits.Therefore,the forward and backward predictability limits decrease as the magnitudes of initial perturbations increase.

Fig.4. (a) Local forward (black) and backward (red) predictability limits of 2000 consecutive states in the Lorenz63 model with initial perturbations δ(t0)=10-5,and(b)a scatterplot of the local forward and backward predictability limits of these states.

Fig.5. Spatial distributions of local (a) forward and (b) backward predictability limits of 2000 consecutive states on the attractor in the Lorenz63 model with the magnitudes of initial perturbations δ(t0)=10-5.

Fig.6.Variation in the two types of local forward(blue)and backward(red)predictability limit with the magnitudes of initial perturbations in the(a)Lorenz63 and(b)Lorenz96 model. σ is the initial perturbations.

Fig.7.Sums of local forward and backward predictability limits of 2000 consecutive states in the(a)Lorenz63 and(b)Lorenz96 model with initial perturbations as 10-2 (blue)and 10-5 (red), and the average values(AV)for six groups in the(c)Lorenz63 and(d)Lorenz96 models with initial perturbations δ(t0)=10-2.

Figures 7a and b show the variations of the sums of local forward and backward predictability limits over 2000 states in the Lorenz63 and Lorenz96 models. It can be seen from Figs. 7a and b that the sums of forward and backward predictability limits of states in two models both f luctuate around a constant value for a f ixed magnitude of initial perturbations.Here, the constant value C is the average value of the sums of forward and backward predictability limits of 2000 states.The average values are diあerent when the magnitudes of initial perturbations are not the same in either model.

To verify whether the average value varies with the number of states in the ideal models,12 000 consecutive states in the Lorenz63 and Lorenz96 models are each equally divided into six groups,respectively.Every group contains 2000 consecutive states.Figures 7c and d show that the average values remain almost unchanged for diあerent groups of states.In the Lorenz system models, the average values of six groups are shown in Table 1,with the magnitude of initial perturbations as 10-2. From Table 1, the average values in every group of either Lorenz system model are almost the same. Also,the average value, 12.4, of the sums of local forward and backward predictability limits of 12 000 states is close to or the same as the average values of every group.It indicates that the average value is constant when the states are suきcient with a f ixed magnitude of initial perturbations.That is,where C is the average value of the sums of local forward and backward predictability limits of suきcient state, and Tfand Tbare the local forward and backward predictability limits of states, respectively. Therefore, the local forward and backward predictability limits are conserved approximately.Also, it is because of the approximate conservation of local forward and backward predictability limits that the forward and backward predictability limits are negatively correlated.

Fig.8.Variation of average values(AV)with the magnitudes of initial perturbations δ(t0)in the(a)Lorenz63 and(b)Lorenz96 model. σ is the initial perturbations.

Table 1.Average values of six groups in the Lorenz63 and Lorenz96 models with the magnitude of initial perturbations as 10-2.

From Figs. 7a and b, when the magnitude of initial perturbations is 10-2in the Lorenz63 and Lorenz96 models,the corresponding average values are 12.5 and 10.6,respectively.When the magnitude of initial perturbations is 10-5,the corresponding average values are also not the same. With the same magnitude of initial perturbations, the average values of the Lorenz96 model are lower. Therefore, for diあerent chaotic systems, the corresponding average values are different, although the magnitudes of initial perturbations are same, indicating that the average value is dependent on the complexity of chaotic systems.A more complex chaotic system has a lower average value.

From Figs. 7a and b, it can also be seen that the average values of either model are larger when the magnitudes of initial perturbations are lower.Also,Fig.8 shows the corresponding average values of diあerent magnitudes of initial perturbations in both models.From Fig.8a,the average values are lower when the magnitudes of initial perturbations are larger.The same situation applies to the Lorenz96 model.Therefore, in a single chaotic system, the average value depends on the magnitude of initial perturbations.The average values decrease as the magnitudes of initial perturbations increase.

4. Conclusions and discussion

In this work, two types of predictability—forward and backward predictability—are proposed, and then the NLLE approach is applied to the Lorenz63 and Lorenz96 models to quantitatively estimate the local forward and backward predictability limits of states. The results show a negative correlation between the forward and backward predictability limits.Also,the local forward and backward predictability limits decrease as the magnitudes of initial perturbations increase.The sums of the local forward and backward predictability limits tend to f luctuate around their average value,which results in the negative correlation between local forward and backward predictability limits. The average value remains constant when states are suきcient.Furthermore,the average value not only depends on the chaotic system, but also the initial perturbations. In a single chaotic system, the average value is larger when the magnitude of initial perturbations is smaller.For diあerent chaotic systems,more complex systems yield lower average values if the magnitudes of the initial perturbations are same.

In future work, we intend to apply the NLLE approach to research into real weather and climate systems,especially extreme weather and climate events. The aim is to obtain the backward predictability of extreme weather and climate events,which may provide a theoretical reference for operational forecasting.

Acknowledgements.This research was jointly supported by the National Natural Science Foundation of China for Excellent Young Scholars (Grant No. 41522502), the National Program on Global Change and Air—Sea Interaction(Grant Nos.GASI-IPOVAI-06 and GASI-IPOVAI-03), and the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(Grant No.2015BAC03B07).