控制城市轨道高架桥梁结构噪声的试验研究

刘兴龙，尹学军，2，孔祥斐，谭 文，刘铁民

（1.隔而固（青岛）振动控制有限公司，山东 青岛266108；2.青岛科而泰环境控制技术有限公司，山东 青岛266101；3.广州地铁集团公司，广州510335）

高架轨道交通具有建设周期短、成本低、运营与维护简单等优点，在许多城市的轨道交通中得到应用。然而，高架轨道交通产生的噪声问题十分突出，在高架轨道交通噪声中，轮轨噪声和高架桥梁结构噪声占主导地位。治理轮轨噪声可以采用钢轨阻尼器技术[1]和声屏障措施；而治理轨道高架桥梁结构噪声主要是采用隔振装置，这包括浮置板和弹性扣件。针对已建成运营的轨道高架桥梁结构噪声问题，应用浮置板技术改造难度很大，而单纯采用弹性扣件改造降噪效果比较有限。在国内，许多科研人员对铁路高架桥梁的结构噪声问题进行了试验与数值模拟研究。在国外，德国的工程技术人员开展应用TMD控制铁路钢结构桥梁噪声的工程试验研究，降噪效果达到了3 dB(A)以上。

广州市轨道交通4 号线的线路全长41.247 公里，其中高架线长30.187公里，地下线长11.06公里。该地铁线路有多个敏感点噪声超标量较大。针对这一问题，本文对该线路高架桥梁的噪声进行测试分析，并应用TMD 技术对桥梁结构噪声进行控制研究。

1 振动噪声测试与模态分析

1.1 振动噪声测试分析

在高架线的噪声敏感点选取了一跨30 m 长混凝土简支箱梁高架桥进行了过车振动与噪声测试，桥梁断面结构与振动噪声测点布置如图1所示。振动与噪声测点位于同一断面的桥梁跨中位置，振动测点包括钢轨、轨道板、桥面和箱梁底部，噪声测点包括桥下1.5 m 处、与桥面等高且距中心线一侧的7.5 m和15 m处。测试时地铁行车速度为45 km/h。

图1 桥梁结构与测点布置示意图

测试结果如图2至图9所示。

图2 钢轨垂向振动加速度时程

图3 钢轨振动加速度功率谱

从图3可以看出，钢轨振动峰值频率集中在500 Hz与550 Hz，轨道板振动能量主要集中在80 Hz，在70 Hz 和84 Hz 峰值也比较明显。桥面翼缘振动峰值比较分散，主要位于92 Hz、95 Hz和105 Hz，在56 Hz、60 Hz和70 Hz以及230 Hz～270 Hz频率范围的峰值略显突出。桥面中间与桥梁底部振动频谱非常一致，峰值主要位于82 Hz、95 Hz和102 Hz。桥下噪声能量分布则非常集中，分别位于68 Hz、78 Hz和90 Hz，在90 Hz峰值最突出。

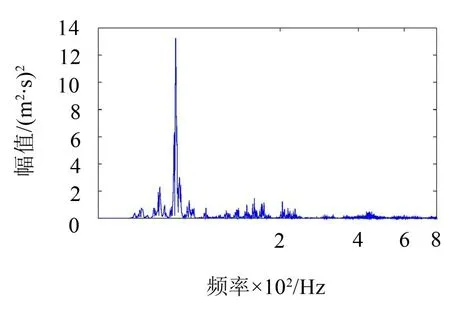
图4 道床垂向振动加速度功率谱

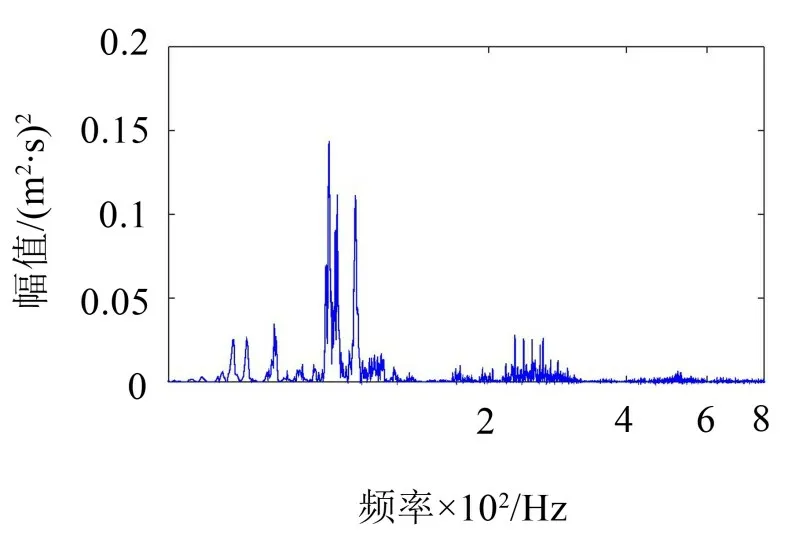
图5 桥面边缘垂向振动加速度功率谱

图6 桥面中间垂向振动加速度功率谱

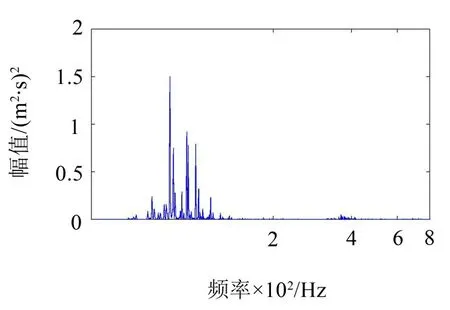
图7 桥面底部垂向振动加速度功率谱

测试结果表明，列车经过时引起桥梁共振，共振频率主要位于80 Hz～90 Hz 及其附近，并随桥梁位置略有变化，高架桥噪声是由桥梁共振辐射产生。从图9 中不同测点噪声A 计权声压级频谱可知，与桥梁距离越远，80 Hz频带噪声峰值越低。

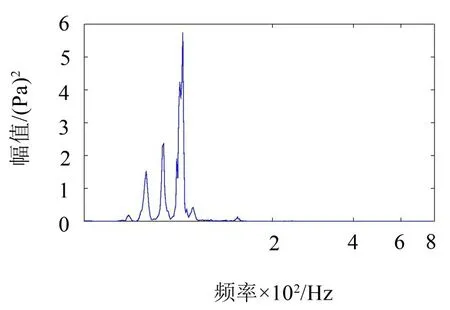
图8 桥下噪声功率谱

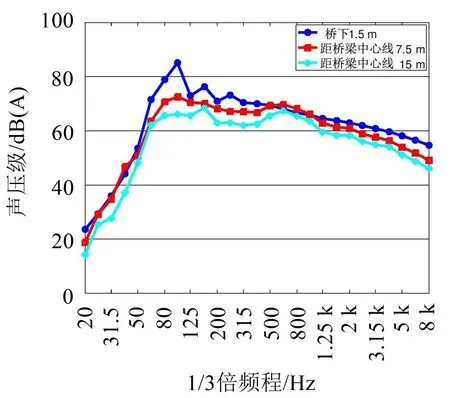
图9 不同测点噪声A计权声压级频谱对比

但是，在7.5 m 和15 m 测点的噪声声压级值在625 Hz 频带略显突出，这一峰值频带与钢轨垂向振动峰值频率一致，可以确定这两处测点在该频带噪声属于轮轨噪声。由于桥下噪声测点共振噪声最突出，而且受桥面轮轨噪声影响较小，最能代表高架桥梁的结构噪声特性，因此降噪效果的对比与评价针对桥下1.5 m处噪声进行。

1.2 模态分析

利用ANSYS 有限元软件对高架桥梁进行模态分析，建模时采用Solid185 单元将桥梁与轨道板离散，利用beam185 单元模拟钢轨，利用combin17 单元模拟扣件。主梁的混凝土型号为C50，弹性模量为2.4×104 MPa，泊松比为0.2，扣件刚度为60 kN/mm。为了验证模态计算结果，对桥梁的垂向振动模态进行试验测试，表1 所示为桥梁低阶垂向弯曲模态测试结果与有限元模态分析结果对比。

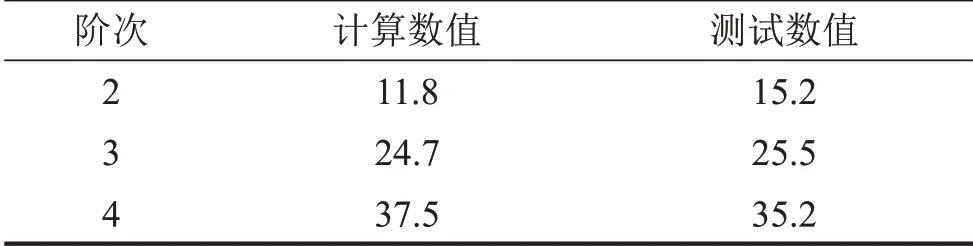
表1 垂向弯曲模态分析结果对比/Hz

图10 为第2 阶试验模态与计算模态的振型对比，图11为高阶模态振型对比。

图10 第2阶模态振形对比

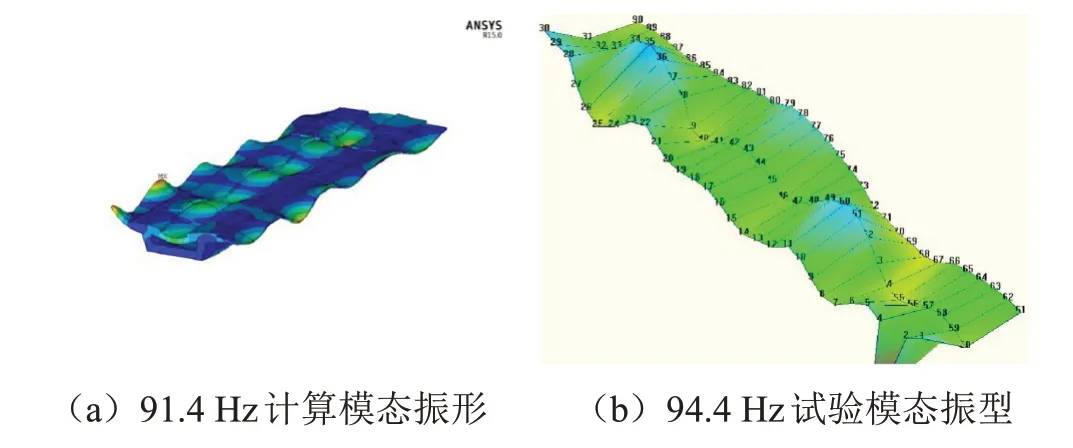
图11 高阶模态振型对比

低阶模态计算结果与试验测试结果比较一致，但随频率增高，模态越来越密集，各模态振型不再表现为结构整体变形，试验模态测试难以准确获得高阶模态的频率、振型，计算模态和试验模态很难对应起来，因此接下来利用有限元分析桥梁的高阶模态。有限元模态分析结果显示，54.5 Hz以上桥梁模态表现为桥梁不同部位的各自振型，主要是桥梁翼板、箱梁盖板和箱梁底板三部分。从图11 可以看出桥梁翼板、箱梁盖板和箱梁底板振型不再保持一致，而表现为桥梁局部模态振型。

2 TMD振动控制理论与应用

2.1 TMD 控制设计理论与方法

目前应用TMD 对单自由度振动系统进行振动控制设计的理论与方法已很成熟，因此本文对单自由度系统TMD 振动控制理论与设计方法进行简要介绍。假设主系统的刚度为K，质量为M，TMD的刚度为k,，质量为m，则主系统的固有角频率为Ωn=固有角频率为质量比为μ=m/M，固有角频率比为γ=ωn/Ωn，可以得到满足最优同调条件TMD与主振动系统的固有频率比

同样可得到最优阻尼比为

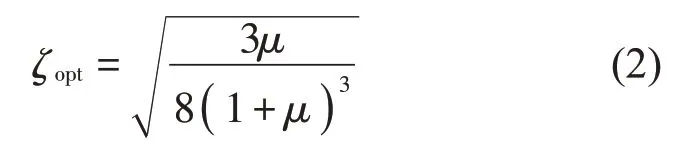
利用式(1)至式(2)即可对单自由度系统的TMD进行设计，近年来一些研究学者提出了应用TMD控制多自由度系统的设计方法。这种设计方法通过模态分析将多自由度振动系统解耦转换为模态空间中多个非耦合单自由度振动系统，然后利用等价质量识别法将过模态质量转化为具有物理意义的等价质量。设N 自由度系统的第i 阶模态振形向量为把i阶模态的固有向量在第j点的值定义为1，对固有向量进行正规化，则第j 个自由度在第i阶模态中的等价质量可以表示为

最后利用单自由度系统TMD 设计理论对多自由系统中需要控制的模态进行TMD设计，等价质量识别方法的详细介绍可参考文献[6]。

根据式（3）所示计算方法可得到高架桥每阶垂向弯曲模态的等价质量，在60 Hz～100 Hz频率范围的模态频率与等价质量结果如图12所示。

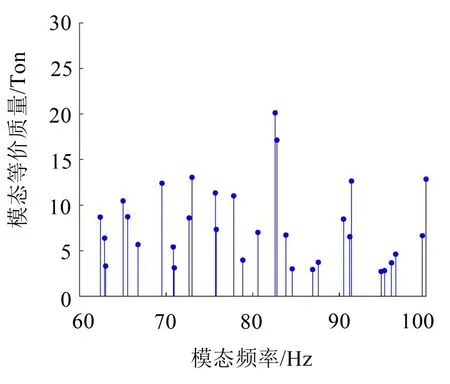
图12 高架桥模态频率与质量

从图中可以发现，在这一频率范围，模态分布非常密集，过车时桥梁振动频率范围集中在80 Hz～90 Hz，由此可知过车激励引起的主要振动模态位于82.6 Hz、82.8 Hz和91.4 Hz，其等价质量分别为20.13吨、17.13 吨和12.64 吨。本文针对这三种模态的振动控制进行TMD设计。根据多自由度系统TMD设计方法，并考虑TMD 设计安装尺寸及桥梁承重能力，首先确定TMD质量，然后根据TMD的理论最优频率与阻尼比进行弹簧和阻尼设计，TMD安装位置位于3阶模态振型的波腹处。

传统的螺旋钢弹簧难以实现频率位于80 Hz～90 Hz 的TMD 设计要求，因此，本文提出了将固定-固定梁作为弹簧元件，质量元件设置在梁中间的TMD结构，其示意图如图13所示。

通过改变梁的长度和截面尺寸调整TMD频率，TMD 通过螺栓与桥梁固定。根据上述三种控制模态振型，在连续3 跨30 m 简支式轨道高架桥梁安装了TMD，图14 为箱梁内TMD 安装后现场照片。在桥梁两侧翼缘各布置了24 个50 kg 的TMD；沿桥面中心线布置了20个100 kg的TMD；在箱梁内沿底板中心线布置了24个100 kg的TMD。

图13 TMD结构示意图

图14 箱梁内底板TMD安装现场照片

2.2 结构噪声控制效果

在连续3 跨桥梁安装TMD 后，按照图1 所示的噪声测点布置方式，在安装TMD桥梁的中间一跨与连续3 跨未安装TMD 的中间一跨高架桥进行了过车噪声对比测试。取10组测试数据进行对比，TMD安装段和未安装段噪声对比如表2所示。

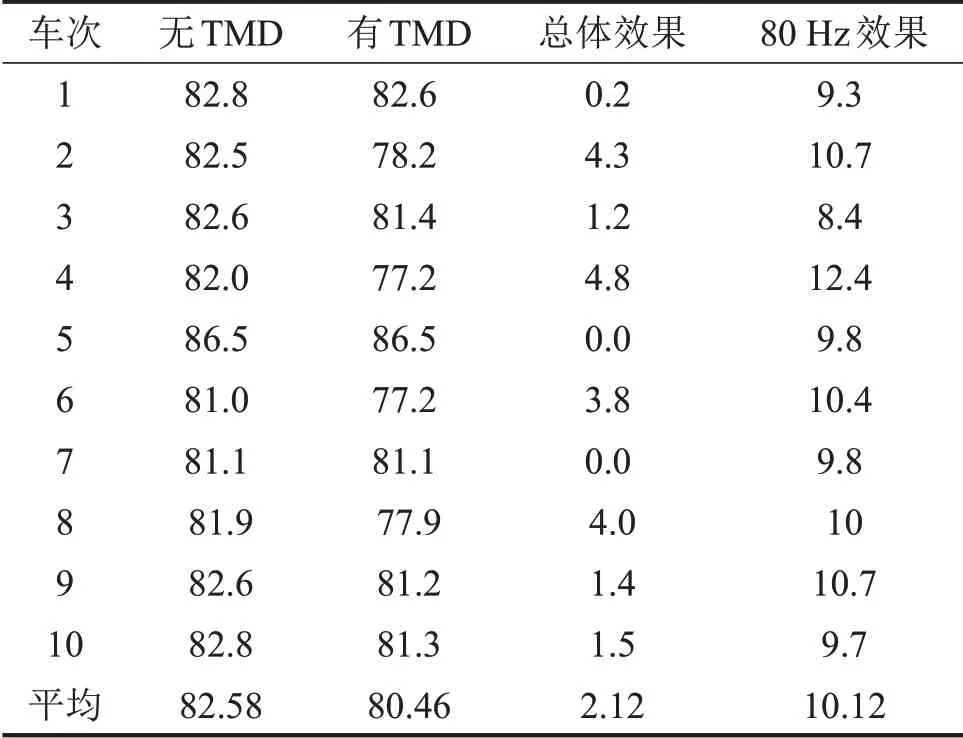
表2 降噪效果对比/dB(A)

除第5 次过车噪声声压级较高以外，10 次过车TMD未安装段桥下噪声水平大部分在81.0 dB(A)～82.8 dB(A)。相较于未安装TMD 的高架桥梁噪声，安装TMD的高架桥下噪声水平差别较大，10次过车的降噪效果可以分3种情况：

（1）第1次、第5次和第7次降噪效果不明显；

（2）第3次、第9次和第10次降噪效果一般；

（3）第2次、第4次、第6次和第8次降噪效果非常好。

虽然降噪效果存在差别，但是TMD控制频带在80 Hz 降噪效果明显且一致，达到了9.3 dB(A)～12.4 dB(A)。

通过分析10次过车声压级频谱发现存在2种典型的噪声对比结果，这里给出了第4次和第5次过车时2组噪声对比结果，分别如图15至图16所示。

图15 第4次过车时噪声A计权声压级对比

图16 第5次过车时噪声A计权声压级对比

第4次过车时未安装TMD段的桥下噪声存在2处峰值，为80 Hz 和500 Hz，安装TMD 的高架桥下噪声频率在63 Hz～250 Hz和500 Hz以上的频带声压值均明显降低。在80Hz 和500 Hz 频带声压值分别降低12.4 dB(A)和13.8 dB(A)。第5次过车时未安装TMD 段的桥下噪声只在80 Hz 频带存在峰值，安装TMD 段的高架桥下噪声频率在63 Hz～80 Hz 和1 000 Hz 以上频带范围声压值降低，但在125 Hz～400 Hz 频带声压级反而升高，这是降噪效果差别的根源所在。广州地铁4 号线振动噪声测试对比表明，桥下噪声测点上、下行降噪效果存在一定差别，上行线降噪效果为3.12 dB(A)，下行线降噪效果为2.83 dB(A)[7]。这种差别主要是由上、下行列车经过测点位置速度不同产生的。

3 结语

(1)广州地铁4 号线简支式30 m 跨箱梁高架桥梁过车噪声超标是由高架桥梁共振辐射噪声引起，振动噪声主要频率范围位于60 Hz～100 Hz，峰值频率主要位于80 Hz 和90 Hz。在这一频率范围内桥梁共振模态表现为桥梁各部件局部振动。

(2)研发设计了高频梁式TMD 结构，应用多自由度TMD 控制理论在3 跨30 m 轨道高架桥安装了控制多阶模态的TMD。

(3) 噪声测试结果表明，TMD 控制频带降噪效果明确且稳定，达到9.3 dB(A)～12.4 dB(A)。高架桥下1.5 m 处测点总体降效果最大能达到4.8 dB(A)，10 次过车平均降噪效果为2.1 dB(A)，但多次过车时降噪效果差别较大，这主要是由于上、下行列车经过测点速度不同导致降噪效果产生差异。