浅议共轭薛定谔方程及其物理量算符

魏 标，廖荣宝，金 凤，金晓艳，田志美，董秋静，陈水生，刘 杰，马成丙

（阜阳师范学院 化学与材料工程学院，安徽 阜阳 236037）

量子力学对现代科技产生了巨大影响，半导体技术[1]、晶体管[2-3]、原子钟[4-6]、激光技术[7-8]、核武器[9-10]、量子通信技术[11-14]、电子存储设备的巨磁阻效应[15-18]等都与量子力学理论相关。而且量子力学理论还将持续推动人类对自然界的认识。

1925年，奥地利物理学家薛定谔采用描述波动力学的波函数描述电子的运动，标志着描述微观粒子的波动力学正式诞生[19-21]。1926年，德国物理学家Born给出了波函数物理意义的解释，即薛定谔方程得出的波函数的模平方是概率密度分布函数[22]。体系的状态函数可通过求解薛定谔方程获得，采用可观测物理量对应的算符作用于状态函数可获得体系的各种物理性质。

状态函数一般是复函数，状态函数的模平方是个实函数，且对于任何一个空间位点，模平方函数取值均为正。波恩把模平方函数与概率密度对应起来，因此模平方函数具有明确的物理意义。不同于模平方函数，波函数本身及其共轭函数的物理意义并不明确。对波函数本身及其共轭函数物理意义的研究依然很有必要。本文对比了薛定谔方程及其共轭方程的数学形式差异，讨论了二者本征函数、物理量算符之间的关系。

1 共轭薛定谔方程及算符

1.1 共轭薛定谔方程的推导

含时薛定谔方程如(1)式所示。对(1)式两边同时取复数共轭可得(2)式。采用(3)式把波函数ψ(r,t)的复共轭函数定义为一个新的波函数φ(r,t)，则必有(4)式成立。现把(4)式命名为共轭薛定谔方程。显然，如果存在状态函数服从薛定谔方程(1)，那么必有与其共轭的状态函数服从薛定谔方程(4)。反过来，如果通过共轭薛定谔方程获得一个状态函数φ(r,t)，那么φ(r,t)的复共轭函数必服从薛定谔方程(1)。

依据Born的观点，状态函数与其共轭函数的乘积对应于概率密度。记服从薛定谔方程(1)的状态函数ψ(r,t)对应的概率密度为ρψ(r,t)，则有(5)式关系。记服从共轭薛定谔方程(4)的状态函数φ(r,t)对应的概率密度为ρφ(r,t)，则有(6)式关系。此时，有(7)式成立。依据密度泛函理论，具有相同密度分布的体系有相同的物理性质。因此态函数ψ(r,t)与其共轭函数φ(r,t)在描述物理性质方面并无本质差别。所以，按照(4)式的共轭波动方程，也可解得态函数。依据密度泛函的观点，这个态函数也可用于描述体系的物理状态和各种物理性质。

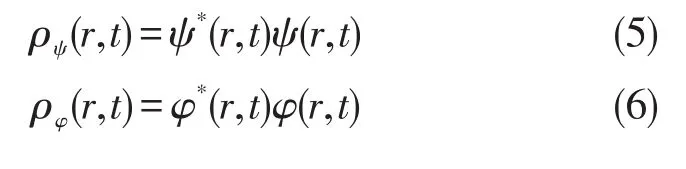
1.2 共轭薛定谔方程的算符

依据量子力学理论，可观测物理量都对应一个线性厄密的算符。薛定谔方程(1)中各个物理量对应的算符是已知的。但适用于薛定谔方程(1)的算符不一定适用于共轭薛定谔方程(4)。由于方程(4)与方程(1)是共轭关系，且两方程的解也有对应的共轭关系，因此适用于共轭薛定谔方程(4)的算符与适用于薛定谔方程(1)的算符间也有共轭关系。现分别给出适用于共轭薛定谔方程(4)的能量算符、哈密顿算符、动量算符、角动量算符，见(8)式至(11)式。

2 含时波函数必是非实数波函数

把(1)式和(4)式相减可得(12)式。假设含时波函数是实数波函数，则必有关系(13)式成立，进而有(14)式成立。综合(12)式和(14)式可知，状态ψ(r,t)和φ(r,t)不存在。若含时波函数是非实数波函数，则无此问题。因此，由含时波动方程(1)或含时波动方程(4)获得的波函数必是非实数函数。

3 小结

本文通过对薛定谔方程的变换得到了共轭薛定谔方程。给出了共轭薛定谔方程的某些物理量对应的算符。通过共轭薛定谔方程也可解得体系的状态函数，且共轭薛定谔方程解得的波函数对应的概率密度分布与原薛定谔方程解得的波函数对应的概率密度分布完全相同。因此得出，共轭薛定谔方程与原薛定谔方程具有同等地位。并进一步通过对原薛定谔方程和共轭薛定谔方程的对比得出含时波函数必是一个非实数函数。