宽视场成像网格化算法中w-plane最优经验值研究*
2019-04-19于晓雨卫守林石聪明
于晓雨,邓 辉,2,梅 盈,卫守林,石聪明,王 威,戴 伟,王 锋,2
(1. 昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500; 2. 广州大学天体物理中心/物理与电子工程学院,广东 广州 510006;3. 中国科学院国家天文台,北京 100101)
平方千米阵列(Square Kilometer Array, SKA)是目前国际上建造的最大综合孔径射电望远镜[1],它由数千个反射面天线和多达一百万个低频天线组成,总接收面积达到一平方千米。
平方千米阵列科学数据处理(Science Data Processor, SDP)是望远镜设计中的一个重要组成部分。科学数据处理专注于设计硬件平台、软件和算法处理射电望远镜的观测数据[2]。科学数据处理的设计面临的挑战是多方面的,需要处理来自望远镜的海量观测数据。SKA-1(约占10%的总体规模)数据量将达到300 PB/年。为了满足平方千米阵列科学研究开展的需要,科学数据处理在数据处理管线设计中,需要充分考虑数据处理的性能与质量。由于科学数据处理需要的计算力高出现有最大的天文数据处理系统两个数量级,数据处理关键算法的运行速率要达到百万兆级的运算水平。SKA-2的计算力需求估计达到4 exaFLOPS的水平。因此,开展对科学数据处理中关键算法的研究,提高数据处理的性能具有显著的意义。
网格化(Gridding)算法是综合孔径望远镜数据处理中的一种重要算法,对计算的消耗占据了很大比重。对网格化算法进行性能优化,对科学数据处理有显著的价值和意义。低频射电望远镜大视场成像受到很多条件的制约,其中最重要的一个影响因素是非共面基线效应。在大视场与非共面基线效应下,对可见度数据直接进行傅里叶变换会导致图像严重畸变,因此,在大视场成图时,解决w项的问题至关重要。目前,应对大视场与非共面基线效应的算法有:faceting[3],三维傅里叶变换[4],w-projection[5],w-stacking[6]和warped snapshots[4]等算法以及其他复合算法。在这些方法中,w-projection和w-stacking是目前应用相对较广的网格化算法。其中,w-projection算法在牺牲较大内存的情况下,具有优越的计算速度和误差控制。该方法不仅可以使用传统的洁化方法去卷积,还可以选择多尺度洁化方法,在高动态范围下,有较大的优势,相位中心基本不失真。w-stacking算法在图像空间以消耗更多的内存为代价处理傅里叶空间中w项,计算速度优于w-projection[7]。
在w-projection和w-stacking算法的具体实现过程中,w-plane是一个重要参数。在w的最大值和最小值之间分出多个w-plane,对不同w-plane的可见度数据使用不同的卷积核进行卷积运算。因此,w-plane的数量直接影响算法的计算速度、内存开销以及成图质量。本文主要对w-projection和w-stacking算法在实现与实际运行中的w-plane进行实验研究,利用SKA-1低频阵台站数据和澳大利亚SKA探路者(Australian SKA Pathfinder, ASKAP)软件包进行模拟观测,以期掌握w-plane对整体计算性能的影响,为后期的平方千米阵列科学数据处理建设以及国内科学数据中心建设中的管线系统设计提供参考。
1 w-plane
低频射电望远镜大视场成像最重要的一个影响因素是非共面基线效应,在非共面基线效应的影响下,w的值远大于1,因此直接对可见度数据进行二维傅里叶变换的条件已经不满足,针对这一问题,天文学家提出了一系列算法用来应对非共面基线效应造成的图像畸变。w-projection算法通过将不同w值的可见度数据投影到w=0的平面,从而消除w项的影响,有效提高成图质量。w-stacking算法能够在像平面矫正非共面基线效应引起的相位偏移,从而有效还原天空亮度分布。
在射电综合孔径成像处理过程中,可见度数据与天空亮度之间的关系:
(1)
w-projection算法将不同w值的可见度数据投影到w=0的平面,(1)式简化为
(2)
经过简单的指数运算,(1)式变为(3)式和(4)式:
(3)
(4)
(3)式、(4)式可以改写为(5)式,其中卷积核通过(6)式近似计算得到:
V(u,v,w)=G^(u,v,w)*V(u,v,w=0),
(5)
(6)
以上各式中,V(u,v,w)是w非零的可见度数据;I(l,m)表示天空亮度分布;V(u,v,w=0)表示
w=0的可见度数据;G(l,m,n)表示w项;G^(l,m,n)表示卷积核。
上述过程显示,在w-projection算法中,卷积核是算法的核心。理想情况下,位于不同w-plane的可见度数据,在计算过程中应该采用不同的卷积核。在实际计算过程中,一般计算w的最大和最小值,在最大和最小值之间平均分成多个w-plane,然后对每个w-plane按照(6)式计算卷积核并保存,最后对每个可见度数据与其距离最近的w-plane的卷积核进行卷积,从而实现到w=0平面的投影。
显而易见,w-plane的值越大,投影效果越好,但是计算量和内存消耗大;w-plane的值越小,计算量和内存消耗小,但是投影效果欠佳。当w-plane的数量为0,则直接退化为二维傅里叶变换。文[5]在前期研究中取最大的w值的平方根作为经验值。
2 w-stacking 算法中w-plane
w-stacking算法的提出是为了消除非共面基线效应对大视场成像的影响,但是不同于w-projection算法,w-stacking算法并没有消除w项,而是对其进行了修正。
根据(1)式将uv空间转换到lm空间得到(7)式:
(7)
对(7)式两边在w范围内进行积分得到(8)式:
(8)
其中,wmax和wmin分别为w的最大值和最小值。(8)式等号右侧包括两部分:(1)二维傅里叶变换;(2)对w的复数积分。对(8)式等号右侧离散化得到(9)式:
(9)
w-stacking算法的实现步骤如下:
(1)根据可见度数据w的范围设定w-plane的细分粒度;
(2)依据每个可见度数据的w值,将可见度数据网格化到某一w-plane;
(3)对每个w-plane的可见度数据进行二维傅里叶变换得到相应图像;
(4)根据w值对各个w-plane的图像进行相位矫正;
(5)加权叠加所有图像,得到最终图像。
在w-stacking算法实现过程中,w-plane分的过粗导致产生伪影,分的过细又增大计算量和内存消耗。同时,w-stacking算法将不同w-plane上的可见度数据看成是相互独立的,各个面的数据可以并行进行二维傅里叶变换和相位改正,因此,w-stacking算法在并行实现方面具有优势。
3 观测模拟仿真实验
3.1 实验环境
为了验证w-plane的影响,获得较为理想的w-plane值,在确保成像质量的情况下降低成像处理时间,本文进行了一系列实验。数据处理软件采用澳大利亚SKA探路者的数据处理软件系统[8]。澳大利亚SKA探路者通过名为ASKAPsoft的软件系统进行望远镜观测控制和数据处理[9],ASKAPsoft框架由3部分组成:望远镜观测系统、处理中心和科学数据存档。澳大利亚SKA探路者通过bash shell脚本组合ASKAPsoft中的程序形成数据处理管线,主要的数据处理管线有数据摄取管线、定标管线和成图管线[10]。
本实验在8台汉柏服务器上完成,具体硬件配置如表1。
3.2 模拟观测与成像处理
为了分析w-plane对w-projection算法和w-stacking算法的影响,采用模拟观测、成像、对后续图像进行分析的方法验证不同的w-plane造成的影响。

表1 硬件设备参数Table 1 The parameters of device
3.2.1 模拟观测
实验采用SKA1-Low望远镜的512个天线台站坐标数据,天线布局如图1。天空模型由73个点源构成,整体形状为 “米” 字,如图2(a)。实验采用16个计算节点,每个计算节点处理一个通道的数据,通道带宽1 MHz,因此观测频率覆盖范围16 MHz,积分时间间隔150 s,模拟观测时长6 h。SKA1-Low天线频率覆盖范围50~350 MHz,本实验中心参考频率为100 MHz,设置16个带宽为1 MHz的通道,因此观测频率范围为92~108 MHz。
使用模拟观测程序对天空模型进行16个通道的模拟观测,得到18 837 504行5.5 GB的模拟可见度数据。
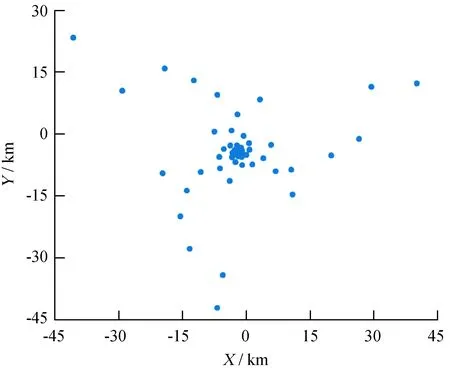
图1 天线分布
Fig.1 Antennas layout
3.2.2 成像处理
使用w-projection算法和w-stacking算法,对模拟观测获得的可见度数据16个通道进行连续谱成图。ASKAP成图管线在8个计算节点上并行运算,每个计算节点处理两个通道。实验过程中不断改变w-plane的数量,得到不同w-plane设置下的图像,并记录每次成图时间供后续分析使用。
图2(b)是二维傅里叶处理得到的图像,可以看到w项影响导致的拖尾效应(Smearing)非常明显。图3是w-plane数量设置为171的情况下,w-projection算法和w-stacking算法处理得到的图像,拖尾效应得到抑制,但边缘的模拟星并没有被很好地还原。
3.2.3 图像质量评价方法
为了评价不同w-plane数量下的两种算法的成像质量,研究采用了SELAVY软件包,该软件包是Duchamp星源搜索算法在ASKAP软件中的实现模块,用来搜索观测结果中的星数量。由于在仿真观测时已经预设了总的星数为73,同时所有星的位置已知。因此,通过SELAVY搜索出的星与已知天空模型星进行对比,利用正确还原的星数量来快速判断成像的质量。图4(a)显示了随着w-plane数量的增长,两种算法处理时间的变化。图4(b)显示了随着w-plane数量的增长,SELAVY搜索出点源数量的变化。
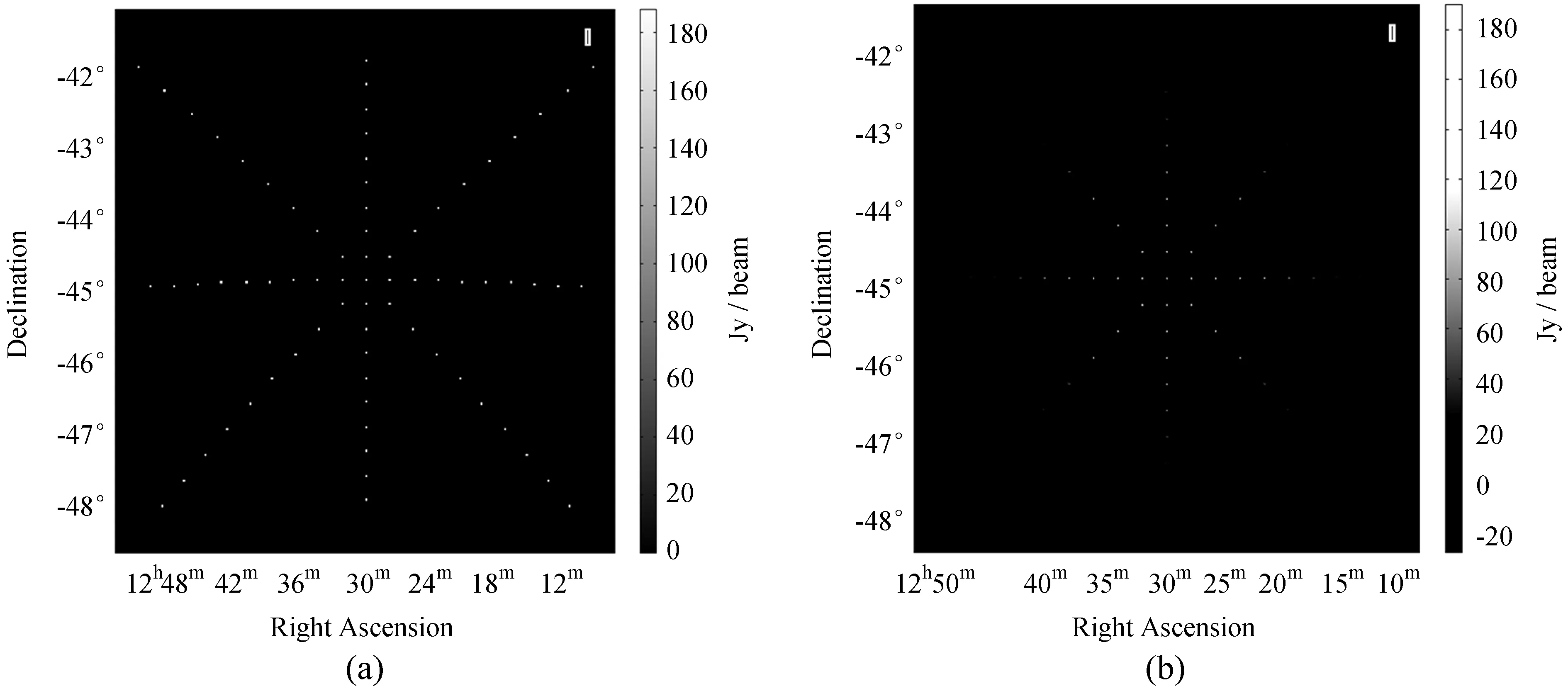
图2(a) 天空模型图; (b) 二维傅里叶变换成像结果
Fig.2(a) Sky model image; (b) The result of two-dimensional Fourier transform imaging
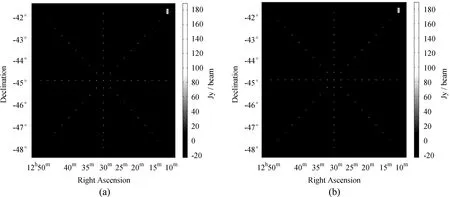
图3(a) w-projection算法的成图结果; (b) w-stacking算法的成图结果
Fig.3(a) The result of the w-projection imaging; (b) The result of the w-stack imaging
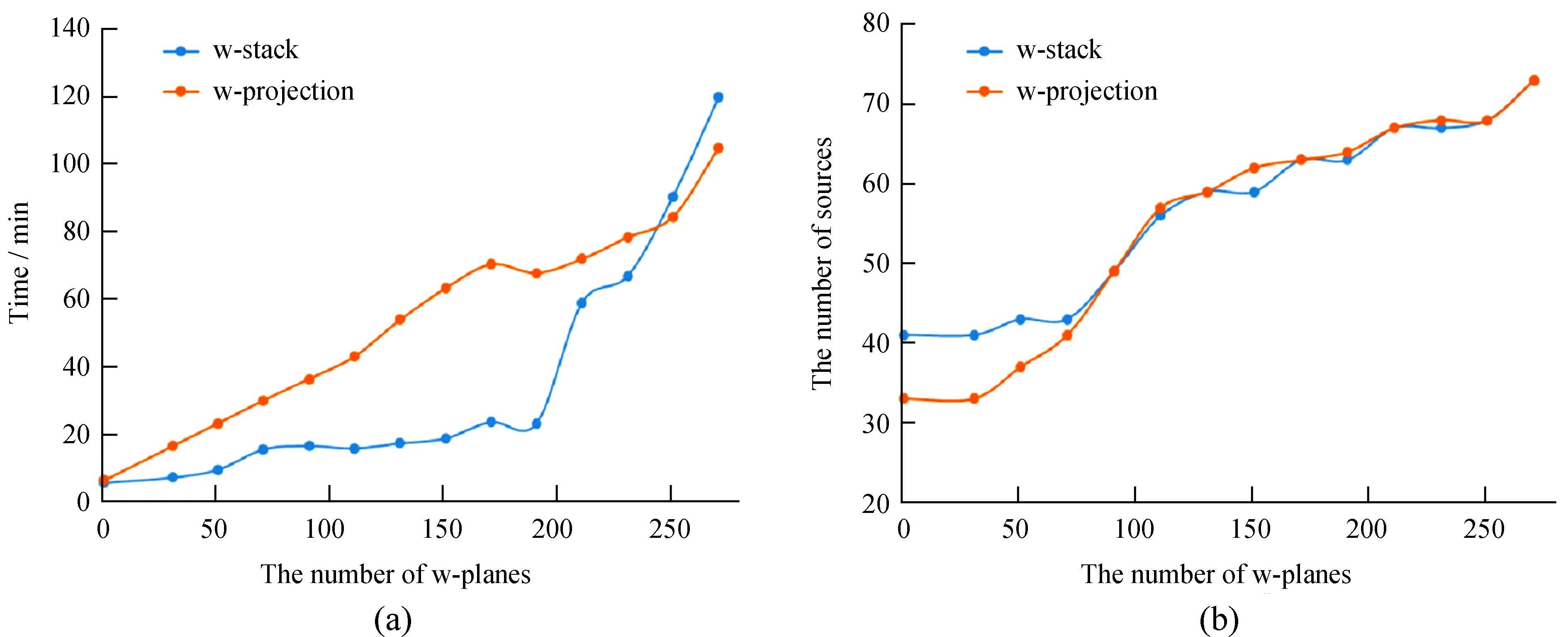
图4(a) 计算时间与w-plane的关系; (b) SELAVY搜索出点源数量与w-plane的关系
Fig.4(a) The relation between the running time and w-plane;(b) The relation between the number of searched sources and w-plane
4 结果分析
本实验最大基线长度81 602 m,最大w约为28 000个波长。根据文[5]研究的结果,w-plane值一般设置为最大w的平方根,也就是167。
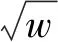
SELAVY软件包对两种算法在不同的w-plane时成图结果进行星像统计。从图4(b)可以看到在w-plane较小的情况下,w-stacking算法成图得到星的数量多于w-projection算法的结果,但是随着w-plane的增加两者的成图质量近似相同。
5 结 论
综上所述,针对w-projection算法和w-stacking算法在管线中的应用,有如下结论:
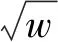
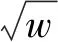
本文的工作表明,平方千米阵列数据处理管线应根据不同的需求选择不同的网格化算法,后续工作以提高运算速度、提高算法的并行性为研究重点,以获得更好的处理能力。
