耀变体在射电波段的偏振研究*
2019-04-19徐小林张皓晶易庭丰任国伟李富婷吴月承
徐小林,张皓晶,易庭丰,张 燕,余 莲,任国伟,李富婷,吴月承,张 雄
(云南师范大学物理与电子信息学院,云南 昆明 650500)
耀变体作为活动星系核的一个子类,辐射与观察者的视线相一致的耀变体(Blazars)被相对论喷流
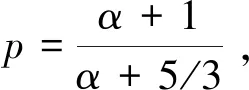
由于法拉第散射,去偏振对同步辐射源的偏振度有一定的作用。偏振的形式可以表示为p∝e-λ4,其中λ为观测波长[3]。法拉第旋转量(RM)可能与磁场拓扑结构有关[4-5],并存在一种特殊的磁场扭曲效应[6-7]。另外,在近期的研究中,文[8]提出了法拉第旋转量中的湍流特性,推导出了一种p∝e-4/ζ的形式,其中ζ与湍流能级联的指数有关。一些模拟也表明,湍流可能是耀变体偏振变化的一个原因[8]。近年来,综合利用统计相关函数研究了三维各向异性磁流体动力学,说明湍流对偏振随波长变化的影响,也表明可以应用Lazarian & Pogosyan(2016)给出的磁流体动力学湍流建模结果分析UMRAO数据库的射电波段的偏振。
本文研究射电波段中的去偏振特性,揭示偏振随波长变化的物理原因。收集了UMRAO数据库中2009年9月到2012年5月的偏振数据,通过p∝aλ-b的幂律拟合多波段偏振度,其中b为拟合参数。就耀变体而言,首先验证Lazarian & Pogosyan给出的法拉第旋转的物理条件,然后给出与波长有关的去偏振特征的物理原因。
1 样本选择和拟合结果
一般认为,耀变体的偏振是由相对论电子同步辐射产生的,有单电子同步辐射和集体电子同步辐射之分。由于耀变体的偏振是由大量电子产生的,所以用集体电子同步辐射研究耀变体的偏振和去偏振。
由集体电子同步辐射,电子的谱发射率[9]为
(1)

(2)
若频率满足ν(γ1)≪ν≪ν(γ2),则集体电子同步辐射的偏振度为
(3)
耀变体的连续谱通常满足Fν∝ν-α,α为谱指数,n和α的关系为n=2α+ 1。因此耀变体的偏振度可表示为[2]
(4)
由此可以看出,耀变体的偏振度与频率(波长)无关。
以上只针对均匀辐射源,而耀变体一般是非均匀辐射源。文[10]提出了一种估算不均匀源的偏振,表达式为
(5)
其中,Π(ν)为磁场有序度,由磁场的几何性质决定。由(5)式可以看出,偏振度与频率(波长)有关,偏振度随波长变化而变化。
产生波长相关偏振(Wavelength Dependence Polarization, WDP)的原因,即产生Π(ν)的原因,解释有多种,磁场湍流会对偏振产生一定的影响(去偏振的内部原因)。产生波长相关偏振的原因有2种:(1)热辐射和同步辐射混合作用产生波长相关偏振;(2)同步辐射中本来就存在波长相关偏振[11]。耀变体的谱指数α一般在0~2,对应于(4)式的偏振度为60%~82%。然而实际测得的射电波段的偏振度一般低于10%,则Π(ν)起主要作用。
文[12]分别讨论了法拉第旋转主导和湍流主导下对偏振的影响,偏振随波长的变化:(1)在法拉第旋转主导下,偏振随波长变化的关系为p(λ)∝λ-1/2或者p(λ)∝λ(-1-m)/2;(2)在湍流主导下,偏振随波长的变化关系为p(λ)∝λ(-1+m)/2或者p(λ)∝λ(-1-m)/(2-mφ),其中m,mφ分别对应湍流的能谱指数和法拉第旋转量的能谱指数,偏振随波长变化的关系服从幂率形式。在文[13]中用p=aλ-b拟合数据,采用此形式拟合UMRAO数据库中的射电数据,得到不同源对应的b值,再得到与之相对应的m值。
如果假定mφ=0,则湍流主导与法拉第旋转主导下的偏振随波长变化保持一致,p(λ)∝λ(-1-m)/2;mφ> 1的效果与mφ=1的效果一致,则取mφ=1[12]。
在选取样本时,由于不同探测器之间的不协调性,只选取了UMRAO数据库的4.8 GHz、8 GHz、14.5 GHz偏振数据,且只选了2009年9月到2012年5月的偏振数据。在众多活动星系核(Active Galactic Nuclei, AGN)中,只选取利于研究的22个耀变体源。在选取的22个耀变体源的数据中,观测的平均周期为1天,且2009年9月到2012年5月没有表现出激烈的爆发。由于3个波段的偏振数据不是准同时性的,为了研究的方便,对它们的偏振和误差分别求平均值,得到3个数据点。在进行幂率拟合时,3个数据点足以说明幂率情况,拟合具有可行性。UMRAO数据库的数据来源于北方扩展毫米阵列(NOrthern Extended Millimeter Array, NOEMA)射电望远镜观测的数据,其主要目的是用于校准其他射电望远镜获得的数据,其中的线偏振为部分线偏振,数据库仅包含每日观测偏振度P的误差保持在3σ以内。
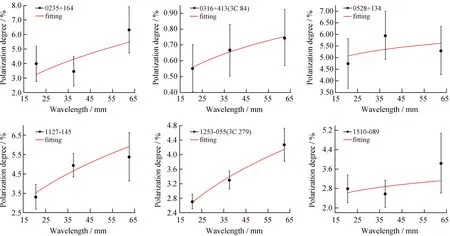
图1b< 0时的耀变体幂率拟合情况,横轴为波长,纵轴为偏振度
Fig.1 Fitting power factor of blazars source forb< 0, where the horizontal axis is the wavelength and the vertical axis is the polarization degree
由图1可以看出,b< 0,偏振度随波长的变长而降低,dp/dλ> 0,表现出反常去偏振。很难用磁流体动力学湍流和法拉第旋转简单地解释产生dp/dλ> 0的物理机制。反常的去偏振特性,即偏振随波长变长而增加,在文[13]中,光学波段表现得很少,而本文的射电波段有相对较多的表现,大约占耀变体源的27%,接近1/3。这种现象意味着大约有1/3的耀变体喷流中,吸积盘内部的偏振比外围的偏振低,相当于外围磁场强,越靠内磁场越弱,这是很反常的。这种反常说明很有可能这1/3耀变体的吸积盘或喷流中的磁场发生了扭曲,这种扭曲使得常规的同步辐射和磁流体动力学模型中的磁场在数据结果中与预测的不一致,究其原因认为,有可能是湍动磁重联造成的。即磁场拓扑结构发生了改变,然后将磁能转化为活动星系核中等离子体的动能和热能,并以此来加速等离子体中的部分带电粒子,使得盘内磁场减小,小到低于外围磁场强度,最后形成热辐射与同步辐射相混合,进而反常法拉第旋光起主导作用。
图2给出了b> 0的情况,有14个耀变体源。偏振度随波长变短而增大,dp/dλ< 0,表现出常规去偏振。大致表明在这些耀变体喷流中,吸积盘的内部偏振比外围的偏振高,外围磁场弱,越靠内磁场越强,服从同步辐射的磁场特性。这种情况大约占70%,属于大多数情况。当观测波段小于吸积盘热辐射对应的维恩波长(热辐射的最大波长)时,高频波段的偏振度就大于低频波段的偏振度,与文[14]中光学波段预测的一致。
图3给出了b值的分布直方图。由图可以看出,b> 0的个数多于b< 0的个数,这表明dp/dλ> 0在偏振随波长的变化中起主导作用。b值大致分布在0~0.8,集中分布在0~0.4,图4表明每个耀变体源b值的分布情况,可以明显看出只有6个源位于b< 0,其余的都是b> 0。
由图5可看出,平均磁场主导时湍流指数m的分布情况,b值对应的m值分布直方图。由图6可知,湍流磁场主导时湍流指数m的分布情况,b值对应的m值分布直方图。观测样本的拟合结果与平均磁场主导(法拉第旋转占优)情况和湍流磁场主导(法拉第旋转占优)情况大致一致。表1列出了每个源偏振观测的结果特性,发现OJ 287和OR 103的mR值小于0,这与文[13]的结果不符,其原因不尽相同。可能是因为数据点的不足,或者是在数据的时间段内偏振变化相对较大,从而导致数据的平均值误差较大。
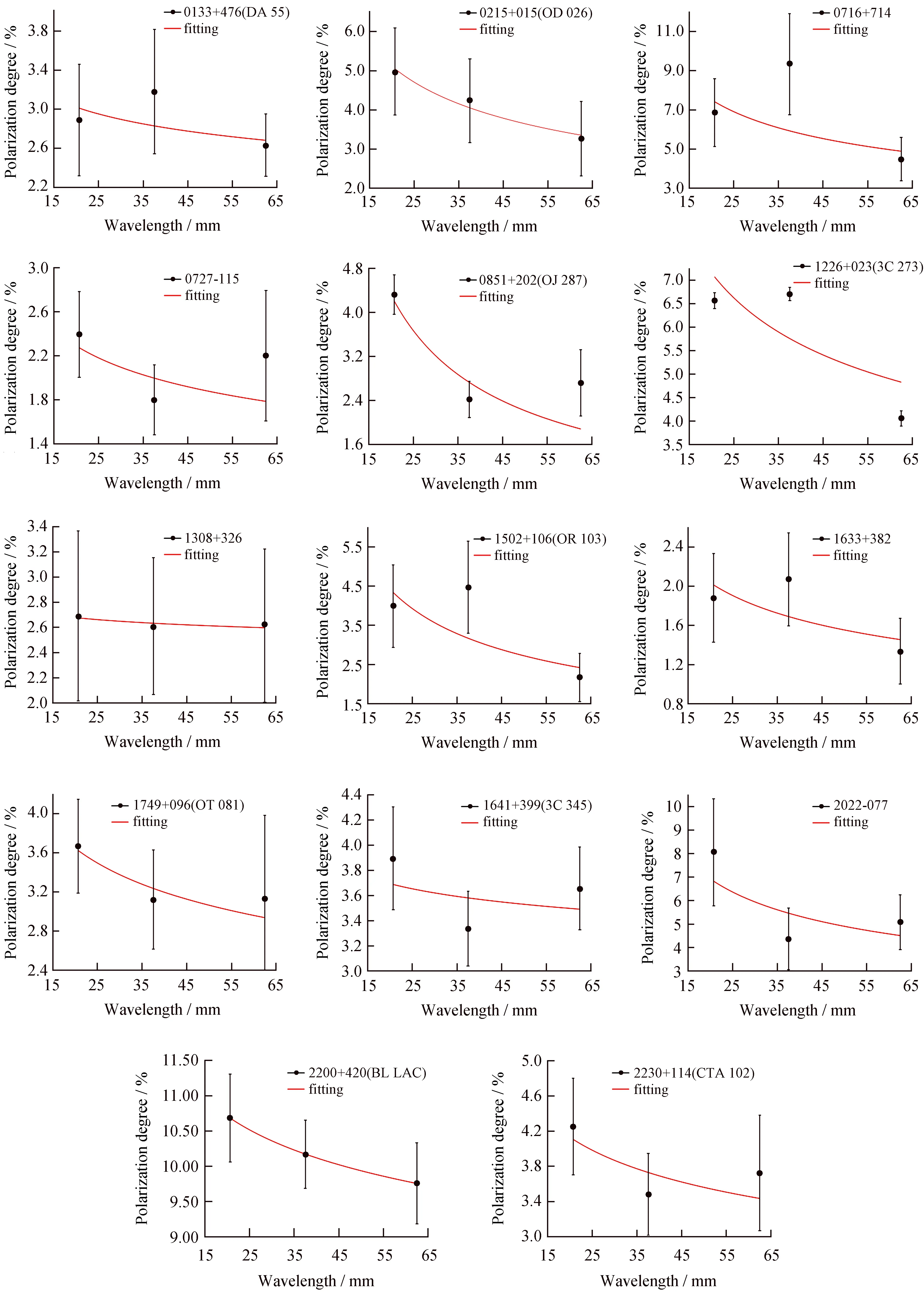
图2b> 0时的耀变体源幂率拟合情况,横轴为波长,纵轴为偏振度
Fig.2 Blazars source power law fitting forb> 0, where the horizontal axis is the wavelength and the vertical axis is the polarization degree

图3b值的分布情况
Fig.3 Distribution ofbvalues
图4 每个耀变体源的b值情况。其中,b> 0代表dp/dλ< 0;b< 0代表dp/dλ> 0
Fig.4b-values for each blazar source. Whereb> 0, stands for dp/dλ< 0;b< 0, stands for dp/dλ> 0
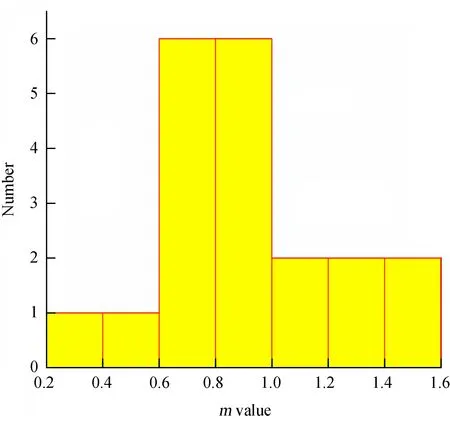
图5 平均磁场主导时湍流指数m的分布情况,每个m值对应于相应的b值,注意到m=2/3对应于三维各向异性柯尔莫果洛夫(Kolmogorov)谱
Fig.5 Distribution of the MHD turbulent indexmin the regular magnetic field dominated case. Each value ofmis derived from the fitting value ofb. We note thatm=2/3 corresponds to the three-dimensional anisotropic Kolmogorov scaling
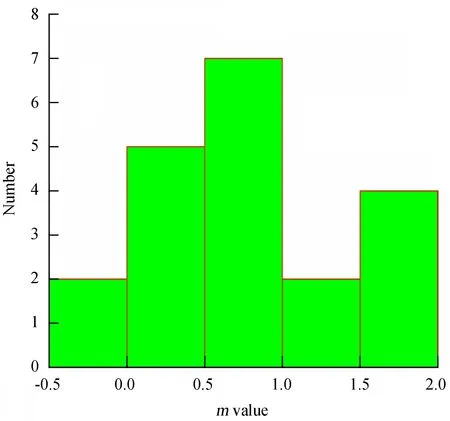
图6 湍流磁场主导时湍流指数m的分布情况,每个m值对应于相应的b值,注意到m=2/3对应于三维各向异性柯尔莫果洛夫(Kolmogorov)谱
Fig.6 Distribution of the MHD turbulent indexmin the turbulent magnetic field. Each value ofmis derived from the fitting value ofb. We note thatm=2/3 corresponds to the three-dimensional anisotropic Kolmogorov scaling
2 讨 论
在拟合的结果中,有两个源0420-014、0805-077的结果为p0(偏振随波长变化不明显)。有14个源的dp/dλ< 0,6个源dp/dλ> 0。耀变体的偏振主要来自同步辐射,但星际介质、吸积盘、宽线区等也会对偏振造成一定的影响。本文只考虑磁场湍流和法拉第旋光的影响,并忽略了以上效应。由于只把电子能谱作为简单的幂率形式,所以内秉偏振度与波长无关,对结果无影响。观察到样本中dp/dλ< 0的去偏振特性,也注意到表1中列出了一些dp/dλ> 0的情况,很难应用磁流体动力学湍流和法拉第旋转解释产生dp/dλ> 0的物理机制,应用反常的去偏振特性,扭曲的磁场可以减少反常的法拉第旋转效应[15]。因此,dp/dλ> 0的去偏振情况是可以发生的。最近,在一些耀变体喷流中发现了常规去偏振(dp/dλ< 0)和反常去偏振(dp/dλ> 0)特性[16]。反常去偏振的耀变体源中反常法拉第旋光起主导作用,反常去偏振相对较少。本文样品中得到的去偏振情况,表明喷流中偏振的特性:热辐射与同步辐射混合后,高频波段的偏振度小于低频波段的偏振度(反常去偏振);当观测波段小于吸积盘热辐射所对应的维恩波长(热辐射的最大波长)时,高频波段的偏振度大于低频波段的偏振度[14](常规去偏振)。
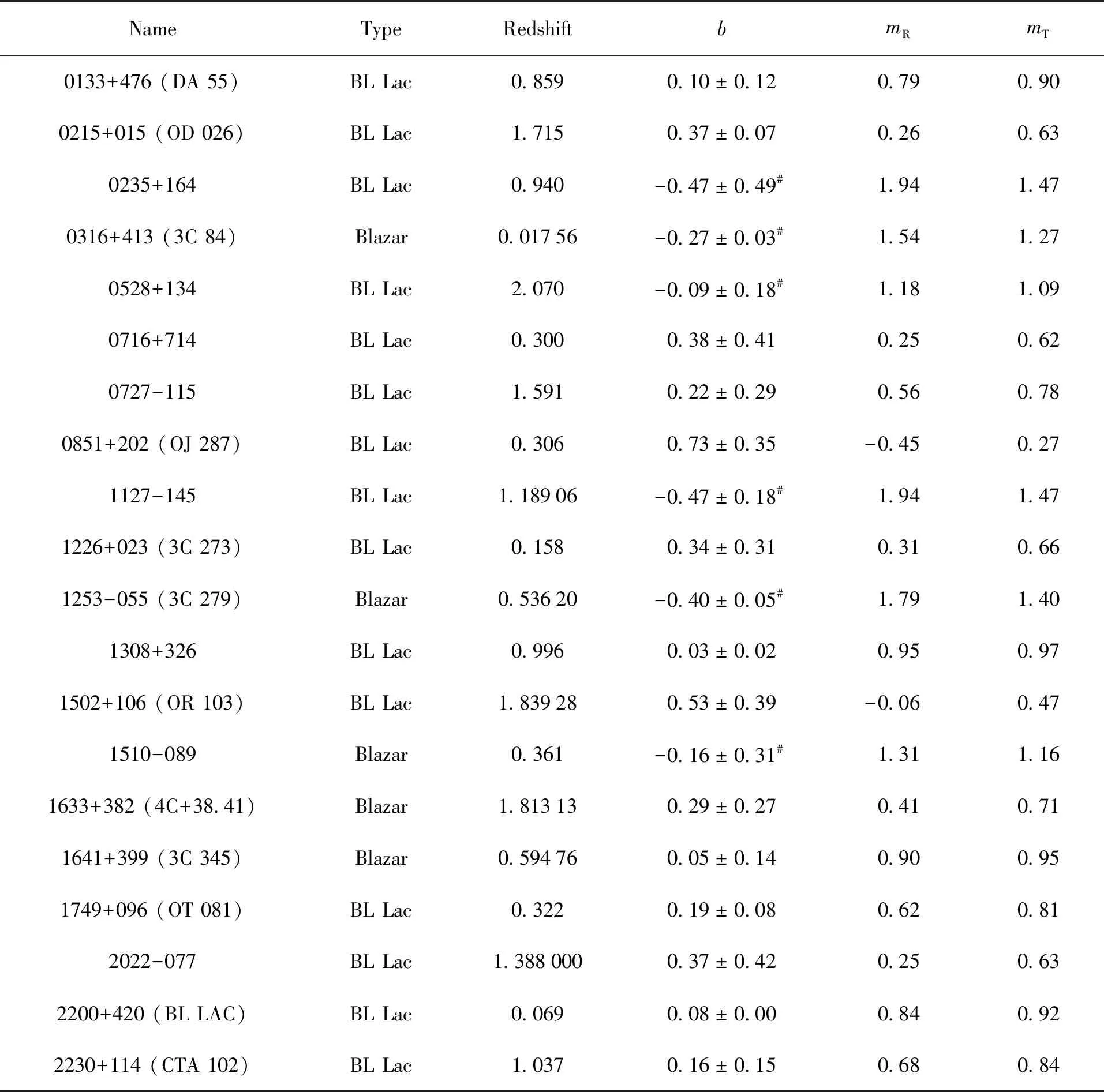
表1 样本拟合结果与波长相关偏振特性总结Table 1 Summary of sample fit results and WDP characteristics
注:mR表示在平均磁场占优情况下得到的磁流体动力学湍流指数,mT表示在湍流磁场占优情况下得到的磁流体动力学湍流指数。(#)代表dp/dλ> 0的耀变体源。
Lazarian & Pogosyan理论分析表明,法拉第旋转波动来自各向异性磁流体动力学湍流。在耀变体样品中的拟合统计结果表明,射电波段的去偏振大致服从柯尔莫果洛夫谱。去偏振和相关的湍流特性表明不同耀变体源的偏振多样性。
对某一耀变体而言,不同波长的射电偏振并不是在时间上同步或准同步观测得到的。在本文中可以看到,样本中大部分耀变体,不同波长的偏振度变化幅度并不大,数据只有3个波段,波段范围也很窄,不利于拟合和分析。文中提到的有关磁场湍流和磁场有序度Π(ν),将在接下来的文章中进一步研究。Π(ν)和湍流对磁场起到的具体作用及物理机制,有着重要的研究价值。
