动态灰色预测模型在崩落法矿山地表沉降预测中的应用
2019-04-18倪振原金爱兵孙金海
倪振原,明 建,金爱兵,孙金海
(1.金属矿山高效开采与安全教育部重点实验室,北京 100083;2.北京科技大学 土木与资源工程学院,北京 100083)
地表沉降现象的产生是一个复杂的过程,影响地表沉降的因素具有复杂多样的特点,主要有地下矿产资源的开采、地表工程的施工、地质结构的变化等因素,这些影响因素或多或少地影响了岩土体的沉降,但不同影响因素对沉降量影响的比重无法准确获得[1-2]。如果能够准确地预测矿区地表沉降的变化量或者趋势,将对矿床开采产生巨大的经济价值和社会意义,因此建立数学或数值模型对地下开采引起的地表沉降进行研究及预测一直是采矿工程和岩土工程领域研究的重点[3-5]。
国内外学者采用很多方法对地表沉降问题进行了预测研究,例如有限单元[6]、灰色系统理论[7-8]、神经网络[9-10]等,分析原理各不相同,分析误差也存在差异。由于地表沉降监测范围大,时间长且监测所得的样本数据较少,适合使用灰色理论建立模型以及分析预测[11-12]。根据现有研究基础,灰色理论模型更适用于短期预测,而对于中长期预测结果更多表现为一种趋势,定量参考价值较低。故本研究将等维新息[13]和等维灰数递补方法[14-15]与灰色预测模型GM(1,1)相结合,建立动态灰色预测模型[16]。以某矿山崩落法深部开采引发的岩层移动及地表沉降数据为数据基础,运用这些模型进行预测和分析,以证明其在预测精度和准确性上比从静态角度考虑未来时刻状态的灰色预测模型GM(1,1)更适于中长期预测。
1 工程概况
该铁矿床采用无底柱分段崩落法开采,其矿岩赋存条件较差。其矿体上部存在公路及输水管道,为此矿山采用预留垂直矿柱的方法进行地下开采。由于深部开采有可能会引起岩层移动与地表沉降,因此需要进行持续的监测工作以避免和降低可能发生的安全隐患。
本研究根据矿区的工程地质和水文地质条件等情况,利用工程现场的地表监测数据,采用理论分析方法,对矿床开采引起的地表沉降变形进行分析和预测,以便根据预测的地表沉降变形及时地调整开采方案,从而降低地面沉降变形诱发地质灾害的机率,其预测结果对矿区的安全生产和社会经济发展有积极的指导作用。
2 灰色预测模型
2.1 GM(1,1)模型建模和精度检验
设定原始数列为:
X(0)={X(0)(i)|i=1,2,…,n}={x(0)(1),x(0)(2),…,x(0)(n)}
(1)
对X(0)作一次累加生成(记作1—AGO),即令
(2)
因GM(n,h)模型中n和h均为1,则GM(1,1)相应的微分方程为:
(3)
式中:α为发展系数;μ反映数据之间的变化关系,即灰色作用量。
根据最小二乘法解得:
(a,u)T=(BTB)-1BTYN
(4)
式中:YN=[x(0)(2),x(0)(3),…,x(0)(n)]T;
进一步得到时间响应系数为:
(5)
还原方程为:
(6)
式(5)和式(6)即为GM(1,1)预测的两个基本模型。
2.2 等维灰数递补模型和等维新息模型
对定量预测而言,随着时间的推移,未来的众多扰动因素将对预测系统施加影响。因此,虽然灰色预测模型GM(1,1)理论上能够实现长期预测,但是从灰平面上观察,仅其最近预测的一两个数据的精度较高,剩余数据更多是反映一种趋势。
等维灰数递补模型的建立过程:首先用已知数据建立灰色预测模型GM(1,1)预测最近一期值,其后将预测值补充到已知数列中,再去掉最老的数据;序列再建立GM(1,1)模型继续预测,依次循环,直至完成预测目标。该模型的特点是能够及时补充和利用灰信息,提高灰平面的白色度,缩小预测值的灰区间;每预测一步,即对灰参数作一次修正,并随之修正模型;可以使用较短的数列完成相对长期的预测,但是不能无限地预测下去。
等维新息模型的建立过程与等维灰数递补模型相似,但是等维新息模型替补的数据为系统获得的实际数据,而等维灰数递补模型替补的数据为预测值。因此,前者是用新息来调整模型,后者则是用灰数来约束灰平面的大小。故在实际处理问题时,可以将两种方法结合起来应用,从而实现中长期预测的目标。
3 灰色组合预测模型的实例分析
本文以山东某矿E12点沉降测量数据为例,验证等维新息预测模型和等维灰数递补预测模型结合应用于地表沉降的中长期定量预测的可行性。该点从2016年8月开始测量,令其初始测量值为0。实际测量值如表1所示。
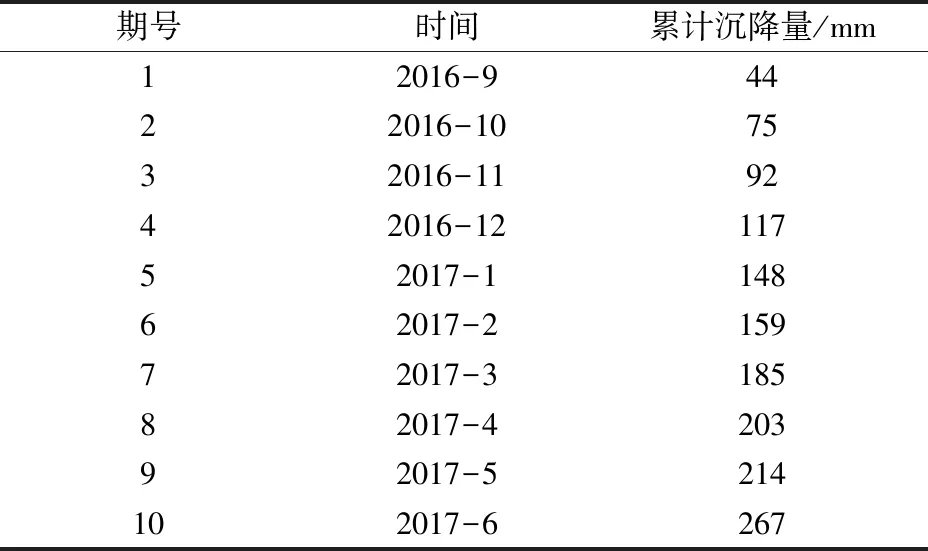
表1 E12监测点沉降测量数据
3.1 灰色预测模型与等维灰数递补模型的对比
依据灰色预测模型GM(1,1)的数据要求为非负值,且其第1项不能为0的原则,取2016年9月至2017年2月的6期数据作为原始数列,2017年3月至2017年6月的数据作为对比。其预测结果如表2所示。
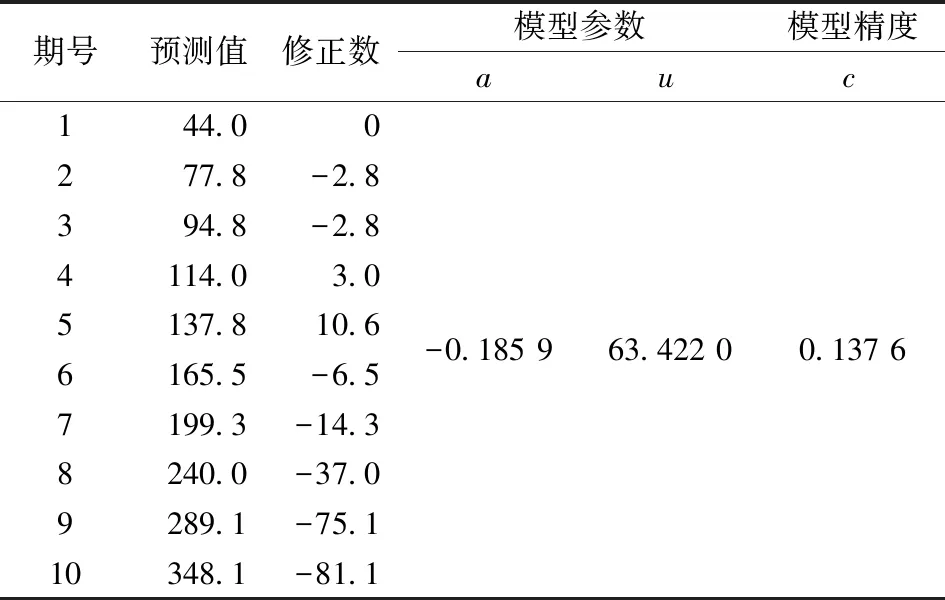
表2 灰色预测模型GM(1,1)预测结果
由表2数据可知,对于灰色预测模型GM(1,1),作为短期预测值,其预测的数据值仅仅只有最近1~2个数据具有实际意义。而随着时间推移,预测值与实际值之间的差距逐渐扩大,不再具有实际意义。此时需要对该模型进行修正,将原始数据进行滑动平均处理,利用等维灰数递补方法将第7期所预测值带入新的模型中,并去除第1期的数据,预测第8期的数据,以此循环建模,可以获得较好的预测结果。
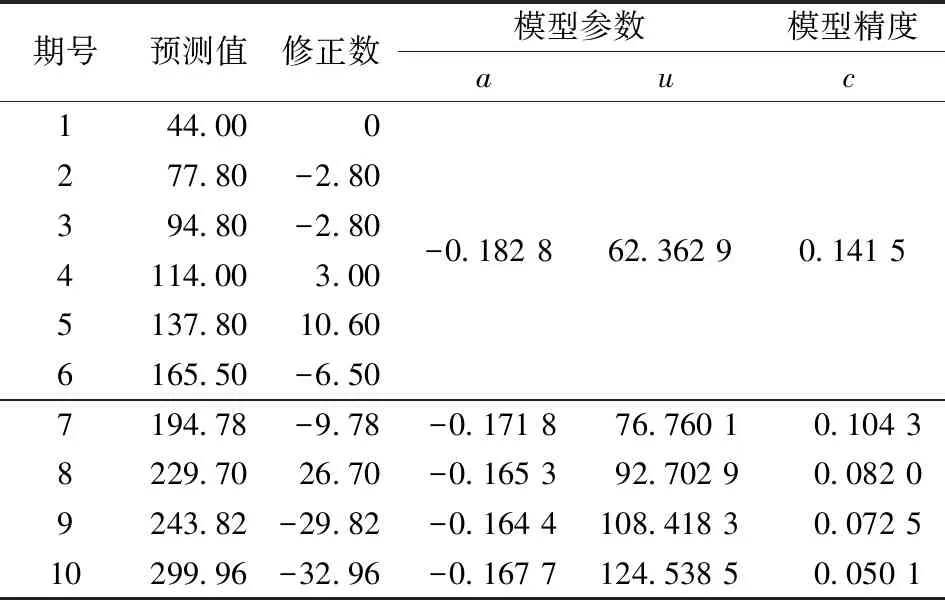
表3 等维灰数递补模型预测数据
由表3可知,应用等维灰数递补方法能够较灰色预测模型GM(1,1)降低40%~50%的预测误差,精度得到了较大的提升,经过修正后可进行中长期的预测,但随着时间的推移仍存在一定的误差,因此也不能无限地预测下去。
3.2 两种动态灰色预测模型组合预测
由以上所得,等维灰数递补方法可在一定程度上提高模型预测精度,故可利用等维新息方法将已知的实测数据带入模型中进行预测,即将第7期实测数据代入模型中,去除第1期数据,得到新预测值;再将第8期实测数据代入模型中,去除第2期数据,如此循环递补。而后将无实测数据部分利用等维灰数递补方法进行预测,此时所得预测数据的精度将进一步提高,模型的预测值与实际值进一步接近。因此本研究将前10期数据由等维新息预测模型预测,11至15期数据由等维灰数递补预测模型预测,预测的结果如表4所示。
动态灰色预测模型组合预测结果与各单体预测模型之间的修正数比较,如图1所示。
由表4和图1可知,应用等维新息预测模型获得的第1至10期预测结果与表3中应用等维灰数递补预测模型获得的预测值进行比较,前者误差得到进一步的降低,灰色模型的预测精度得到进一步的提高,更趋近于实测值;同时,利用等维灰数递补预测模型预测的第11至第15期数据也符合之前实测值的增长趋势,不存在较大偏差。
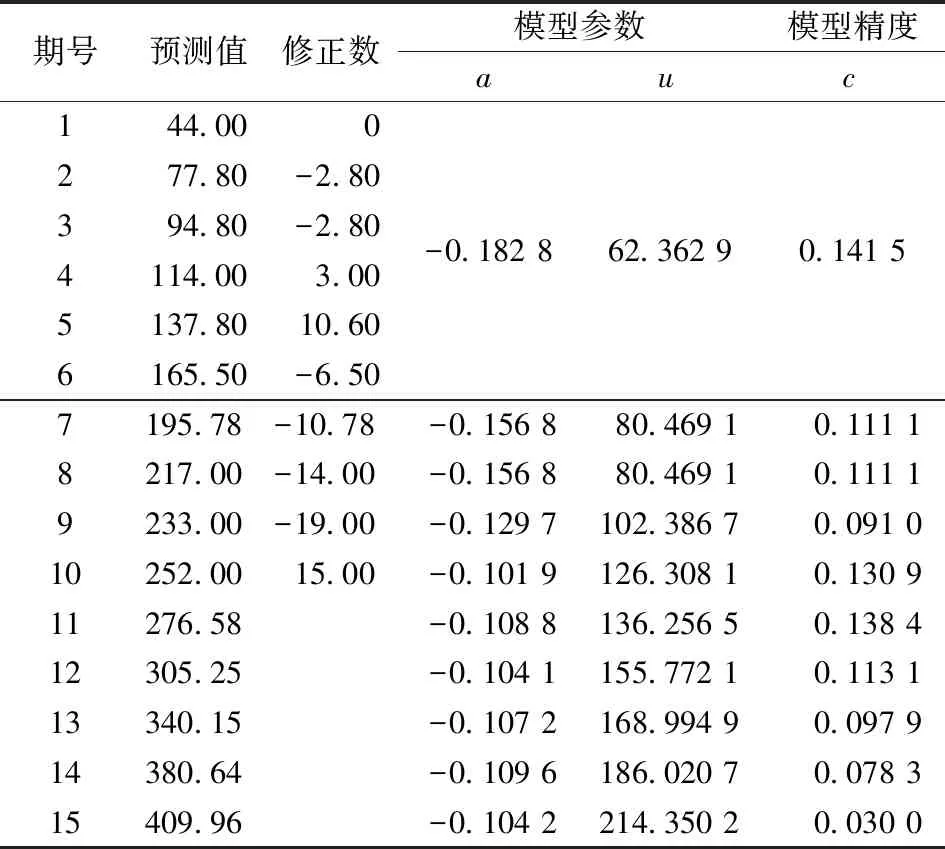
表4 两种动态灰色预测模型组合预测结果
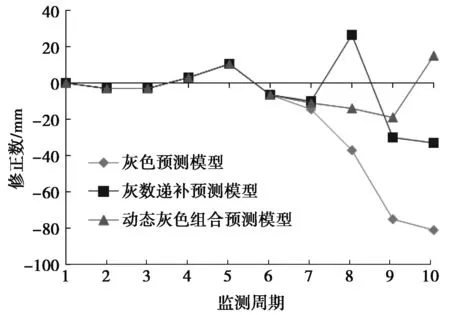
图1 灰色预测模型修正数比较Fig.1 The residuals of the forecasting models
试验结果表明,将等维灰度递补方法和等维新息方法结合运用于灰色系统中,及时添加新息并去除老数据,并利用新息调整模型、灰数约束灰平面大小的方法进一步提高了模型的预测精度、减少了预测误差,较单独使用等维灰数递补方法的灰色预测模型的预测值更趋近于实测值。虽然两种动态灰色预测方法能够大幅度地减少预测误差,提高模型精度,但也无法无限地进行长期预测,需要在获取实测数据后及时将其添加入系统,通过新息调整模型,提升精度。
4 结论
针对某铁矿床应用无底柱分段崩落法开采深部矿体时矿区地表沉降数据的特点,本研究以灰色预测模型GM(1,1)为基础,采用等维新息和等维灰数递补两种动态灰色预测方法对矿山地表的沉降量进行了中长期预测研究。研究结果表明动态灰色预测模型的预测结果与实测数据趋势一致性较高,其预测精度有较大提高。该模型适用于矿区地表沉降的中长期预测,能够为降低矿床开采和矿区地表的安全隐患提供依据。
