基于多元线性回归分析的乘用车质心高度预估

郑羿方，卢萍



基于多元线性回归分析的乘用车质心高度预估

郑羿方，卢萍

（广州汽车集团股份有限公司汽车工程研究院，广东 广州 511434）

整车质心高度是汽车动力学的重要参数之一，对整车侧向稳定性及车辆纵倾均有较大影响，是汽车动力学开发及仿真必不可少的参数。在概念设计阶段初期，由于车辆造型及详细布置方案均未确定，无法通过数模计算，获取较为准确的整车质心高度值。文章利用公开的已上市乘用车基本参数，通过回归分析，逐步提取概念设计阶段已知的整车参数中对整车质心高度影响较大的参数，建立整车基本参数与质心高度间的多元线性回归关系，并通过已量产整车项目及其对标车，验证所建立的多元线性回归关系的预估准确性。上述多元线性回归关系可在项目早期为汽车动力学开发仿真提供较为准确的整车质心高度值，也可用于评价下线样车质心高度与对标车的趋合程度。

整车质心高度；多元回归分析；概念设计

引言

本文介绍利用整车项目概念设计阶段已知的参数，运用多元线性回归分析，预估整车质心高度的方法。整车质心高度作为汽车动力学开发及仿真必不可少的参数，对车辆的侧向稳定性及纵倾影响较大。准确的预估整车质心高度，对底盘的硬点设计，悬架弹性件匹配以及底盘调校骡子车的重量配载都至关重要。汽车动力学性能开发始于概念设计阶段，在概念设计阶段初期，只有立项时确定的整车基本尺寸参数及部分关键总成参数，车辆内外造型及详细布置方案均未确定，因此无法通过数模计算，获取较为准确的整车质心高度值。一般是通过测量尺寸及配置相近的对标车质心高度作为整车质心高度目标的初值，但实际的样车质心高度往往与对标车有一定偏离，有时偏离较大，造成样车下线后部分底盘动力学性能无法达成目标，而重新匹配底盘参数又将带来其他性能的牺牲以及项目周期的延后。本文利用大量对标车的测量数据，通过从一元到多元的线性回归分析，逐步提取项目概念设计阶段已知参数中对整车质心高度影响较大的参数，建立起预估整车质心高度的多元回归方程。同时利用已量产的整车项目及其对标车的质心高度测量值，验证所得回归方程的预估准确程度。

上述多元回归方程既可用于项目开发初期的质心高度预估，也可用于评价样车质心高度与对标车平均水平的趋合程度。

1 整车质心高度影响因子的候选范围

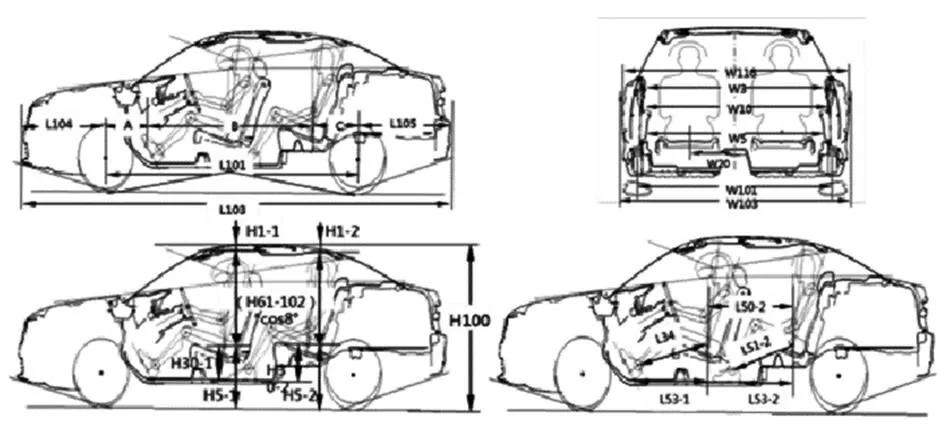
图1 概念设计阶段可确定的整车基本尺寸参数

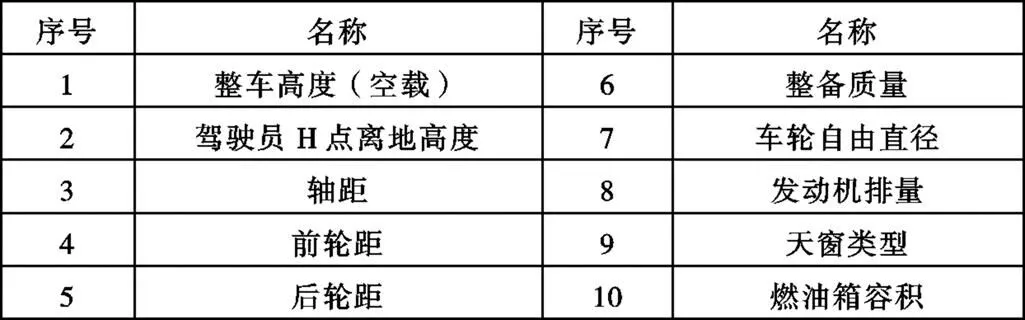
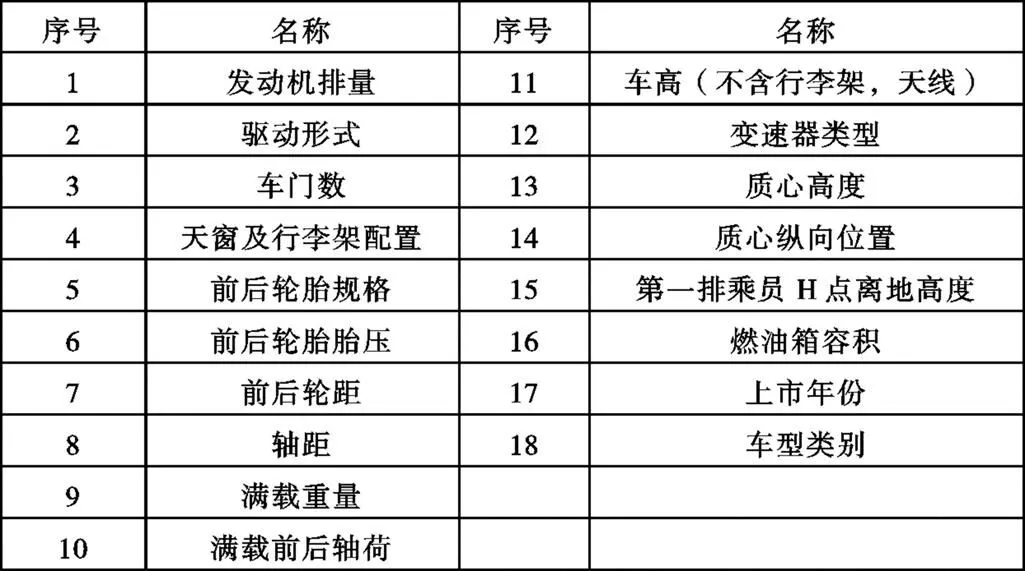
整车质心高度是汽车所有总成及零部件在Z向布置后得出的结果，因此只要知道每个零部件的重量及其质心相对地面的高度后，自然可以求得整车质心高度。然而在项目开发中实际遇到的矛盾是，在概念设计阶段，整车总体布置与底盘概念设计同时进行。对整车质心影响较大的总成及零部件的重量及质心位置未能确定，但底盘的概念设计需要输入整车质心高度用于计算仿真。因此依靠零部件重量及几何布置确定整车质心高度，无疑与在概念设计阶段就输出较为可信的整车质心高度的目标背道而驰。因此，本文将质心高度影响因子的选取范围限定在概念设计阶段可获取的信息，一般在总体技术方案中体现，大致包含两类信息：（1）整车基本尺寸参数，如整车外廓尺寸，人机布置尺寸，见图1；（2）关键总成及零部件参数，如发动机排量，座椅数量，轮胎型号，天窗的有无及其类型，油箱容积，是否为四驱等等。剔除其中与质心高度无关联的因子，并考虑公开途径获取对标车相应因子信息难易度后，列入分析的候选因子共10项，见表1。

表1 整车质心高度影响因子候选范围

2 分析方法简介

由于影响整车质心高度的因素是多方面的，而每个因素的影响程度有所不同。多元线性回归分析可以直观快速的量化每个候选因子对整车质心高度影响的显著性，只要采用的模型和数据相同，通过标准的统计方法可以计算出唯一的结果。是合适的预估整车质心高度的方法。通过线性回归分析，最终提取影响整车质心高度的显著因子，组成预估整车质心高度的多元线性回归方程。

多元线性回归方程可表示为如下的形式：

其中0到β为未知数，称为回归系数，可以通过最小二乘法求得。1到x为自变量，对应上一章所选取的10个候选因子。是随机误差。

多元线性回归方程的校验，主要采用校正的决定系数adjusted2。计算公式如下：

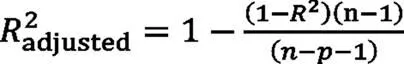
式中2是决定系数，n为样本数量，为特征数量，与式（1）中值相等。2_adjusted取值在[0,1]，越接近1说明线性回归方程的预估拟合性越好。如果增减或更换候选因子后得出的adjusted2值更接近1，则认为采用的因子是影响质心高度的关键因子，反之则认为增减或更换的因子对整车质心高度没有显著影响。以此逐渐筛选出候选因子中影响整车质心高度的关键因子。

3 样本信息介绍

为了使整车质心高度预估结果具备较好可信度，样本数量及样本的覆盖范围必须达到一定的规模。作者通过公开途径共获取超过500台车型的样本数据。考虑到目前在市场占主导地位的车型特点：（1）承载式车身结构；（2）前驱车型。本文筛选出124台满足上述特点的乘用车数据作为分析样本，其中轿车75台，SUV车型49台。车型上市时间跨越2012年至2018年。以轴距划分车辆等级后，不同等级车型所占比例见图2，3：

图2 SUV样本不同级别车型所占比例

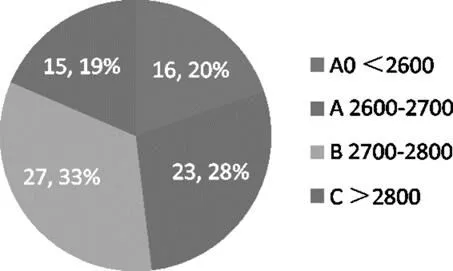
图3 轿车样本不同级别车型所占比例

上述车型样本中包含的数据类型见表2。

表2 车型样本包含的数据类型

上述数据的测量方法均采用统一的标准，同一类型数据由相同设备及机构测量得出，因此具备可靠性。由表可见，车型样本提供的数据完全满足分析的需要。考虑到轿车与SUV车型在外廓尺寸以及配置上存在一定差异，在后面的章节中将单独对轿车及SUV进行分析，并分别给出两者的整车质心高度预估多元回归方程。

4 基于多元回归分析的整车质心高度预估

4.1 一元回归分析

当所知整车参数非常有限，且对整车质心高度预估准确度要求不高的情况下，可以采用整车高度预估整车质心高度。美国国家公路交通安全管理局在开展车辆“鱼钩试验”及“正弦迟滞”试验时，即采用整车高度估算整车质心高度，为测量车辆动态数据的陀螺仪的安装位置提供参考[1]。

在分析中采用的整车高度为空载下，不含行李架及天线的钣金处整车高度。通过对样本进行分析，所得整车高度与整车质心高度关系及校验结果如下：

预估所得质心高度与实际测量的质心高度对比见图4，图5。

从图4，5可以看出，整车高度与整车质心高度间存在一定的线性关系，但是部分样本的预估值与实际测量值偏离较大，最大残差达37mm和21.3mm，因此有必要引入更多因子，提升预估准确性。

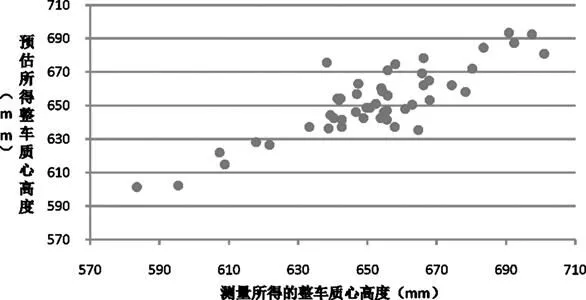
图4 SUV车型测量质心与预估质心的对比

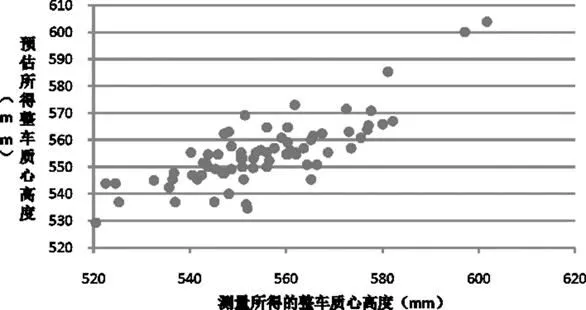
图5 轿车车型测量质心与预估质心的对比

4.2 多元回归分析

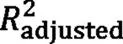
4.2.1二元回归分析

将第一章节中选定的因子逐个与整车高度搭配进行二元线性回归分析，所得校验结果见表3，4。

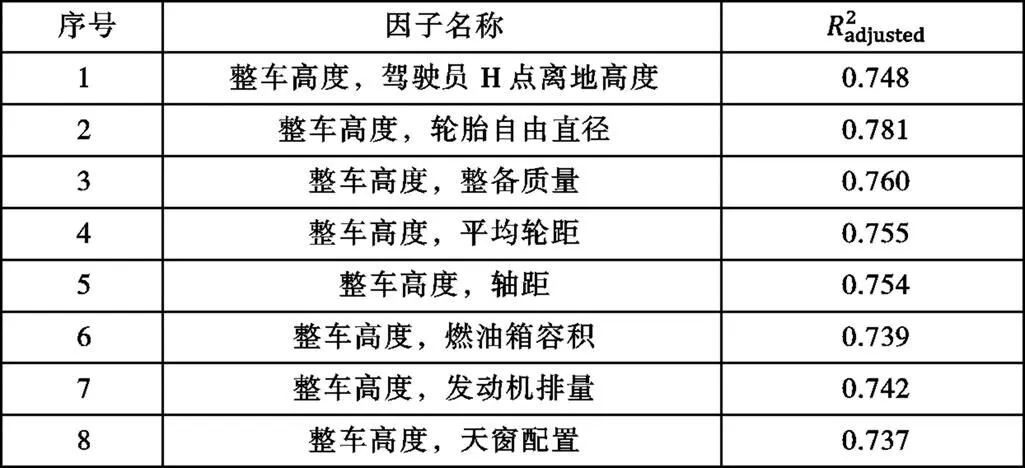
从校验结果看，影响SUV及轿车质心高度的因素有不同。SUV受轮胎直径影响大，原因可能是因为SUV间的离地间隙差别较大，大的轮胎往往提供更大的离地间隙，从而提高整车质心高度。而轿车间的离地间隙差别较小，因此顶端的质量，如是否搭载天窗，对质心高度的影响变得更为显著。

4.2.2三元回归分析

4.2.3四元回归分析

四元回归分析所得校验结果见表7，8。

4.2.4五元回归分析

五元回归分析所得校验结果见表9，10。

4.2.5六元回归分析

六元回归分析所得校验结果见表11，12。

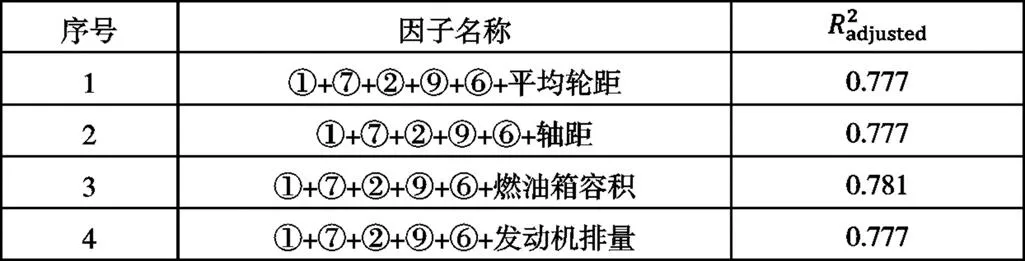
4.2.6七元及以上的回归分析

七元及以上回归分析所得校验结果见表13，14。

从校验结果可以看出，继续增加因子，无论是SUV还是轿车，对整车质心高度的预估准确性均起不到正面作用。

4.3 提取关键因子及获取最终多元回归方程

由上述的分析可以筛选出影响SUV及轿车整车质心高度的关键因子，见表15。

表15 影响整车质心高度的关键因子

所得的多元回归方程如下：

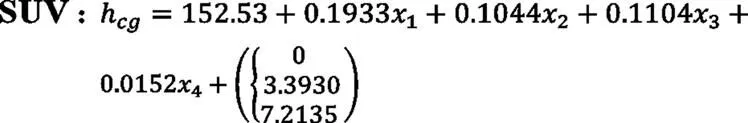
其中：x1是整车高度，x2是车轮自由直径，x3是驾驶员H点离地高度，x4是整备质量，0对应无天窗，3.393对应小天窗配置，7.2135对应全景天窗配置。

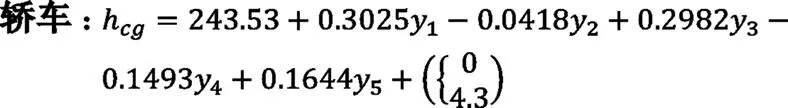
其中：y1是整车高度，y2是驾驶员H点离地高度，y3是油箱容积，y4是平均轮距，y5是车轮自由直径，0对应无天窗，4.3对应带天窗配置。

5 多元回归方程预估准确性验证

表16 SUV信息

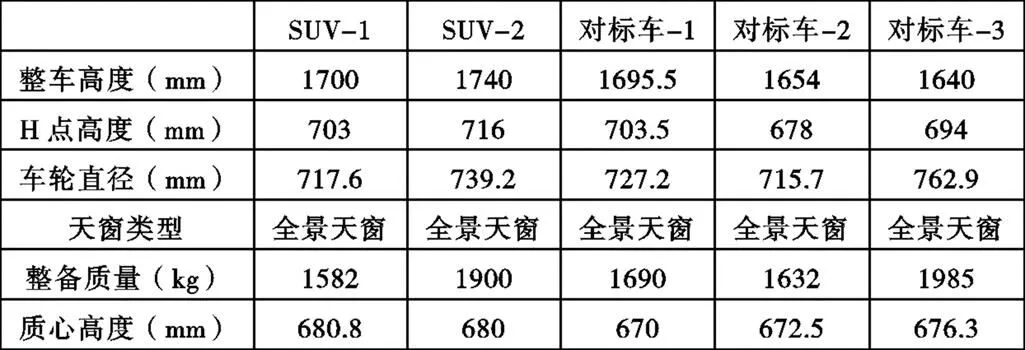
为验证所获得的多元回归方程预估整车高度的准确程度，选取一批按同一标准及设备测试获得质心高度的轿车及SUV，包含自主研发车型及其对标车，对比其预估所得整车质心高度与测量值的差距。上述车辆均不属于获取多元回归方程所用的车辆样本。车辆信息见表16，17。

表17 轿车信息

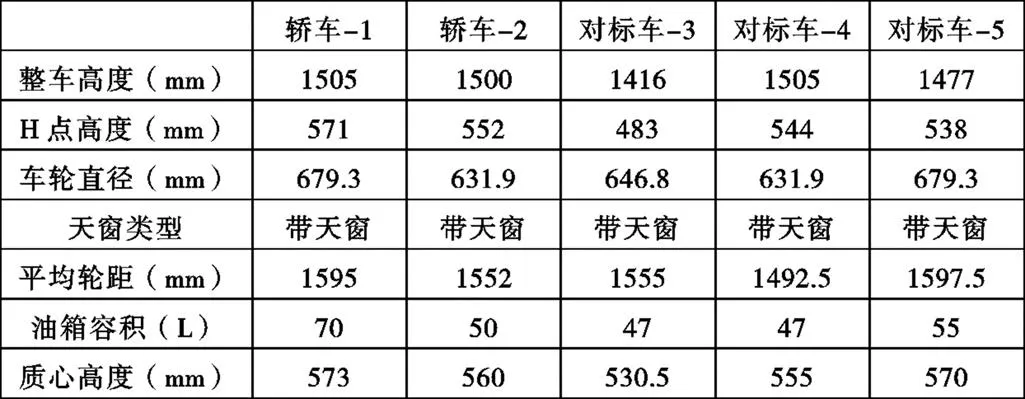
将上述信息分别代入整车质心高度多元回归方程中，所得结果及与质心高度实际测量值误差，经四舍五入保留一位小数后，见表18，19。

表18 SUV预估质心高度及误差

表19 轿车预估质心高度及误差

从验证结果看，多元回归方程可较准确的预估整车质心高度，其中，SUV整车质心高度预估平均误差-9.8mm，最大误差-18.5mm，最大误差幅度小于3%。轿车整车质心高度预估平均误差6.6mm，最大误差20.5mm，最大误差幅度小于4%。可以满足底盘概念设计阶段对质心高度的精度要求。

6 结论

本文以轿车及SUV车型为研究对象，针对概念设计阶段初期可确定的车辆参数，通过多元回归分析，提取其中影响整车质心高度的关键参数，通过分析，确定了影响SUV质心高度的关键参数五个，影响轿车质心高度的关键参数六个，并获取由相应参数组成的整车质心高度预估多元回归方程。随后利用自主研发车型及其对标车对多元回归方程预估准确性进行验证，结果表明所获取的方程可较好的对整车质心高度进行预估，预估精度满足在项目概念阶段输出较准确的整车质心高度的要求。该结果可用于项目开发初期的质心高度预估，也可用于评价样车质心高度与对标车平均水平的趋合程度。

[1] TP-126,Laboratory Test Procedure For FMVSS 126, Electronic Stabi -lity Control Systems, NHTSA,September 9,2011.

Estimation of Passenger car Center of Gravity Height Based on Multiple Linear Regression Analysis

Zheng Yifang, Lu Ping

( GAC R&D Center, Guangdong Guangzhou 511434 )

Vehicle center of gravity height, as an important vehicle dynamic parameter which gives a big influence towards vehicle lateral stability and pitching, is essential for vehicle dynamic development and simulation. In the conceptual design phase, since the style and detailed packaging plan is not settled down yet, a precise vehicle center of gravity height cannot be derived through 3D model calculation. This passage takes the advantage of basic parameters of passenger cars already debut in the market, through multiple linear regression analysis, to extract the parameters, among those already known in the conceptual design phase, which gives significant influence to vehicle center of gravity height and establish the multiple linear regression relation between those basic parameters and vehicle center of gravity height. Then evaluate the accuracy of the multiple linear regression relation by using vehicle projects already SOP and their benchmark cars. The above mentioned multiple linear regression relation could be used to provide vehicle center of gravity height with good precision for vehicle dynamic simulation.

vehicle center of gravity heigh; multiple linear regression analysis; conceptual design

U467

B

1671-7988(2019)07-84-05

郑羿方，硕士学位，就职于广州汽车集团股份有限公司汽车工程研究院，工作方向为整车性能集成。

U467

B

1671-7988(2019)07-84-05

10.16638/j.cnki.1671-7988.2019.07.029