水平钻井环空岩屑床表面颗粒临界启动流速的影响因素
2019-04-17孙晓峰袁玉金张克博胡乔波
孙晓峰,汤 捷,袁玉金,张克博,陈 烨,胡乔波
(1.东北石油大学 石油工程学院,黑龙江 大庆163318; 2.中油国际拉美公司,巴西 里约热内卢 999074)
水平井的大斜度和水平井段钻进过程中,当停止循环(如接单根作业)或钻井液排量较低时会引起环空岩屑沉降并堆积于井眼低边,形成稳定的岩屑床。岩屑床会导致钻柱扭矩增大、拖压等问题,室内实验和现场实践均表明,井斜角>50°时造斜井段和水平井段岩屑沉积最为严重[1-3]。

图1 环空内床面颗粒控制体几何示意图Fig.1 Geometric sketch showing particle control body in annulus
目前用于描述岩屑运移理论模型可以分为2类,一类理论假设和实验观察结合的固液分层计算模型,如两层岩屑运移模型[4-5]、三层岩屑运移模型[6-8],可以用于计算岩屑床沉积高度、运移效率等参数;另一类是计算钻井液携岩运移时所需的临界流速预测模型[9-10],以临界流速抑制岩屑床生成,保持井眼清洁。相比较而言,临界启动流速预测模型易于理解其物理意义,可以直接用于指导现场工程人员优选排量。
临界流速预测模型中的拖拽力与拖拽系数有关,因拖拽系数经验模型众多,如何选择模型,现场工程人员并不容易掌握。本文应用边界层绕流速度基本原理解析求解颗粒表面切力,并将拖拽力用表面切力代替,结合举升力和颗粒间相互作用力,建立床面颗粒临界启动流速模型。
1 岩屑床床面颗粒受力分析
经过大量文献调研,在不影响计算精度的情况下,建立模型之前做以下假设:①钻井液为不可压缩介质;②实际不规则岩屑颗粒用相同颗粒直径和球形度的球体颗粒代替;③实际岩屑床面用平均床面代替;④钻井环形空间为同心环空,且钻杆不旋转。根据以上假设条件,对床面岩屑颗粒的启动过程进行分析和模型推导。
1.1 床面岩屑颗粒表面切力
1.1.1 环空表面绕流切力
井壁与钻杆形成的环形空间存在钻杆壁面和井壁2个壁面,因此环空钻井液具有双速度梯度分布的特点,环空某一直径环形曲面存在最大流速(图1)。
设最大速度环形曲面对应半径Rc,根据E.Bobok[11]给出的表达式计算
(1)
式中:Ri为钻杆外部半径;Ro为井眼内部半径。
引入参数颗粒沉陷度,其定义为床面颗粒相对岩屑床床面陷入的程度
(2)
式中:ζ为颗粒沉陷度;ζ′为颗粒最低点距平均床面距离;rs为岩屑颗粒平均半径。
如图2所示,沿圆周选取计算点处为原点建立直角坐标系,绕体积微元圆周位势流速度分布为
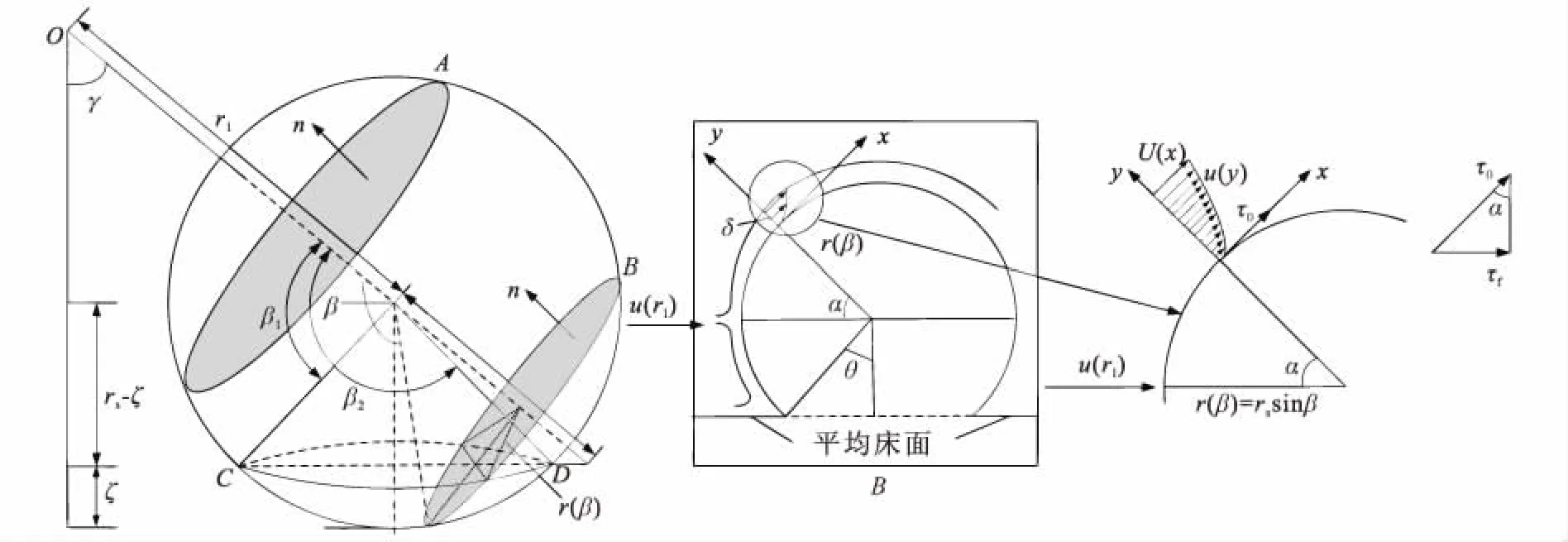
图2 环空岩屑床床面不同位置(γ角)处颗粒启动几何示意图Fig.2 Geometry sketch showing particle initiation at different positions (γ angle) of the annulus cuttings bed
(3)
式中:u(rl)为各层体积微元对应主流速度;rl为颗粒中心距中轴线距离。
环空内最大流速umax可以表示为
(4)
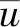
环空内的速度分布表达式整理为
(5)
式中:卡门常数κ=0.41。当速度分布在Ri→Rc间时,i=1,ΔR=Rc-Ri;当速度分布在Rc→Ro间时,i=2,ΔR=Ro-Rc。u*为摩阻流速,即表面切应力与钻井液密度比值的平方根;u*1为杆外壁摩阻流速;u*2为井眼内壁摩阻流速。
表面切力表达式为
(6)
ff为液流平均摩阻系数,利用Colebrook-White[12]公式计算
(7)
式中:ε为平均表面粗糙度;Dh为有效水力直径;Re为液流雷诺数。
假设计算点处的速度分布与距颗粒表面垂直高度y满足u(y)=ay2+by+c,且边界条件满足
(8)
由冯·卡门动量积分方程[13]化简整理得到
(9)
式中:rβ为β角对应面积微元半径;ν为流体运动黏度。
流体运动黏度根据下式计算
(10)
式中:n为幂律指数;K为稠度系数;ρ为钻井液密度。
边界层厚度δ(α)为
δ(α)=
(11)

(12)
根据该假设条件可得
(13)
其中:b=2u(rl)/(15νrβ)。
作用于微元圆周任一点处切力为
(14)
该点切应力沿着未分离圆周积分,再沿轴线l纵向积分得总切力Fτa

(15)
函数F(a)通过积分上限函数与积分值回归得到
F(a)=-0.1359a3+1.0201a2-0.5179a+0.0426
(16)
式中:θ为颗粒沉陷处点至颗粒中心的连线与竖直方向的夹角。
β1、β2分别满足
(17)
式中:γ为颗粒在床面的位置角(图2)。

图3 床面颗粒边界层绕流计算几何示意图Fig.3 Geometrical sketch showing the flow calculation of cuttings bed boundary layer
1.1.2 床面边界层绕流切力
床面颗粒除受到环空速度梯度的影响,还受到床面黏性底层内切力作用,用Fτb表示。如图3所示,体积微元C从黏性底层外边界积分至内边界,边界层厚度为

(18)
式中:fb为床面的平均摩阻系数;τb为平均床面切力;δp为床面边界层厚度。
同时
(19)
式中:βout为黏性底层积分外边界角,指由顶部到黏性底层外边界的张角;βin为黏性底层积分内边界角,指由颗粒顶部至与平均床面接触点处张角(图3)。
黏性底层内部速度分布[13]为
(20)
自颗粒顶端向下积分,积分表达式为
(21)
黏性底层内部床面边界层切力与外部环空表面切力叠加,得沿流动方向总表面切力Fτ
Fτ=Fτa+Fτb
(22)
1.2 床面颗粒举升力
液流流经床面颗粒还受举升力作用。岩屑床沉积程度不同,床内流速ud求解方法不同。
1.2.1 岩屑沉积密实
流态为层流,根据线性达西渗流公式
(23)
式中:Kp为岩屑床渗透系数;Δp/L为L测量段内的压降梯度;μ为钻井液动力黏度。
1.2.2 岩屑沉积非密实
流速较大时,根据Forchheimer归纳实验数据给出的非达西渗流二项式求解
(24)
式中:βD为非达西系数。
非达西系数按J.Geertsma[14]的表达式计算
(25)
式中:q为岩屑床平均孔隙度(体积分数)。
由Kozeny-Carman[15]多孔介质渗透率Kp的求解公式可得
(26)
式中:c0系数取0.2;Ms为颗粒比表面积,球体颗粒的Ms=3/rs。
(27)
式中:Δps为颗粒上下压力差值;As为垂直于液流方向颗粒的投影面积。
1.3 颗粒间相互作用力
颗粒与颗粒之间还存在黏结力作用。黄长伟等[16]转化得到的黏结力表达式
(28)
式中:ξs=4.744×10-6kg/m;指数m=10。
关于干容重与容重比值j,根据文献[17]对现场实际与室内资料分析研究所得表达式计算
(29)
式中:δs为颗粒表面薄膜水厚度,韩其为[18]建议取0.4 μm;r0为参考颗粒半径,取0.5 mm。
2 临界启动流速模型
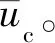
(Fτa+Fτb)·L1+(FL-FP)·L2-Fg·L3>0
L1=rs·(1-ζ)
L2=rs·sin[arccos(1-ζ)]
L3=rs·cos[φ-arccos(1-ζ)]
(30)
式中:φ为井斜角;Fg为颗粒在钻井液中所受浮重
(31)
式中:ρs为岩屑平均密度。


图4 床面颗粒启动临界流速模型计算流程图Fig.4 Flow chart of calculation of critical incipient velocity model for cuttings bed particle
3 床面颗粒临界启动流速模型与实验对比
3.1 清水为循环介质的实验对比
在现场实际中,一般采用清水作为钻井液介质,故室内实验以清水为介质;实验颗粒直径为2 mm和3 mm,且密度与实际岩屑相近。井筒内直径为120 mm,钻杆外直径73 mm,井斜角为70°。颗粒启动过程中,应用高速相机捕捉颗粒瞬态启动时刻,图像帧率为0.025 s 。
如图5所示,模型预测值随床面高度变化不大,无因次床面高度>0.3时与实验测量的数值符合较好。预测值与实验值的绝对误差控制在0.60%~13.07%,绝对平均误差为6.41%。当颗粒直径为2 mm时不需要修正;颗粒粒径为3 mm时,模型预测值与实验对比表明误差较大,因未考虑压差阻力影响,故引入表面切力修正系数。设压差阻力为表面切力的b倍。根据颗粒直径范围分段修正,当颗粒直径为3~3.3 mm时,b=0.6。经过修正以后临界启动流速预测值与实验值接近,绝对误差在2.51%~16.66%之间,绝对平均误差为8.80%。

图5 井斜角为70°时临界流速预测值与清水实验数据对比Fig.5 Comparison of the predicted value of critical flow velocity with the experimental data of water with drilling well angle of 70°(A)颗粒直径2 mm; (B)颗粒直径3 mm
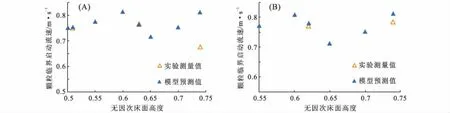
图7 粒径=0.45 mm时临界流速预测值与PAC溶液实验值对比Fig.7 Comparison of the predicted value of critical flow velocity with the experimental data of PAC solution (particle size 0.45 mm)(A)井斜角90°; (B)井斜角70°
当井斜角为90°时(图6),该实验颗粒直径范围为3~3.3 mm,同心环空井筒内壁直径203.2 mm,钻杆直径101.6 mm;当颗粒直径>3 mm时,实验测得的临界启动流速随床面高度变化不大,引入修正系数b=0.7,模型的预测临界流速与实验测量值符合得较好,绝对平均误差为4.84%,绝对误差最大为8.33%,最小仅为0.29%。

图6 井斜角90°时临界流速预测值与清水实验数据对比Fig.6 Comparison of the predicted value of critical flow velocity and the experimental data of water with drilling well angle of 90°
3.2 PAC溶液为循环介质的实验对比
当循环介质为具有一定黏度的PAC溶液时,将模型计算的临界启动流速与M.Q.Duan等[3]实验数据进行对比(图7、图8)。 M.Q.Duan等的文献中实验用颗粒直径分别为0.45 mm和1.4 mm,同心环空井筒内壁直径203.2 mm,钻杆直径101.6 mm。
如图7-A所示,临界启动流速先增后减,变化区间较小,无因次床高0.45~0.7时,模型计算值符合实验规律,绝对平均误差为7.06%,最大误差达到了20.25%;但此时无因次床面高度为0.75,超出了0.45~0.7的适用范围。当床面高度继续增加时,预测值与实验相差较大,主要原因是预测模型计算时沉陷度不变;而当床高大于0.7时,岩屑床已基本淹没钻杆,颗粒因沉陷度降低更易启动。如图7-B所示,临界流速预测绝对平均误差为2.51%。
当颗粒直径为1.4 mm时,临界流速预测值随无因次床面高度增加而增加。这主要是因为当钻井液排量增大时,即使流通区域减小,折算后所需临界流速也会增大(图8)。

图8 粒径=1.4 mm时临界流速预测值与PAC溶液实验值对比Fig.8 Comparison of the predicted value of critical flow velocity with the experimental data of PAC solution (particle size of 1.4 mm)(A)井斜角90°; (B)井斜角70°
当岩屑床孔隙较大时,床面高度对临界启动流速的影响较小,如岩屑直径为2 mm、3 mm时的实验和90°井斜角时的大颗粒(3~3.7 mm)实验数据可知,数据围绕某一流速值振荡,模型预测结果在岩屑床高度较大时趋于该流速值。
4 有效冲蚀岩屑床的钻井液临界排量
还可预测有效冲蚀岩屑床的临界泵排量,为现场优选水平井携屑排量提供理论指导。
设环空外圆与内圆半径的比值Ro/Ri=r*,则岩屑床上方流通区域横截面积表达式为
(32)
式中:λo为岩屑床面与井壁交点至井眼轴心处连线与竖直方向的夹角;λi为岩屑床面与钻杆交点至杆轴心处连线与竖直方向的夹角;h*为无因次床面高度;Af为流通区域截面积。
可以得到临界启动流速与泵排量间转换关系为
(33)
5 结 论
a.从床面颗粒表面绕流角度解析求解表面切力,当岩屑直径<3 mm时,可以用表面切力近似代替拖拽力。
b.当钻井液黏度较低且颗粒直径>3 mm时,计算拖拽力需要考虑压差阻力的影响。根据实验数据回归结果可知压差阻力约为表面切力的0.6倍。
c.当循环液为牛顿流体(清水)时,预测模型所得值最大绝对平均误差为8.80%;当循环液为非牛顿流体(PAC溶液)时,最大绝对平均误差为7.06%。
d.根据临界启动流速,可以求得保持冲蚀岩屑床的有效钻井液临界排量。
