基于新语言尺度函数的犹豫Z-number群决策模型*

姚爱婷，梅孔椿，毛军军，b，姚登宝

(安徽大学 a.数学科学学院; b.计算机智能与信号处理教育部重点实验室; c.经济学院，合肥 230601)

1 基本理论

群决策就是给定一组方案，对于每个方案有不同的属性，有多个专家对每种方案的属性做出评价。所做出的评价有很多类型，近年来有直观数字型、区间数型、语言型等，对不同类型的评价应用不同的决策模型从而选出最优方案[1]。1965年Zadeh提出模糊集(Fuzzy sets)理论[2]，模糊集在过去的几十年间已被广泛应用于统计决策、系统工程，模式识别等领域，现在被认为是决策问题、模糊推理和模式识别的有用工具[3-5]。Z-number是Zadeh[6]在2011年提出的概念，Z-number的构造试图把自然语言的客观信息显示和主观理解成分并列表达在一起，以便增强对自然语言的理解。

自Zadeh提出模糊集和Z-number的概念后，很多研究者以不同的角度对Z-number进行了研究，同时还提出了犹豫模糊集的相关理论。Torra and Narukawa[7]引入了犹豫模糊集(HFSs)，它允许元素的隶属度在[0，1]中成为一组可能的值，主要目的是在获取信息时对人类怀疑产生的不确定性进行建模。可是HFSs有一个不足之处就是这些经典模糊集合所提供的决策信息的可靠性并没有被充分考虑[8]；文献[9]分别从区间和单值两个角度研究直觉模糊集的多属性决策问题，并用规划模型解决了如何获取专家权重的问题；文献[10]利用偏好关系矩阵，从比较的观点研究了区间直觉模糊集的排序问题。

本文先介绍了语言型语集和语言型Z-number[11]，随后在三角函数的基础上引出两类语言尺度函数并证明了语言尺度函数的相关性质。在多属性群决策中，权重信息通常是不确定的，又由于决策者具有不同背景和个人偏好，因此不能直接赋予他们任意权重或相等权重，而由于时间的压力、问题的复杂性和缺乏知识的局限性，标准的权重也不应该根据经验值或主观的判断而分配。因此，对于一个实际的群决策问题，决策者的标准权重被认为是未知的并且要确定。本文的决策模型是在未知决策者属性权重的情形下建立模型确定合理的权重后进行决策排序的，由最后的实例分析可充分看出该方法的可行性和有效性。

2 基础知识

2.1 语言尺度函数

定义2[11]假设si∈S是一个语言型语集，即S={si|i=0，1，2，…，2t)}，假设现有一个数值变量θi∈[0，1]，设H是语言型语集si到θi的一个映射，即

H：si→θi(i=0，1，2，…，2t)

下面提出两类语言尺度函数(LSF)：

第Ⅰ类：

(1)

其中i=0，1，2，…，2t.

语言尺度函数LSF1具有以下性质：

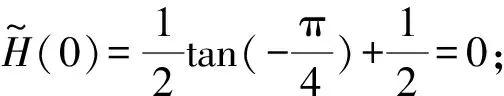
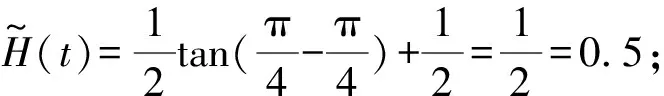
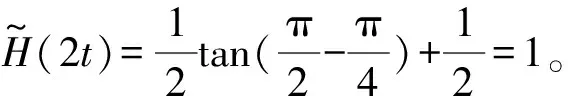
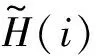
证明

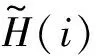
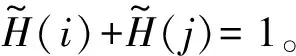
证明当i+j=2t时，有

语言尺度函数LSF2同理可证性质1、性质2和性质3。

第Ⅱ类：

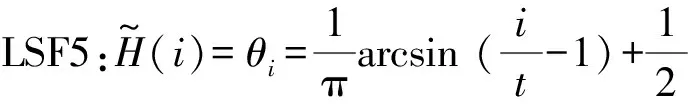
(2)

其中i=0，1，2，…，2t。

同第Ⅰ类语言尺度函数一样，也可以得到第Ⅱ类语言尺度函数同样有性质1、性质2、性质3。

语言尺度函数LSF1,LSF2,LSF3,LSF4,LSF5,LSF6的图形如图1所示：

图1 LSF1-6的函数图形

2.2 语言型Z-number

定义3[6]Z-number是有序的一对模糊数，表示为Z=(A，R)，第一个元素A是不确定变量X的实值函数，是对X在值上的约束；第二个元素R是对第一个元素A的可靠性的度量。当A，R都是语言型术语时，Z=(A，R)便是一个语言型Z-number。

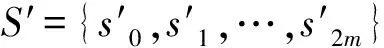
第一个元素Az(x)是X能够取值的一种模糊限制，第二个元素Bz(x)是对第一个元素Az(x)的一种可靠性的度量。一般来说，S和S′这两个语言型语集是不相同的，但它们都有明显的语言偏好信息。

3 犹豫语言型Z-number的距离公式

(3)

其中lφBi和lφBj分别是φBi和φBj的元素个数。

该距离公式充分考虑了两个语言型Z-number的不确定性，分别取两个语言型Z-number限制值的平均值，并对两语言型Z-number的区间上下界运算进行λ次方后开方，有效地缩小了语言型Z-number在反应数据信息过程中的犹豫不确定性。

4 基于犹豫语言型Z-number多属性群决策模型

第1步令E={E1，E2，…，Ep}为多个决策专家集合，X={x1，x2，…，xn}为方案集合，C={c1，c2，…，cm}为属性集合，W={w1，w2，…，wm}为已知属性权重集合。

第3步由距离公式(3)计算每两位决策专家对同一方案属性的决策距离，并写出决策距离矩阵。

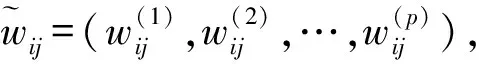
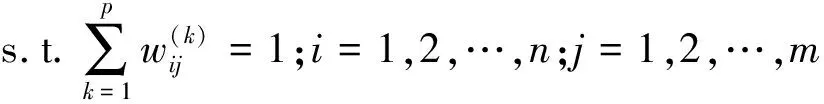
(4)

第6步计算可能度。先利用IWAA算子对综合矩阵的每个方案xi属性aj计算得到综合属性值：

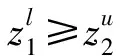
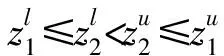
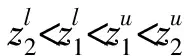
第7步由第5步得到的可能度矩阵是一个模糊互判矩阵，根据模糊互判矩阵排序理论的排序公式：

i=1，2，…，n

(5)

得到可能度矩阵的排序向量v=(v1，v2，…，vn)，并按其分量的大小进行排序得到最优决策方案。

5 实例分析

本文以一个实例分析来展示模型应用，现有决策者E1，E2，E3，某供应链核心企业拟选择一个伙伴企业进行合作，共有4个备选伙伴企业(方案)xi(i=1，2，3，4)可供选择，决策者利用语言评估标度S={s1，s2，…，s8}={很差，差，较差，一般，稍好，较好，好，很好}对备选伙伴的4个关键因素(供应时间与能力、质量与技术水平、价格与成本、服务水平)cj(j=1，2，3，4)做出决策。

第1步令E={E1，E2，E3}为3个决策专家集合，X={x1，x2，x3，x4}为方案集合，C={c1，c2，c3，c4}为属性集合，W={w1，w2，w3，w4}为已知属性权重集合，表1，2，3为专家E1，E2，E3的决策矩阵。

第2步将表1，2，3的决策矩阵用式(1)和式(2)两个不同的语言尺度函数数字化后得到语言尺度值矩阵Ek=(eij)n×m，以专家E1为例(表4)。

第3步由距离公式(3)计算每两位决策专家对同一方案属性的决策距离，有以下决策距离矩阵：

D(E1，E2)=D(E2，E1)=

D(E1，E3)=D(E3，E1)=

D(E2，E3)=D(E3，E2)=

表1 专家E1的语言型决策矩阵

表2 专家E2的语言型决策矩阵

表3 专家E3的语言型决策矩阵

表4 专家E1的语言尺度值矩阵

得到专家在不同方案不同属性下的权重：

第5步综合矩阵

第7步由式(5)得可能度P矩阵的排序向量

v={0.255 9，0.257 4，0.218 9，0.215 0}

所以这4个方案的排序为x2>x1>x3>x4，即第2个企业为最优选择。

6 结束语

本篇论文结合Z-number理论和语言型语集提出了两类新的语言尺度函数并定义两个不同的犹豫语言型Z-number之间的距离。利用新的语言尺度函数和距离公式,结合集成算子理论建立了未知专家属性权重的群决策模型，从理论方面计算出了合理的专家属性权重后,结合集成算子理论利用区间数的算术平均将决策矩阵集成为综合矩阵，通过建立二维的可能度比较可能度矩阵，然后利用排序向量法进行决策排序得到最优方案。该模型充分考虑了多位专家不同背景和个人偏好等因素在群决策中的不确定性，减小了数据信息不确定性造成的影响，从而提供了更直观、准确的信息。