某软岩隧道变形规律和二衬最佳支护时机选择研究

李贤，蔡林真

(1.云南省交通规划设计研究院有限公司, 云南 昆明 650051；2.云南公路工程检测有限公司)

相较硬岩隧道围岩-支护体系，软岩隧道的支护-围岩系统的服役性能变化规则更加复杂，这种特性在大断面-软岩隧道中更加明显。隧道二次衬砌最佳支护时机选取更为重要。

孙钧等学者于20世纪末通过大量试验推导出了剪切应变控制理论，并得到最佳支护时机选取的试验公式；KAISER P K等运用试验方法对隧道施工各个过程中围岩应力、变形及衬砌内部应力-形变的时间-空间变化规则进行研究，结果表明部分岩性及支护具有流变特性；岩石流变性是岩石较为重要的力学特性之一，对岩体应力-应变特点的时间-空间效应有重大影响，而工程的失稳或破坏往往是有时间过程的；王中文等利用围岩变形现场监测数据，结合回归分析，得出了不同围岩情况的流变特征参数，给出了不同初期支护强度和不同断面尺寸隧道的二次衬砌合理支护时机；周勇等为了得出考虑围岩流变特性情形下的二次衬砌的最优支护时机，率先给出了考虑岩石流变特征的衬砌应力、应变及围岩的位移-时间-空间规律，并在此基础上给出了特定条件下的隧道二次衬砌最佳支护时机的计算方法，并对变形监测实测值和数值计算值进行了较为全面的对比。研究大断面大变形软岩隧道的二次衬砌支护时机具有重大的现实意义，但由于隧道工程地质条件的复杂性和隐蔽性，二次衬砌最佳支护时机的选取仍然是工程界的重点和难点。

针对这一工程难点问题，该文以某泥岩大断面隧道为工程背景，针对软弱泥岩大断面隧道的二次衬砌支护时机进行研究。通过考虑岩体蠕变特性的理论计算和现场围岩形变的监控量测数据的回归分析，辅以公路隧道相关规范得出该隧道的围岩变形规律和确定二次衬砌的最佳支护时机。

1 工程概况

该隧道右幅起迄里程：K0+755～K1+775，隧道总长1 020 m；全隧道位于直线上；隧道的最大埋深约132.6 m。该隧道左幅起迄里程：ZK0+740～ZK1+760，分界段全长1 020 m；隧道最大埋深约122.8 m。

隧址区围岩岩性主要为全～强风化，中等风化泥岩，砂岩，地表覆盖层较厚，多为第四系坡积、残积土，降雨量集中在6—9月，地表植被稀疏。

2 考虑岩体蠕变特性的围岩变形规律及衬砌最佳支护时机理论分析

2.1 蠕变作用下隧道位移公式

当考虑隧道围岩的蠕变效应时，隧道衬砌抗力p0、位移uccrep公式为：

(1)

(2)

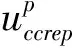
(3)

式中：

k=3-4u，kc=3-4uc。

式中：u为开挖隧道围岩泊松比；uc为围岩初支泊松比；r0为隧道轮廓半径；r1为隧道初支半径；R0为塑性区半径；Gc为初始剪切模量；G0为中期剪切模量；G∞为最终剪切模量；α为流变参数；t为时间；r为隧道开挖轮廓的等效半径或等效初支内半径。

在隧道开挖后，初期支护所抵抗的位移变形utt为：

(4)

将式(1)、(2)、(3)代入式(4)，可以得到：

(5)

由于在大断面软岩隧道的条件下，式(5)所计算的初期支护最终位移值，没有考虑由于掌子面开挖而引起的前方拱顶的前期下沉值，并且这一部分下沉值是无法通过监控量测得到的。这里依据张顶立等的研究成果，在软弱围岩地质条件下，围岩变形，特别是竖直方向上的开挖前沉降量约为终期总位移量的40%，该部分沉降对判定二次衬砌最佳支护时机的选取有着重大影响。即可得出初期支护的最终位移变形量为utt′：

(6)

式(2)中：G∞，α，r0为未知项，其余可以由现有资料确定，G∞，α，r0通过工地监控量测得到数据后进行数学回归分析可得。式(2)中提出的假定条件隧道为圆形，则可以通过式(7)进行等效替换。例如三心圆、马蹄形等。

(7)

式中：h为隧道高度;B为轮廓跨度或初期支护内跨度的一半。

2.2 隧道围岩变形规律分析

根据现场地质调查追踪发现，该隧道的围岩强度低；风化程度较高；多为中厚层状～薄层状结构，节理裂隙多为发育～很发育，呈无序状；岩体自稳能力弱，累积沉降大，开挖初期阶段位移速率快，开挖后会产生较大的蠕变变形，具有较为明显的时间-空间效应。

3 隧道围岩变形现场监测

3.1 现场监控量测

在该隧道施工过程中按照隧道监控量测相关规范进行了围岩变形监测断面和监测点的布置，现场测点布置如图1所示。

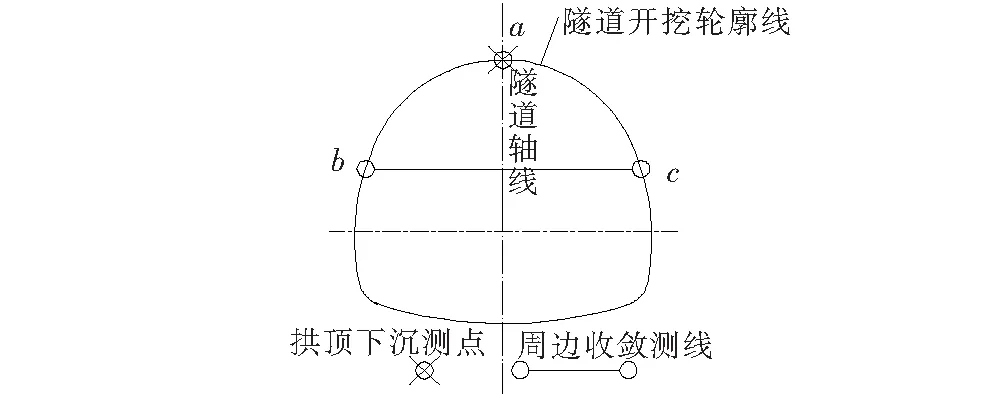
图1 现场测点布置图

3.2 选取计算断面

选择断面ZK1+050、ZK1+060、ZK1+070、ZK1+080的现场监控量测数据进行计算，选择断面所处围岩区段为ZK0+770～ZK1+130段，量测断面和高密度电法的预报结果如图2所示。

通过对高密度电法的图形进行解译可以得出：

ZK0+770～ZK1+130段：视电阻率大多小于300 Ω·m。结合设计图纸，推测围岩为强风化泥岩，节理裂隙发育，岩体呈块碎～碎石状压碎结构，地下水较丰富，围岩稳定性差。开挖后不及时支护拱顶易发生坍塌、侧壁失稳，围岩级别推定为Ⅴ级。

3.3 监控量测数据分析

考虑蠕变因素，隧道围岩位移-时间变形规律采用式(8)进行拟合：

Y=a+be-kt

(8)

式中：a,b,k为回归函数拟合参数；t为时间。

通过Origin8.0进行回归分析可得拟合参数如表1所示。

各围岩变形监测断面拱顶下沉位移-时间的散点图以及回归曲线分别如图3、4所示。

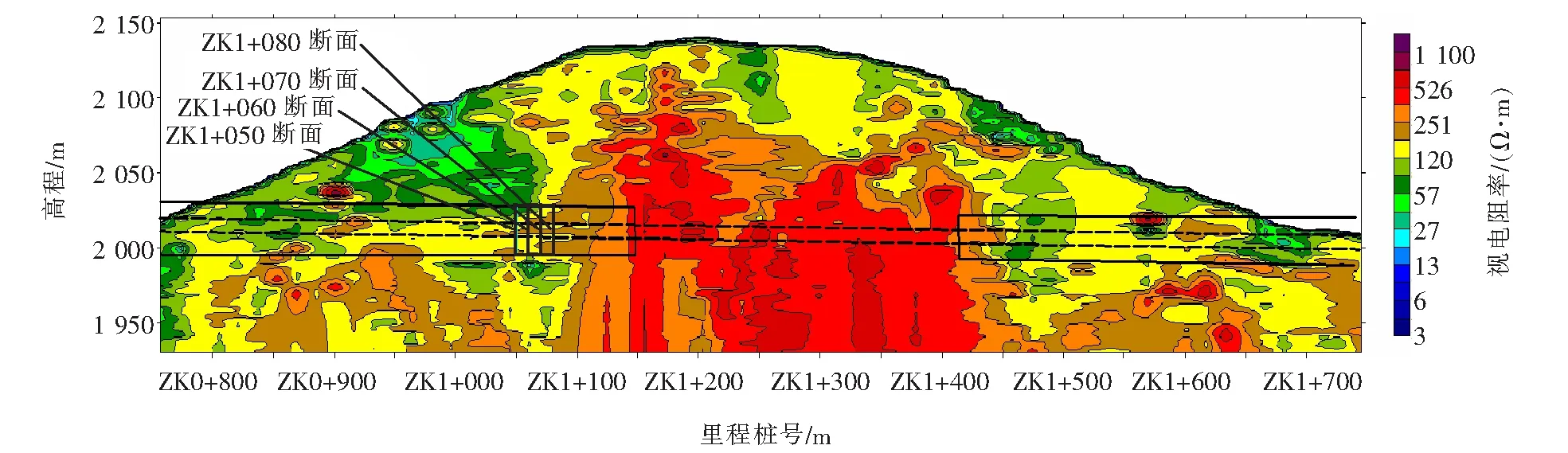
图2 左幅高密度电法测试结果视电阻率成像图

表1 隧道拱顶下沉和周边收敛回归分析统计

注：R2为拟合曲线的相关系数。

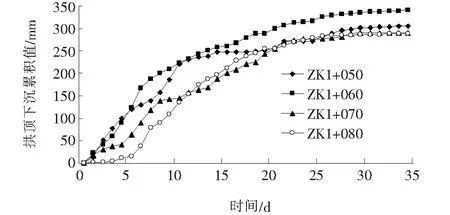
图3 各量测断面拱顶下沉位移-时间回归分析曲线图

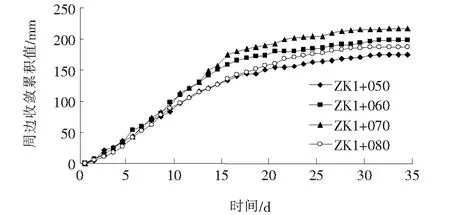
图4 各量测断面周边收敛位移-时间回归分析曲线图

拱顶下沉(UV)和周边收敛(UH)位移公式分别如式(9)、(10)所示：

UV=332.55-378.68e-0.077t

(9)

UH=222.78-258.53e-0.073t

(10)

3.4 隧道二衬最佳支护时机

根据JTG F60-2009《公路隧道施工技术规范》相关规定，结合隧道现场监测情况，该隧道Ⅴ级围岩段取最终围岩变形的80%作为二衬最佳支护时机。

当t→+∞时，UV=332.55 mm，UH=222.78 mm，80%UV=266.04 mm,80%UH=178.22 mm。

根据对该隧道现场施工进度进行调查可以得出隧道开挖进尺的情况，在这里参考围岩的变形速率进行分析，结果如图5、6所示。

通过Origin8.0进行线性回归分析，可以得出二次衬砌距掌子面的距离(L)与时间(t)的函数关系为：

L=3.75+1.55t

(11)

相关系数R2=0.976 6。

则最佳支护时机的选择结果如表2所示。

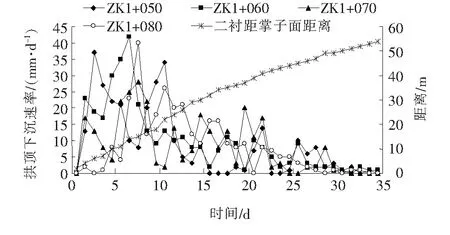
图5 各量测断面拱顶下沉速率-时间及掌子面与二衬距离图

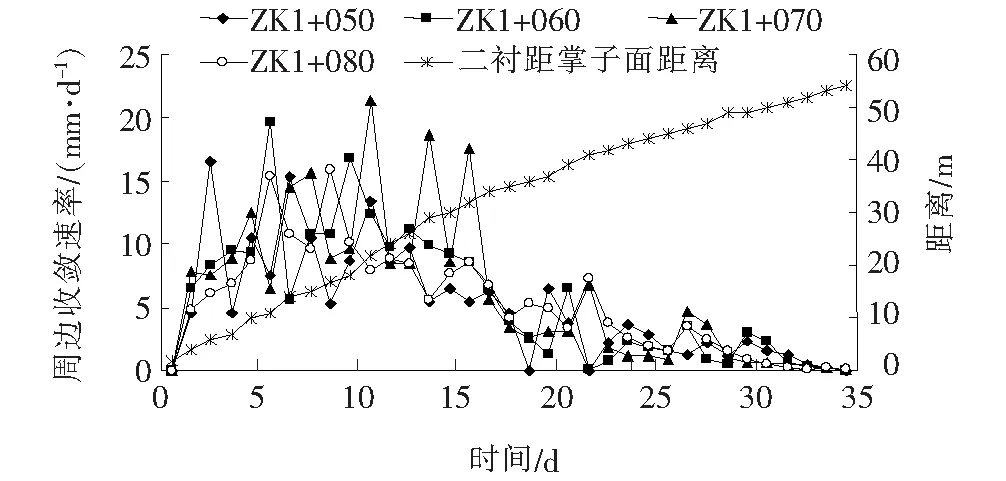
图6 量测断面周边收敛速率-时间及掌子面与二衬距离图

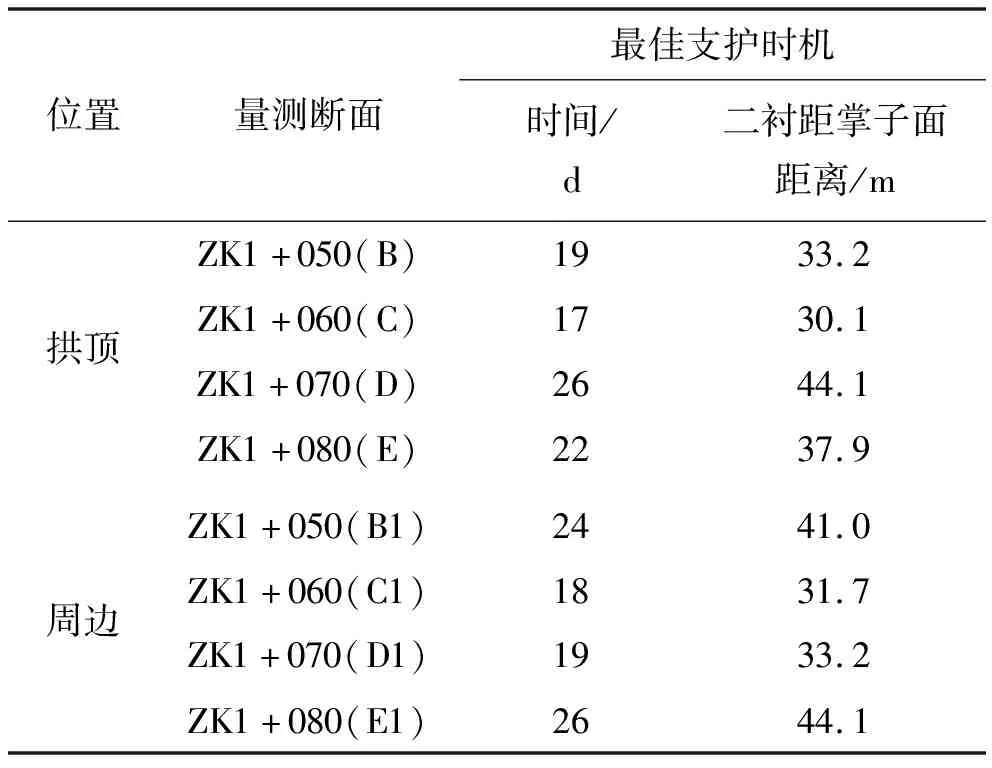
表2 该隧道不同段落二次衬砌最佳支护时机统计

4 结论

(1)隧道二次衬砌作为隧道结构物的安全储备，为使隧道有较为充足的安全储备，有两种方法：① 加强初支支护强度；② 充分发挥围岩的自承能力。然而加强初期支护会增加施工成本，不经济，因而选择一个合理的二次衬砌支护时机更加经济合理。

(2)以具体隧道为工程背景，进行了考虑围岩蠕变的位移理论计算、完成了现场监控量测数据的回归分析，对该隧道Ⅴ级围岩段的二次衬砌最佳支护时机(段)进行了定量分析，即：17～26 d为该隧道Ⅴ级围岩段的最佳支护时段，而二次衬砌最佳支护距离为距掌子面30.1～44.1 m。支护时机可根据围岩变形稳定状况作调整，若变形-稳定周期较长，则二次衬砌支护时机取较大值；若隧道围岩变形至稳定的周期较短，则可稍微提早施作二次衬砌。

(3)该文所采用的考虑围岩蠕变的位移-时间关系函数没能考虑地下水的影响，仍需进一步完善。