变高围墙锥坡在桥梁中的应用

葛占钊

(吉林省交通规划设计院，吉林 长春 130021)

1 引言

随着国民经济的快速发展，交通量迅速增加，基础设施投入也越来越大。目前中国还有大量的道路需要新建或改扩建，这些项目中包含很多桥梁需要修建；另外随着设计理念的改变和技术水平的提高，“安全、环保、舒适、和谐”的设计理念更加被重视，因此外形美观、设计节能环保的设计理念逐渐被重视，贯穿至桥梁设计的每个环节。

锥坡(图1)虽然看似桥梁的次要结构，设计中常常不被重视，但其作用是不可忽视的，作用之一是解决路基与桥梁结构连接问题(主要挡土作用)；其二是解决导流问题，使水流顺畅，减少冲刷。另外外形美观也是设计中应该考虑的因素之一。

图1 锥坡

该文主要针对通道、小桥椭圆锥坡围挡墙样式进行改进设计，给出计算方法，并实现程序化出图，提高设计效率，解决施工技术难题，因此对实际设计、施工具有一定的指导意义。

2 桥梁常用锥坡样式

桥梁锥坡的样式较多，常用的结构形式主要是椭圆锥坡和八字墙锥坡，从水力学的观点来看：能迅速宣泄水流，使河滩及河床的水流、流速能够合理分布，流量能够分配均匀、顺畅而平稳地从上游通过桥孔流向下游，在桥下不产生漩涡而冲刷均匀，符合水流天然状况并与客观情况相适应的最有利形式，是洞口的八字墙在平面上有流线形的式样。也就是说，洞口八字翼墙，最好具有曲线形，以采用椭圆形底面椎体为宜，故采用椭圆锥坡较为合理。另外采用椭圆锥坡，不但能使水流通畅与流量均布，而且还能节省台身混凝土用量，保护与简化桥台构造，降低造价。

锥坡坡脚线产生椭圆形是由于锥坡在路基方向连接路堤边坡坡度与前坡的坡度采用不同的坡比或者桥梁有一定交角造成的(交角90°且等坡时为圆形)。所以两坡度在底平面上的投影线就长短不一，最终形成了椭圆的长短半径，只有采用椭圆形才能使坡脚线平滑连接(处处相切)。

现行设计中通道、小桥的锥坡常采用等高围墙+变高挡墙的形式(图2)，此种形式锥坡外观不是很美观且混凝土用量较大，不够经济、也不节能环保。

通过研究，将原有通道、小桥的锥坡样式进行改进，将围墙改为变高度围墙，末端直接放至边坡坡脚，去掉挡墙部分，形成一种新的锥坡样式，并已在吉林省内高速公路上大量应用，此种形式锥坡外型美观且混凝土用量较少，经济性比较好。

图2 围挡墙锥坡

3 变高围墙锥坡的设计思想

3.1 椭圆锥坡的计算方法

正桥与斜桥的桥台两侧的椭圆锥坡，从外形上看是不相同的。底面：正桥锥坡是正椭圆弧、正椭圆锥面；斜桥锥坡是斜椭圆扇形面。外缘曲线是斜椭圆弧。事实上斜桥的4个斜形锥坡的底面积与椭圆弧曲线组合在一起，与正桥的4个正形锥坡底面积和椭圆弧连成的正椭圆面和椭圆周是统一的，斜椭圆即寓于正椭圆之中。因此通过计算正斜椭圆长短半径及正椭圆长半径与斜椭圆共轭长半径夹角，即可绘制相应的锥坡坡脚线，计算公式如下(部分参数示意见图3)：

K1=M/cos(π/2-φ)

(1)

(2)

(3)

K4根据工程实际情况确定，一般不小于1.0。

AR=K3×H

(4)

BR=K4×H

(5)

α=K1×H

(6)

β=K2×H

(7)

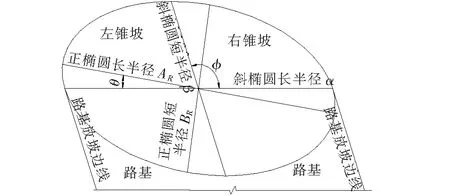
图3 锥坡参数示意图

(8)

式中：K1为斜椭圆长半径的锥坡面坡度；K2为斜椭圆短半径的锥坡面坡度；K3为正椭圆长半径的锥坡面坡度；K4为正椭圆短半径的锥坡面坡度(斜锥坡坡面最陡坡度值)；M为路基边坡坡度(一般为1∶1.5)；H为锥坡高度；AR为正椭圆长半径；BR为正椭圆短半径；α为斜椭圆共轭长半径；β为斜椭圆共轭短半径；θ为正椭圆长半径与斜椭圆共轭长半径夹角；φ为桥梁斜交角。

通过计算推导出的正椭圆长、短半径和正椭圆长半径与斜椭圆共轭长半径夹角来绘制锥坡坡脚线，并计算锥坡工程量，进行施工放样。

3.2 变高围墙椭圆锥坡计算

变高围墙锥坡和等高围挡墙锥坡不同之处是起、终点围墙高度不同，无法完全利用标准椭圆锥坡的计算公式解决，需要转化，故计算椭圆锥坡时会引入两个高度h1和h(图4、5)，先根据路基边坡M、斜椭圆短轴半径β(根据耳墙长度计算，定值)及桥梁斜交角度φ，由式(1)、(2)计算出K1、K2，再由式(7)求出围墙起点锥坡高h1，引入已知末端锥坡高h，由式(6)计算斜椭圆长轴α，将椭圆锥坡转化为统一的假定锥坡高度h进行反算最陡坡及相关参数，即由式(7)求出新K2=β/h(仅计算用)，之后由式(2)推导出新的K4(坡脚斜锥坡坡面最陡坡度值)：

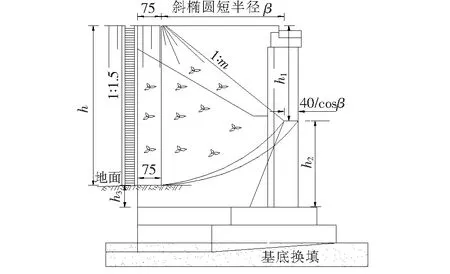
图4 锥坡立面示意图(单位：cm)

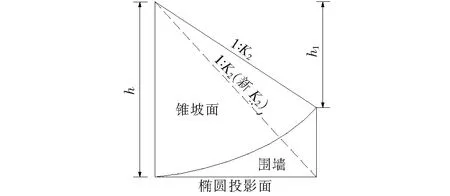
图5 椭圆锥坡转换计算示意图

K4=

(9)

再由式(3)求出K3，即可求出相应的正椭圆长、短半径及正椭圆长半径与斜椭圆共轭长半径夹角θ，从而绘出椭圆锥坡围墙线形，使变高围墙锥坡问题得到解决。

3.3 变高围墙椭圆锥坡工程量计算

锥坡铺砌面积计算：可以根据积分原理，应用编程方式，通过对弧长微分,将表面化成小的扇形(图6)，再近似等效为三角形，从而通过求a点到b点弧长上积分的小三角形面积之和的方式，求出锥体表面积，即可得到铺砌的面积。

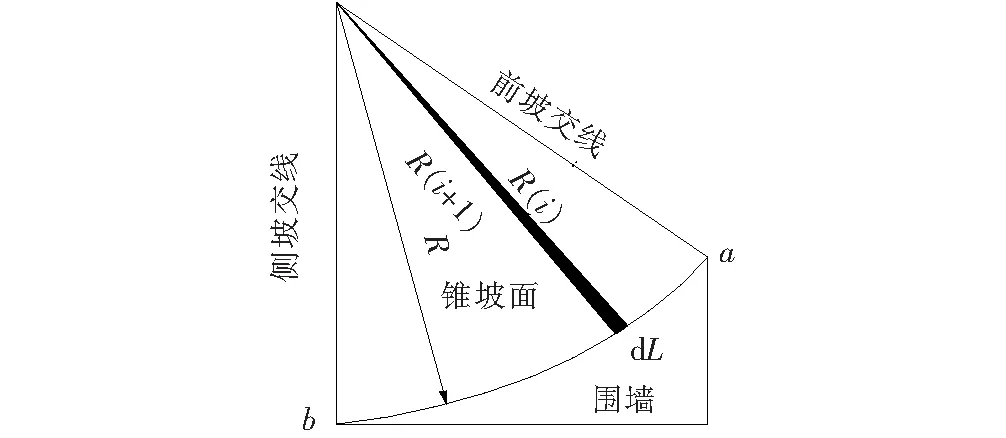
图6 椭圆锥坡表面微元划分

而锥体填土体积、围墙体积、围墙基础体积可采用同样方法处理，通过编程方式逐个计算出锥坡工程量，从而解决所有锥坡工程量计算问题。

4 变高围墙锥坡施工放样的计算方法

4.1 计算原理

修建变高锥坡围墙的难点是施工时不仅要控制每点的平面位置，同时也要控制挡墙的高度变化，为了解决这个难题，经过多次探讨拟采用极坐标的处理方法，此种方法会得到很好的处理效果，并且方便施工放样。具体做法是以锥坡轴线与围墙底面交点为坐标原点、以耳墙边线为极坐标轴建立极坐标系(图7)。

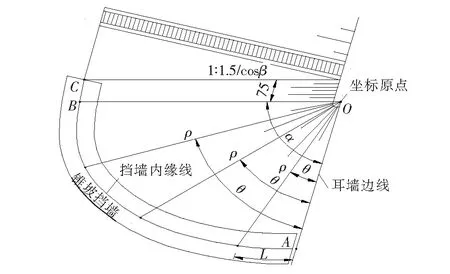
图7 锥坡极坐标示意图

建立坐标系后，应用该文中变高围墙椭圆锥坡计算方法计算出锥坡椭圆参数，再设定围墙的分段数，该文按10段处理(可以任意分段，分段越多越精细)，共11个点，计算中分别给出围墙弧长L、极半径ρ、转角θ和对应位置的墙高h(表1)，这些参数可直接用于施工放样，从而降低了施工放样的难度，提高了效率。

4.2 变高围墙锥坡程序研发与应用

根据以上分析内容，可以看出锥坡计算的工程量较大，因此必须采用编程方式解决，拟采用vb.net调用windows系统.NET Framework 4.0框架进行程序开发，并调用AutoCAD形成可视化快速绘图程序，此程序界面友好，简单易用。使用该程序可以转化纬地数据文件(也可以自己编辑数据)，填写基础数据后，自动调用平、纵、横数据，计算高程及各参数，计算放样坐标数据及工程量，并自动绘制锥坡图纸，其中包括变高围墙锥坡各控制点高程，结构尺寸、椭圆参数，围墙放样极坐标等。

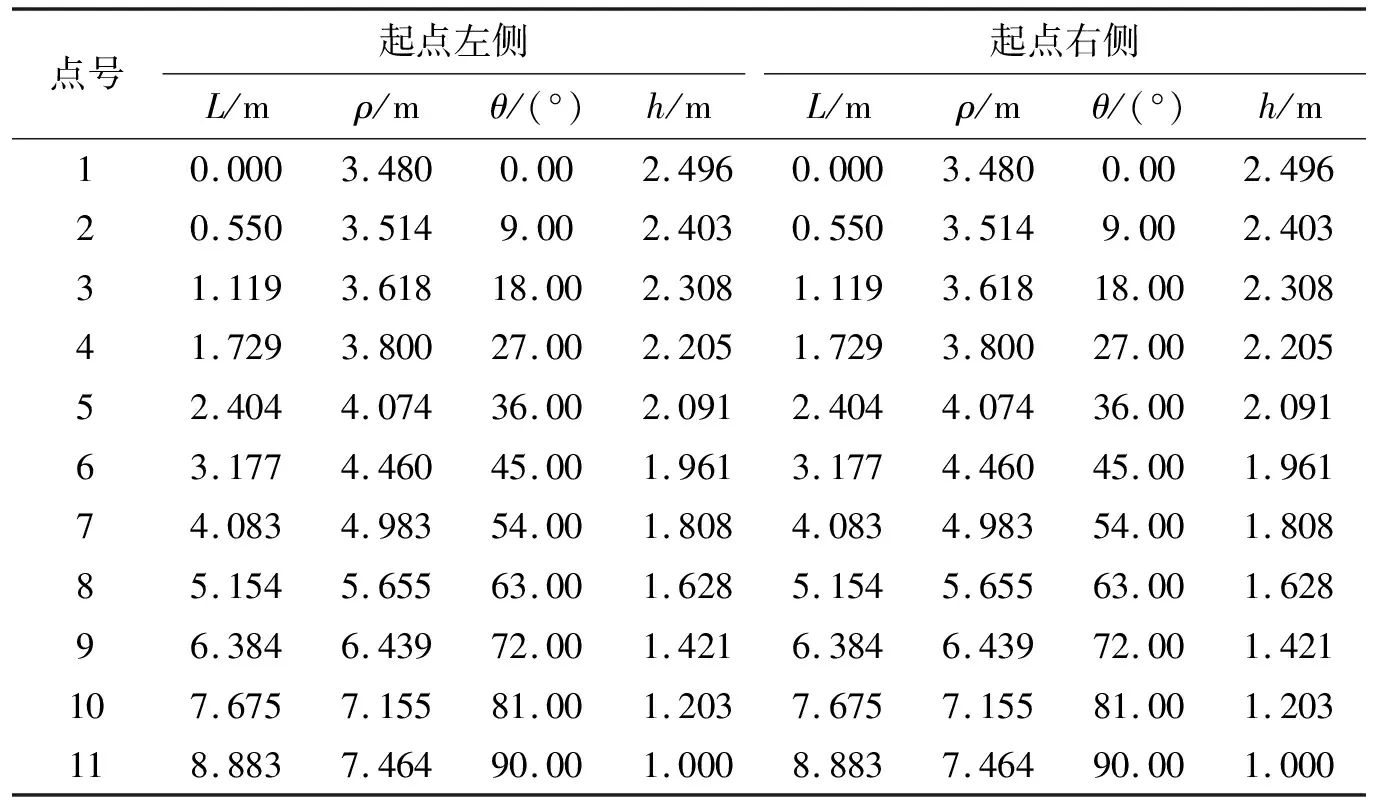
表1 围墙锥坡坐标

此种改进的变高围墙锥坡已在吉林省内各条高速公路建设中广泛使用，有的高速已经建成通车(如京哈高速长平段改扩建工程、鹤大高速、长春至双辽高速等)，并且取得了很好的效果，降低了工程造价，增加了整体美观程度。

5 结论

(1)采用新型变高围墙锥坡防护结构可以使桥梁整体更加美观、协调；有利于桥下排水，使水流顺畅，减少冲刷；可以减少混凝土用量，降低工程造价。

(2)采用编程开发出图，生成极坐标控制数据，有利于后期施工放样，降低施工难度。

(3)该文变高围墙锥坡形式也可应用于大中桥收坡脚、前坡设一定高度挡墙的桥梁中，可扩展应用范围较强。