三轴压缩加载频率对花岗岩疲劳特性影响试验
2019-04-16黄正均赵星光蔡美峰任奋华郭奇峰
黄正均,赵星光,蔡美峰,任奋华,郭奇峰
(1.北京科技大学土木与资源工程学院,北京 100083; 2.核工业北京地质研究院,北京 100029; 3.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京 100083)
岩石具有不连续、不均质、各向异性等特点,其力学行为和变形特性与岩性、受力条件、环境等诸多因素相关[1]。其中,岩石受动态循环荷载作用时的力学特性又尤为复杂,近年来也受到众多学者们的广泛关注,即所谓“岩石疲劳”。因此,研究不同岩石的疲劳特性,并采用合适方法对其损伤演化机制进行描述,对采矿、水利、交通等岩土工程中评价岩体长期稳定性,以及指导工程设计、施工具有显著影响[2-3]。
根据现有研究基础可知,疲劳荷载作用下,岩石破坏特征与施加应力上限、振幅、围压以及频率等因素密切相关[4-6]。国内部分学者[7-9]通过大理岩和砂岩等在单轴时的疲劳压缩试验,重点研究了弹模、形变和声发射特征在疲劳过程中的变化规律,同时还揭示了上限应力、振幅等对疲劳特性的影响。国外部分学者[10-12]也研究了围压和频率对砂岩在动态疲劳压缩下损伤特性的影响,提出岩样破坏时的轴向应变和开始膨胀时的残余体积应变随围压呈同步增大;破坏时的加载次数和膨胀开始时的残余体积应变呈随频率增加而增大的规律,另外还采用不同方法描述了岩石的损伤演化过程。
上述成果主要针对砂岩、大理岩等进行了较多试验研究,对花岗岩的研究以单轴条件下的疲劳特性居多,而对三轴压缩下各因素对花岗岩变形、损伤发展及疲劳寿命影响方面却甚为少见。因此,本文选取均一性好的花岗岩为研究对象,通过开展三轴压缩下的动态疲劳试验,探讨加载频率对岩石疲劳特征和损伤演化的影响,为后续与花岗岩相关的地下硐室掘进、采矿凿岩破碎等提供基础数据。
1 试验设备及方案
1.1 试验用岩石样品
本次选取甘肃北山的花岗岩作为试样,取样深度为440~450 m。根据前期薄片鉴定结果,岩石的主要矿物成分为石英、斜长石和黑云母等,并被定名为中细粒二长花岗岩。通过基本物性试验得出,岩样的平均密度、纵波波速和动弹模分别为2.643 g/cm3、4 159 m/s和45.73 GPa。试验共选取了6件标准岩样,尺寸为50 mm×100 mm,加工精度满足ASTM、ISRM、国家标准等试验方法和标准要求。
1.2 加载设备
本次试验主要在岩石动态力学测试系统(MTS 815)平台上进行。该设备具备轴向可加载最大载荷2 700 kN、围压最大140 MPa、循环加载振动频率、0.01~5 Hz等功能参数。同时,采用一套最大量程分别为5 mm和8 mm的岩石变形测量引伸计,用以测量岩样压缩过程中的轴向和环向变形。此外,试样外部采用3M热缩管进行防油处理,两端涂有凡士林以减小端部摩擦效应的影响。
1.3 试验加载方案
本次试验主要考虑轴向加载频率作为影响因素进行试验设计,试验全程在三轴压缩条件下进行,并将加载过程分为静态加载和动态疲劳两段。图1为试验设计的应力加载路径。首先,静态加载阶段,先以应力控制加载方式(速度0.1 MPa/s),施加围压至预设值5 MPa;随后切换为环向变形控制方式,进行轴向加载(速度0.025 mm/min)。环向变形控制为岩石刚性试验最常采用的加载控制方式,它可有效控制岩样在接近峰值强度时不会发生突然破坏的可能。
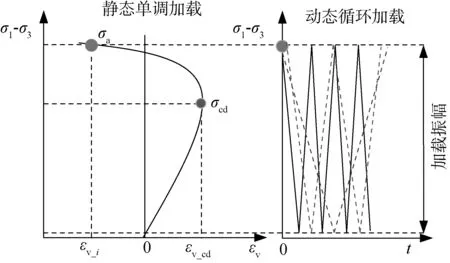
图1 试验设计的应力加载方案Fig.1 Stress loading scheme of experimental design
进行静态加载的同时,实时监测岩样加载过程的偏应力σ1-σ3——体积应变εv曲线,并记录岩样的裂隙损伤应力σcd和对应的体积应变εv_cd值继续加载直至体积应变达到预设目标值εv_i时,立即以正弦波形式开始第二段的动态疲劳加载直至岩样发生破坏[13]。疲劳加载方案采用围压固定(5 MPa),轴向动态加卸载的方式进行,加载上下限分别为590 kN和20 kN,即幅值为570 kN。
2 试验结果及分析
2.1 疲劳特征分析
岩石疲劳特征与频率、载荷等多种因素有关,本文主要考虑不同加载频率条件下,其疲劳特征参数和损伤的变化规律。根据上述试验加载方案,共完成了6件不同频率下的花岗岩动态疲劳加卸载试验。部分岩样加载过程的应力-应变曲线如图2所示,表1列出了全部岩样在试验过程所获得的部分特征力学参数。
由表1分析可知,所有岩样的加载频率在0.1~2.0 Hz不等,但其裂隙损伤应力σcd基本一致,除BS06-2试样偏小外,其余差异小于8 MPa,对应体积应变基本在0.15%~0.16%附近,其标准差SD值和变异系数CV值分别小于3.5 MPa、0.005%和1.5%、3.4%,表明试验选用岩样的一致性好,为后续试验分析提供了有效、可靠的样品保障。然而,虽然各岩样的加载频率不同,但其余条件一致,其破坏时的加载次数却各不相同,在295~1 763 次不等。
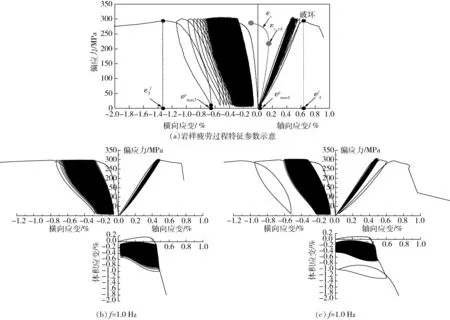
图2 不同频率下部分岩样的应力-应变曲线Fig.2 Stress-strain curves of some rock samples at different frequencies
表1 岩样在动态循环加载条件下的特征参数Table 1 Characteristics parameters of rock samples under dynamic cyclic loading conditions

岩样编号fσcd/MPaεv_cd/%εv_i/%εf1/%εf3/%εpmax1/%εpmax3/%NfBS14-40.1223.660.160-0.10.501-0.7970.030-0.275296BS09-30.25222.130.148-0.10.548-0.746-0.105-0.270295BS14-60.5216.070.154-0.10.590-0.5600.146-0.611303BS06-21.0200.130.090-0.10.503-0.6020.035-0.525501BS07-41.5216.510.151-0.10.608-0.758-0.175-0.372730BS16-12.0216.630.162-0.10.508-0.7060.101-0.4821 763
注:f为动态加载频率,其余参数定义参照文献[14]
从图2可知,无论是轴向应变还是横向应变,岩石疲劳过程中的应力-应变曲线均可根据曲线特征,分为“疏-密-疏”三种不同发展阶段。与此相应,疲劳过程中岩石损伤演化同样可分为“初始发展”“稳定发展”“快速增长”三个阶段。显然,岩石在疲劳变形发展的各阶段中,轴向应变发展速度明显缓于横向应变,进一步证实了本文作者前期研究成果所得论点,即侧向膨胀对岩石疲劳变形发展起主导作用[17-18]。
2.2 加载频率对疲劳特征参数的影响规律

图4为不同轴向加载频率下,各岩样疲劳特征力学参数随加载过程的变化曲线。其中,图4(a)为岩样的弹性模量与加载次数的关系。从图4可知,随加载次数增加,岩石弹性模量呈非线性减小趋势,与体积应变、横向应变规律相似,均呈“倒S”型曲线。各岩样疲劳加载初始时的模量分别为69.15 GPa、71.37 GPa、68.68 GPa、67.32 GPa、67.96 GPa、70.32 GPa,标准差为1.37 GPa,表明岩样的初始刚度较为一致,岩性均一。但最后一次加载段的模量分别为59.77 GPa、57.68 GPa、30.10 GPa、46.21 GPa、48.32 GPa、42.43 GPa,差异较大,且不受频率变化明显影响。图4(b)为岩样峰值横向应变随加载次数的变化曲线,其规律与弹性模量变化曲线基本一致,呈“倒S”型,初始横向应变除BS06-2试样(f=2.0 Hz)外,均相差不大。最后一次加载时,横向应变均随频率增大呈现先大再小的变化规律,表明岩样的横向膨胀受频率影响较为明显。当频率越高时,岩样的横向膨胀未来得及全部实现,应力便已释放,故其累积膨胀量越小。

图3 破坏瞬时应变和最大塑性应变-频率关系Fig.3 Relationship of destruction instantaneous strain and maximum plastic strain and frequency
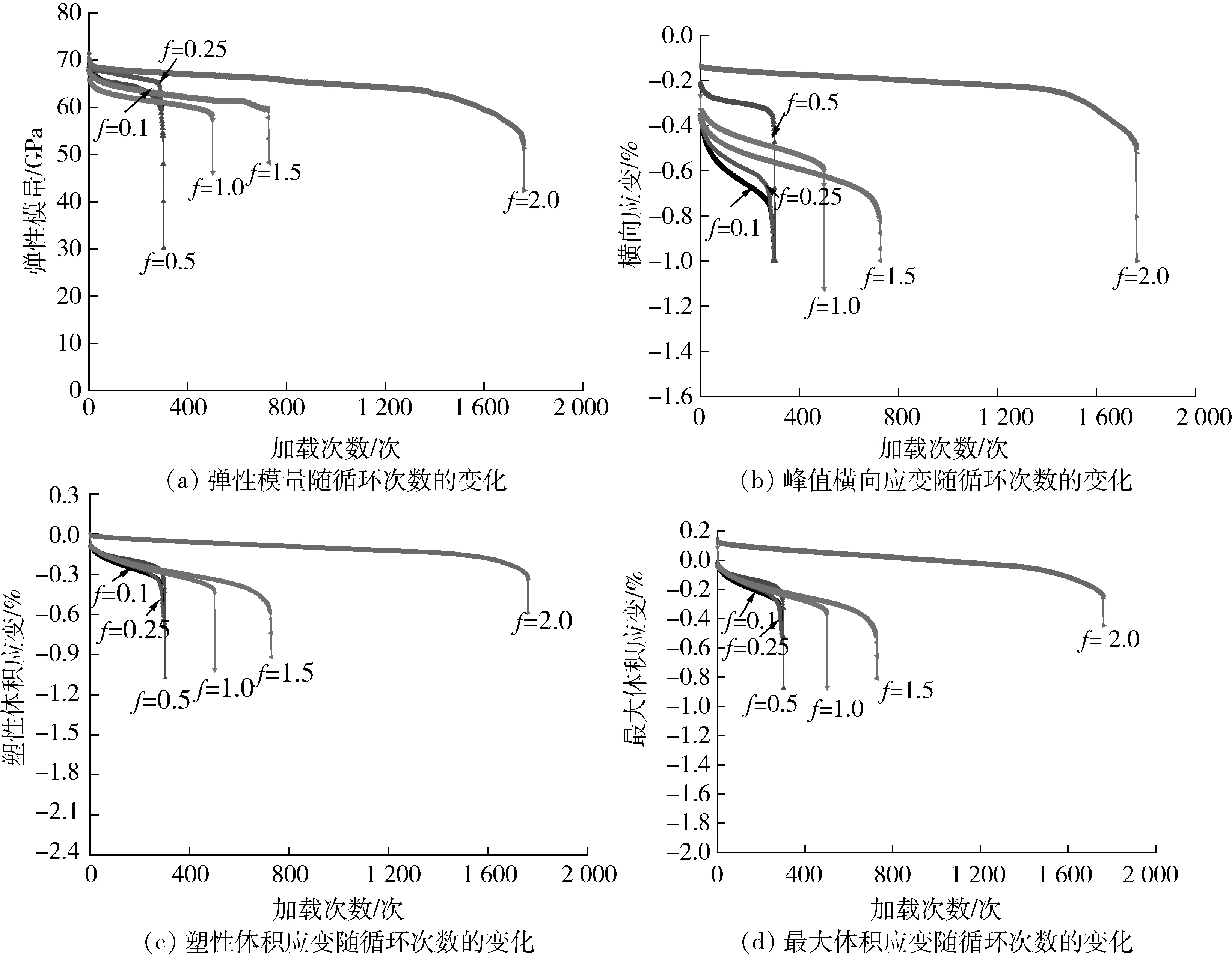
图4 不同频率下疲劳特征参数随循环次数关系Fig.4 Relationship between fatigue characteristic parameters and cycle times under different frequencies
通常,以体积应变(εv=ε1+2ε3)来表征描述岩石的变形损伤过程。图4(c)和图4(d)分别为岩样塑性体积应变和最大体积应变随加载次数的关系。从中可知,其曲线变化规律几乎一致,同样呈“倒S”型,但前期加速变形阶段随频率增大而变短,表明频率越大,加载对岩样造成的损伤发展过程越短。同时,频率愈大,稳定变形阶段的持续次数愈多,表明岩样抗载荷冲击破坏能力愈强。岩样疲劳加载初始时的体积应变不影响破坏时的应变,最后一次加载时的最大体积应变和塑性体积应变均随频率呈先大后小趋势,与前述横向应变的影响规律一致,更加明确了岩样疲劳损伤过程的主导因素为侧向膨胀而非轴向压致裂。
从图4还可以看出,在变形稳定发展阶段,岩样的弹模衰减率、横向应变率和体积应变率均受频率变化影响较为明显,即频率越大,弹模衰减率、横向应变率和体积应变率越小,说明岩样刚度劣化速率随频率减小而增大,同时也表明加载频率对岩样的损伤发展过程有显著影响。
不同荷载条件下,岩石的损伤演化规律可通过不同损伤变量和模型进行描述。本文在结合前人研究基础上[16-17],根据先期研究提出方法[14],采用三种不同方法进行了损伤变量定义,即在塑性体积应变法、弹性模量法基础上,增加了峰值横向应变法进行描述,见式(1)~(3)。

(1)
DYM=(Es-Ei)/(Es-Ef)
(2)
DLAT=(ε3)i/εmax3
(3)
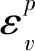
图5为根据上述方法所得岩样疲劳过程中的损伤演化规律。显而易见,三种不同变量所描述的损伤演化过程,呈“反倒S”型曲线,可分为三个阶段。初始损伤阶段,岩样损伤快速增加;但演化速率渐小至趋于恒定,也即损伤稳定发展阶段;后随加载次数的持续增加,损伤演化速率由恒定变为逐步加快,至快速增加,致使岩样发生最终破坏,此为损伤加速发展阶段。损伤演化规律与岩样塑性体积应变、横向应变和弹性模量随加载次数的变化规律一致,表明本文所采用表征损伤演化的变量与模型合理有效。
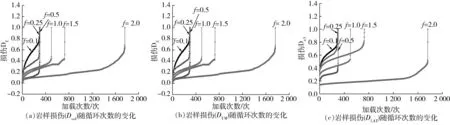
图5 不同频率条件下三个独立损伤变量随循环次数的演化规律Fig.5 Evolution of three independent damage variables with cycles under different frequency conditions
同样,对同一个岩样,其频率一样,但不同变量描述的损伤演化过程较为相似,表明在描述花岗岩疲劳损伤演化行为时,三个不同变量表征的方法一致性较好,其中塑性体积应变法与弹性模量法描述的过程更为接近[14-15]。
针对等速变形阶段的岩样损伤演化过程进行重点分析,如图6所示。从图6中可知,等速变形阶段的损伤演化速率均强烈依赖于频率的变化,表现出演化速率随频率f增大而非线性减小的特征关系。当频率大于0.5 Hz时,其损伤演化率随频率变化快速降低变为趋于平稳,表明此后频率的增加对岩样损伤的演化过程影响变小,同时图6中曲线也显示出三个不同变量获得的损伤演化速率特征规律基本相似,尤其对体积应变法和弹性模量法,为后续描述其他岩石的疲劳损伤演化规律提供了有效参考。
2.3 加载频率对岩石疲劳寿命的影响
图7为轴向加载频率对岩样疲劳破坏所需加载次数(疲劳寿命)的影响。由于岩样初始损伤一致的情况下,岩样的应变损伤变化滞后于应力变化,当频率f越高,应变损伤的积累还未完成,应力即已发生了卸荷,即单周循环引起的塑性应变随频率f的增大而减小,但由于岩样破坏时所承受的最大塑性应变基本相同,故其发生破坏所能承受的加载周次越多,即寿命越长。显然,频率越高,岩样的疲劳寿命越长,且呈现非线性快速增加,其关系可用指数函数来合理描述。

图6 频率对等速变形阶段损伤演化速率的影响Fig.6 Influence of frequency on damage evolution rate in constant velocity deformation stage
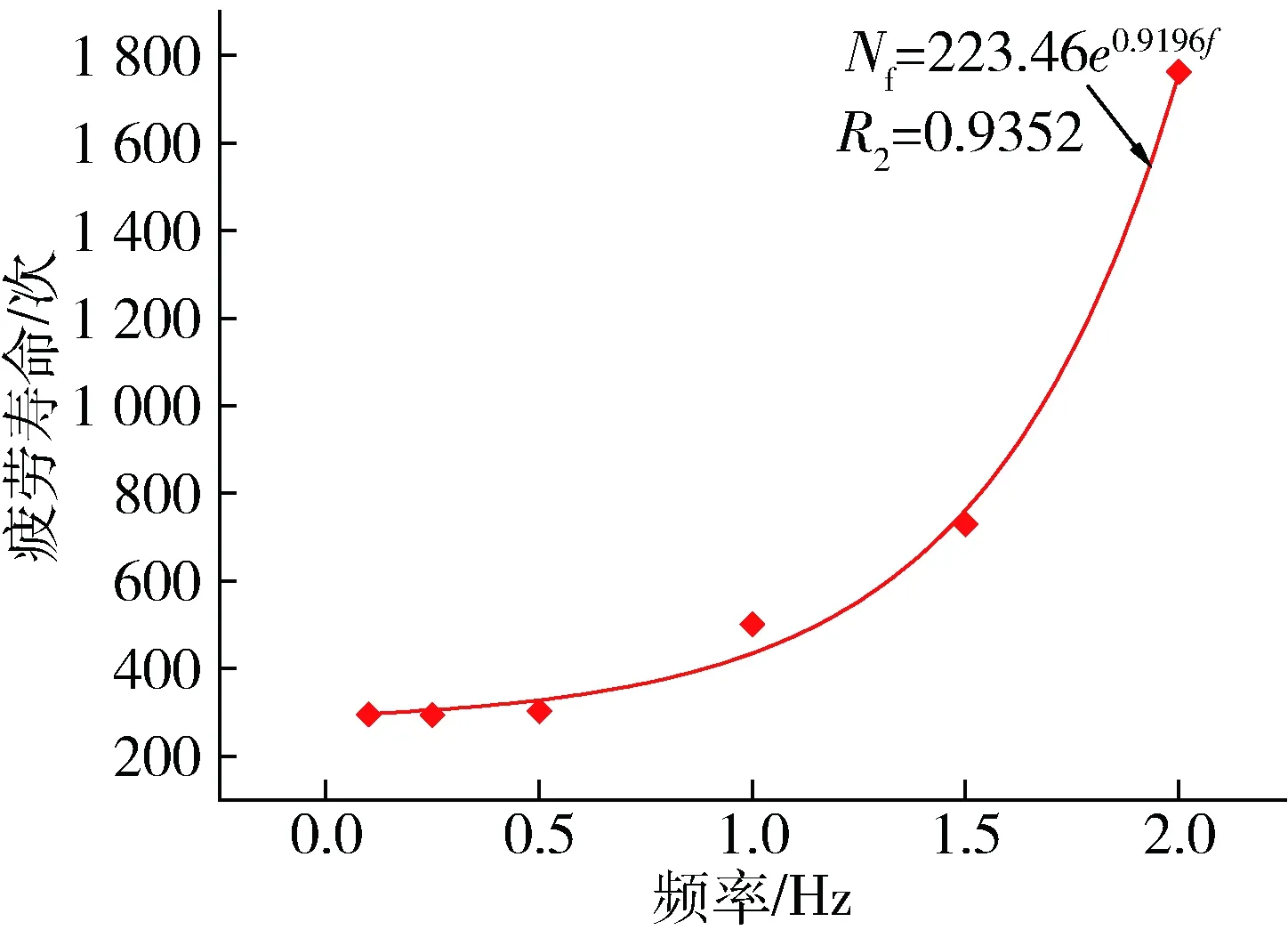
图7 加载频率对岩石疲劳寿命的影响Fig.7 Effect of loading frequency on fatigue life of rock
3 结 论
1) 北山花岗岩的强度和变形特性均一性较好,可作为研究花岗岩疲劳特性的有效试验对象。花岗岩的疲劳过程均可分为“疏-密-疏”三个特征阶段,这点不受试验条件的影响。
2) 频率的变化同样不会改变岩样最终破坏时所能承受的极限变形量,且对其最大塑性应变也无显著影响。
3) 采用塑性体积应变法、弹性模量法和横向应变法均可较为准确有效描述花岗岩的疲劳损伤演化过程,但塑性体积应变法和弹性模量法具有更为相似的行为特征,效果明显更优。
4) 岩样初始损伤一致的情况下,当加载频率f越高,岩样加载至破坏所需的次数越多,即疲劳寿命越长,并呈非线性增长趋势,可用指数函数进行合理描述。
