地锚式斜拉桥换索过程中无轴力铰受力分析

2019-04-16蒋伟冬张谢东郭子会

中外公路 2019年4期

蒋伟冬，张谢东，郭子会

(1.武汉理工大学交通学院，湖北武汉 430063； 2.内蒙古伊泰准东铁路有限责任公司)

1 引言

随着斜拉桥技术的飞速发展，斜拉桥存在的一些问题也慢慢显现出来。早年修建的斜拉桥由于设计与施工技术的不成熟，以及材料与工艺的不完善使斜拉桥存在自身缺陷，而在运营期间斜拉桥所受荷载的日益增加、后期维修养护不当等因素，使得斜拉桥各构件慢慢出现了使结构无法安全运营的一系列病害以及快速老化等现象，如桥面线形产生偏差，主梁和主塔出现裂缝，斜拉索及其锚具锈蚀等。目前为了解决由于斜拉索的腐蚀而使桥梁无法安全运营的问题，最常用的方法就是更换斜拉索。

跨中无轴力铰是针对地锚式斜拉桥这种特殊结构而创造发明的新技术。设计理论上要求无轴力铰仅能纵向滑移，同时传递桥梁剪力与弯矩。主塔、主梁的混凝土徐变收缩及自身的变位，活载的变化，斜拉索的松弛、索力下降，以及上述综合因素共同作用下所产生的桥梁跨中扭矩等，都会导致无轴力铰工作故障及病害。另外，无轴力铰的任何病害故障都会不同程度地影响到桥塔、主梁及斜拉索的受力状况，这种相互间的耦合作用使无轴力铰受力变得异常复杂。由于跨中无轴力铰的受力状态与索力密切相关，研究换索过程中该铰的受力状态十分必要，以确保跨中无轴力铰有效工作。

该文以湖北省十堰市郧县汉江大桥换索及维修工程为背景，该桥全长601 m，跨度布置为(86+414+86) m，边跨两岸的地锚式桥台长都是43 m，桥梁全宽15.6 m。采用有限元软件Abaqus建立无轴力铰实体模型，在Midas/Civil全桥模型的基础上，考虑换索时的实际工况，分析换索过程中无轴力铰受力性能以及安全性。

2 结构分析理论

无轴力铰长期处于高次超静定的空间体系中，其受力状态受到多种因素联合作用的影响。换索过程中不同编号索的卸除和张拉都会对无轴力铰的受力产生影响。

无轴力铰的主要结构为钢箱，其受剪力、弯曲和扭转的共同作用，与弯矩和扭矩相比剪力的作用相对较小，因此可以忽略剪力的影响，单根钢箱的受力情况简化如图1所示。

图1 箱形截面受弯扭作用

对于单根钢箱，考虑到钢箱的壁厚(t=24 mm)与宽度(d=1000 mm)的比值为0.024<0.1，若忽略加劲肋的作用而进行偏安全的强度验算，则可以把钢箱看成一闭口薄壁矩形截面杆。按照GB 50017-2014《钢结构设计规范》，对于单独受弯构件，其抗弯强度可按下式计算：

(1)

式中：Mx、My分别为对截面主轴x、y的弯矩；Wnx、Wny分别为对截面主轴x、y的净截面抵抗矩；γx、γy分别为截面塑性发展系数，对于箱形截面，γx=γy=1.05。

查阅现有文献[3]、[4]，依据下述假定：刚周边假定；理想弹塑性材料；材料屈服服从Mises准则；截面达到全塑性时，正应力与剪应力均为矩形分布。忽略大变形与应变硬化，并结合计算分析与试验研究，提出弯扭承载力设计需要满足相关性公式：

(2)

式中：Mp为截面全塑性弯矩；Tp为截面全塑性扭矩。

由以上公式可以得出单根钢箱的弯扭承载极限值，而实际结构中无轴力铰是由4根平行钢箱组成的，对于4根平行钢箱共同受弯扭联合作用，其受力状态要远比单根钢箱复杂，因此，需要建立无轴力铰的三维实体模型进行数值计算分析。

3 全桥模型建立

3.1 Midas模型的建立

全桥结构以有限元软件Midas/Civil为基础，以郧县汉江大桥施工图和竣工资料为依据建模分析。全桥采用空间杆系有限元模拟，模型共设1 106个节点，890个单元，主梁采用单主梁模型，主梁和斜拉索通过弹性连接里的刚性连接形成“鱼骨”式，斜拉索用桁架单元模拟，共200个单元。地锚索的地锚端将其各个方向的线位移和转角位移全部约束，主梁与地锚的过渡处以固结的形式进行约束。主梁与主塔混凝土标号为C50，取弹性模量E=3.5×107kPa，泊松比0.2，重度26 kN/m3。斜拉索采用直径为5 mm的低松弛预应力高强钢丝，其标准强度为1 570 MPa。索单元取重度78.5 kN/m3，泊松比0.3。具体模型如图2所示。

图2 郧县汉江公路大桥空间杆系模型

为了方便施工，该文按如下方式对拉索进行编号：参照图3，第一个字母区分主塔，十堰南塔记为S，郧县北塔记为Y；第二个字母区分中边跨，中跨索记为M，边跨索记为S；数字为序号，沿主塔向两侧由1递增至25；最后小写字母表示上下游，分别记为a、b。如郧县中跨上游第20号索记为YM20a。

3.2 换索前全桥模型的确定

运营多年后的斜拉桥，其主梁线形与内力已经和理想设计状态产生了偏差，要想准确地模拟换索过程，关键在于建立反映结构换索前实际内力和线形的计算模型。郧县汉江大桥经过施工过程的多次体系转换以及20多年的运营，全桥最终达到了换索前的状况，为了准确地模拟换索前的实际状态，建模时以该桥换索前实测索力和主梁线形为依据，通过调整索力、局部加载等技术方法，调整模型初始线形和索力至换索施工前的实际状态。

图3 全桥拉索布置

该文模型中斜拉桥索力与换索前实测索力误差全部在2%以内，且模型线形与实测线形也较为吻合。因此可以认为，该文模型已经接近换索前实际状态，满足换索过程的精度要求。以郧县侧为例，换索前模型索力和实测索力的对比如表1所示，其中实测索力取上下游实测索力的平均值。模型中跨标高与实际标高的对照如图4所示。

总体来看，Midas/Civil模拟结果与斜拉桥实际状况基本一致，存在的一些误差也都在允许范围内，说明Midas/Civil有限元模型准确地模拟了实际的结构状态，在此基础上采用整体-局部的有限元分析方法是可行的。

表1 换索前模型索力与实测索力对比

图4 换索前模型中跨标高与实际标高对照

4 无轴力铰模型建立

郧县汉江大桥无轴力铰是地锚式斜拉桥的重要构件，它关系到整个桥梁的受力状况及桥梁功能的正常发挥。从制作上来讲，该铰具有结构紧凑、受力明确等特点，同时也是根据地锚式斜拉桥受力特点而特别定制。为保证无轴力铰纵向可以滑移，同时能传递剪力与弯扭矩，郧县汉江大桥跨中两侧主梁上各设置两条支撑横梁，间距4 m，厚36 cm，近跨中的两端横梁中距1.3 m。接头段共25 m长，主梁为四室单箱截面，箱梁底板增至12.16 m，4根120 cm×100 cm，长10 m的钢箱，搁置在4根支撑横梁上，箱梁由厚24 mm的钢板焊接成封闭箱。钢箱与支撑横梁之间设25 mm×30 mm的四氟滑板支座，以便伸缩并传递剪力及弯扭矩。

4.1 模型材料参数

该文利用有限元软件Abaqus建立跨中无轴力铰实体模型，对其进行受力分析。该铰的受力由主梁通过四氟滑板支座传递到钢箱上，因此建立模型时截取部分主梁并建立实体模型。钢箱所用钢板采用旧国标16Mn钢，屈服应力345 MPa，各材料参数见表2。

Abaqus中量都没有单位，在使用其提供的单位制时必须保证它们内在关系统一，否则会导致计算结果与实际不符。该文选用国际标准单位进行计算，长度使用“m”为单位，力使用“N”为单位，质量使用“kg”为单位。为了准确有效地模拟实际结构，截取主梁跨中17.3 m进行计算，4根箱梁各长10 m，其纵断面如图5所示。

表2 材料参数

图5 跨中箱梁纵断面图(单位：mm)

建立一个合理可靠的有限元模型是保证计算准确性的基础工作之一，然而很多工程结构都比较复杂，若在模型建立时不对其进行简化会使分析变得非常困难，甚至出现计算无法收敛的情况，因此该文在建立钢箱的实体模型时，对其进行了适当的简化。钢箱由各种型号的钢板以及角钢焊接而成，在分析中忽略焊缝对结构强度的影响，且认为焊缝质量可靠，将整个钢箱作为一个整体。跨中无轴力铰采用有限元模型网格划分为1 393 444个净元。

4.2 边界条件及受力情况

边界条件是对结构位移的限制，需要根据实际工况条件来确定，现以Midas计算结果为基础，从中提取Abaqus计算所需要的边界条件以及结构所受外力。Abaqus实体模型梁端同时受到线位移和角位移的作用，由于无轴力铰能释放轴力且z方向的角位移可以忽略不计，因此线位移只考虑梁端竖向位移Dz，角位移考虑Rx和Ry的作用，其中y表示纵桥向，以郧县侧到十堰侧为正，x表示横桥向，以上游到下游为正。

为了分析跨中无轴力铰的结构安全性，考虑换索过程中钢箱最不利受力状况以及钢箱的受力变化，现选取3个工况对无轴力铰进行计算。工况1：换索前结构受力状况；工况2：卸掉YS25a，YM25a索时受力状况；工况3：卸掉YS25a和YM25a索且考虑索相对混凝土温度高15 ℃时受力状况。由Midas提取的边界位移如表3所示。

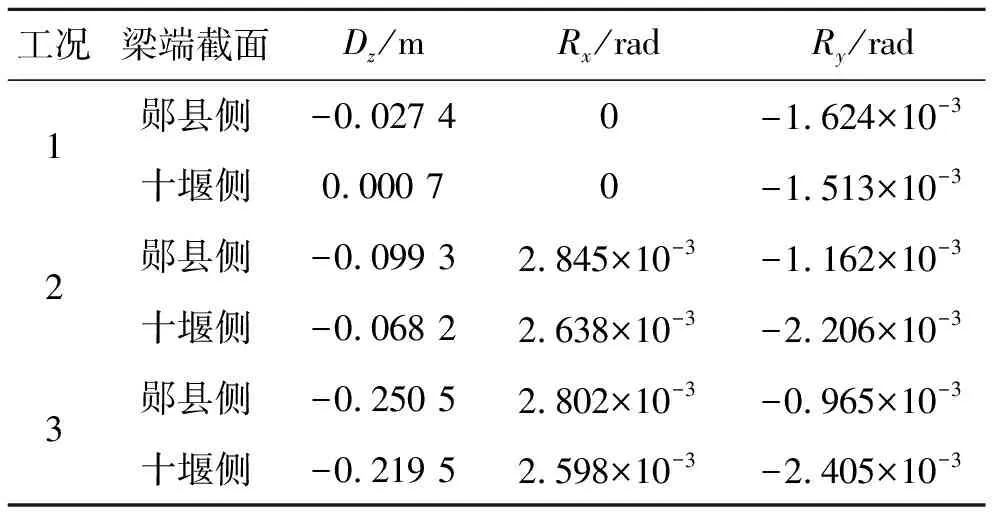
表3 梁端各工况时的位移

由表3可知：除了梁端存在位移外，该节段梁还承受跨中最长索(YM25a，YM25b，SM25a，SM25b)索力的影响，索力可分解为竖向力和水平力，由于无轴力铰不传递轴力，只需考虑竖向力的影响，其索力F及竖向分力Fz如表4所示。

为了方便计算结果的对比分析，将无轴力铰的4个钢箱进行编号，从上游到下游(沿Y轴正方向)分别称为钢箱1、钢箱2、钢箱3和钢箱4。

表4 跨中最长索各工况索力 kN

4.3 模型计算

4.3.1 无轴力铰受力分析(工况1)

理论上由于地锚式斜拉桥的对称性，合理成桥状态下跨中无轴力铰应处于应力最小或接近无应力状态，但换索前的斜拉桥已运营多年，线形和索力的变化必然使跨中钢箱承受力的作用，为了了解无轴力铰的工作现状，研究换索前钢箱的受力状况是很有必要的。工况1为换索前结构的受力状况，有限元分析结果如图6所示。

模型中同号斜拉索上下游索力相等，同时整体承受Dz和Ry位移的作用，由于结构、位移以及索力都是上下游对称分布，因此4根钢箱的应力分布也应上下游对称。从图6可以看出钢箱1和4以及钢箱2和3的应力状态相同，且钢箱1和4的应力要大于钢箱2和3的应力，最大应力为27.59 MPa，由图6可知最大应力出现在钢箱1和4的跨中横隔钢板上，但远小于钢箱的屈服强度。

图6 各钢箱应力分布图(单位：Pa)

4.3.2 无轴力铰受力分析(工况2)

工况2为卸掉YS25a和YM25a索后无轴力铰的受力状况，该工况是实际施工过程中对跨中产生最不利影响的工况，为了确保换索过程中结构安全，有必要对跨中无轴力铰进行受力分析，其有限元分析结果如图7所示。

从图7可以看出：每根钢箱的应力分布基本一致，卸掉YS25a和YM25a索后钢箱应力最大值为55.8 MPa，由于此工况卸掉的是上游斜拉索，因此最大应力出现在最上游的钢箱(钢箱1)上，往下游方向各钢箱的最大应力逐渐减小，由钢箱1～钢箱4最大应力逐渐递减，分别为55.80、46.34、41.51和39.85 MPa，最大应力都出现在钢箱的中部。

4.3.3 无轴力铰受力分析(工况3)

工况3为在工况2的基础上考虑索相对混凝土温度高15 ℃时无轴力铰的受力状况，在卸长索时是处于夏季，当地白天气温高，且旧索拆除到新索安装往往要1～2 d的时间，白天日照作用下，索的温度会比混凝土高出10～20 ℃，因此研究该工况下无轴力铰的受力也是很有意义的，其有限元分析结果如图8所示。

图8 各钢箱应力分布图(单位：Pa)

从图8可知：其变化趋势与工况2一致，但应力整体都有所增加，最大应力达到67.67 MPa，比工况2增大了11.87 MPa，但仍然远小于钢箱的屈服强度。4根钢箱的最大应力依然是从钢箱1至钢箱4逐渐减小，最大应力同样都靠近钢箱的中部，分别为67.67、58.22、53.40和51.78 MPa，比工况2都大了接近12 MPa，说明温度对结构的受力影响比较大。

4.3.4 各工况结果对比

由上述3个工况结果分析可知：在各工况下每根钢箱的最大应力都出现在接近中间的部位，换索前由于结构已经偏离原设计状态，4根钢箱都产生了一定程度的应力，但都远远小于钢箱的屈服强度，仍然能满足安全使用要求。卸掉最长索后无轴力铰钢箱的受力发生了较大变化，具体变化情况如图9所示。

图9 各工况各根箱梁最大应力对比图

工况2卸掉YS25a和YM25a索后各根钢箱的最大应力比工况1卸索前都有明显增加，增量最大的是钢箱2，应力增大了39.7 MPa，但应力最大值依然出现在钢箱1上，其最大应力也增加了1倍左右。工况3与工况2相比，每根钢箱的最大应力增量基本一样，都接近11.9 MPa，说明温度对跨中无轴力铰的受力影响很大，在实际工程中不可忽视。从同一工况的不同钢箱最大应力结果可以看出，卸掉上游索对靠近上游的钢箱产生的影响最大，而且从上游至下游影响依次减小，由结构的对称性可知，卸掉下游索也会出现同样的情况。

对跨中无轴力铰产生最不利影响的工况3使钢箱产生的最大应力为67.67 MPa，远远小于钢箱的屈服应力345 MPa，因此可以确定在整个换索过程中跨中无轴力铰钢箱始终处于安全状态，而且安全系数较高。