探究数学史中的勾股定理的证明

◆吴心培

(江苏省华罗庚中学)

一、引言

勾股定理也称毕达哥拉斯(Pythagoras)定理，是数学中非常重要的定理之一。毕达哥拉斯是公元前6世纪希腊著名的数学家和哲学家，在西方，他被普遍认为是该定理最早的证明者，因此勾股定理就以他的名字命名。然而早在公元前1700年，古巴比伦人就发现已这一定理，无独有偶，最迟公元前1105年，我国的商高便能利用一般的“弦图”来证明这一定理。时至今日，勾股定理的证明方法已经有400多种了，其推论及应用仍具有重要影响。本文将对几种著名的勾股定理的证明方法进行简要介绍。

二、中国古代勾股定理的证明

1.《周髀算经》中商高的证明

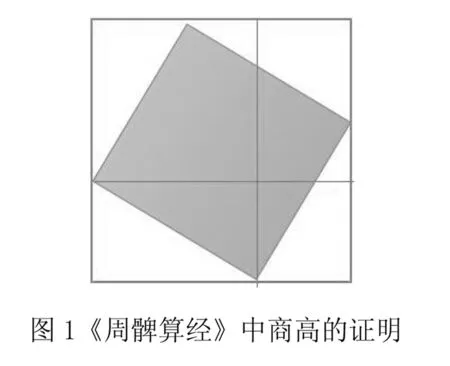
《周髀算经》是我国古代最早的数学著作，其内容包括天文、数学知识，表现了我国古代人民的伟大智慧。《周髀算经》中记载了周公与大夫商高的一段话，商高当时回答说：“故折矩以为勾广三，股修四，径隅。既方其外，半之一矩，环而共盘。得成三、四、五，两矩共长二十有五，是谓积矩。故禹之所以治天下者，此数之所由生也”。

英国人Joseph Needham将这段文字解释为：把一个矩形沿对角线剪开(如下图1所示)，宽等于3个单位，长为4个单位。这样两对角之间的对角线长为5个单位。我们再用这条对角线为边画一个大正方形，再用几个同上文的半矩形把这个大正方形围起来，从而形成一个方形盘。像这样，外面四个半矩形便构成了两个矩形，这两个矩形总面积是24，然后我们再从方形盘的总面积49中减去24，得到25。我们便称这种方法为“积矩”。

虽然书中只以3，4，5为例，但这种方法也具有一般性，所以我们普遍认为商高已经证明了勾股定理。

2.《九章算术》中刘徽的证明

《九章算术》是《周髀算经》之后最重要的数学典籍，这部学术著作是由先秦到西汉中期众多的学者修改编纂而成的，其在代数、几何方面均有巨大成就。可以说，它代表着中国古代的机械算法体系，它与古希腊的《几何原理》相得益彰，对东方的数学发展产生重要影响。

魏晋时期，著名数学家刘徽在为《九章算术》做批注时便给出了自己的证明：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也。合成弦方之幂”，短短几句便对勾股定理进行了清晰的描述。但十分可惜的是，刘徽的证明的图已经失传了。根据学者李迪的研究，刘徽的证明方法与欧几里得在《几何原本》中的证明描述相似，而根据学者曲安京先生的研究，刘徽的勾股定理证明方法如图2所示，其他学者对刘徽的证明方法也有自己不同的理解和阐述。

3.《勾股举隅》中梅文鼎的证明

梅文鼎是我国清代著名的学者，是民间数学家和天文学家，被誉为“国朝算学第一人”。对于勾股定理的证明，梅文鼎给出了两种证明方法，其中一种方法与赵爽和刘徽的方法有异曲同工之妙。本文介绍梅文鼎另外一种独具创造性的证明方法，具体步骤如下：

(1)以直角三角形ABC斜边BC为边作一个正方形BCDE，其面积为BC的平方，再过点A做BC的垂线KL，把正方形分割成面积为AC平方的四边形DKLC与面积为AB平方的四边形KEBL，如图3所示。

(2)将三角形ALC，ALB移到FKD，FKE处，并做AI垂直于FD，做EN垂直于FE，如图4所示。

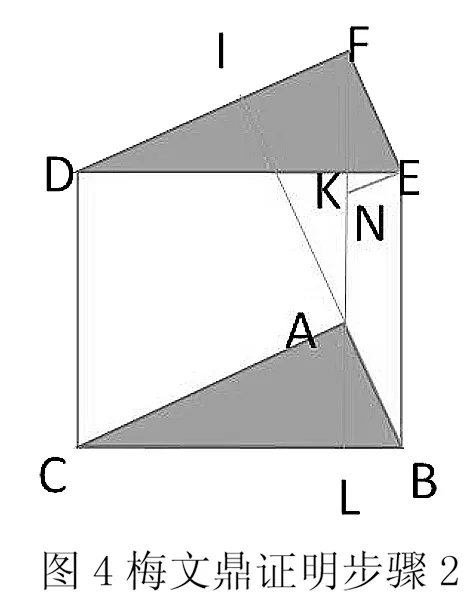
(3)将三角形FLA，FEN移到DHC，EJM处，如图5所示。

(4)将梯形ENAJ移到JMBG处，即可完成证明，如图6所示。

三、国外勾股定理的证明

1.Plato的证明

毕达哥拉斯提出勾股定理之后，希腊哲学家Plato给出了关于该定理一种特殊情况的证明。他运用的方法为“割补法”，通过几何的变换来进行证明，具体证明步骤如下：

Plato对等腰直角三角形的情况做出了证明，将其腰上的两个正方形沿对角线分割成为两个全等的等腰直角三角形，再将这四个三角形拼到斜边上，成为一个新大正方形。由于是平移操作，所以各部分面积不变，从而又可以用“面积法”得证。虽然说这是一种特殊情况，但是这也为后世提供了“割补”的数学思想，如图7所示。

2.Euclid的证明

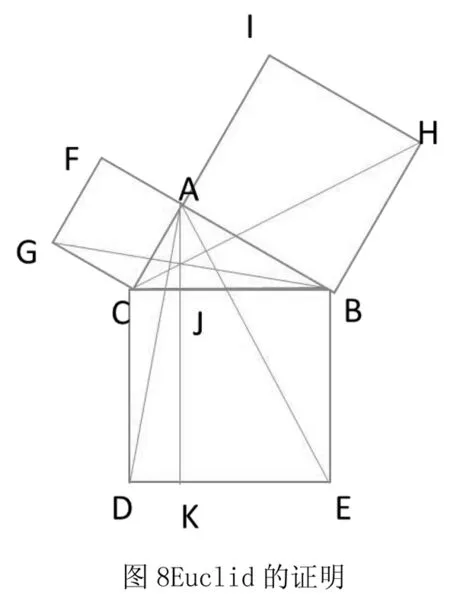
Euclid的证明是欧洲有记载的最早的勾股定理的证明。在Euclid所著《几何原本》卷一的命题47中，Euclid给出了自己的证明。在证明的过程中，Euclid运用到了图形割补、等边三角形和面积的关系，其具体证明过程如下：

如图8所示，在直角三角形ABC的各边上做正方形，可以看到三角形ACD与GCB全等，三角形ADC的面积就等于四边形CDKJ的一半，三角形GCB的面积是四边形AFGC的一半，所以四边形CDKJ的面积等于四边形AFGC的面积。同理，四边形JKEB的面积等于四边形ABHI的面积。于是得到AB2+AC2=BC2，定理得证。

在思想方面，Euclid也继承了Plato的割补思想，只是具体过程略有不同而已，他们两人的思想方法都为后世对于勾股定理的证明提供了思路。

3.Leonardo Da Vinci的证明

达芬奇是众所周知的文艺复兴时期的数学家、解剖学家与画家。他在《几何原本》证明图的基础上，上下各添加了一个直角三角形，拼接而成两个面积相等的连六边形BCGFIH和JEBACD，再运用面积相减法，于是就可以证明勾股定理了。这也是运用的一种割补的思想，但他却和Euclid的方法有着细微的差别，从几何变化的角度上来看的话，达芬奇主要运用的是旋转和对称，而后者运用的则是平移，如图9所示。

四、勾股定理的推广

1.勾股定理在三维空间里的推广

由于勾股定理条件中有一组垂直的关系，结论中有一组“平方和”关系，我们由此联想，在空间结构中可以构建一个三棱锥，使得组成这个三棱锥的三个侧面的三条线段两两垂直，从而使得二维的线段的平方关系成为三维的面的平方关系，如图10所示。根据我们的猜想，三角形ABC面积的平方应该等于三角形OAB，OAC，OBC各自面积的平方之和。证明过程如下：

我们作OH垂直于平面ABC，垂足为H，连接CH并延长交AB于E，连接OE，我们可以得到H为△ABC的垂心，且AB垂直于OH。

由射影定理可以得到OE2=EH×CE。

∴S2△ABO=1/4×AB2×EH×CE=1/2×AB×EC×1/2AB×EH=S△ABC×S△ABH

同理，S2△OBC=S△ABC×S△CBH，S2△OAC=S△OAC×S△CAH.

联系上式即可得证猜想成立，于是，我们就得到了空间勾股定理。

2.勾股定理在面三角形中的运用

我们用类似直角三角形的做法，构造出有两个直角三角形面的“面直角三角形”，如图11所示。沿袭上文思路，我们猜想：四边形ADEF的面积的平方等于四边形ADCB的面积的平方加上四边形CBFE的面积的平方。

我们用S代表四边形AFED的面积，S1代表四边形ABCD的面积，S2为四边形BFEC的面积。具体证明过程如下：

∵S=AD×AF，S1=AB×AD，S2=EF×BF.

∴S2=AD2×AF2，S12=EF2×AD2，S22=EF2×BF2.

又∵AD=EF=CB，CE=BF，

∴S2=BC2×(AB2+BF2)，S12+S22=AB2×AD2+EF2×BF2.

于是：S2=S12+s22.

五、小结

勾股定理是人类文明史上的一颗耀眼的明星，是“几何学的基石”，它的诞生产生了许多与它相关的数学思想，进而使得世界上几个文明古国都对它进行了深入的研究。时至今日，勾股定理的证明方法已多达400多种，本文对勾股定理证明中用到的面积法，拼接法等都给出了一些经典的例子。随着科技的进步和社会的发展，勾股定理将会推广到更深更远的地方。例如，在三维空间中，在面三角形上，或是在n维空间中。勾股定理作用广泛，博大精深，更深层次地研究还需进一步探索。