荷载横向作用位置对偏心荷载分解法影响分析
2019-04-15李夏元万水Mo
李夏元, 万水, Y.L. Mo
(1.东南大学 交通学院, 江苏 南京 210096; 2.Civil and Environmental Engineering, University of Houston)
1 前言
薄壁箱梁截面因其抗弯、抗扭性能好,广泛应用于桥梁结构。近年来,随着预应力技术在桥梁领域的发展与应用,箱梁截面大量采用腹板间距较大的宽箱形式。结构承受车轮荷载作用时,荷载多偏离箱形梁扭转中心,箱形梁将发生截面扭转,而宽箱截面因其箱室较宽,偏心距大,扭转效应更为明显。文献[2]表明箱形梁在扭转过程中,由刚性扭转和截面畸变产生的纵向翘曲应力可达到纵向总应力的24%~26%。薄壁箱梁因偏心布置的汽车荷载而产生的附加翘曲应力在活载总应力中占有较大的比例,已成为大跨箱梁桥设计计算中必须考虑的问题。
近年来,关于横向偏心荷载作用下箱形梁的力学性能研究主要分为有限单元法和理论解析法。有限单元法随着计算机的发展而迅速发展,在土木工程中应用越来越广泛,但不易对箱形梁的工作性能获得明确的物理概念, 对于参数分析与方案选择无法给出直观说明;理论解析法的主要思路是:箱形梁在偏心荷载作用下,根据线弹性叠加原理,将荷载分解为正对称荷载与反对称荷载分别进行计算,然后两者叠加,偏心荷载分解法概念明确,适用于横截面任意荷载作用的情况。尽管偏心荷载分解法存在诸多优势,但当前文献在介绍偏心荷载分解时,均基于力的平移定理,偏心荷载分解与截面参数无关,只与偏心距有关,忽略了腹板刚度对顶板的约束情况,这与实际情况存在一定的偏差。荷载横向作用位置变化对偏心荷载分解法的影响因素研究尚未见报导。目前,国内外学者针对箱形梁空间效应理论(剪力滞、扭转和畸变)进行了大量的试验和理论研究,并取得了一定的成果,而相关研究的发展都是基于特殊的力学加载模式下开展的——外荷载以各种形式作用于箱梁腹板上,具有工程应用的局限性,荷载横向作用位置对偏心荷载分解法影响的研究恰恰能够解决这样的局限性,拓宽理论的适用范围,对工程实际具有重要的指导意义和现实意义。
该文以单箱单室薄壁混凝土箱形梁为研究对象,理论论证当前偏心荷载分解法的局限性。依托Abaqus有限元数值分析软件,选取箱形梁顶板厚度、腹板厚度、梁宽、梁高等因素进行参数化建模,基于控制变量原则,分析横向荷载作用位置对偏心荷载分解法的影响,提出任意横向位置下偏心荷载分解的简化计算方法。
2 横向偏心荷载分解法理论分析
文献[11]给出如图1所示的偏心荷载分解模式,分解思路:作用于箱梁顶板的偏心荷载P,根据力的平移定理,将偏心荷载P平移到箱形梁的扭转中心,外加一个扭矩P·e。作用于扭转中心的集中力P和扭矩P·e可以分解成正对称荷载和反对称荷载,相邻腹板的合力可以等效成外荷载F1、F2。
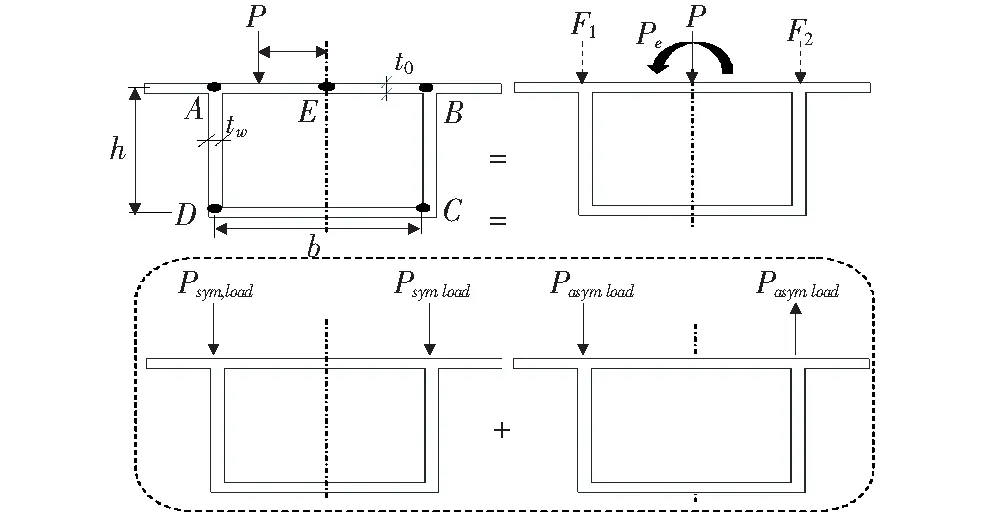
图1 偏心荷载分解示意图
由图1可列出横向偏心荷载分解下F1、F2、Psym,load(对称荷载)、Pasym,load(反对称荷载)这4个未知分量的力的平衡方程:
(1)
由式(1)可得:
由于未知数数量超过平衡方程数目,文献[11]增设一个力矩平衡方程:
Pasym,load·b=P·αb
Pasym,load=αP
(2)
现论证式(2)的合理性。F1、F2可表示为:
(3)
(4)
其中:0≤α≤0.5。
比较F1、F2的值,可以发现,偏心荷载分解法的结果与两端简支约束下的内力分配一致,如图2所示。

图2 等效简支梁示意图
上述结论表明:传统偏心荷载分解法忽略了腹板刚度对顶板的约束情况,仅仅以简支约束代替,实际上腹板刚度对顶板存在着约束作用。因此,仅仅用简支约束来代替边界条件是不合理的,即式(2)的假设有待商榷。
由式(1)结论可知:偏心荷载分解得到的正对称荷载Psym,load值恒定为P/2,与外荷载横向作用位置以及截面参数无关,而反对称的荷载值Pasym,load与偏心荷载各腹板力F1、F2的分配有关,当偏心荷载作用于A时(即α=0.5),反对称荷载值Pasym,load恒定为P/2,与截面参数无关。
3 研究方案确定
由式(1)可知:横向荷载作用位置的变化对正对称荷载的取值没有影响(Psym,load=P/2),仅影响反对称荷载的取值,这是由边界条件决定的。横向荷载作用位置对偏心荷载分解法的影响主要表现在相邻腹板荷载的分配,最终反应到反对称荷载Pasym,load的力的分配。因此,为研究横向荷载作用位置对偏心荷载分解法的影响,可通过研究横向荷载作用位置对反对称荷载Pasym,load力的分配影响来实现。正对称荷载下结构的反应可用弯曲应力σsym,w表示,而反对称荷载下结构的反应可用扭转畸变翘曲应力σasym,w表示,偏心荷载下的纵向总应力可用σPw来表示。三者之间必然满足:
σPw=σsym,w+σasym,w
(5)
根据图1 所示的偏心荷载分解图,利用Abaqus有限元软件分别建立偏心荷载P(α=0.25、0.375、0.5)、正对称荷载Psym,load=P/2、反对称荷载Pasym,load=P/4共3种加载工况下的有限元模型。式(1)中,Pasym,load荷载值是未知的,选取Pasym,load=P/4,可以利用式(6)得到横向任意荷载作用下,反对称荷载Pasym,load与偏心荷载P之间的数值关系k,绘制k的横向影响线,提出反对称荷载系数k的简化计算方法。
(6)
3.1 截面参数
选取跨度为2.5 m的单箱单室薄壁箱梁为基准模型,模型截面尺寸见图3,材料的弹性模量E=3.45×104MPa,泊松比υ=0.2。力学加载模式为跨中截面分别作用图1所示的偏心荷载P=25 kN、正对称荷载P/2=12.5 kN以及反对称荷载Pasym,load=25/4 kN。

图3 薄壁箱梁横截面图(单位:mm)
以箱形梁顶板厚度t0、梁宽b、梁高H等参数作为变量,基于控制变量原则,利用Abaqus有限元软件对上述力学加载模式分别进行三维数值建模分析(图4~6)。

图4 偏心荷载加载模式

图5 对称荷载加载模式
3.2 测点选取
文献[14]表明:正对称荷载作用下,加载点截面底板出现正剪力滞,箱形梁弯曲正应力最大值出现在底板角点D处;文献[11]、[13]表明:反对称荷载作用下扭转和畸变翘曲正应力最大值出现在箱形梁底板角点D处。因此,选取D点作为研究对象,绘制箱形梁角点D处纵向应力沿梁轴的变化规律。
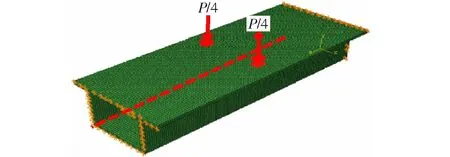
图6 反对称荷载加载模式
4 参数分析
4.1 算例分析
以图3为例,偏心加载点位置e=0.25b。分别提取偏心荷载作用下测点D沿梁轴方向的纵向应力值σPw(Peccentric,load)、对称荷载作用下测点D沿梁轴方向的弯曲应力值σsym,w(Psym,load)、反对称荷载Pasym,load=P/4作用下测点D梁轴方向的扭转和畸变翘曲应力值σasym,w(Pasym,load)以及正对称荷载弯曲应力值σsym,w与反对称荷载作用下的扭转畸变翘曲应力值σasym,w和值,分别绘制于图7。

图7 沿梁轴方向的纵向应力
由图7可见:偏心荷载P作用下测点D的纵向应力值大于正对称荷载和反对称荷载作用下的应力和值,表明当偏心距e=0.25b时,反对称荷载Pasym,load=P/4计算扭转畸变翘曲正应力值是偏小的,即实际结构在靠近加载点腹板分配的力较多,与式(2)的设定存在偏差。按式(6)计算偏心荷载P作用于e=0.25b位置时其反对称荷载系数k,k=0.341,即k≠α=0.25。
图8为偏心荷载P作用下的纵向应力值σPw与正对称荷载和反对称荷载作用下的应力和值σsym,w+σasym,w沿梁轴线方向的误差δ(%)。
(7)
由图8可知:沿梁轴线方向的误差δ不是固定值,在两端误差最小为10.3%;3L/8与5L/8处误差达到最大值12.63%;加载点截面处的相对误差为10.64%,该点处绝对差值最大,且与最大误差仅差2%。因此,选取加载点截面测点D纵向应力值,按式(6)计算反对称荷载系数k是可行的。
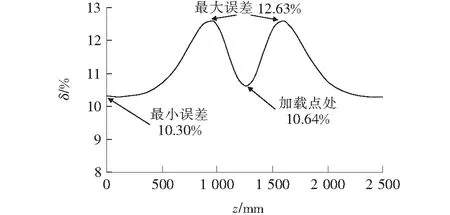
图8 δ 误差分析图
4.2 宽跨比b/L
宽跨比b/L为箱梁腹板之间的间距b与跨径L的比值,相邻腹板之间的间距分别选取b=300、600、800、1 000 mm,控制截面参数如图3所示。利用Abaqus有限元软件分别建立不同宽跨比下的数值模型,提取不同荷载工况下测点D的纵向应力值,利用式(6),绘制如图9所示的反对称荷载系数k随宽跨比b/L的变化规律。
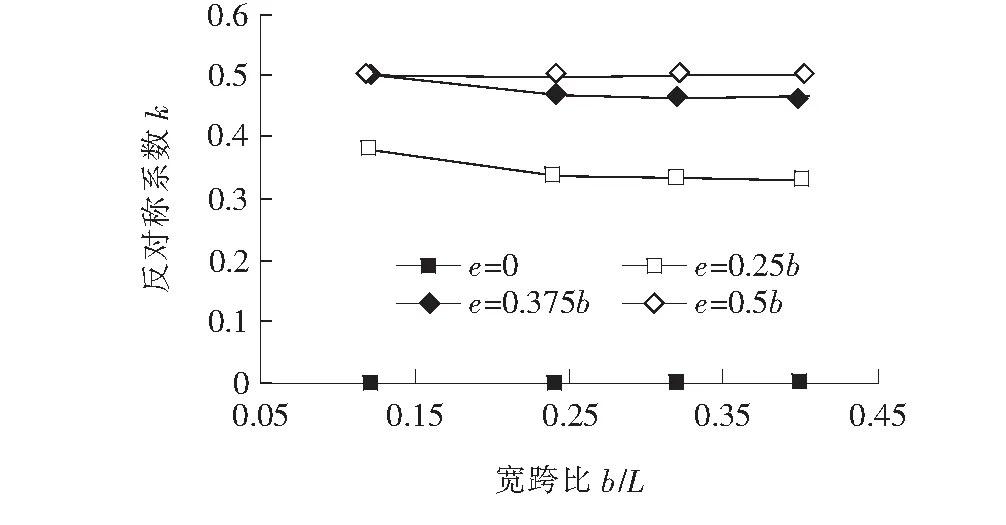
图9 反对称荷载系数k随宽跨比b/L的变化规律
由图9可见:反对称荷载系数k随着宽跨比b/L的增大而逐渐降低,但变化幅度相对较缓,当b/L从0.12变化到0.24时,反对称荷载系数k的变化相对较大,而当b/L>0.24时,宽跨比b/L对反对称荷载系数k的影响几乎可以忽略。
4.3 高跨比H/L
高跨比为箱形梁高度H与跨径L的比值,控制截面参数如图3所示,仅改变梁高,分别取梁高H=240、440、640、840、1 040 mm,利用Abaqus有限元软件分别建立不同高跨比下的数值模型,提取不同荷载工况下测点D的纵向应力值,利用式(6),绘制如图10所示的反对称荷载系数k随H/L的变化规律。
由图10可见:偏心距e=0.25b时,反对称荷载系数k随着高跨比H/L的增大,先缓慢增大后缓慢减小,变化幅度不大;偏心距e=0.375b时,反对称荷载系数k随着高跨比H/L的增大而减小,反对称荷载系数k的数值曲线呈现相对平缓的趋势。表明高跨比H/L对反对称荷载系数的影响相对较低,可以忽略不计。

图10 反对称荷载系数k随高跨比H/L的变化规律
4.4 高宽比H/b
取3.2节与3.3节不同宽度和高度的反对称荷载系数,绘制如图11所示的反对称荷载系数k随高宽比H/b的变化规律,进一步验证箱形梁高度和宽度对反对称荷载系数k的影响。
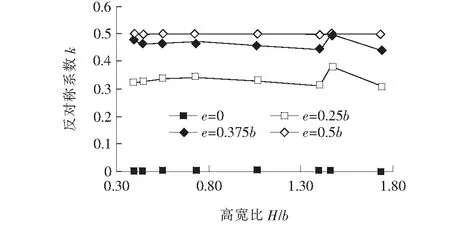
图11 反对称荷载系数k随高宽比H/b的变化规律
由图11可见:反对称荷载系数k随着高宽比的增加,变化相对比较平缓,当箱形梁宽度为300 mm时,高宽比H/b为1.47时,有较为明显的波动,与图9相似,这是因为箱形梁截面宽度较窄,局部影响显著增强。总体而言,高宽比对反对称荷载系数k的影响可以忽略不计。
4.5 顶板厚度与腹板厚度比t0/tw
控制各项参数如图3所示,改变顶板厚度t0,顶板厚度t0分别取20、30、40、50、60、70、80 mm,t0/tw变化范围0.5~2.25,步长为0.25。利用Abaqus有限元软件分别建立不同顶板厚度下的数值模型,提取不同荷载工况下测点D的纵向应力值,利用式(6),绘制如图12所示的反对称荷载系数k随t0/tw的变化规律。

图12 反对称荷载系数k随顶板与腹板厚度比
由图12可见:偏心距e=0.25b和e=0.375b下的反对称荷载系数k随着顶板厚度与腹板厚度比值t0/tw的增大而逐渐减小。t0/tw<1.5时,反对称荷载系数k的值变化较为迅速,t0/tw≥1.5时,反对称荷载系数k变化相对平缓,呈线性变化规律。当t0/tw<1、e=0.375b时,反对称荷载系数k的值超过了0.5,这一现象意味着当顶板厚度比腹板厚度薄时,反对称荷载引起的扭转畸变翘曲应力显著增大,若按式(2)的结论,反对称荷载系数仅为0.375,误差超过30%;而当t0/tw<1、e=0.25b时,误差更是超过56%,这一现象必须予以重视。
5 反对称荷载系数k的简化计算方法
由上述参数分析可知,顶板厚度与腹板厚度比值t0/tw对反对称荷载系数k起主要作用,而高度、宽度等因素对反对称荷载系数k影响则可忽略不计。该节将重点分析反对称荷载系数k的简化计算方法。
当t0/tw=2.25时,绘制反对称荷载系数k随偏心距系数α改变时的变化趋势于图13,并添加函数趋势线。
由图13可知:反对称荷载系数k与偏心距系数α成线性变化的规律,且趋势线拟合程度指标R2≈1,反对称荷载系数k与偏心距系数α拟合程度具有较强的可靠性;相关系数ρkα:
(8)
反对称系数k与偏心距系数α线性相关性较强,可按k=α表示。
由式(2)可知:
(9)
反对称荷载系数k等于偏心距系数α,表明当t0/tw≥2.25时,顶板刚度较大,腹板对顶板的约束可以看成铰接约束,反对称荷载系数k按照式(2)进行计算,反对称荷载Pasym,load=k·P,k=α。
当t0/tw=1时,绘制反对称荷载系数k随偏心距系数α改变时的变化趋势于图14,并添加函数趋势线。
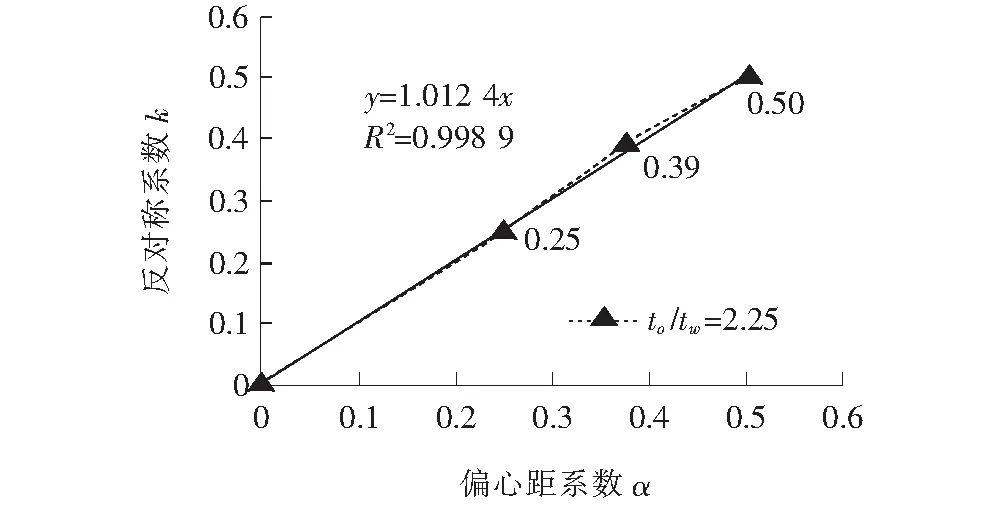
图13 反对称荷载系数k随偏心距系数α的
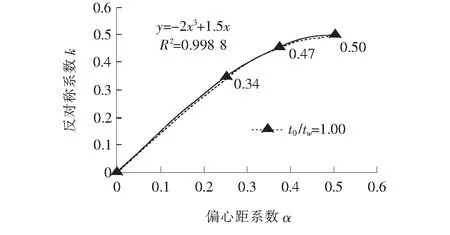
图14 反对称荷载系数k随偏心距系数α的
由图14可知:反对称荷载系数k与偏心距系数α成3次抛物线变化的规律,趋势线拟合程度指标R2≈1,反对称荷载系数k与偏心距系数α拟合程度具有较强的可靠性:
k=-2α3+1.5α
(10)
类比文献[15]给出两端固定约束下的内力分配计算方法。
(11)
将式(11)代入式(1),可得:
(12)
式(12)与式(10)结论一致:
(1) 当t0/tw=1时,箱形梁腹板对顶板的约束相当于固定端约束。
(2) 当1≤t0/tw<2.25时,反对称荷载系数k与偏心距系数α的函数关系介于简直约束与固定端约束之间,可按固定端约束情况进行分析,通过式(10)得到的反对称荷载系数k可以包络之间的所有数值(图12),反对称荷载Pasym,load=k·P,k=-2α3+1.5α。
(3) 当t0/tw<1、偏心距e=0.375b时,反对称荷载系数k>0.5,顶板厚度to越薄,其局部效应越明显,不能简单用上述等效成腹板对顶板的约束情况进行分析。建议在按固定端约束等效计算的同时,考虑对反对称荷载系数k进行修正:
(13)
6 结论
该文从理论出发,论证了传统横向偏心荷载分解法的局限性,探讨了反对称系数k随箱形梁顶板厚度与腹板厚度比t0/tw、宽跨比b/L、高跨比H/L、高宽比H/b等参数变化的规律,基于控制变量原则,利用Abaqus有限元软件,就如图1所示的加载模式分别进行三维数值建模分析,得到如下结论:
(1) 横向偏心荷载分解法对正对称荷载力的分配无影响,Psym,load=P/2,主要影响反对称荷载Pasym,load力的分配。文献[2]、[4]、[7]关于箱形梁的扭转和畸变效应理论分析仅适用于偏心荷载e=0.5b的情况,具有工程应用局限性。
(2) 箱形梁宽跨比b/L、高跨比H/L、高宽比H/b等参数变化对反对称荷载系数k的影响较小,可以忽略不计;而箱形梁顶板厚度与腹板厚度比t0/tw对反对称荷载系数k影响较为明显,反对称荷载系数k随着箱形梁顶板厚度与腹板厚度比t0/tw的增大而减小。

(4) 该文提出的反对称荷载分配计算方法弥补了文献[2]、[4]、[7]应用的局限性,适用于横向任意位置作用偏心荷载的情况。
