帽儿山8种常见绿化木本植物的叶片“收益递减”假说检验
2019-04-14丛健
丛健
(辽宁省林业发展服务中心,辽宁 沈阳 110036)
全球植物叶片大小变化高达6个数量级[1]。叶片大小是植物适应环境对策的重要指示者[2-4]。叶大小的变化主要通过影响叶边缘对热量、二氧化碳和水分的传导能力来影响整个植株的生长速率[5]。叶片大小理论在40年前就已经建立起来[6]。大叶也会增加树木的自我荫蔽(Self-shading),从而影响光截获和潜在碳吸收的种间变异[2]。自我荫蔽叶片大小与很多功能性状之间都存在着协变关系,共同决定着植物对环境的响应及其适合度变化[5]。因此,植物叶片大小是植物对策的一个重要方面[4]。
植物叶片的异速生长关系研究有助于理解植物叶片大小的投资—收益。叶片质量代表投资,而叶片面积是光能截获的表现,代表收益。叶面积与叶质量的关系常用指数定律函数描述:A=βMα(A为叶面积,M为叶质量,α为异速生长幂次,β为标准化常数)。在实际计算中,经常幂函数作对数转化(lgA=lgβ+αlgM),用斜率α表达异速生长[1]:α< 1表明叶面积增加慢于叶质量增加,为“收益递减(diminishing returns)”;α> 1正好相反,为“收益递增(increasing returns)”;α= 1为等速生长,可称为“收益稳定(constant returns)”。全球尺度研究表明,种间叶面积与叶质量大多呈异速生长关系,叶面积增长比叶质量慢(α<1),即存在“收益递减”规律,而树木呈“收益递增”规律。但是这些全球尺度的数据分析,不可避免地受到环境和系统发育引起的变异的影响而产生不确定性。针对157个物种内叶面积与叶质量异速生长关系的研究表明,跨物种尺度叶片大小随叶质量增加呈“收益递增”型;但其中61个为“收益递减”型,仅7个为“收益递增”型[7]。在辽宁西部地区55个园林绿化树种中,即便气候和资源高度相同,不同植物间叶片大小依然变异很大,跨物种尺度为“收益稳定”型,但其中46个树种为“收益递减”型,仅8个树种为“收益递增”型[8]。
国内关于叶质量—叶面积的投资—收益研究还很少,且没有统一规律。Pan等[9]研究了天目山121种维管植物叶质量—叶面积的关系,随海拔升高植物叶片大小呈“收益递增”型逐渐过渡到“收益递减”型。而Sun等[10]研究表明5种竹类叶片全部符合“收益递减”假设。祝介东等[11]研究我国东部6个地区97种森林植物之间叶面积与叶质量呈“收益递减”型异速生长关系,但各地区之间的异速生长关系斜率差异不显著,均呈等速生长,即“收益稳定”型。姚婧等[12]详细研究了北京东灵山不同林型五角枫(Acermono)不同发育阶段的叶面积与叶质量的异速生长关系,发现成树呈“收益递减”型异速生长关系,但幼树和幼苗呈“收益稳定”的等速生长关系,反映不同生长发育阶段所处的光环境差异影响叶的生长对策。刘辉等[13]建立了天山北坡4种典型草原植物叶面积与叶干重的回归模型,但没有涉及成本-收益假说。
园林绿化树种多为人工引种和栽培,研究物种内的叶片投资—收益关系有助于选择适合度高的园林绿化种[8]。本研究选择帽儿山常见的8种园林绿化木本植物,用叶面积与叶质量的关系以及SLA随叶面积和叶质量的变化规律阐明植物叶片的种内种间变异,在种内和种间尺度检验叶片投资—收益理论。
1 材料与方法
研究地点位于东北林业大学帽儿山实验林场。气候为大陆性气候,年平均气温3.1 ℃,年均降水量723 mm。于7月末每个树种选取3~5株健康成年树木(水曲柳选择幼树),每株树按照大、中、小各选取小叶作为试验单元,采集时尽量涵盖较大和较小的叶片,以便更好地建立叶片面积与质量的异速生长关系。将采集的小叶装入塑料袋,采集完后尽快返回实验室,用扫描仪获取每个叶片的图像(300 DPI),用于计算叶面积(0.001 cm2)。叶片扫描后装入信封于70 ℃烘干48 h后称干质量(0.01 g)。
受大小影响的植物功能性状之间的变异,主要通过对数转换的普适指数模型来检验[1]:
lgA=lgβ+αlgM
lg表示常用对数转换。α<1,“收益递减”;α> 1,“收益递增”;α= 1,“收益稳定”[1,7]。不同树种之间α及其与1差异显著性水平采用似然比检验(likelihood ratio test)。lgβ为截距,即标准化常数。用中位数表达种间SLA与叶大小及面积—质量异速生长回归系数的关系,因为所采集的50个样本并不一定符合正态分布,而中位数是一个更为稳健的统计量。SMA回归斜率差异性检验采用SMATR 2.0软件[14]完成。用SPSS 19.0软件进行单因素方差分析和Turkey多重比较检验叶片面积、叶片质量、比叶面积在8个树种之间是否具有差异性(P= 0.05)。
2 结果与分析
2.1 叶质量、叶面积和比叶面积种间差异
帽儿山8个常见绿化树种的叶质量、叶面积和SLA均存在显著差异(P< 0.01,表1)。其中叶面积水曲柳(53.77 cm2)最大,鸡树条荚蒾(43.24 cm2)次之,而金银忍冬叶片(25.81 cm2)最小。SLA则为梣叶槭(256.93 cm2g-1)最大,紫丁香(146.99 cm2g-1)最小。

表1 帽儿山8个常见绿化树种的平均叶质量、叶面积和比叶面积(SLA)比较
括号内数字为标准误,不同字母表示Turkey HSD显著差异组别(P= 0.05)。

图1 帽儿山8个常见绿化树种的对数坐标下叶面积与叶质量异速生长关系散点图与叶质量异速生长关系散点图
2.2 叶面积与叶质量的异速生长关系
总体上种内和种间叶面积与叶质量均呈斜率小于1的异速生长关系。8个树种的叶面积与叶质量呈显著的线性关系(图1)。表1给出了8个树种和跨树种的叶面积与叶质量异速生长关系比较结果。树种之间的斜率差异显著(P< 0.001)。其中,稠李最高(0.94),其次为白桦(0.93),二者均临界显著低于1(P值分别为0.050和0.047),其余树种的斜率均显著小于1(P< 0.001)(表2)。而截距表现为稠李最高(2.34),花盖梨最低(1.95)。8个树种平均斜率为0.81,截距为2.14。跨树种尺度上,斜率仅为0.63,截距为1.98,均低于混合所有数据所得的0.77和2.10,表明混合种内和种间数据的回归方法受较大叶片的影响而产生偏差。
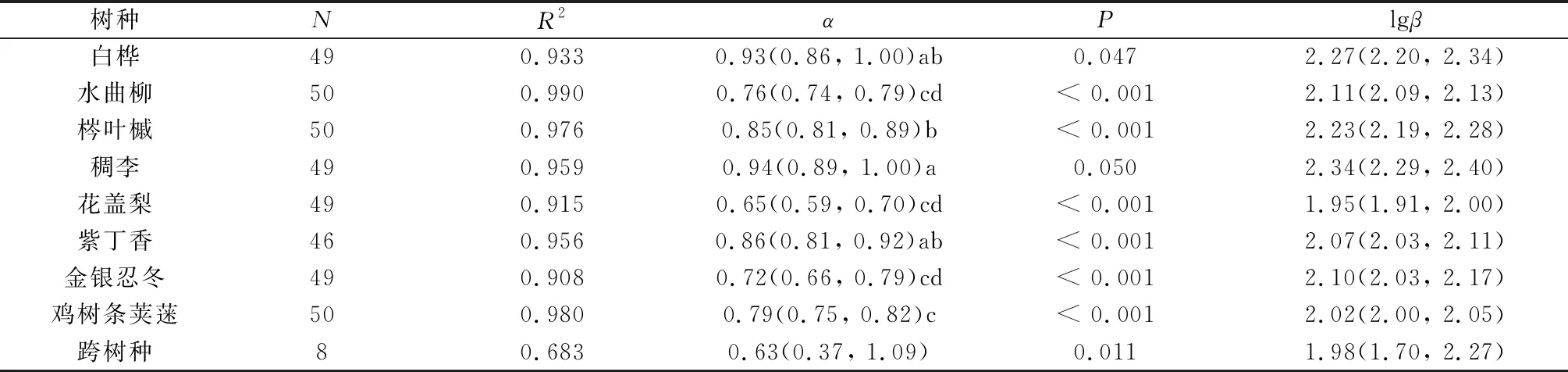
表2 帽儿山8个常见绿化树种的叶面积与叶质量标准主轴回归参数(斜率α和截距lgβ)比较
所有回归均极显著(P≤0.001),不同字母表示显著差异组别(P= 0.05)
2.3 比叶面积随叶片大小的变化
在物种尺度上,SLA均随叶片增大呈负指数函数而降低,降低主要发生在小叶区域(图2)。白桦SLA随叶质量增加有微弱降低趋势(图2a),而随叶面积增大降低不显著(图2b)。此外,除稠李外,各树种叶质量的负指数函数关系比叶面积的更紧密(R2大)。
种间尺度与种内尺度的规律相似。各树种SLA也与叶质量中位数呈负指数函数关系(图3a),但与叶面积中位数的关系不显著。此外,各树种SLA中位数均与叶面积与叶质量标准主轴回归斜率(α)和截距(lgβ)呈正相关关系(图3c和d)。
3 讨论
本研究8个树种叶面积与叶质量的异速生长斜率均小于1,而且SLA也总体上随叶质量增大而降低,表明8个树种的叶片均符合“收益递减”型。如果叶质量包含叶柄,“收益递减”可能进一步增大[15]。本研究8个树种叶面积与叶质量的平均异速生长斜率(0.81)表明叶质量增长比叶面积快,略低于Milla和Reich[7]全球157个物种的平均值(0.87),跨物种的斜率(0.77,基于所有样本)处于全球数据最低水平(0.77~1.42)[7]。这可能是本研究区域的年均温较低(3.1 ℃)有关。大叶片单位叶面积的成本比小叶片的高,据此可以推测本地区的植物适宜较小的叶片。事实(表1)也证明了这一推测。大叶片需要的构建成本更高,是因为他们需要自我支撑和抵抗风力而需要更多地机械支持构件,因此在生长季较短的北方地区大多分布叶片较小的树木。这一规律也对园林绿化树木选择有一定指导意义。
同一植物在不同生境可能导致不同的叶面积—质量异速生长关系,SLA也不同。例如,本研究与辽西的3个树种[8]相比,水曲柳的叶面积-质量异速生长斜率(0.76)大于辽西值(0.41),紫丁香的(0.86)也大于辽西值(0.53),但花盖梨(0.65)小于辽西的(0.95)[8];而3个树种的SLA则为大小顺序呈相反趋势,即帽儿山的花盖梨大于辽西的,水曲柳和紫丁香则为帽儿山的大。同种植物,干旱地区的SLA更小,本研究地年降雨量(723 mm)高于阜新市(539 mm)[8]。花盖梨的反常尚不能给出令人满意的解释,可能是由于阜新市年均温比帽儿山的更低的缘故(0.5 vs. 3.1 ℃)。本研究梣叶槭斜率略小于梣叶槭(原产北美,我国北方较为常见的绿化树种)在原产地的叶面积—质量异速生长斜率0.93(0.78, 1.05; 95%CI)[7],但本研究的SLA(256.93 cm2g-1)比原产地的(152.41 cm2·g-1)[7]大。

图2 帽儿山8个常见绿化树种叶面积与叶片质量的关系
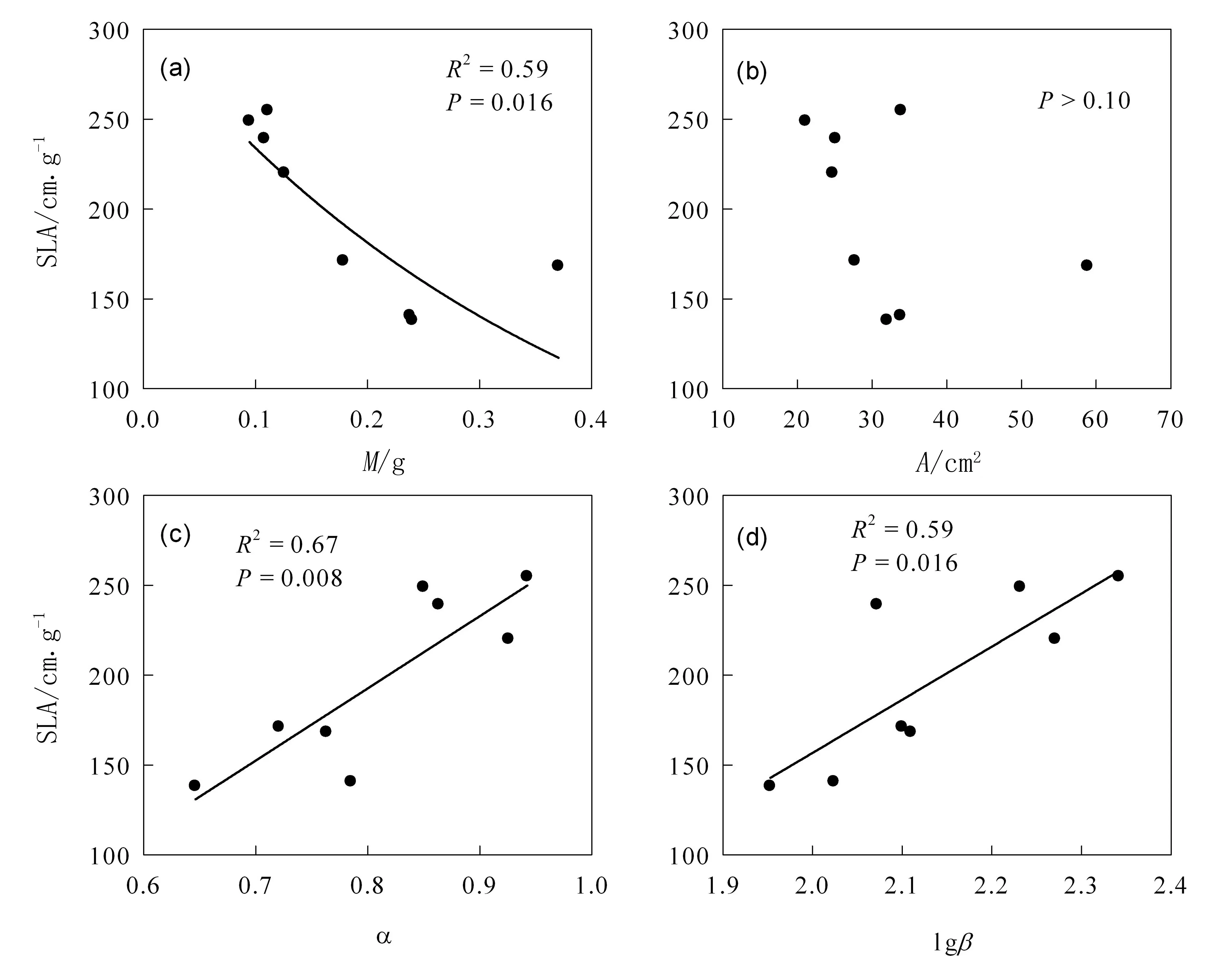
图3 帽儿山8个常见绿化树种的比叶面积中位数(SLA)与叶大小(a)以及叶面积(b)与质量标准主轴异速生长斜率(c)截距(d)的关系
为了阐明关于叶质量的叶片光截获成本的本质,有必要研究种内异速生长关系[7]。但迄今为止,种内叶片投资—收益研究并不多。大部分研究发现种内成熟植物的叶片为“收益递减”型,尽管有部分“收益稳定”型和少数“收益递增”型[7,8,10,12]。“收益递增”预测植物倾向于生长大叶片,但与植物叶片不可能无限生长相悖。多种因素会导致这种结果,首先,取样时采集了萌生枝条的叶片,这些叶片数量在整个树冠上极少,但叶面积大,叶厚度低,一般SLA较大。这些叶片会由于杠杆效应增大SMA回归斜率,与模拟误差结果[7]相符。其次,取样的样本容量过小也会影响回归斜率。为了减小样本容量的影响,本研究选择50个叶片检验投资—收益关系,一定程度上降低了不确定性。最后,截距也是一个应该考虑的问题。SMATR2.0软件在斜率差异显著的情况下不再检验截距的差异性。但本研究发现,SLA与斜率和截距都存在正相关关系(图3c和d)。Sun等[10]发现5个竹类植物之间叶面积与叶质量异速生长截距与平均叶面积正相关(尽管不显著),而与海拔负相关。这些发现暗示,在研究叶片投资—收益种间变异时,仅考虑异速生长斜率的影响是不够的,还要考虑异速生长截距的作用。
