平移算子的微分多项式的零点分布的再研究

别荣军

(安徽建筑大学 数理学院，安徽 合肥 230601)

1 引言及主要结果

本文所用到的值分布论中的标准符号和基本内容同参考文献[1-2]一致。S(r,f) 表示任意满足S(r,f)=o(T(r,f))的量，可能除去r的一个线性测度为有限的集合。若亚纯函数a(z)满足T(r,a)=S(r,f)，则称 a(z)为 f(z)的小函数。

最近三十年来，涉及微分或差分多项式的亚纯函数的值分布以及惟一性问题的研究取得了很好的成果。2012年，刘凯[3]等人研究差分微分多项式的零点分布，得到了

定理1[3]设f(z)非周期函数，而是有穷级的超越整函数， α(z)为f(z)的小函数。若n≥k+3，则[f(z)nΔcf](k)-α(z)必有无穷多个零点。

2019年，Laine[4]研究了涉及平移算子的多项式的值分布，得到了

定理2[4]设f(z)是有穷级ρ的超越整函数， α(z),b1(z),b2(z),…,bl(z)为f(z)的非零小F=[f(z)nψs(f)]- α(z)必有无穷多个零点，且λ(F)= ρ。

本文讨论涉及平移算子的微分多项式的值分布情况，得到如下结论：

定理3 设f(z)是有穷级ρ的超越整函数，α(z),b1(z),b2(z),…,bl(z)为f(z)的非零小函数，常数。若正整数n,s满足 n≥2k+s+3,s≥1，则[f(z)nψs(f)](k)-α(z)必有无穷多个零点，且其级为ρ。

定理3的结论从另外一种形式改进了定理1，并且将定理2的结论推广到微分多项式的情形。

2 引理

为了证明我们的结论，在此先介绍几个引理。

引理1[5]假设f是一个具有有穷级ρ的亚纯函数， c为非零常数，则对任意的ε＞0，有

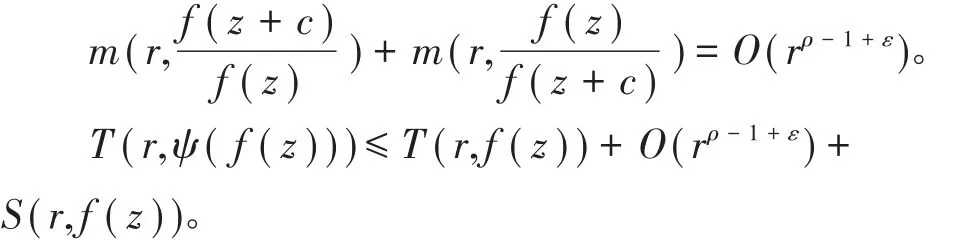
引理2 假设f是一个具有有穷级ρ的整函数， ψ(f(z))如定理3给出。则

T(r,ψ(f(z)))≤ T(r,f(z))+O(rρ-1+ε)+S(r,f(z))。

证明：由第一基本定理与引理1，得到

≤ T(r,f(z))+O(rρ-1+ε)+S(r,f(z))

引理3 设f是一个具有有穷级ρ的超越整函数， ψ(f)如定理3给出，F(Z)=fn(z) ψS(f)且n,s,k为正整数，则

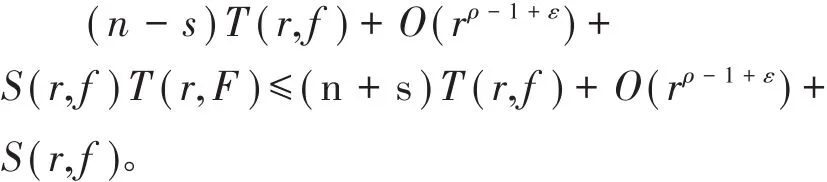
证明：注意到f是整函数，

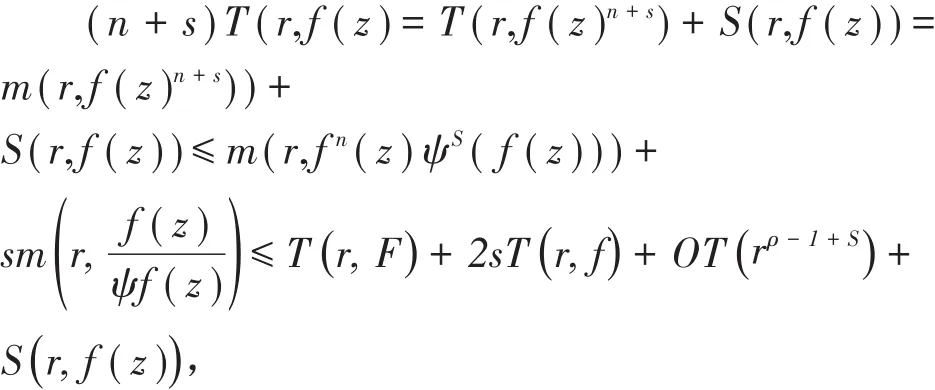
即

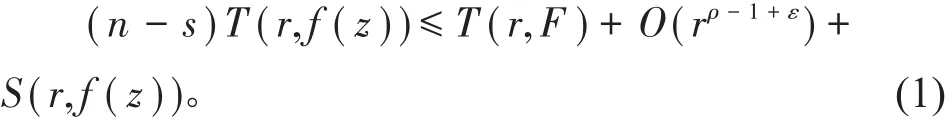
另一方面，由引理1与第一基本定理得到

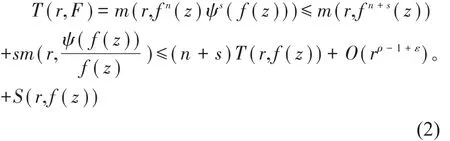
由式(1)与式(2)可知结论成立。

引理4[1]假设f是亚纯函数， P(z)为一n(≥1)次多项式， 则有

T(r,P(f))=n T(r,f)+S(r,f)。

引理5[1]假设f(z)为定义在ℂ上的亚纯函数， 且 α1(z),α2(z),α3(z)是 f(z)的三个互不相同的小函数， 则有

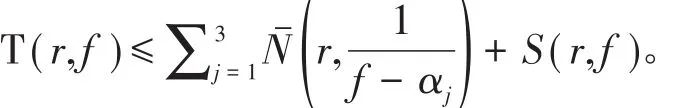
引理 6[6，7]假设 f(z)是非常数亚纯函数，p,k为正整数。则

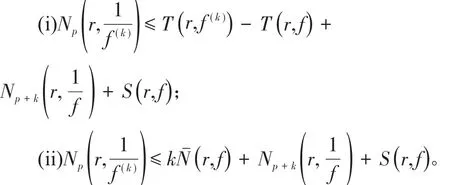
引理7[1]假设是一个非常数亚纯函数，F(z)=fn(z)ψs(f)为正整数，则 F(z)=fn(z)ψs(f)与F(z)=fn(z)ψs(f)有相同级和下级。

3 定理的3证明

假设F(z)=fn(z)ψs(f)。由定理2的证明过程可知，ρ(F(z))=ρ。由引理7得到ρ(F(k)(z))=ρ(F(z))。注意到 ρ(F(k)(z)- α(z))= ρ(F(k)(z))，所以ρ(F(k)(z)-α(z))=ρ。

假设F(k)(z)-a(z)只有有限个零点。由引理2知，F(z)不是常数，且S(r,F(k)(z))=S(r,F(z))=S(r,f(z))。将引理 5 作用于 F(k)(z)，有

结合式(4)，由引理2，引理3与引理4得到

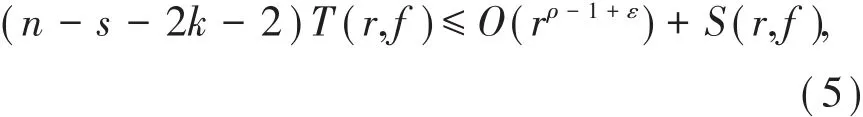
式(5)与条件n≥2k+s+3矛盾。完成定理3的证明。