“正交分解”在高中物理习题中的应用

福建省安溪铭选中学 林泽炜

一、基本模型分解力

正交分解，是指把力沿着两个选定的相互垂直的坐标轴方向加以分解的方法，通过必修1的教学，学生已能使用正交分解分析水平面、竖直面和斜面上的物体，正交分解模型基本确立。

二、活化模型分解运动量

经典问题1：用一根长为L的细线一端系一小球(可视为质点)，另一端固定在一个光滑锥顶上，如图所示，锥面与竖直方向夹角为θ，小球沿着锥面在水平面内做向心加速度为a的匀速圆周运动，若小球未离开斜面，试分析细线的张力FT和锥面的支持力N与a的关系。

本问题是要利用牛顿第二定律分析物体的圆周运动，按常规思路，应将力沿平行半径和垂直半径的方向进行分解，做法如下：

方法1：如图甲，

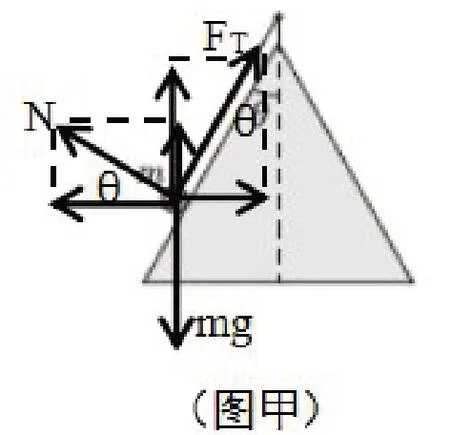
水平：FT·sinθ-N·cosθ=ma①

竖直：FT·cosθ+N·sinθ=mg②

①×sinθ+②×cosθ得：FT=masinθ+mgcosθ

②×sinθ-①×cosθ得：N=mgsinθ-m·acosθ

这种方法格式固定、容易理解，但由于涉及比较巧妙的数学运算，方程不易求解。如果这是一道选择题，会列方程却不会求解，做了也白做。根据独立性原理，某方向上的力只会产生该方向上的加速度，这给我们分析问题提供了又一思路。

方法2：如图乙，

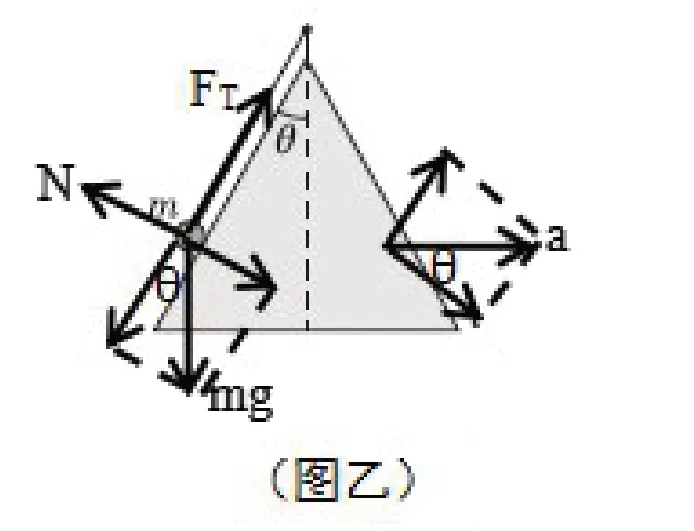
沿锥面：FT-mg·cosθ=m·asinθ

垂直锥面：mg·sinθ-N=m·acosθ

移项即有：FT=masinθ+mgcosθ

N=mgsinθ-m·acosθ

这里，将力和向心加速度同时沿平行斜面和垂直斜面进行分解，分方向列出牛顿第二定律后，移项即可得出答案。对于“斜面上”的物体，如果加速度沿水平或竖直方向，在分解力的同时“按需”分解加速度，往往能化繁为易，减小运算量。

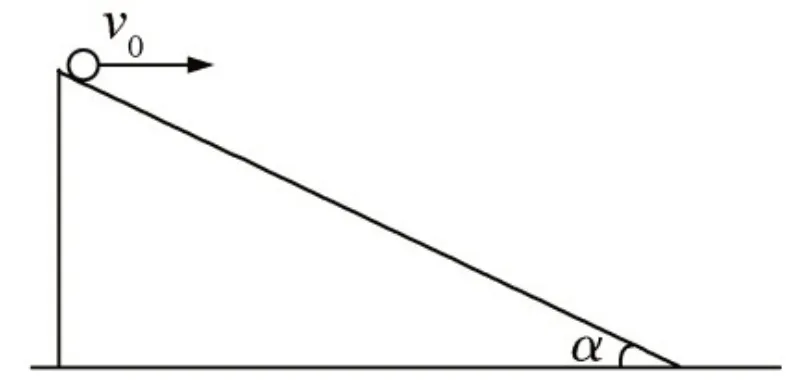
经典问题2：水平面上固定一个倾角为α的斜面，将一个小球从斜面顶端以速度v0水平抛出，不计空气阻力的影响，经过时间t小球落在斜面上，求在这一运动过程中小球距斜面的最远距离hm=?

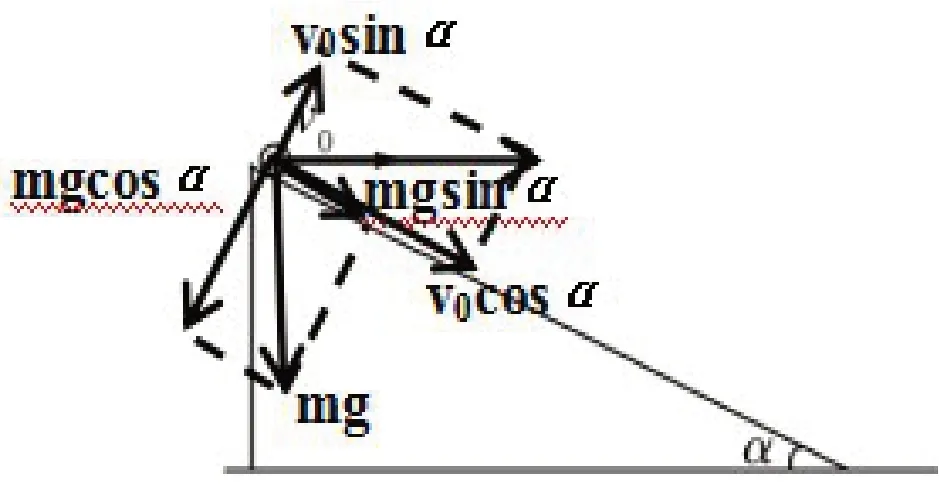
分析做平抛运动的物体时，正交分解因其“化曲为直”的优点而被广泛使用。本问题中，如果采用常规思路，把平抛分解为水平方向的匀速直线运动和竖直方向的自由落体，我们很难找出最远距离同平抛的水平位移和竖直位移之间的几何关系。如果把重力和初速度均沿平行斜面和垂直斜面进行分解，根据运动的等效性，平抛可视为平行斜面的匀加速直线运动（a1=gsinα）和垂直斜面的匀减速直线运动（a2=gcosα）的合运动，容易发现：当垂直斜面的分速度减小为0，即：

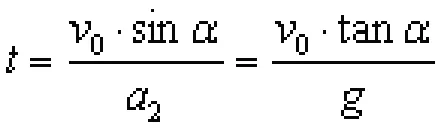
这时，物体离斜面最远，这个最远距离恰好等于物体在该方向匀减速到0时前进的位移，即：

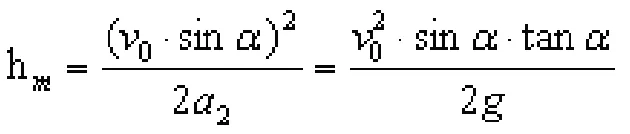
像“物体在某个方向运动（这个方向称为x方向，与之垂直的方向称为y方向）的最大距离”一类的问题，把力和速度同时沿x 方向和y 方向进行正交分解，抓住沿x方向减速到0的特征，思路就比较清晰。

三、深化物理模型分解电场强度

经典问题3：如图所示，A、B、C、D、E、F为匀强电场中一个边长为1m的正六边形的六个顶点（匀强电场和六边形所在平面平行），B、C、F三点电势分别为1 V、2 V、3 V，该匀强电场的场强大小为______V/m。

大众印象中，正交分解只是分析动力学问题的“利器”，但实际上它也是解决其他矢量问题的有力工具。比如，匀强电场中，根据电场的特性，水平（竖直）方向的电场在竖直（水平）方向上不会产生电势差，如果将电场正交分解为水平（x方向）和竖直（y方向）两个相互垂直的方向的电场Ex 和Ey，那就可以理解为水平（竖直）方向的电场产生水平（竖直）方向的电势差，于是有：Ex=Ux/dx；Ey=Uy/dy，其中Ex、Ux、dx（Ey、Uy、dy）分别对应x方向（y方向）上两点间的电场强度、电势差和距离。

本题中，因UC-UB=UE-UF，则UE=4V；FC连线中点的电势为U0=UCF/2=2.5V，则由UO-UC=UE-UD可知UD=3.5V，由UA-UB=UE-UD可知UA=1.5V；若将电场沿DC方向和DF方向进行正交分解，容易求得：

水平分电场：

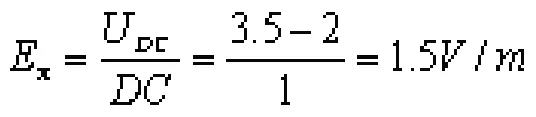
竖直分电场：

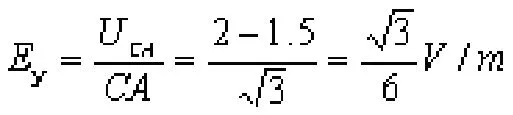
再根据矢量合成容易得出总电场强度：

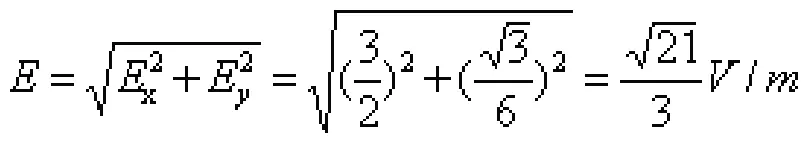
可见，正交分解法有助于学生深入理解匀强电场U=Ed这一规律的本质特征，对于分析已知某三个点电势的匀强电场的场强，能有效避开复杂的几何分析。

四、结语

正交分解加速度、速度和电场强度，根据需要分解不同的物理量，选择不同的分解方向，这种“按需”分解对于解决诸多矢量问题往往有事半功倍的奇效。这些问题的解决，活化了正交分解的方法，深化了正交分解的模型，丰富了正交分解的内涵，也推动了科学思维这一学科核心素养的有效渗透。