降水量突变对汾河流域汛期影响研究

段 州

（晋城市郭壁供水工程管理处 山西晋城 048000）

0 引言

汛期分期是根据暴雨洪水在不同时期所表现出的差距进行划分的[1]。科学的汛期分期是水库调度的前提，对于流域、水库防洪及水资源的合理应用等具有重大意义[2]。近百年来全球气候变暖，导致降水量时空分布发生改变[3-4]。在水库调度运行中，降水量是决定汛期时间节点的关键因素，降水量时空分布的改变会引起汛期分期的变化，而现行的汛期分期是根据多年降雨资料获得的，缺乏了对降水量变化条件的考虑[5]。因此本文以汾河流域为研究区，首先采用CSD趋势分析法对汾河流域降水量突变点进行了检验，并分别以突变年前后的时间序列为基础，对汾河流域进行了汛期分期，研究降水量时空分布变化对汾河流域汛期时间节点变化的影响。

1 理论基础

1.1 趋势检验法

趋势检验（Cumulative Sum of rank Difference，CSD）利用了图形诊断和统计分析，由Charles Onyutha于2017年提出，且已经被很好地应用于评估水文气象学的变化[6-8]。因此，本文采用CSD检测法对汾河流域降水量变化趋势进行检验。具体步骤如下:

1）X表示已知的数据系列，则时间序列Y可以通过对X进行复制得到。则可以得到数据点的超越和非超越计数的重标时间序列c。

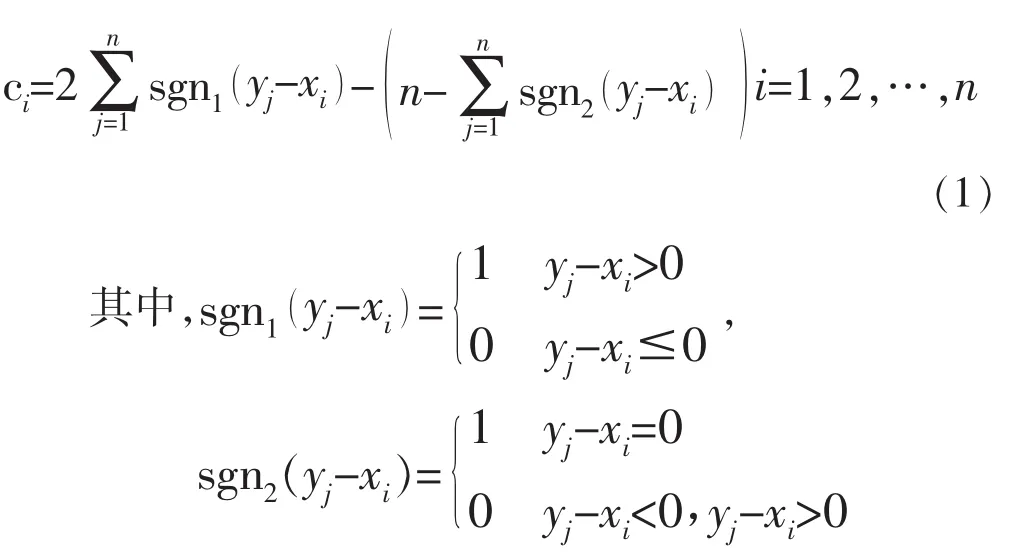
2）计算趋势统计TCSD。

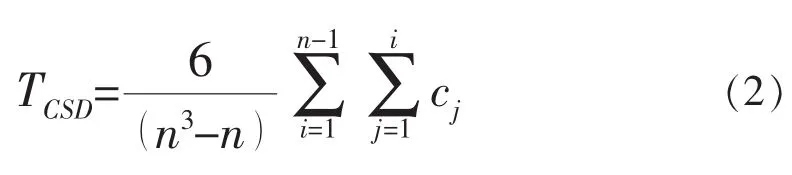
TCSD的正/负值表示上升/下降的线性趋势。TCSD的分布与Onyutha所给出的零和方差（V1）的均值近似接近正态分布:

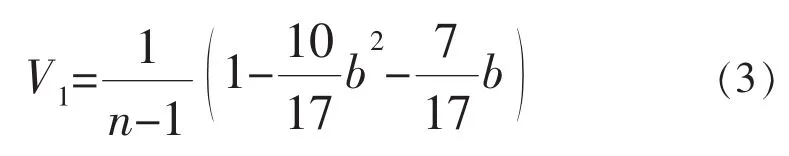
其中b是数据中联系的度量:

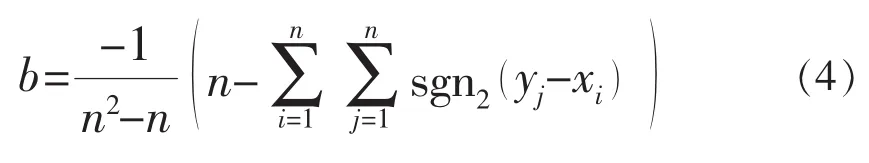
Zαs/2作为αs%下的标准正态变量，ZCSD表示标准趋势统计量，其均值服从标准正态分布，方差等于1。如果|ZCSD|≥|Zαs/2|，则H0（无趋势）在αs%下不显著，否则H0在αs%显著。

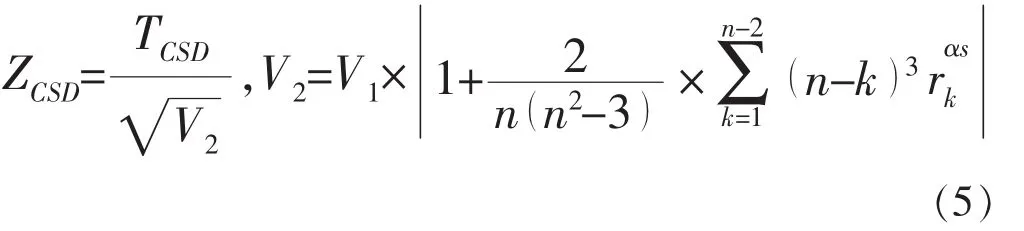
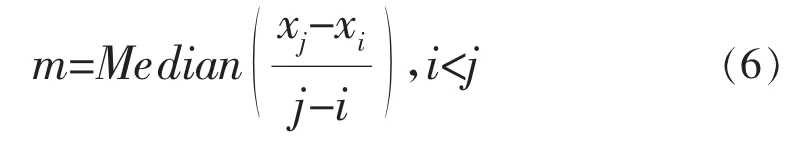
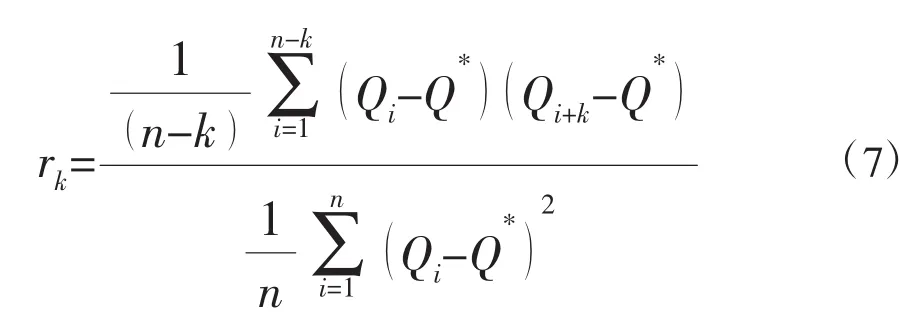
用于检测rk显著性的（100-αs）%置信区间CL可以用下式计算:

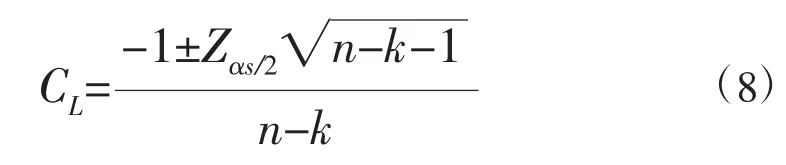
累积和（Csum）可由方程（2）中的c获得:

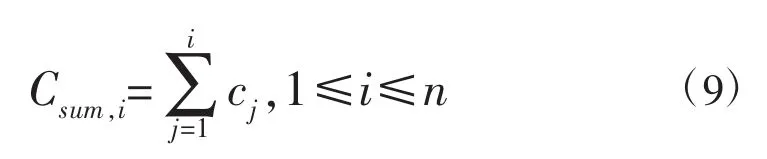
从图形上说，Csum，i可以依据i或者观察时间来绘制来识别系列中的变化。

1.2 汛期分期的量变质变判别模式

步骤1.构建n个指标特征值矩阵X:

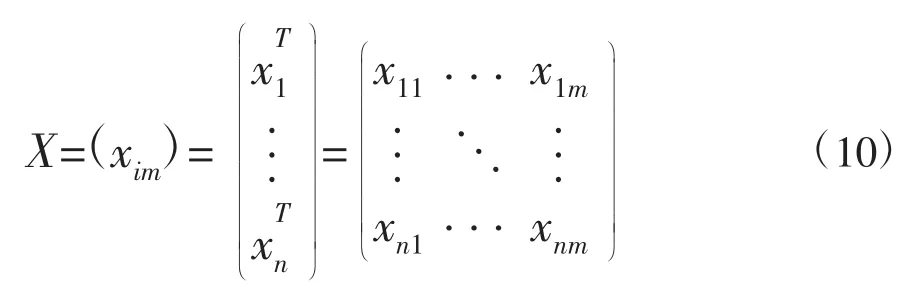
其中xnm为时序m指标n特征值。

步骤2.确定时序研究对象ut指标i的特征值xim落入汛前期与主汛期或主汛期与后汛期相对隶属度为 1的标准值区间矩阵［Ni1，Ni2］，已知矩阵 X，可得标准区间矩阵Y:

Y=（Nih），其中i=1，2，3…n；h=1，2

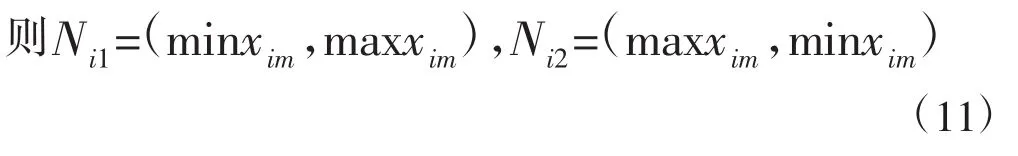
其中:maxxim，minxim分别为时序集xim的最大、最小特征值。

步骤3.计算xim落入 ［Ni1，Ni2］区间的相对隶属度:

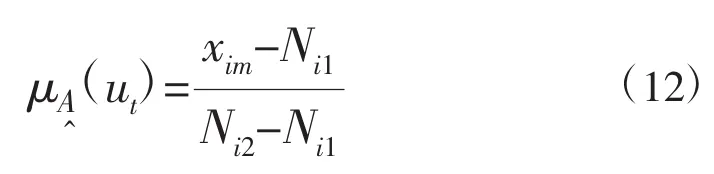
步骤4.根据主成分分析法确定各指标的权重wi。

步骤5.计算ut综合相对隶属度:

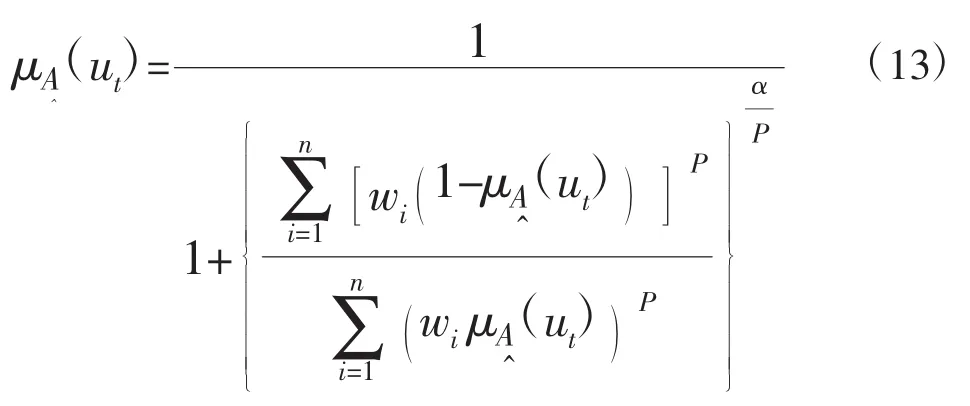
式中:α为优化准则参数，P为距离参数。α=1为最小一乘方优化准则，α=2为最小二乘方优化准则；考虑到α=2对距离具有放大或缩小效应，因此，在汛期分期的应用中，选取α=1。

若采用优化准则参数α=1，距离参数为海明距离，即P=1，则式（13）变为线性公式:

若汛期分期为非线性系统，可采用欧氏距离，即P=2，式（13）变为:

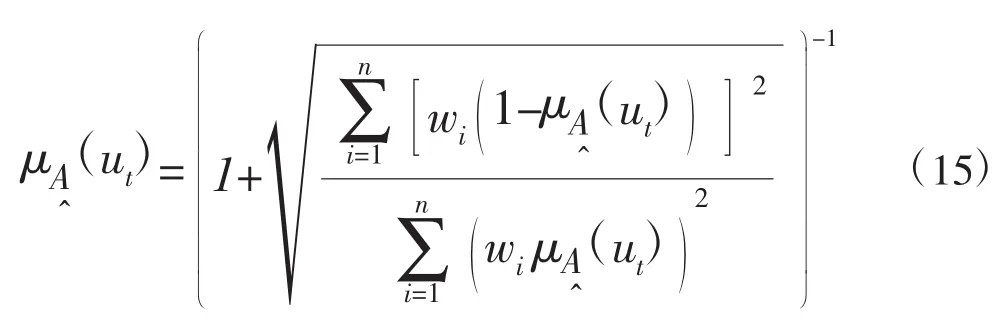
步骤6.计算P=1和P=2的两种情况下的ut平均综合相对隶属度

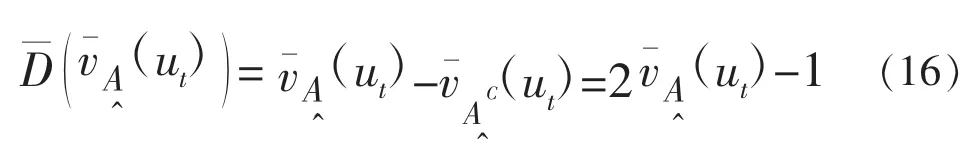
步骤8.应用质变与量变判别模式分析汛期演变规律。

1.3 方差评价指标建立

以往人们对汛期分期理论方法进行了许多研究，但对分期结果的评价研究却很少。本文提出了考虑权重因子的均方误差S的评价指标。评价指标S可以通过以下步骤来计算:

步骤1:将n视为样本的研究年数，选择xij作为检验结果的指标（一般选择日降水量或者径流量），其中i是代表汛期中的某一天，j代表汛中的某一年。如果mk代表第K个分期距汛期开始时间的长度（天），则mk+1代表第K+1个分期的长度（天），即若mk代表汛期开始时间到前汛期截至天数，则mk+1代表汛期开始时间到主汛期截至时间。则当n=1时，即只对一年的汛期结果进行评价，则n=1时每个分期的标准偏差S可以表示为:

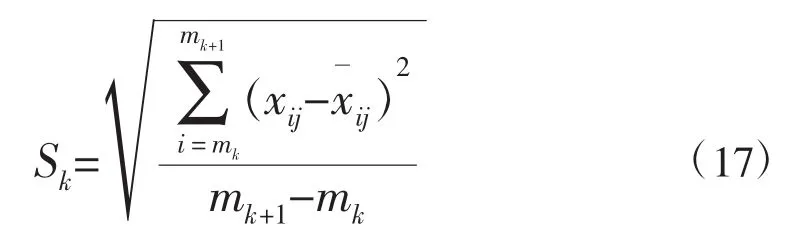
步骤2:设q为分割点数，则q+1为分段数，λk为与第k个汛期相对应的权重因子，可根据不同汛期的重要性进行设置。某一年的汛期分期标准差可以表示为:

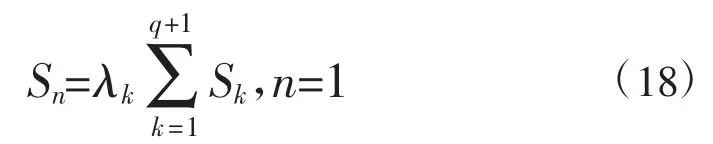
步骤3:当研究样本为多年时，即n≠1，则评价指标S可以表现为以下形式:

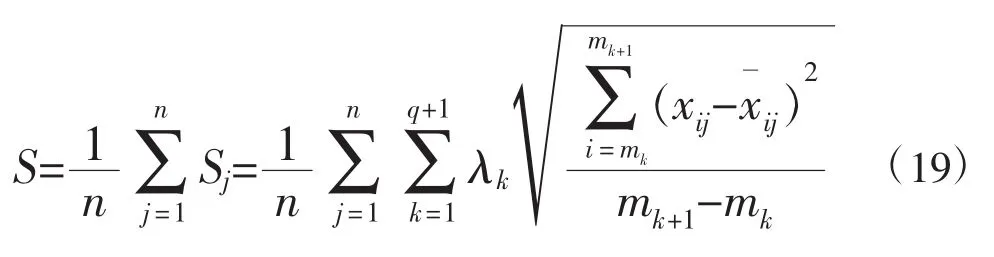
2 汾河流域降水量时空变化

汾河是山西省最大的河流，本文所用基础气象数据来源于中国气象科学数据共享服务网，由1957-2014年汾河流域13个气象站资料加权得到汾河流域的面降水量。用CSD法检测汾河流域1957-2014年降水量的突变年，结果如图1所示，以Csum=0线为参考。累积和从参考值的偏差表征了该系列中的时间变化。当系列值的子周期的时间序列以随机变化为特征，则在另一部分具有线性趋势，而在具有线性趋势的部分上将形成曲线的趋势。因此，从图1-（1）重标系列中系列趋势分析可以得到，在各序列之间，以线性递减趋势为特征，该趋势对应图1-（3）中各序列号之间的曲线的趋势。对于线性递增或递减的序列，变点是对应于最大异常值的点，即第29个时间序列。因此，我们可以得出，1957-2014年汾河流域降水量的变化规律，1957-2017年汾河流域降水量呈线性减少趋势，且1985年为汾河流域降雨的突变点。因此，本文将1985年定为汾河流域降水量突变年，分析突变年前后汾河流域汛期的变化。

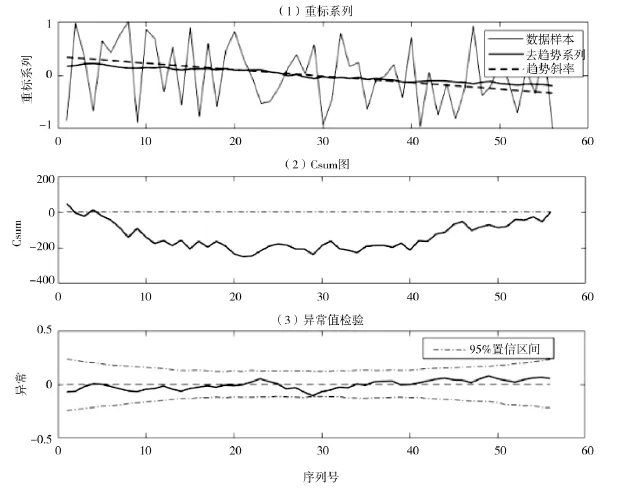
图1 汾河流域降水量序列突变检验

3 汾河流域汛期分期

汾河流域现行的汛期研究域为6-9月，以候（5天）为基本单元对汛期进行划分，将汾河流域汛期研究域划分为24个候，以汾河流域1957-2014年共58年的逐日面降雨资料为基础，选取能够反映流域汛期内暴雨洪水变化特征的4个因子作为影响因子:候暴雨均值、候暴雨Cv值、候最大1 d暴雨、候最大3 d暴雨、候暴雨天数（日降水量大于25 mm）作为汛期分期的指标[9]，进行汾河流域的汛期划分，根据汛期划分指标特征值，得到1957-1985、1986-2014年从前汛期过渡到主汛期和从主汛期过渡到后汛期的平均对立差异度，如表1所示。以1957-1985年为例，可应用量变与质变判别模式对汛期演变过程进行分析:6-9月的第1个候为变化起点到第6个候说明这一时期，指标值发生的都是量变；6-9月的第6-7个候说明综合指标发生了渐变式质变，表明降雨指标变化已经跨过了渐变式质变界，即汛期的演变从前汛期过渡到了主汛期。6-9月的第7-19个候说明期间综合指标发生的是量 变。6-9 月的第 19-20 个候说明综合指标发生了渐变式质变，表明降雨指标变化已经跨过了渐变式质变界，即汛期的演变从主汛期过渡到了后汛期。6-9月的第20-24个候说明期间综合指标发生的是量变。

将平均对立差异度绘制成曲线图，可得到对立差异度为0时的汛期时间节点，对汛期进行划分，如图2及表2所示。可见降水量突变年后的主汛期较突变年前缩短，这与汾河流域降水量减少趋势相符合，降水量减少，则相应的主汛期缩短。

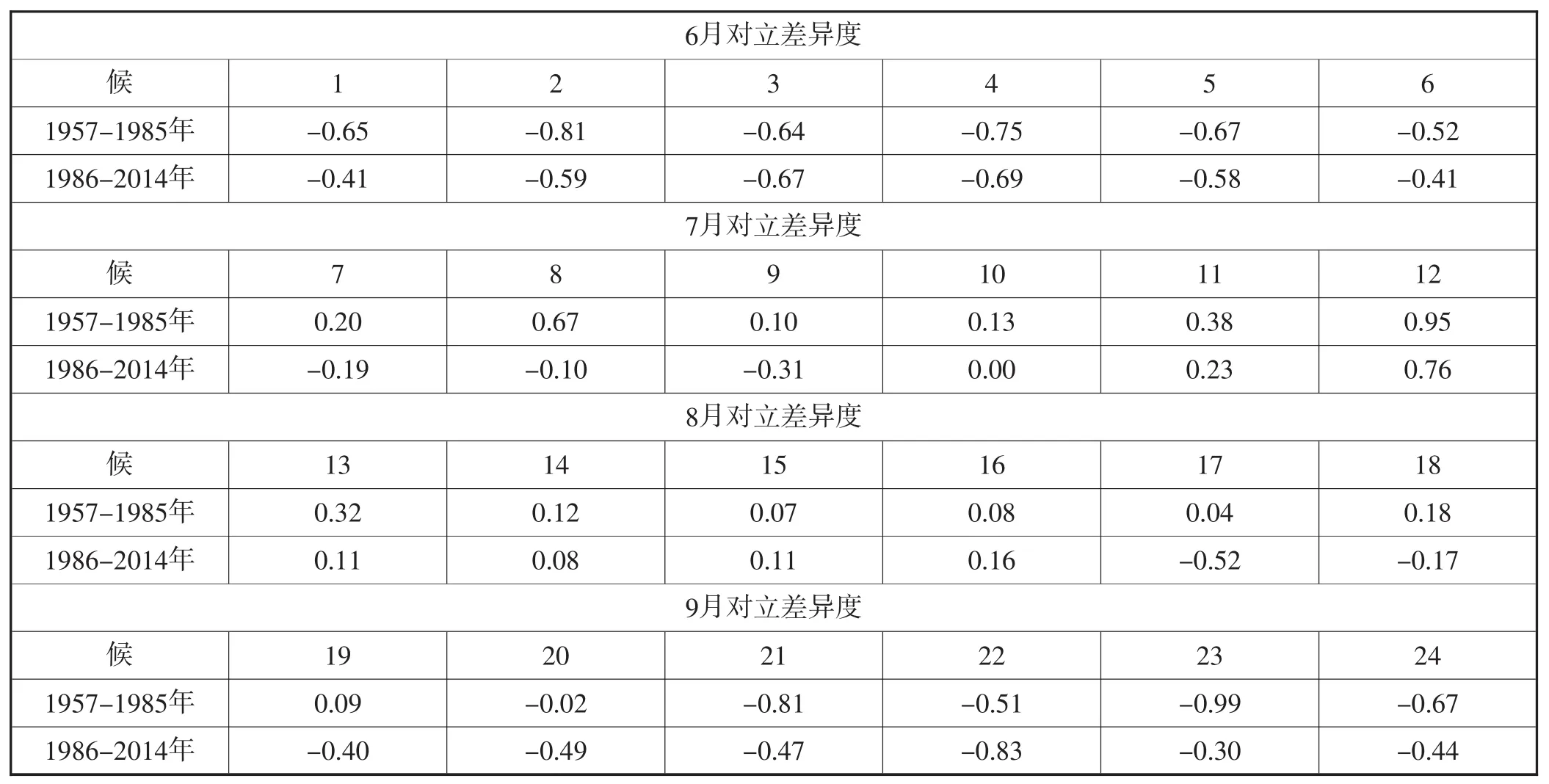
表1 1957-1985、1986-2014年汛期平均对立差异度计算结果

4 分期结果评价

这里选取汾河流域1957-2014年汛期（6.01-9.30）逐日降水量作为汛期流域的特征指标量，在3组不同的权重组合下，求得不同研究时段所得汛期分期结果的评判指标S，其结果见表3。

由表3可知，各分期结果下的1985-2014的S值小于1957-1985对应S值，表明1985-2014年求得的

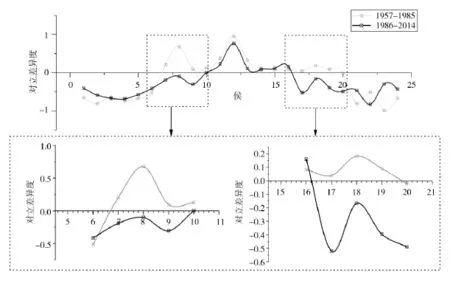
图2 平均对立差异度图

表2 汛期分期结果

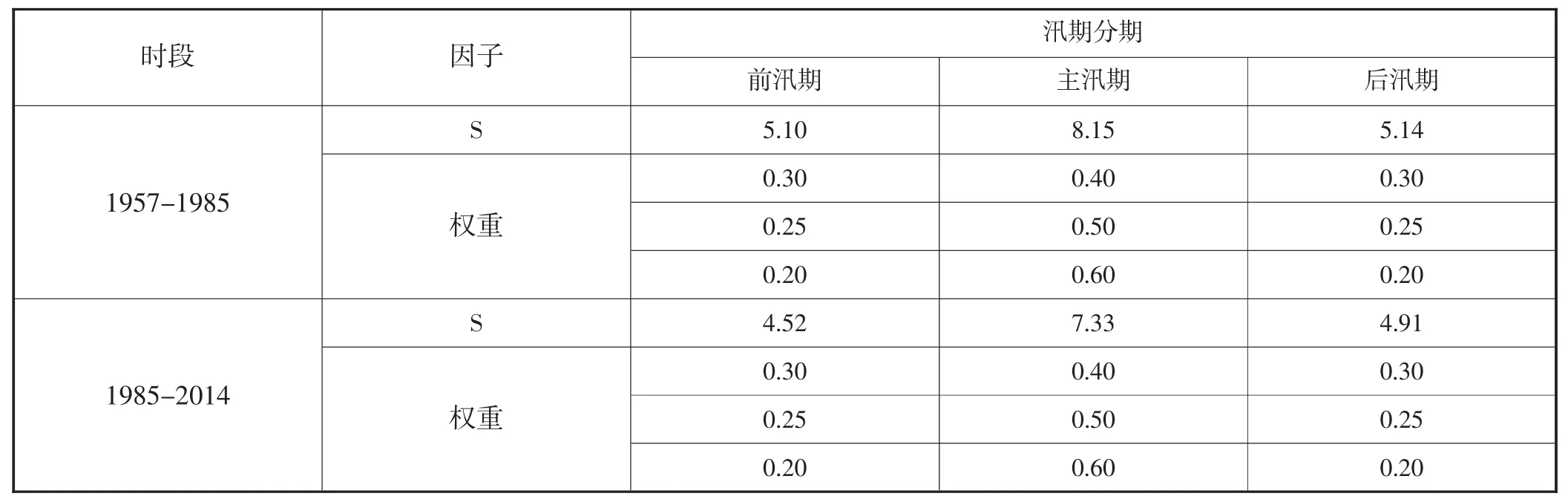
表3 汛期分期结果的评判指标

汛期分期结果较1957-1985精度高，因此，在降水量发生突变以后，以突变年后的时间段作为汛期分期研究域，进行流域汛期分期更能反映实际情况，本文突变年后所得主汛期较突变年前短30天，汛期缩短可以使流域内水库汛限水位维持的时间缩短，水库会提前进入正常蓄水状态，对缺水地区下游人民的灌溉生活等用水产生一定的经济效益[10]，但汛期缩短产生的风险还需要进一步分析，未来需要结合水库的调度对汛期的变化进行合理性分析，也可以将突变年后汛期缩短的时间作为主汛期到后汛期的过渡期，适当抬高汛限水位制定相应的过渡期水位，这样可在考虑降水量时空分布变化的基础上有效降低汛期缩短所产生的风险。

5 结论与建议

通过采用CSD法检测降水量突变点，量变质变判别模式进行汛期划分，得到了汾河流域降水量时空分布变化对汛期的影响，本研究结论可归纳如下:

1）汾河流域降水量于 1985年发生突变，且1957-2014年的年降水量呈线性下降趋势。

2）1986-2014年汾河流域的汛期比1957-1985年的主汛期缩短了30天，突变年前即1957-1985年前汛期为6.01-7.04，主汛期为7.05-9.09，后汛期为9.10-9.30。突变年后即1986-2014年前汛期为6.01-7.16，主汛期为7.17-8.21，后汛期为8.22-9.30。

3）汛期缩短产生一定的经济效益的同时对流域内水库调度也产生了一定影响，未来可以考虑将突变年后汛期缩短的时间作为过渡期，适当抬高汛限水位制定相应的过渡期水位，进行水库汛期调度研究。