带时变计算时间和计算误差的倒立摆视觉H∞控制研究
2019-04-12杜大军占国华李汪佩费敏锐周文举
杜大军 占国华 李汪佩 费敏锐 周文举
倒立摆作为一个支点在下、重心在上的绝对不稳定被控对象,其具有非线性、不稳定等特性[1],能够反映控制理论与工程中很多核心问题,例如鲁棒性、跟踪等,作为理想的实验平台验证的理论方法可推广应用到机器人直立行走的平衡控制、火箭发射中的垂直控制、海上钻井平台的稳定控制等[2−4],故倒立摆的稳定控制一直以来都是控制领域研究中的开放性问题[5−7].
传统倒立摆稳定控制大都基于编码器进行状态信息测量然后进行控制器设计和稳定性分析[[8−11].然而,随着视觉传感技术的跨越式发展并且感知信息更加丰富全面、直观,甚至能够应用到复杂危险的工业控制现场[12−13],故其正在大量地被应用到工业自动化检测[14]、机器人控制[15−16]等领域.然而,在实时控制系统中,与非视觉传感测量相比,为了获得状态检测信息,必须对视觉传感测量的图像进行处理,这将不可避免地带来图像处理计算时间和计算误差,从而影响控制系统性能甚至造成控制系统失稳[17].因此,国内外学者开始构建基于视觉传感的倒立摆控制系统实验平台进行理论方法验证,为工业视觉伺服实时控制提供理论基础和技术支撑.
在倒立摆视觉伺服控制中,因为倒立摆属于快变的运动控制系统,采样周期非常小,故从摆体图像采集到经过图像处理计算出小车位移和摆杆偏角耗费的计算时间对控制系统性能及其稳定性影响至关重要.根据是否考虑图像处理计算时间将目前倒立摆视觉伺服控制研究分为两类:第一类不考虑图像处理计算时间的倒立摆视觉伺服控制.例如文献[18]采用视觉传感仅测量直线一级倒立摆的摆杆偏角,并设计模糊逻辑控制器实现倒立摆的稳定控制.文献[19]选取高帧率(580fps)低像素的工业相机测量旋转式倒立摆的摆杆偏角实现稳定控制.以上研究采用视觉传感仅测量了倒立摆的部分状态信息,然而当全部状态信息采用视觉传感进行采集并进行处理时,产生的计算时间将严重影响控制系统性能甚至造成系统失稳,为此国内外学者已开始考虑计算时间研究倒立摆视觉伺服控制.第二类考虑图像处理计算时间的倒立摆视觉伺服控制.例如文献[20]对直线一级倒立摆视觉图像计算小车位移和摆杆偏角时,计算时间高达60ms,为此采用Smith预估算法进行时延补偿并实现了稳定控制.文献[21]将对直线一级倒立摆视觉图像处理产生的计算时间当作定时滞处理实现了稳定控制.以上初步研究了图像处理计算时间对倒立摆稳定控制影响,但是它直接影响采样策略与系统性能,故不能简单地将其看作普通时延,亟需对视觉传感采样策略、计算时间特性及系统性能开展深入研究.
另外,在倒立摆实时控制实验过程中进一步发现,由于背景、光照及实验环境等导致视觉传感采集的图像带有噪声,使得在计算小车位移和摆杆偏角过程中不可避免地产生计算误差,这对倒立摆控制系统性能也具有较大影响.然而目前关于视觉伺服控制系统研究成果中鲜有考虑图像处理计算误差,因此深入分析图像处理计算误差特性及其对系统稳定性能的影响非常重要.
本文聚焦于倒立摆视觉稳定控制中图像处理带来的时变计算时间和计算误差影响控制系统性能甚至稳定性问题,深入开展倒立摆视觉稳定控制研究,主要贡献包括:1)创新设计了新型的倒立摆视觉伺服控制实验平台,设计了一种基于事件触发机制的工业图像采集策略,提出了考虑小车和摆杆特征的小车位移和摆杆偏角计算方法,并统计分析了图像处理计算时间和计算误差特性;2)建立了融合计算时间和计算误差的闭环控制系统模型,理论证明系统的稳定性并建立了反映计算时间与系统稳定性能之间关系,给出了系统对计算误差的H∞扰动抑制水平γ和H∞控制器设计方法.
1 倒立摆视觉伺服控制实验平台
为了分析图像处理计算时间和计算误差对控制系统性能的影响,以倒立摆运动控制实验装置为基础,采用视觉传感代替传统编码器,创新设计了一种新型的倒立摆视觉伺服控制实验平台,结构如图1所示.在实验平台中,工业相机首先采集倒立摆实时运动图像,然后传送到图像处理和控制单元,经过图像处理计算得到摆杆偏角和小车位移的状态信息,接着通过控制算法求出控制信号并发送到运动控制卡,实现控制信号到控制脉冲量的转换,最后由伺服驱动器带动伺服电机转动控制小车运动,实现倒立摆视觉实时反馈控制.
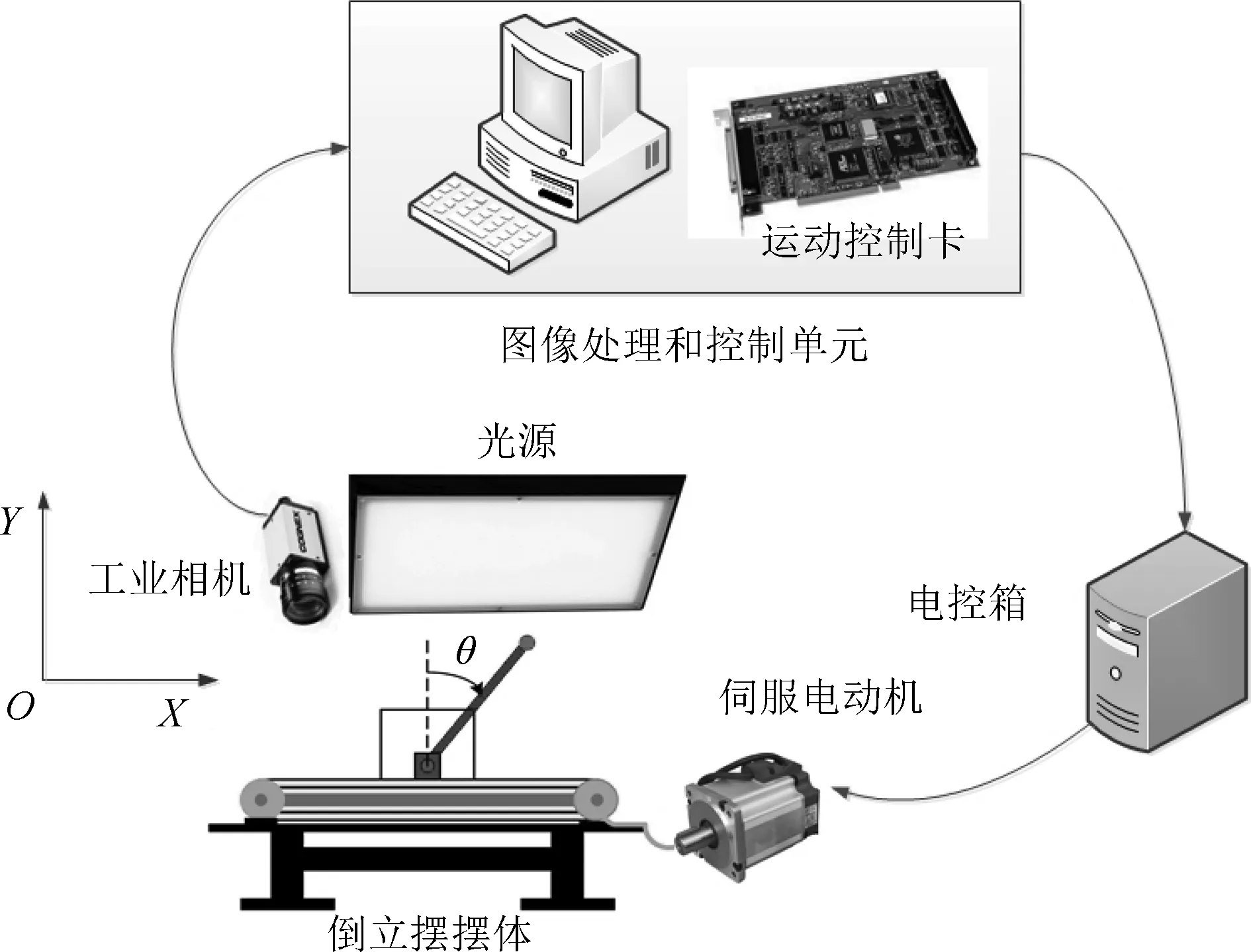
图1 倒立摆视觉伺服控制实验平台结构Fig.1 Scheme of inverted pendulum visual servoing control platform
图1中的实验平台主要包括以下几个部分:
1)摆体.选取直线一级倒立摆作为被控对象,由基座、小车、摆杆、滑轨、同步带、交流伺服电机、伺服驱动器、光电编码器和限位开关组成.轨道长度0.6m,铝制摆杆长0.5m,摆杆通过联轴器铰链在小车上,并且摆杆可自由旋转.
2)视觉传感检测装置.主要包括工业相机和光源,工业相机采用Aca640-120gm 型单色相机,帧率可以自由调节,最大帧率为120fps,图像采集最大分辨率为659×492像素.光源自主设计采用5根纵向排列的LED日照灯管,架设在摆体正上方,光源与摆体之间高度可以自由调节,同时可以根据实际需求自由调节光照强度.
3)图像处理和控制单元.为了处理视觉传感器采集的图像,基于一台带有操作系统Windows XP的PC机,采用Microsoft Visual Studio 2010结合OpenCV2.4.11机器视觉库研发了一套倒立摆图像处理软件,能运用多种算法处理倒立摆图像,计算摆杆偏角和小车位移,然后根据控制算法计算控制信号,并发送到安装在PCI插槽中的GT-400-SV-PCI型运动控制卡,通过其输出相应的控制脉冲量.
4)执行器.主要包括交流伺服电机驱动器和伺服电机,运动控制卡下发给伺服电机的控制信号,通过伺服电机驱动器驱动伺服电机,然后通过皮带带动小车在轨道上来回运动.
在以上建立的倒立摆视觉伺服控制系统实验平台中,摆杆偏角和小车位移状态信息的测量是实现系统稳定控制的前提与基础.然而,当视觉传感取代编码器后,无法通过图像直接读取小车位移和摆杆偏角,必须先对摆体图像进行处理与定位,然后计算小车位移和摆杆偏角,但是在该过程中不可避免地产生计算时间和计算误差两个关键问题.
1)计算时间.由于倒立摆属于快变的运动控制对象,文献[2]采用编码器进行状态信息采集并设置采样周期为T=10ms.然而,当采用视觉传感进行状态信息采集时,通常仅相机曝光时间就需要10ms左右,并且由于摆体图像像素点多,计算小车位移和摆杆偏角还需一定的图像处理计算时间,故总的计算时间要远大于10ms,这不但影响控制周期的选择而且极大影响控制系统性能甚至导致控制系统失稳.
2)计算误差.主要来自两方面因素:一方面倒立摆的图像受实验环境例如光照、背景等干扰影响;另一方面工业相机视觉视野必须包含小车和摆杆运动整个区域,离摆体的距离要远大于文献[19]中对应的距离,本文中相机成像平面与倒立摆平面距离约为1m,然而,由于相机较小,倒立摆较大,使得相机平面与倒立摆平面完全平行比较困难,不平行也不可避免地产生误差.然而,由于采样周期短,较小误差就会导致较大的小车速度误差和摆杆角速度误差,进而导致施加在小车上控制力误差大幅度增大,从而使得摆杆偏角和小车位移出现大幅度振荡甚至导致不稳定.例如当小车特征点的像素位移误差为2pixels时,通过计算施加在小车上的对应控制输入误差放大为5.84m/s2.
为了解决以上两个关键问题,接下来首先设计基于事件触发的图像采集策略,然后考虑倒立摆的摆杆与小车特征,进行小车位移和摆杆偏角与图像像素之间的定量关系计算,并分析计算时间与计算误差的统计特性.
2 视觉传感测量
2.1 图像采集
在建立的倒立摆视觉伺服控制实验平台中,相机架设在摆体正前方,并且保持相机所在平面水平及光轴垂直于摆杆自由旋转的垂直面.相机帧率设为100fps,即每帧图像曝光时间为10ms;为了实时连续采集摆体运动图像并降低总计算时间,相机采用事件触发机制进行图像采集,即当一帧图像通过处理计算完小车位移和摆杆偏角后,立即向工业相机发送采集下一帧图像的指令,如图2所示.
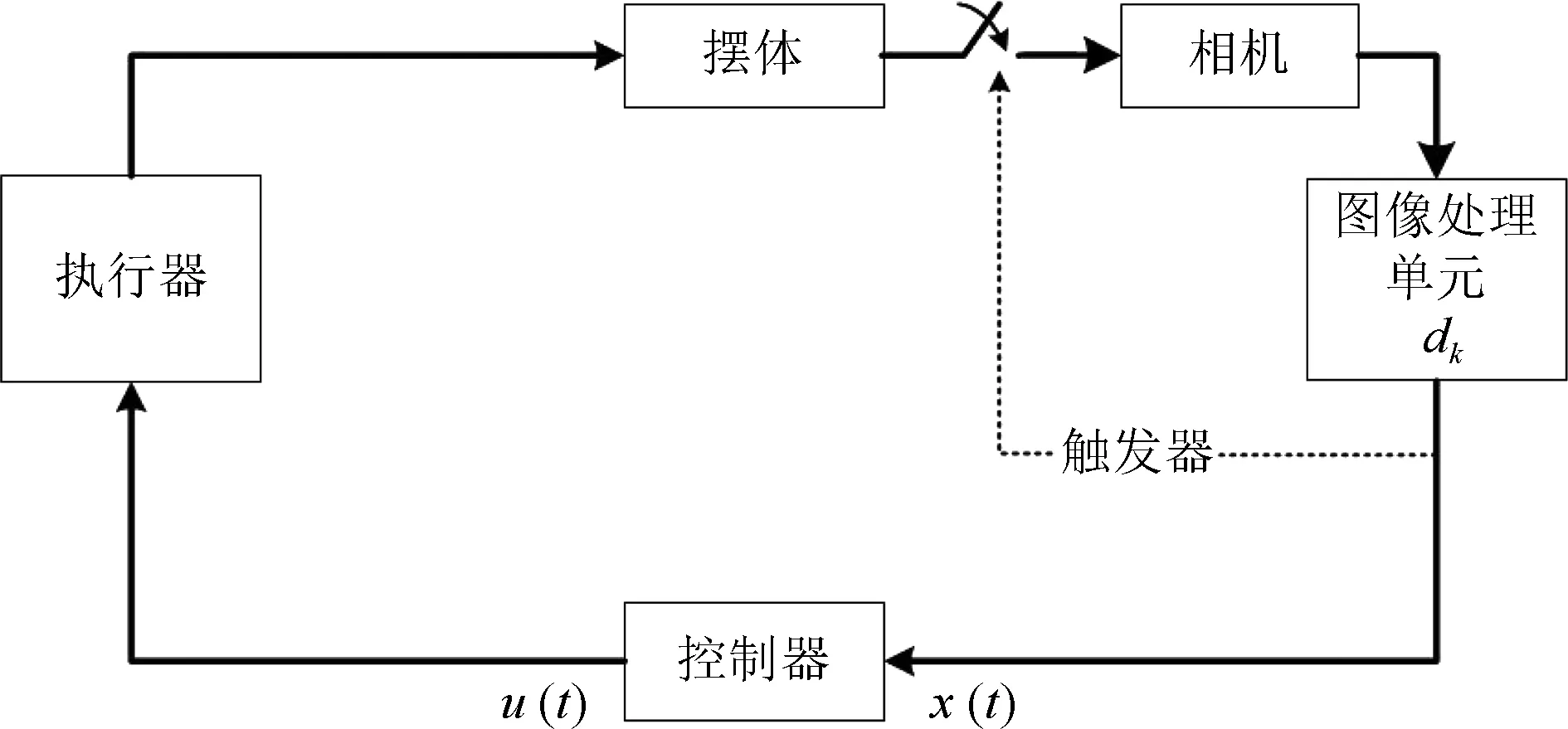
图2 倒立摆视觉伺服控制系统控制框图Fig.2 Control block diagram of inverted pendulum visual servoing control system
注1.在实际实验中设置相机帧率为100fps,图像的曝光时间均设为10ms,能够使图像具有一定的曝光度以保证图像质量,同时曝光时间也不太长,否则会增加总计算时间.工业相机采用事件触发机制,使得相机能够采集尽可能多的图像,从而使控制器能够运用最多的状态信息以提高控制系统性能.然而,由于每次总计算时间的随机性,使得每次采样间隔并不相同,故实际每秒处理图像30∼50帧.
2.2 小车位移和摆杆偏角计算
在工业相机设置好后,不同于传统的光电编码器可以直接获取状态信息,相机采集的摆体图像需要通过图像处理提取出目标特征点信息后,才能快速计算小车位移和摆杆偏角.针对摆体图像,小车位移和摆杆偏角计算过程如图3所示,主要包括图像预处理(S1:局部定位;S2:边缘检测)和状态信息计算(S3:小车位移和摆杆偏角计算).
1)图像预处理.工业相机采集的摆体图像背景为灰白墙体背景,如图4(a)所示,从中可以直观地看到图像信息冗余度较大,为了降低数据量,加快图像处理速度,节省计算时间,需在原图像中分别定位小车和摆杆的运动区域.因为相机和倒立摆之间的距离固定,故运动摆体通过相机透视投影后的图像具有相对固定的分辨率,因此采用行扫描从图像中提取出小车和摆杆的运动区域,如图4(b)和图4(c)所示.然后,采用Canny边缘检测算法[22−23]检测小车和摆杆的边缘信息,如图5(a)和图5(b)所示,在此基础上计算小车位移和摆杆偏角.
2)小车位移计算.摆体图像通过图像预处理(S1,S2)后获得的小车位移以像素为单位,而实际实验平台控制参数是以物理位移为单位,故需要进行单位转换,这通过相机透视投影模型实现[19,22],如图6所示.图6包含4个坐标系,即世界坐标系(Ow:XwYwZw)、相机坐标系(Oc:XcYcZc)、像素坐标系(O0:uv)和成像平面坐标系(O1:xy),其中Oc表示相机光心,Zc表示相机光轴,并且Zc是垂直像素坐标系于主点O1(u0,v0),OcO1表示相机焦距,即f=OcO1,OcOw表示相机光心到摆杆自由旋转垂直面之间距离,即d=OcOw.
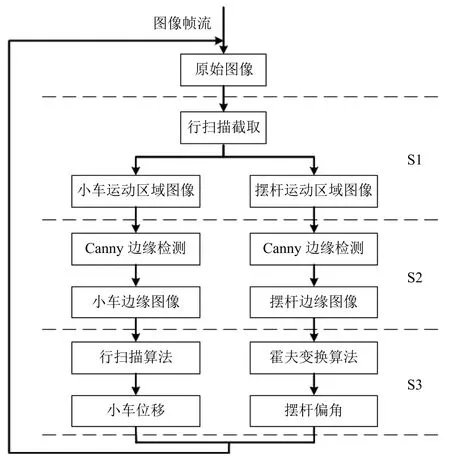
图3 视觉传感测量过程Fig.3 Process of vision sensing measurement

图4 小车和摆杆局部定位Fig.4 Local location of cart and pendulum
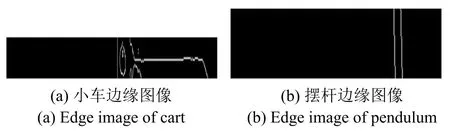
图5 小车和摆杆边缘信息Fig.5 Edge information of cart and pendulum
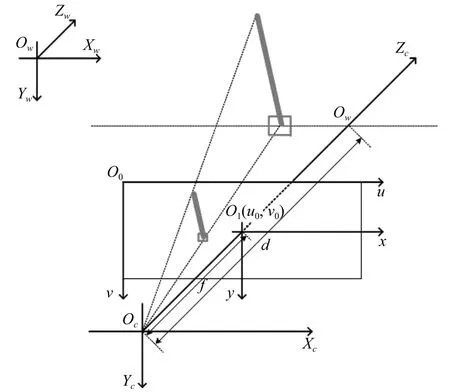
图6 相机透视投影模型Fig.6 The camera perspective projection model
为了得到目标特征点的物理量,世界坐标系和像素坐标系之间的转换关系为
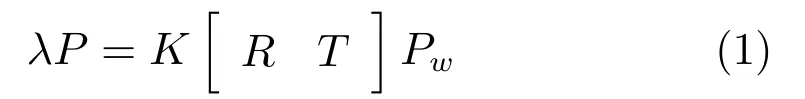
其中,P=[u v1]T和Pw=[XwYwZw1]T分别是目标特征点在像素坐标系中的二维齐次坐标和世界坐标系中的三维齐次坐标,λ是一个标量因子,相机外部参数T∈R3和单位正交矩阵R∈R3×3分别表示像素坐标系和世界坐标系之间的平移量和旋转量.由于倒立摆平台和工业相机均固定不动,故世界坐标系和相机坐标系始终重合一致,则相机外部参数为
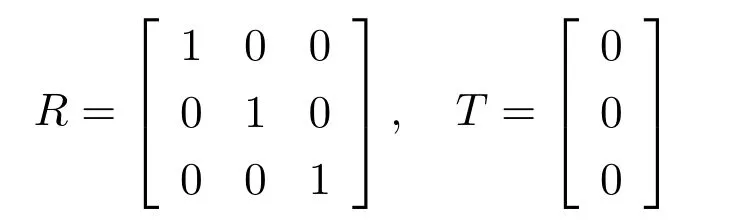
相机内部参数矩阵K∈R3×3采用相机标定[24]确定,即
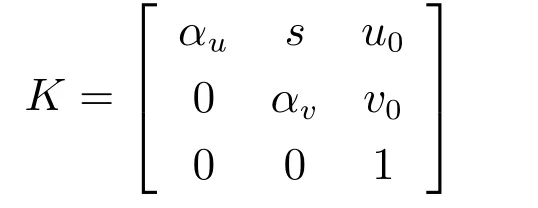
其中,αu=f/dx,αv=f/dy.dx和dy分别为每个像素在成像平面坐标系的x轴和y轴方向上的物理距离.s为因成像平面坐标系的坐标轴不互相正交而导致的倾斜因子,不失一般性,设s=0.
由于世界坐标系和相机坐标系之间没有发生旋转和平移,故标量λ的大小就是目标特征点在世界坐标系中的坐标Zw,也是相机光心到摆杆自由旋转的垂直面之间距离d,即λ=d.通过标定可得相机内部参数,如表1所示.
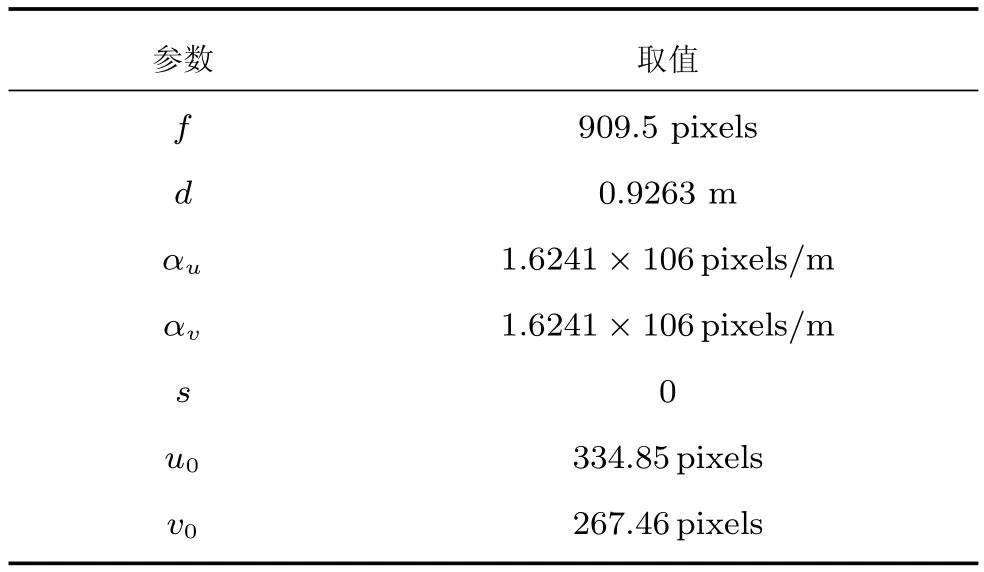
表1 相机内部参数Table 1 Intrinsic parameters of camera
通过式(1)可得
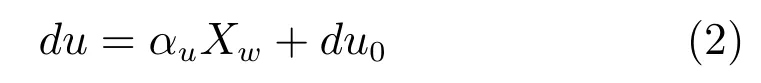
由式(2)可知,在获得目标特征点在像素坐标系中的水平坐标值u后,可计算出目标特征点在世界坐标系中的水平坐标值Xw,即得到小车位移.因此,为了计算小车在像素坐标系中的位移,首先在图5(a)的小车边缘图像中采用行扫描算法[18,21],快速地找出小车的垂直边缘(列坐标),然后根据先验知识定义n个不同的像素行vi(i=1,···,n),如图7所示.接着,采用逐行扫描可得到对应小车边缘的像素列索引ui(i=1,···,n),最后将其平均值作为小车的实际像素位移,即


图7 行扫描检测小车位移Fig.7 Cart position is determined using line scan algorithm
注2.针对以上像素行数n的取值要大于1,使得通过式(3)取均值可降低检测误差,但是n取值也不能过大,否则将大大增加图像处理花费的计算时间而导致实时性差.根据实际实验,本文中取n=3.
3)摆杆偏角计算.由于角度的大小在映射过程中始终保持不变,故摆杆在世界坐标系中的偏角与其在像素坐标系中的偏角相同.二值图像中的直线通常可用霍夫变换(Hough transform)方法[25]检测并计算倾斜弧度.例如对图5(b),采用霍夫变换从摆杆边缘图像中检测摆杆偏角,结果如图8所示.在实际实验中,通常霍夫变换检测出来满足条件的直线不止一条,故计算所有满足条件的直线倾斜弧度,并将平均值作为摆杆偏角.
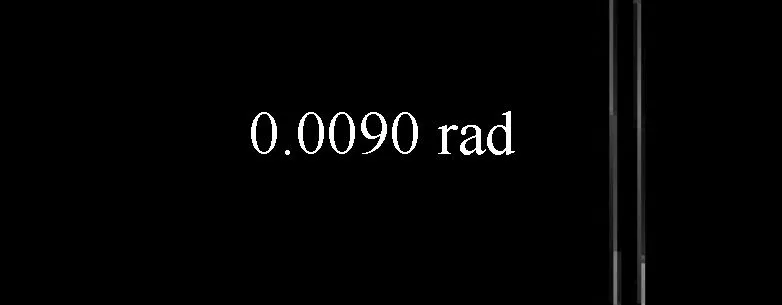
图8 霍夫变换检测摆杆偏角Fig.8 Pendulum angle is determined using Hough transform
2.3 计算时间和计算误差统计分析
1)计算时间统计分析.在图像采集、小车和摆杆图像处理定位及状态信息计算过程中都需要耗费时间,导致小车位移和摆杆偏角状态信息相对相机采样时刻严重滞后.此外,由于光照、背景变化以及摆杆运动变化等因素影响图像质量使得每一帧图像的处理计算时间不尽相同,具有一定的时变性,因此将图像处理计算时间视为定时滞研究具有一定缺陷,需要进一步研究计算时间特性对倒立摆性能的具体影响.为了分析图像处理计算时间的特性,采集了2000帧倒立摆运动图像,然后通过上述图像处理算法计算小车位移和摆杆偏角,同时记录每帧图像处理耗费的计算时间,如图9所示.通过统计分析,发现计算时间变化范围为[0.019,0.029]s.若用,分别表示图像处理计算时间的上下界,则
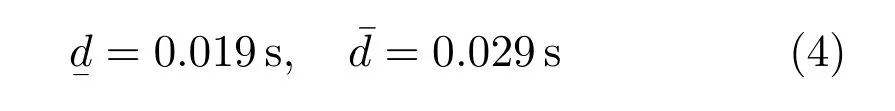
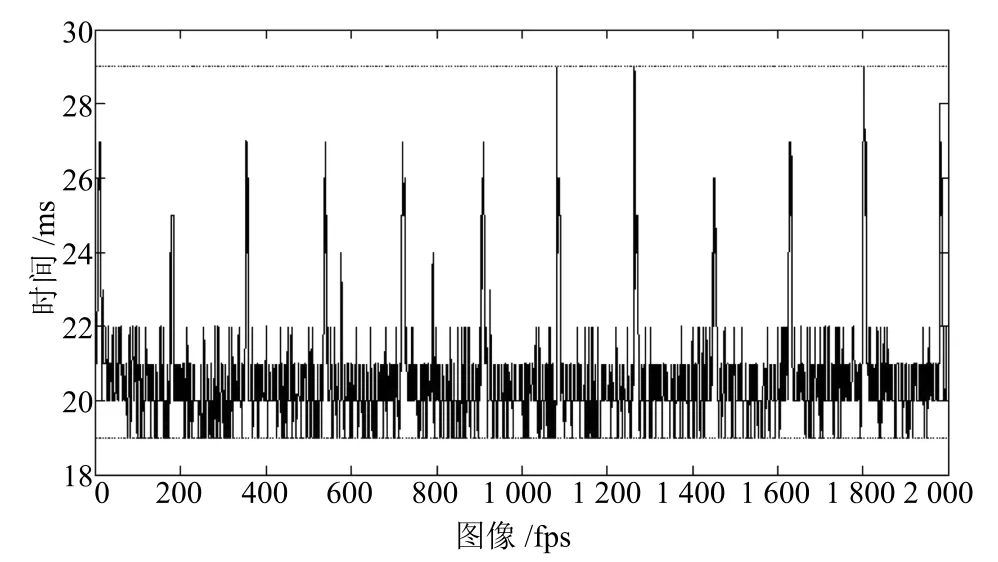
图9 计算时间Fig.9 Computational time
2)计算误差统计分析.在倒立摆实时控制实验过程中,由于背景、光照及实验环境等导致视觉传感采集的图像带有噪声,进而在计算小车位移和摆杆偏角过程中不可避免地产生计算误差.然而,由于影响图像质量难以用精确模型描述,故采用数学统计方法进行误差分析.首先,通过实验采集2000帧倒立摆实时运动图像,同时将每帧图像采集时刻的光电编码器值作为基准值,在此运用同一个定时器,同时启动光电编码器和工业相机以保证工业相机和光电编码器采样时刻一致.接着,对每一帧图像进行处理以计算小车位移和摆杆偏角,将其微分处理后得到小车速度信号和摆杆角速度信号,并与光电编码器采集信息一一对比,小车位移、小车速度、摆杆偏角、摆杆角速度计算误差分别如图10∼13所示.最后,从中可以发现小车位移和速度统计误差分别是 [−0.0015,+0.0015]m,[−0.0015,+0.0015]m/s,摆杆偏角和角速度统计误差分别是 [−0.007,+0.007]rad,[−0.35,+0.35]rad/s.若状态量的图像处理计算误差用err(t)∈R4表示,则
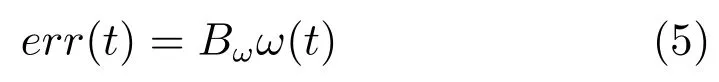
其中,Bω=[0.0015 0.007 0.075 0.35]T,ω(t)∈[−1,+1]是随机变量.
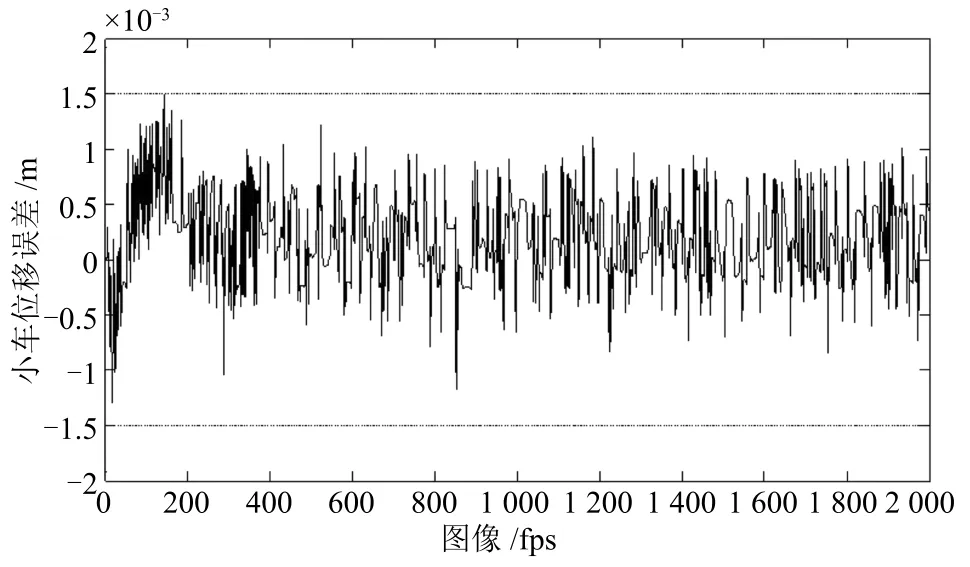
图10 小车位移计算误差统计Fig.10 Computational error statistics of cart position
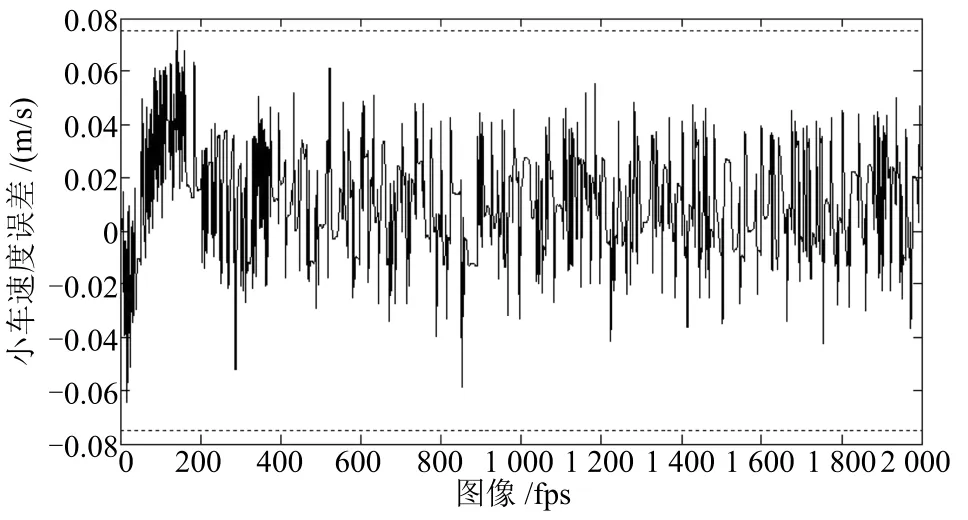
图11 小车速度计算误差统计Fig.11 Computational error statistics of cart velocity
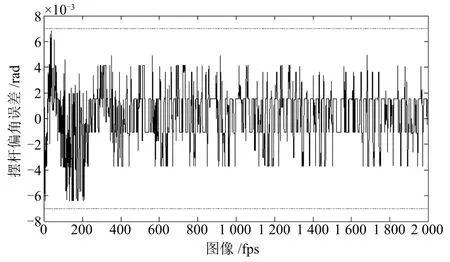
图12 摆杆偏角计算误差统计Fig.12 Computational error statistics of pendulum angle
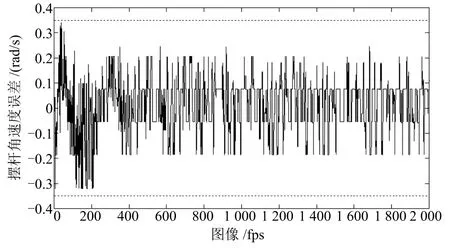
图13 摆杆角速度误差统计Fig.13 Computational error statistics of pendulum angular velocity
注3.统计分析表明,运用视觉传感采集摆体运动图像,然后通过图像处理计算摆杆偏角和小车位移所耗费的计算时间具有时变特性且有上下界.同时,背景、光照及实验环境等带来的图像处理计算误差也是随机且具有上下界,故可将计算误差定义为外部有界干扰.
由于倒立摆稳定控制对实时性和精确度要求非常高,故接下来考虑时变图像处理计算时间和计算误差,建立视觉倒立摆系统模型并进行稳定性分析和控制器设计.
3 系统建模
考虑以上统计的图像处理计算误差(式(5)),根据牛顿运动学定理并在摆杆垂直向上的稳定范围内(|θ|≤0.2rad)进行线性化,可建立倒立摆视觉伺服控制系统状态空间方程,即
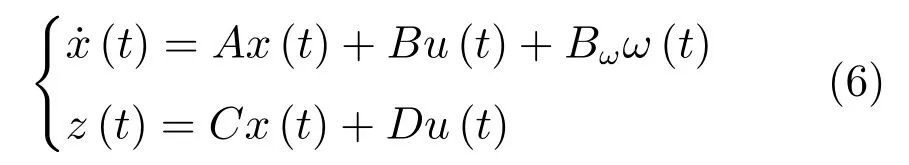
其中,x(t)∈R4是状态量,且x1=α,x3=,x2=θ,x4=分别表示小车位移(m)、小车速度(m/s)、摆杆偏角(rad)、摆杆角速度(rad/s);u(t)表示控制输入信号且为小车加速度;z(t)∈R2表示被调输出;ω(t)∈L2[0,∞)是图像处理计算误差(式(5));A,B,C,D和Bω是已知常数矩阵,具体如下:
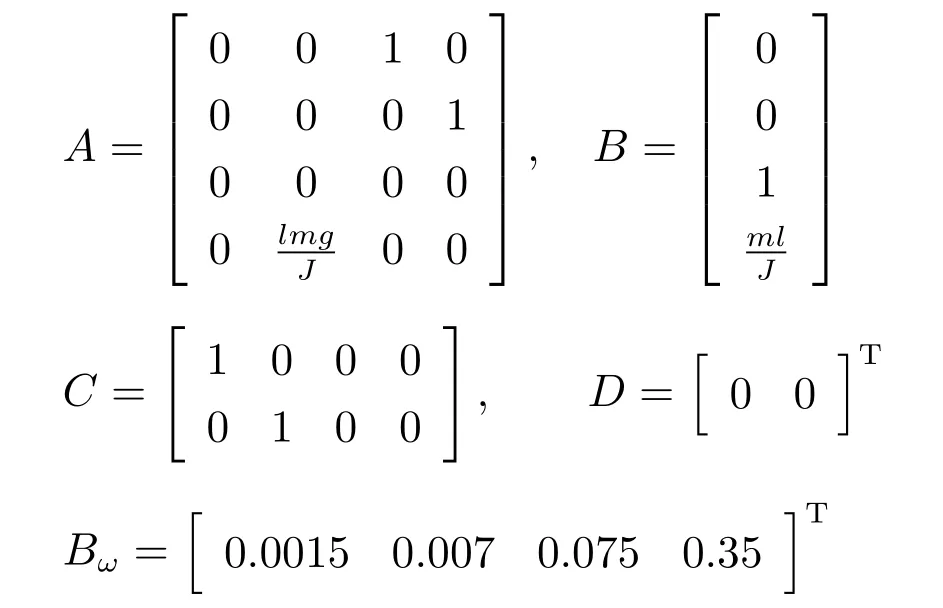
其中,l为摆杆转动点到质心的长度,m为摆杆质量,J为摆杆基于转动点的转动惯量,g为重力加速度,α为小车位移,θ为摆杆与垂直方向的偏转角度.
针对系统模型(6),设计无记忆的全状态反馈控制器

由于相机采用事件触发机制,当每一帧图像通过处理计算完小车位移和摆杆偏角后才进行下一帧图像的采集,如图14所示,tk表示相机采集第k帧图像时刻,dk表示第k帧图像处理花费的计算时间,由式(4)可知其满足
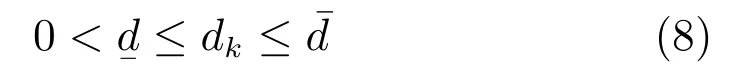
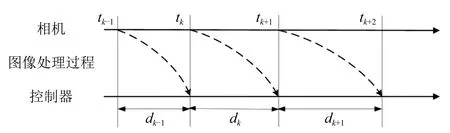
图14 信号时序图Fig.14 Signal timing diagram
从图14可知,控制信号(7)可改写为
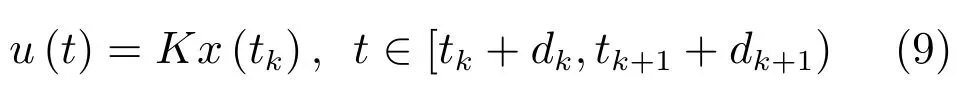
因为相机采集图像时刻tk与计算时间dk密切相关,为了建立tk与dk之间关系,令
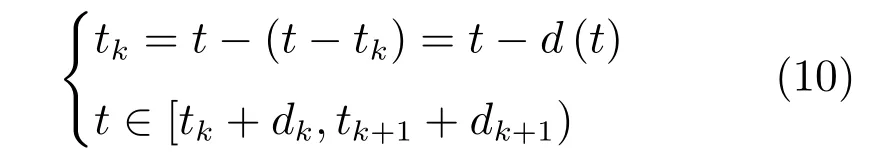
其中,d(t)是具有上下界的时变时延,满足
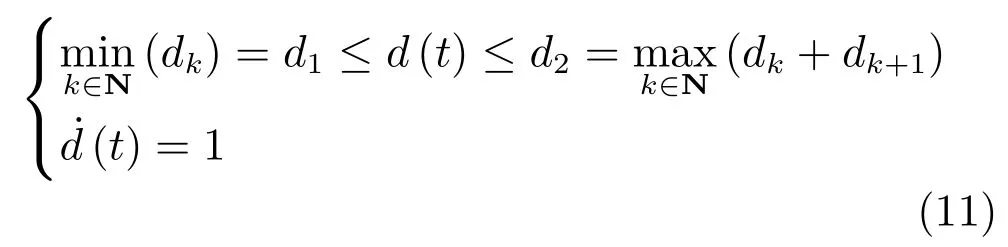
将式(9)和式(10)代入式(6),可得
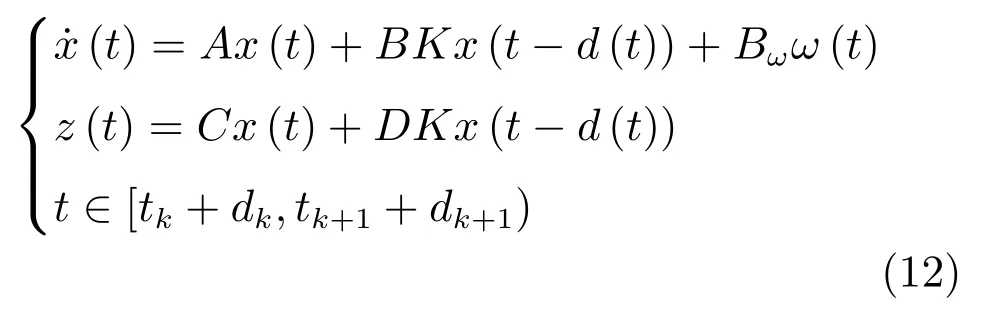
从式(12)可以发现,闭环系统是一个带有时变时延和外部噪声干扰的连续系统,对其稳定性分析可以描述成如下定义的H∞控制问题.
定义 1.H∞控制问题[26−28].对给定常数γ>0,如果系统(12)具有如下性质:
1)系统是渐近稳定的;
2)外部扰动ω(t)到被调输出z(t)的传递函数Gωz(s)的H∞范数不超过给定的常数γ,即在零初始化条件x(t)=0(t∈[−d2,0])下,满足‖z(t)‖≤γ‖ω(t)‖,∀ω(t)∈L2[0,∞),则称系统 (12)具有H∞性能γ,其中‖z(t)‖ ≤γ‖ω(t)‖反映了系统对外部扰动的抑制能力.
若不考虑图像处理计算误差,即ω(t)=0,由以上推理过程可知闭环系统(12)将退化为
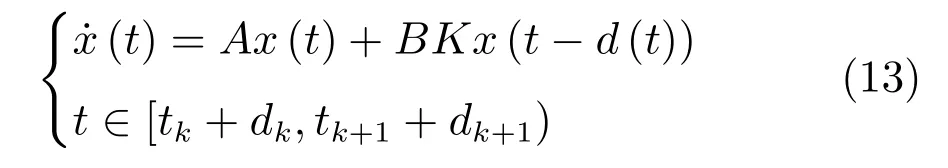
注4.闭环控制系统(12)不仅考虑了时变计算时间特性,而且考虑了计算误差,这不同于目前不考虑计算误差且仅简单考虑计算时间的研究工作[18−21],从而为深入分析计算时间和计算误差与系统性能之间的定量关系奠定了基础.此外,闭环系统(13)仅考虑时变计算时间特性,这也为后续对比分析计算误差对系统性能影响奠定了基础.
4 稳定性分析
首先给出以下三个引理.
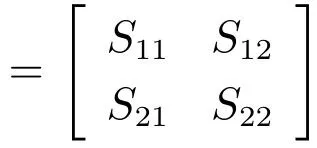
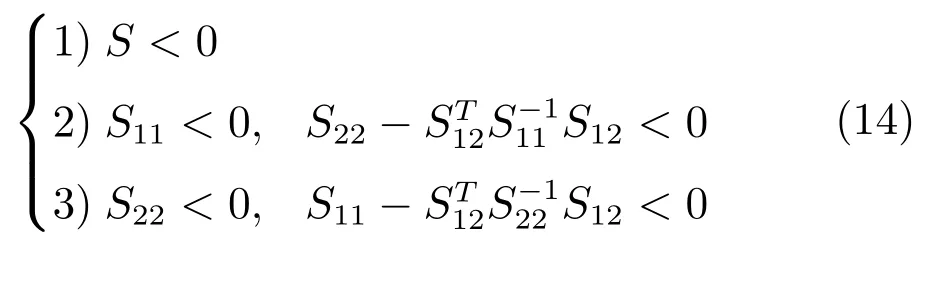
引理2[30].对于给定的实对称矩阵R>0,R∈Rn×n,存在标量γ>0以及向量函数˙x:[−γ,0]→Rn,则以下不等式成立.
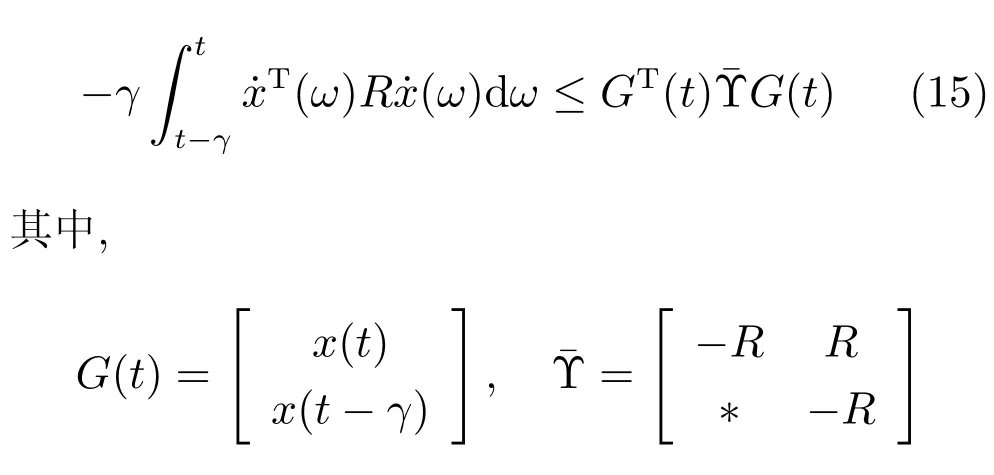
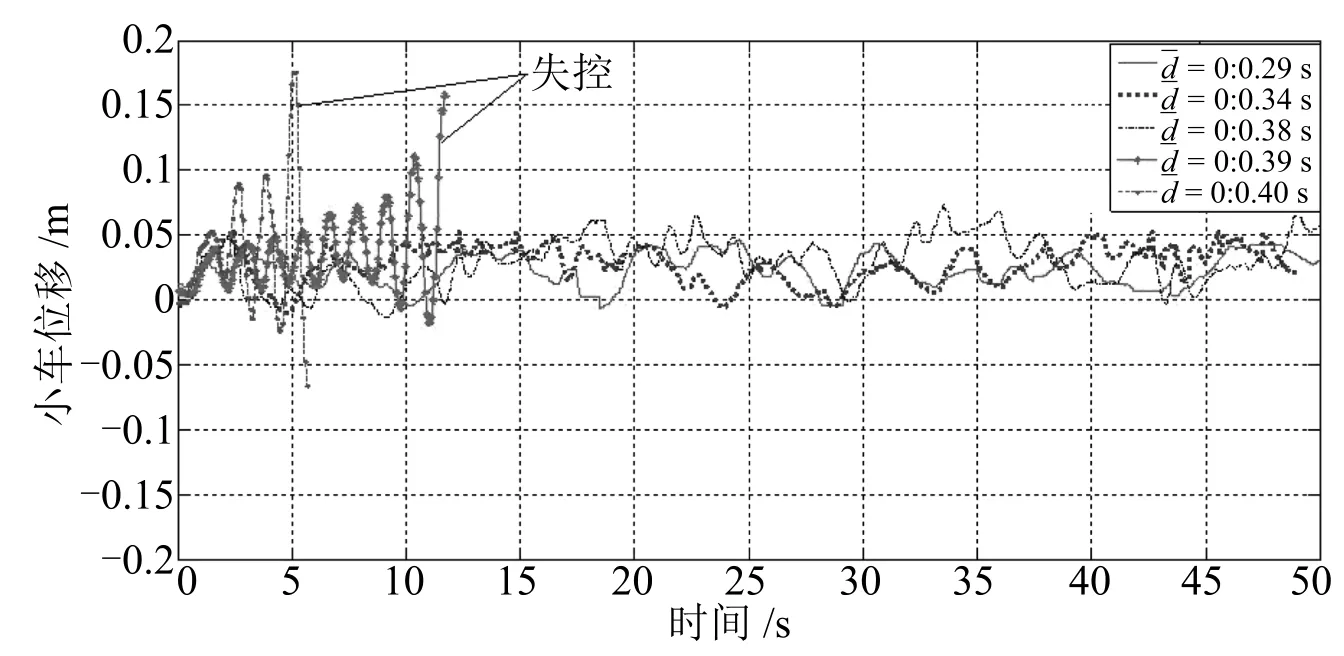
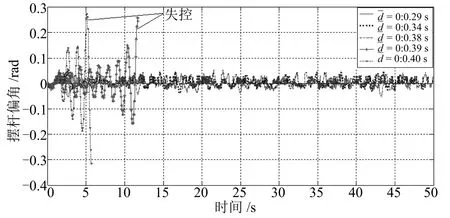
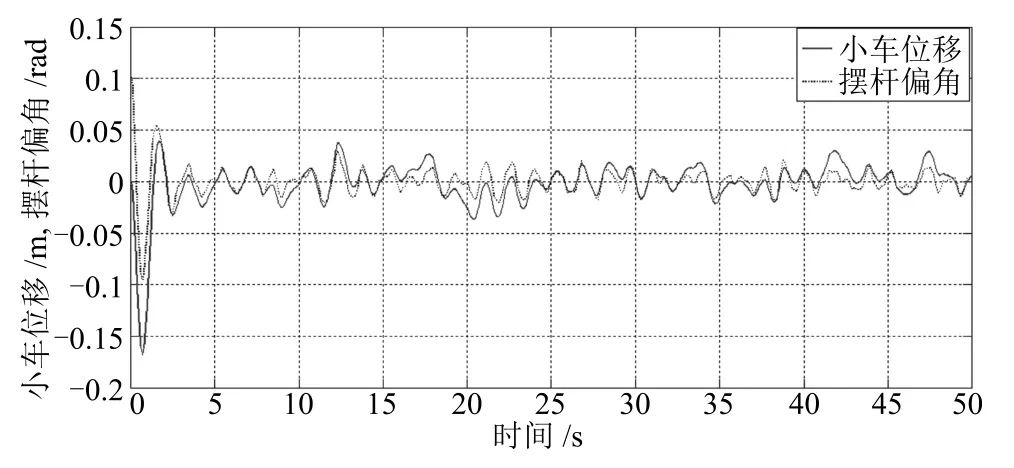
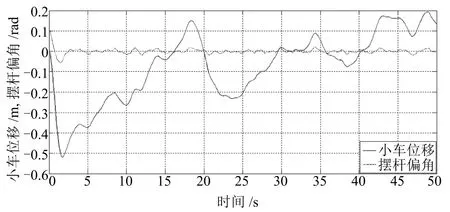
引理3[31].对于给定的实对称矩阵R>0,R∈Rn×n,存在标量0 定理1.对于给定常数0 则闭环系统(12)对所有满足式(11)的时延均渐近稳定,且在零初始条件下具有给定的H∞扰动抑制水平γ. 证明.构造如下Lyapunov泛函: 对V(x(t))关于时间t求导,可得 将式(19)∼(21)相加,可得 应用引理2和引理3,可得 将式(23)∼(25)代入式(22),可得V(x(t))的导数为 接下来从两个方面证明定理1. 1)设ω(t)=0,∀t≥0,则 2)在零初始条件x(t)=0(t∈[−d2,0])下,满足‖z(t)‖≤γ ‖ω(t)‖,∀ω(t)∈L2[0,∞),则 如果Π<0,则 上式两边对t从0∼∞求积分,可得 在零初始条件下,V(x(t))|t=0=0,则 成立,即‖z(t)‖≤γ‖ω(t)‖成立.由引理1可知,矩阵不等式(17)成立,则Π<0成立. 推论1.对于给定常数0 则闭环系统(13)对所有满足式(11)的时延均渐近稳定. 推论1的证明与定理1的证明过程类似,只需将定理1中涉及图像处理误差ω(t)项的行和列(即第5、6行,第5、6列)删除即可,证明略. 注5.定理1证明了受时变时延和计算误差影响的控制系统稳定性,建立了系统稳定性条件与时变时延之间的关系,给出了系统对计算误差的抑制水平.推论1证明了受时变时延影响的控制系统稳定性,建立了系统稳定性条件与时变时延之间的关系. 定理1给出了系统稳定性及H∞扰动抑制水平γ与控制器存在的充分条件,然而通过定理1直接解决反馈增益K困难,因为定理1中存在非线性耦合项如PBK,难以直接运用MATLAB的LMI工具箱求解矩阵不等式获得控制器参数,故需要进行矩阵变换,为此给出定理2. 定理2.对于给定常数0 则闭环系统(12)对所有满足式(11)的时延均是渐近稳定的,并在零初始条件下具有给定的H∞扰动抑制水平γ,且H∞控制器增益为K=Y X−1. 证明.令定理1中的矩阵不等式(17)分别左乘右乘对角矩阵 和它的转置矩阵,并且令 由(εX−R)R−1(εX−R)T>0,其中R>0是实对称矩阵,X是适当维数任意矩阵,可得 推论2.对于给定常数0 则闭环系统(13)对所有满足(11)的时滞均是渐近稳定的,且状态反馈控制器增益为K=Y X−1. 推论2的证明与定理2的证明过程类似,只需将定理2中涉及计算误差ω(t)项的行和列(即第5、6行,第5、6列)删除即可,证明略. 注6.定理2给出了时变时延和H∞性能γ参数下,系统的控制器参数可以通过求解式(33)的可行解得到.推论2在给出了时变时延参数下,通过LMI工具箱求解式(34)的可行解可得控制器参数. 首先,构建倒立摆视觉伺服控制实验平台,如图15所示.根据实际实验平台,可得倒立摆控制系统模型(6)中A和B参数为l=0.25m,m=0.109kg,J=0.009083kg·m2,g=9.81m/s2.根据式(4)可得 图15 实验平台Fig.15 Experimental platform 常量参数γ,ε1,ε2经过多次实验,可设置为γ=2.400,ε1=0.083,ε2=0.104. 然后针对闭环系统(12)和(13),求解定理2和推论2的式(33)和式(34),可得控制增益分别为 下面从两个方面验证所提方法的合理性和有效性. 1)分析图像处理计算误差对倒立摆系统性能的影响 分别从仿真和实际平台实验对控制增益K1和K2进行验证,设置状态初始值均为x0=[0 0.100 0 0]T. 仿真实验:对控制增益K1和K2的仿真结果分别如图16和图17所示.图16是考虑图像处理计算误差设计控制器(控制律K1)的控制效果曲线,图17是不考虑图像处理误差设计控制器(控制律K2)的控制效果曲线.对比图16和图17可以发现,在控制律K1作用下,小车和摆杆均很快进入稳定状态且波动很小,而在控制律K2作用下,虽然摆杆可进入稳定状态,但是小车在轨道上来回大偏移量移动,控制律K1的控制性能明显优于控制律K2的控制性能. 实际平台实验:在图15所示的实验平台上,分别采用控制增益K1和K2进行实时控制实验.实验验证控制增益K1可实现倒立摆稳定控制,其实时控制效果如图18所示,小车和摆杆均在5s内进入稳定状态,其稳定性能比较良好.由于实际实验环境更加复杂多变,多重因素影响倒立摆的实际稳定性能,理论仿真不可能完全模拟实际条件,因此实际的实时控制实验效果跟理论仿真存在一定的差异是合理的.然而,控制增益K2直接无法实现倒立摆的稳定控制. 图16 在控制律K1下的小车位移和摆杆偏角(仿真)Fig.16 Cart position and pendulum angle in controller K1(simulation) 图17 在控制律K2下的小车位移和摆杆偏角(仿真)Fig.17 Cart position and pendulum angle in controller K2(simulation) 图18 在控制律K1下的小车位移和摆杆偏角(实时控制)Fig.18 Cart position and pendulum angle in controller K1(real-time control) 仿真和实际平台实验结果显示,在同等常量参数下,定理2求解的控制律K1的控制性能明显优于推论2求解的控制律K2的控制性能,由此表明对于含有视觉伺服的控制系统研究中,考虑图像处理计算误差对系统性能的影响非常必要. 2)分析图像处理计算时间对倒立摆系统性能的影响 在控制增益K1下,通过仿真实验可得保证闭环系统(12)稳定所允许的时变计算时延最大上界d2=0.089s,即所允许的图像处理计算时间最大上界=0.045s,即当d2>0.089s(即>0.045s)后,系统(12)发散不可控. 为了详细分析图像处理计算时间对倒立摆系统性能的实际影响,在图像处理过程中加上一定的计算时间,使分别达到0.029s,0.034s,0.037s,0.039s,0.040s,进而在控制增益K1下依次进行倒立摆实时控制实验,并设置状态初始初始值均为x0=[0 0 0 0]T.实时控制实验的小车位移和摆杆偏角分别如图19和图20所示.从中可以发现:当=0.029s/0.034s/0.038s时,小车位移和摆杆偏角曲线图没有明显差异,随着增大,小车位移和摆杆偏角曲线图波动略微增大,但没有明显变化,但是当=0.039s/0.040s时,小车位移和摆杆偏角曲线出现剧烈波动并且最终发散,失去稳定. 通过实时控制实验发现,倒立摆能够稳定控制的=0.038s,略小于仿真实验得到的临界值=0.045s,因为实际实验环境比仿真环境更加复杂,理论仿真不可能完全与实际环境一致,故实际实验得到的上界值小于仿真实验得到的上界值是合理的.此外,实验尤其表明,图像处理计算时间对倒立摆系统性能具有非常明显影响,故考虑其时变特性设计控制器更加符合实际. 图19 不同图像处理计算时间上界的小车位移Fig.19Cart position in different upper bound of image processing computational time 图20 不同图像处理计算时间上界的摆杆偏角Fig.20Pendulum angle in different upper bound of image processing computational time 本文主要研究带有时变图像处理计算时间和计算误差的倒立摆视觉伺服实时控制问题.首先研究设计了一种网络化倒立摆视觉伺服控制实验平台,提出了小车位移和摆杆偏角的视觉传感测量实时计算方法,并统计分析了图像处理计算时间和计算误差特性,建立了带有时变计算时间和计算误差的倒立摆视觉控制系统闭环模型,证明了系统稳定性并建立了反映图像处理计算时间与系统稳定性能之间的关系且给出了系统对计算误差的扰动抑制水平γ,并进行了H∞控制器设计.与目前不考虑计算时间和计算误差或将计算时间视为定时滞进行研究倒立摆视觉实时控制方法相比[18−21],本文提出的带时变计算时间和计算误差的倒立摆视觉H∞控制研究更加具有优势.另外,本文研究内容可进一步拓展到双并联倒立摆视觉伺服控制系统,这是后续一项十分有价值的研究工作.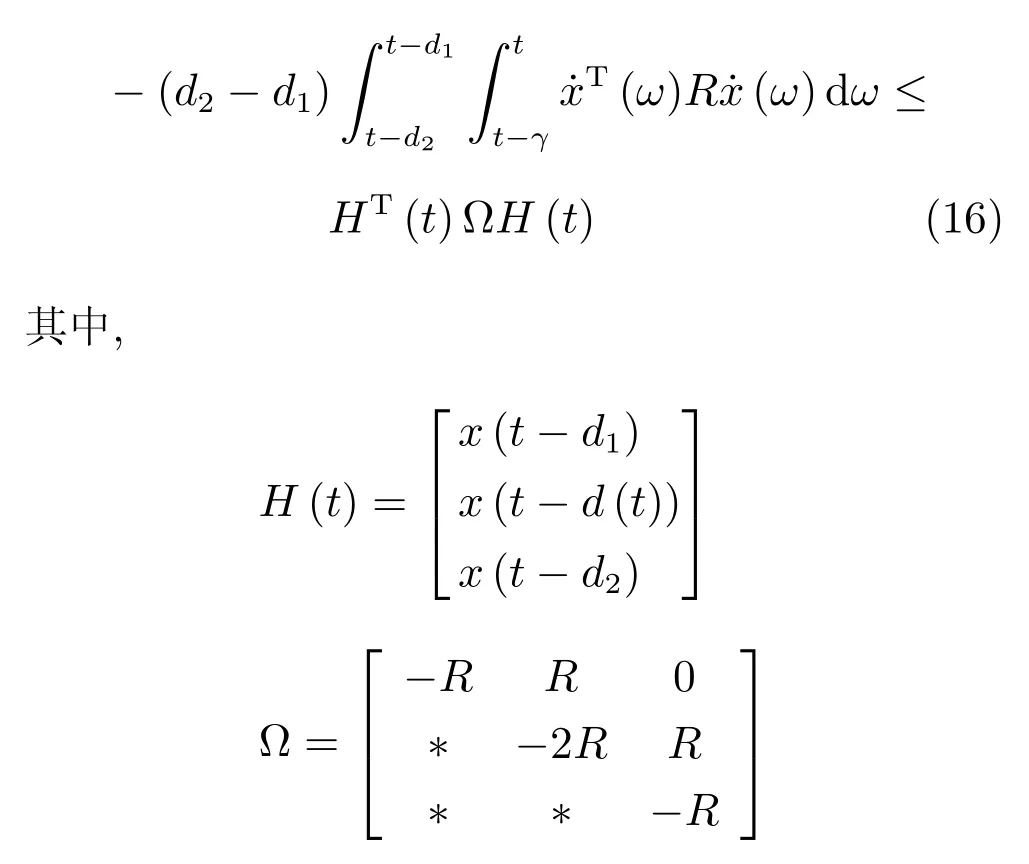

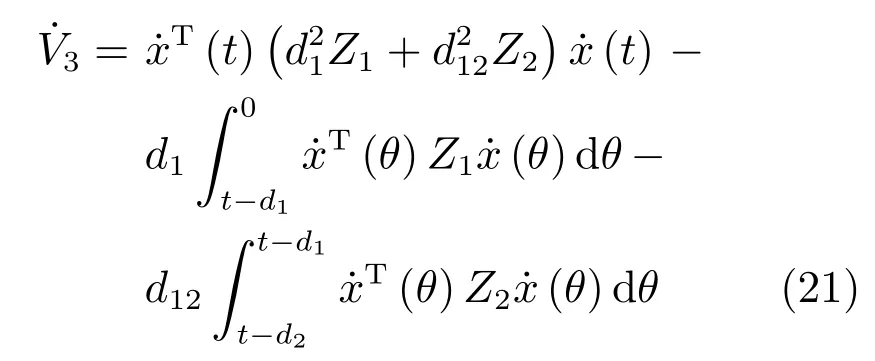
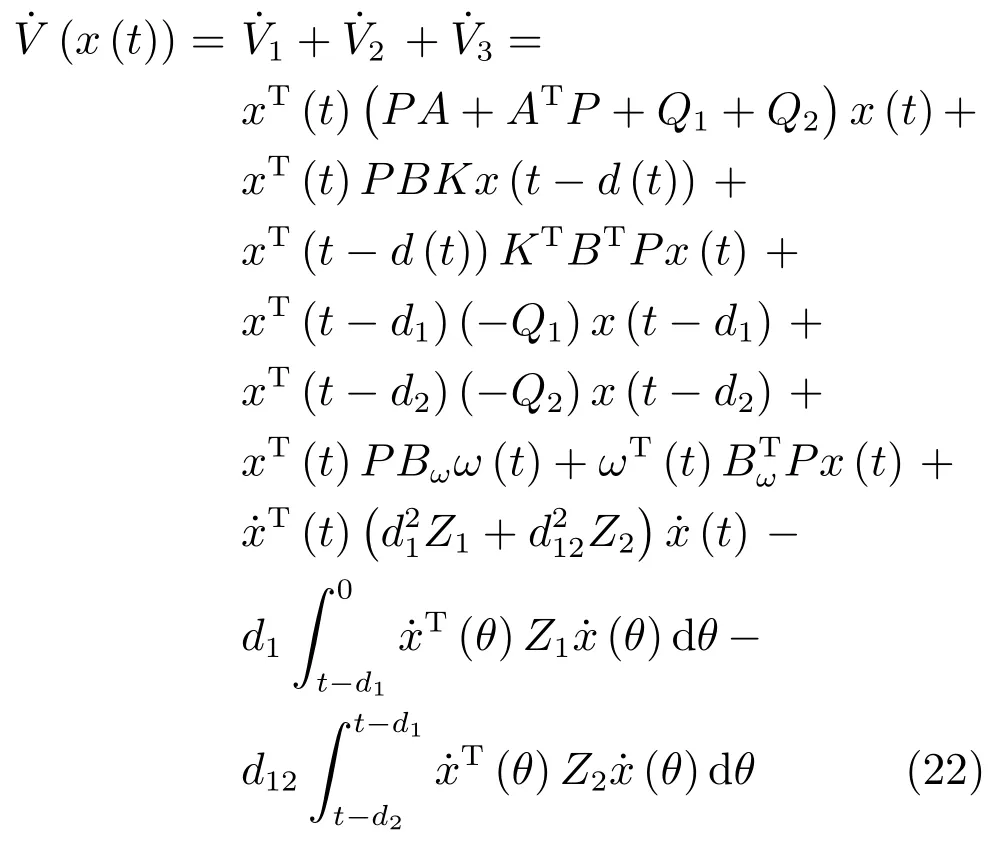

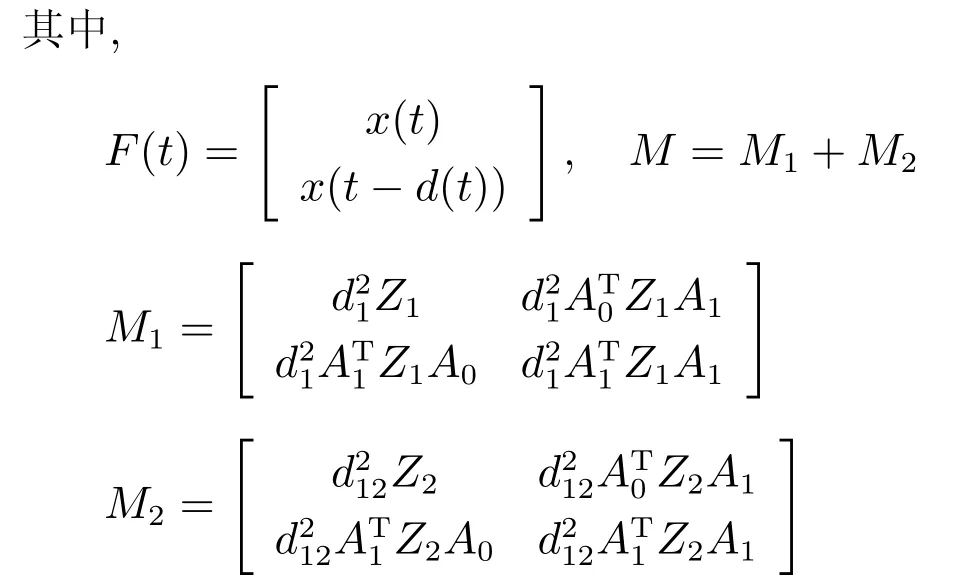

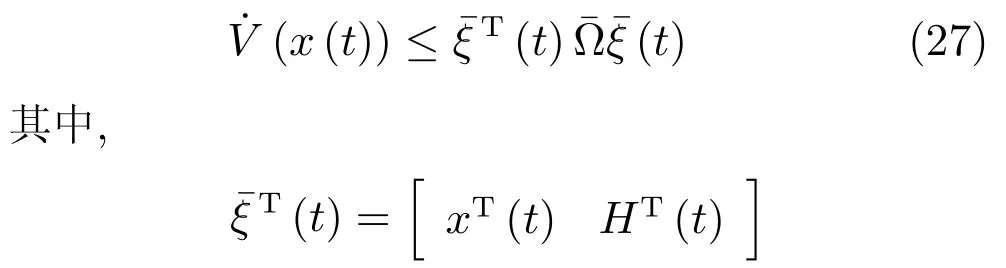
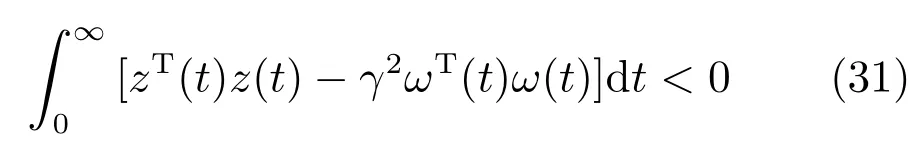
5 控制器设计
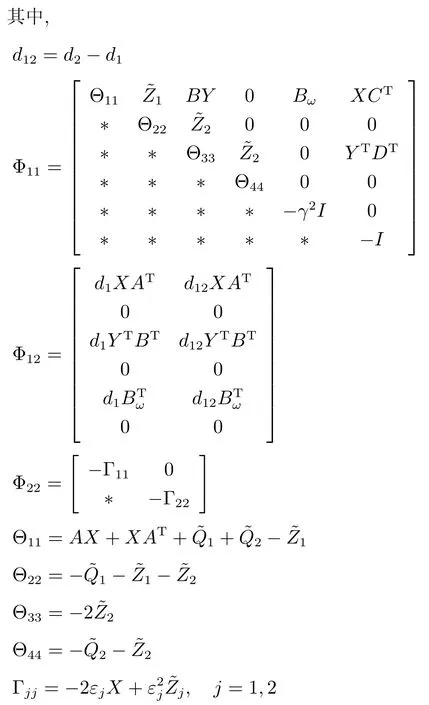
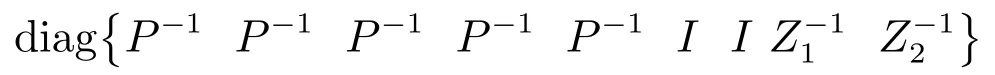
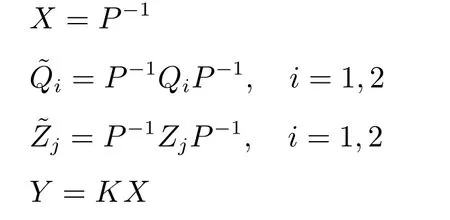
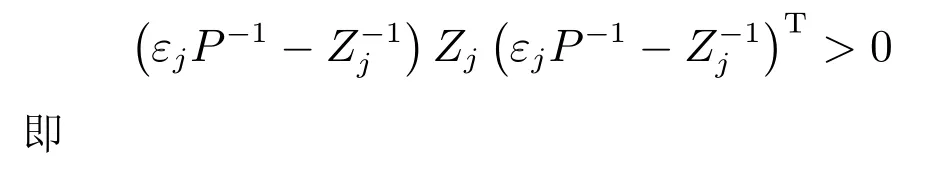
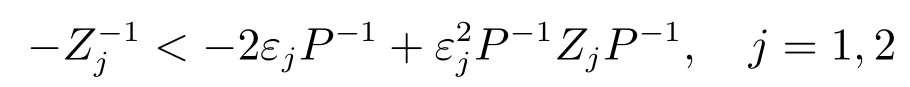

6 仿真和实时控制实验


7 结论