基于改进KAZE的无人机航拍图像拼接算法
2019-04-12韩敏闫阔秦国帅
韩敏 闫阔 秦国帅
随着无人机航拍技术的发展,近年来,其在地图测绘,危险区域安全巡检,地质环境与灾害评估等相关领域得到了广泛应用.无人机航拍图像具有高清晰度,大比例尺的特点.然而,在航拍过程中,无人机由于受到自身飞行高度,相机视角等参数的影响,拍摄的单张图像覆盖面积过小,不能展示更全面的信息.因此,为扩大视野范围,得到覆盖区域更宽广的图像,需要对拍摄的多张航拍图像进行拼接,获得宽视角的全景图[1−3].图像拼接[4]是将相互间有重叠部分的两幅或多幅图像合成一幅大型的无缝高分辨率图像的一种技术.航拍图像的拼接一般包括3个步骤[5]:图像预处理,图像配准,图像融合.其中,图像配准是图像拼接中较为关键的一步,它是图像合成技术的基础[6],其结果会对最后的拼接图像产生重要的影响.
图像配准方法主要分为基于灰度相关的配准,基于变换域的配准和基于特征的图像配准3类[7].其中,基于特征的图像配准方法通过提取图像的局部不变特征对图像的重合部分进行配准,因其算法稳健、快速,已成为研究的热点.常用的特征提取算法包括Harris[8],SUSAN(Smallest univalue segment assimilation nucleus)[9],SIFT(Scale in-varian feature transform)[10−11],SURF(Speed-up robust features)[12−13],ORB(Oriented FAST and rotated BRIEF)[14−15],BRISK(Binary robust invariant scalable keypoints)[16−17],KAZE[18−19]和AKAZE(Accelerated-KAZE)[20]等.其中,Harris和SUSAN算法直接提取角点或边缘特征,不具备较好的环境适应能力.SIFT和SURF通过构造高斯尺度空间得到高斯差分尺度空间,并在其上进行斑点检测,鲁棒性较强,但其不能较好地保留细节与边缘信息.ORB算法结合了一种方向性FAST(Feature from accelerated segment test)与旋转二进制鲁棒独立元素特征BRIEF(Binary robust independent elementary feature),计算速度快,但不具备尺度不变性.BRISK利用AGAST(Adaptive and generic corner detection based on the accelerated segment test)提取角点特征,利用简单的像素灰度值比较构建二进制特征子,具备尺度与旋转不变性,计算速度快,但鲁棒性差.KAZE和AKAZE是基于非线性的特征提取与匹配算法,鲁棒性强,匹配率高.
由于KAZE算法在光照不变性、旋转不变性、尺度不变性、稳定性等方面具有较好的性能,本文针对其算法实时性较差,航拍图像易受光照、旋转变化、尺度变化等影响以及基于K近邻(K-nearest neighbor,KNN)的特征匹配算法耗时较长等问题,提出了一种基于改进KAZE的无人机航拍图像拼接算法.该方法首先利用加速的KAZE算法提取图像的特征点,使用二进制特征描述子FREAK[21]对特征点进行描述,然后采用Grid-KNN算法对特征点进行粗匹配,使用随机一致性算法(Random sample consensus algorithm,RANSAC)算法剔除错误的匹配点对并计算几何变换模型[22],最后采用加权平均算法对图像进行融合.为验证本文算法的有效性,将本文算法与SIFT算法,ORB算法和KAZE算法在Mikolajczyk和Schmid提供的数据集[23]与无人机航拍图像上进行了仿真实验,并在特征点提取速度、特征匹配速度、匹配正确率和配准精度四个方面进行了评价.实验结果表明,本文所提算法是一种稳定、精确度高、拼接效果良好的无人机航拍图像拼接方法.权衡特征点提取速度,特征匹配速度,匹配正确率和配准精度四个方面,本文算法更适合无人机航拍影像的拼接.
1 KAZE算法
KAZE算法是基于非线性尺度空间的特征检测算法.该算法利用非线性扩散滤波器构建具有任意步长的尺度空间,在该尺度空间内,图像的灰度在平缓的区域能够快速扩散,在边缘处以较慢的速度扩散.因此,利用这种非线性方法处理图像时,能够较好的保留细节与边缘信息,同时模糊噪声.
KAZE算法主要包括5个步骤[18]:
步骤1.非线性尺度空间构造.利用可变传导扩散方法和加性算子分裂算法(Additive operator splitting,AOS)构建一个呈金字塔型的非线性尺度空间,如式(1)所示.
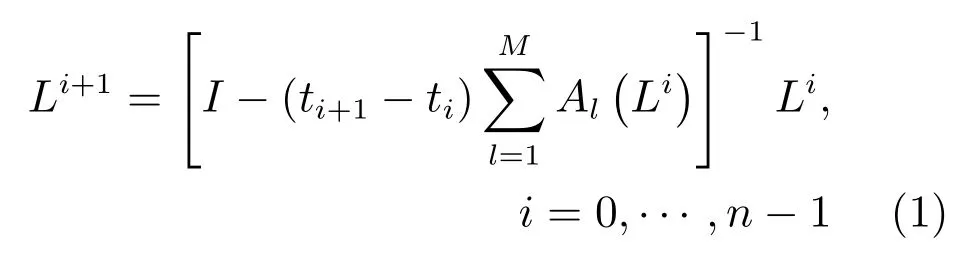
式中,L为高斯滤波后的图像,I为单位矩阵,t为时间,Al(Li)为图像L在维度l上的传导矩阵.
步骤2.特征点检测与精确定位.在不同尺度空间中将每个点与其邻域内的所有点进行比较,寻找归一化后的Hessian矩阵局部极大值点,获得特征点对应的位置和尺度,Hessian矩阵的计算公式如式(2)所示.
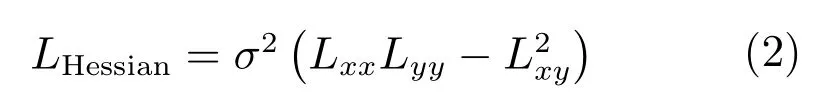
式中,σ为尺度参数σi的整数值;Lxx,Lyy,Lxy均为L的二阶微分.理论上,选择当前及其上下尺度上的大小为σi×σi的3个矩形窗口作为比较范围.但为了提高搜索速度,通常情况下将矩形窗口的尺寸固定为3×3,即将每一个像素点与其同尺度上的8个相邻点,以及上下相邻尺度上的各9个点进行比较.在检测到特征点的位置后,通过子像元插值精确定位特征点.根据泰勒展开式求解亚像素的精确位置.
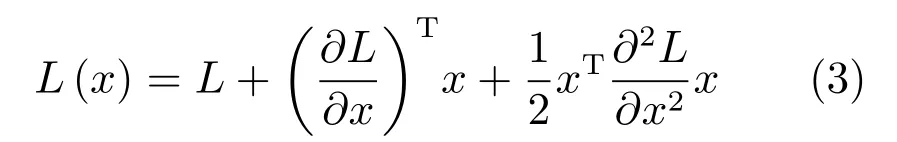
式中x为特征点的位置坐标,特征点的亚像素坐标解为:
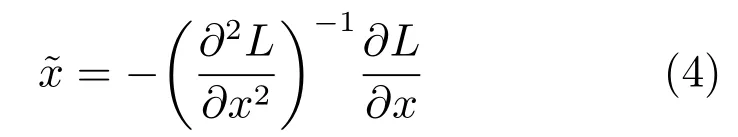
步骤3.特征点主方向确定.特征点的主方向由局部图像结构确定.在搜索半径为6σi的圆内对所有邻点的一阶微分值Lx和Ly高斯加权,然后将所有的微分值作为向量空间中的点集,并在角度为60◦的滑动扇形窗口中叠加点集中的向量,对整个圆形区域进行遍历,以获得最长向量.该向量对应的角度即为主方向.
步骤4.特征向量描述.在特征点的主方向确定后,使用M-SURF算法为每一个特征点构建特征向量.若特征点的尺度参数为σi,则以特征点为中心,在其梯度图像上取一个大小为24σi×24σi的矩形窗口,并将窗口划分为大小为9σi×9σi的4×4个子区域.相邻子区域有交叠,交叠区域的宽度为2σi.使用σ1=2.5σi的高斯核对每一个子区域进行加权,得到长度为4的子区域描述量dv.
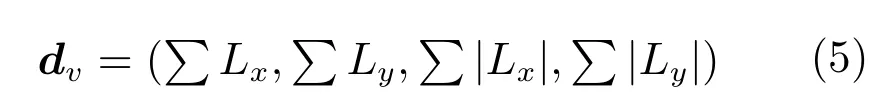
式中,Lx,Ly分别为高斯滤波后的图像L在x,y处的微分.然后,使用尺寸为4×4的σ2=1.5σi的高斯核对每一个子区域的dv进行加权,并进行归一化处理.最终,特征点由一个64维的特征矢量表示.
步骤5.特征向量匹配.使用两特征向量之间的欧氏距离对其进行匹配,欧氏距离越小,两个特征向量越相似,计算公式如下:
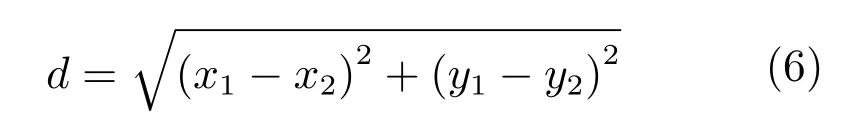
式中,(x1,y1)和(x2,y2)为两特征向量的坐标.
2 改进的KAZE算法
KAZE算法虽然在光照不变性,旋转不变性,尺度不变性及稳定性上具有较好的性能,但实时性较差,难以满足高分辨,大比例尺的航拍图像拼接的速度要求.因此,本文对KAZE算法进行了改进.首先,在非线性尺度空间构建阶段,采用快速显式扩散算法(Fast explicit diffusion,FED)算法代替AOS算法,加速非线性尺度空间图像的生成[20].其次,在特征向量描述阶段使用二进制特征描述子FREAK代替浮点型描述子M-SURF,从而加速特征向量的生成与减少描述子所占内存空间.最后,在特征向量匹配阶段,使用Hamming距离替代原来的欧氏距离,从而减少计算时间提高特征向量的匹配速度.
2.1 非线性尺度空间构造
非线性偏微分方程不存在解析解,因此KAZE算法采用了AOS算法求解方程的近似解.AOS算法在近似求解方程时需要在每个时间步长上大量求解线性方程组才能获得解集,计算消耗时间过多.文献[20]采用了FED算法替代AOS算法近似求解非线性偏微分方程,从而提升算法速度.使用FED算法构造非线性尺度空间不仅能够避免AOS算法计算耗时问题而且能使构造的尺度空间更加准确.因此,本文在非线性尺度空间构造阶段将FED算法内嵌到金字塔架构框架结构中,以加速尺度空间的构造.
2.2 特征向量描述
KAZE算法采用M-SURF算法对特征点进行描述,最终生成一个64维的浮点型特征向量,该向量所占内存较大,且生成时计算复杂,速度较慢.二进制特征描述子根据关键点邻域像素灰度值的比较生成,计算速度快,所占内存空间小.因此,本文采用二进制特征描述子代替浮点型描述子M-SURF,从而加速特征描述子的建立,同时减少对内存空间的需求.常用的二进制描述子主要包括BRIEF算子,ORB算子,BRISK算子和FREAK算子.其中,FREAK算子在光照,旋转及尺度变化的情况下均能保持较好的性能[23].因此,本文选用FREAK算子对KAZE算法提取的特征点进行描述.
FREAK算法是一种模拟人类视网膜结构的快速二进制描述子构建方法.FREAK算法的采样模式如图1所示.其仿照视网膜中神经节细胞的分布模式,位于最中心的为特征点,其他圆心为采样点,离特征点中心越近,采样点越密集,反之越稀疏.在采样时,需要对所有采样点使用大小与当前采样点同心圆半径成正比的高斯核进行高斯平滑.
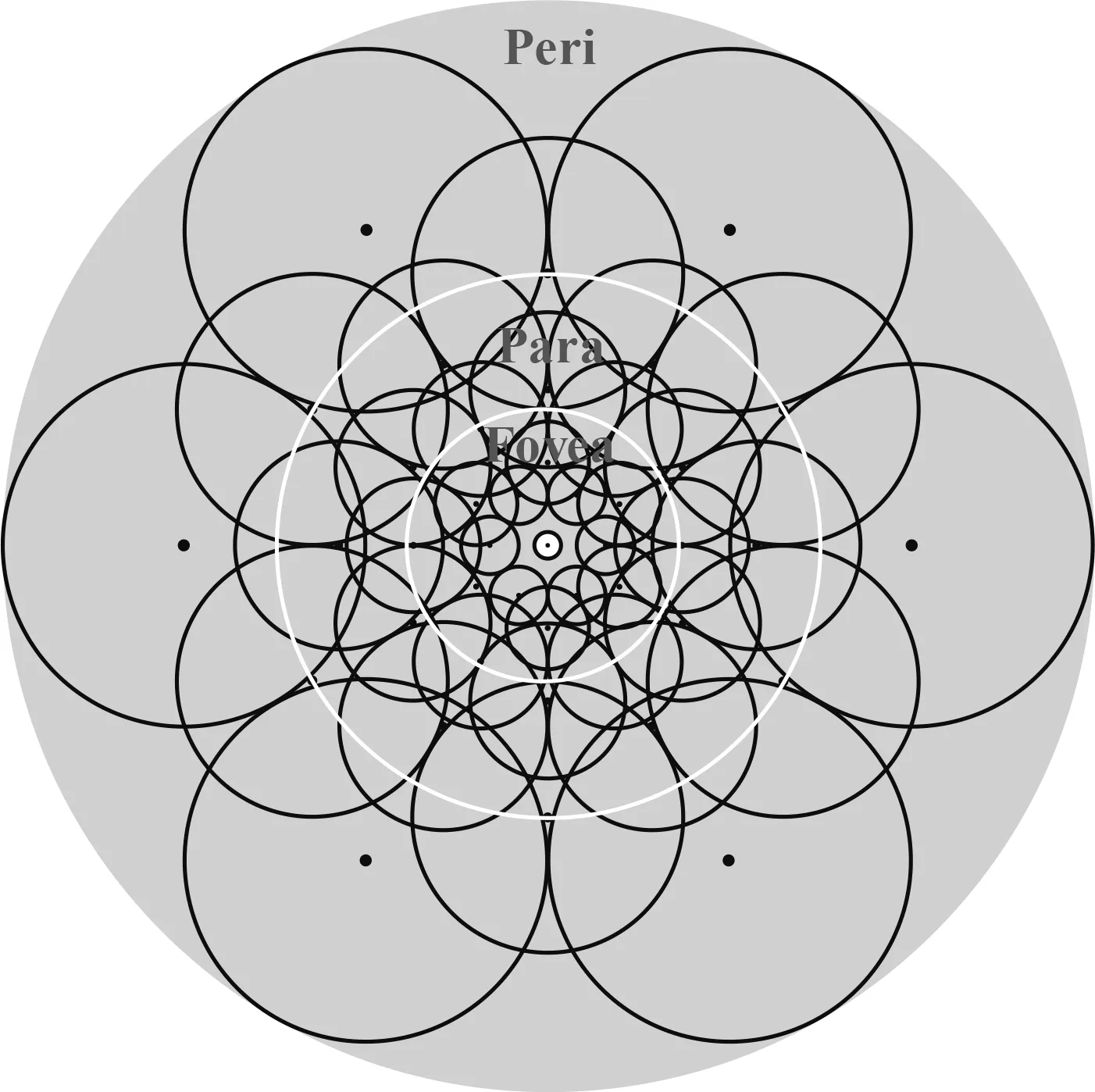
图1 FREAK算法采样模式Fig.1 FREAK algorithm sampling mode
采样后,使用滤波后的图像信息构造FREAK描述子.FREAK描述子最终为一个二进制序列,由采样点对的强度比较结果级联而成,用F表示,则:
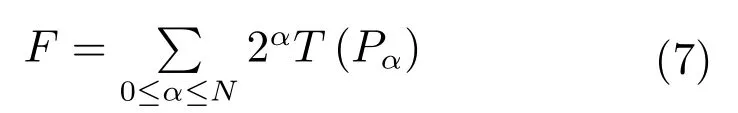
式中,Pα表示感受域对,N为特征向量的维数,T(Pα)的定义如下:
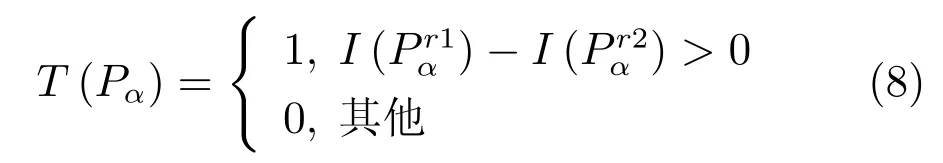
FREAK采样点虽然只有几十个,但其组合而成的采样点对可能达到几千个,信息存在冗余.因此,需要使用类似ORB算子学习算法提取出相关性较小的点对,最终选取前512位作为描述子.为确保描述子具有旋转不变性,在构造描述子时需要确定特征方向.如图2所示,FREAK描述子的特征点周围有43个采样点,可产生903个采样点对,主方向O将由45对中心对称的采样点确定,主方向O的计算公式如下:
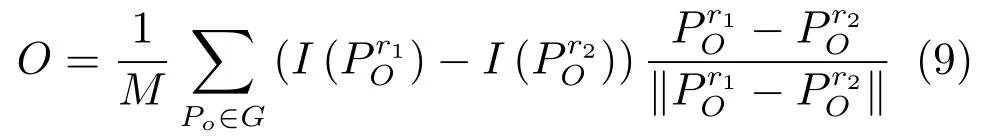
式中,G为确定主方向的特征点对的集合,M是集合G中采样点的对数,是采样点中心的坐标.
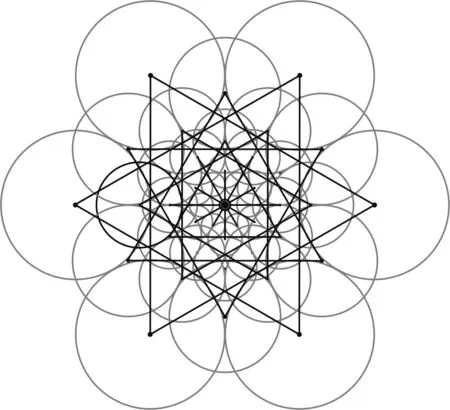
图2 FREAK算法主方向确定Fig.2 Decision orientation of FREAK
2.3 特征向量匹配
由于使用FREAK算子对特征向量进行描述,因此在特征向量匹配阶段使用两个特征向量间的汉明距离对向量进行匹配.使用汉明距离进行特征向量的匹配只需要进行异或操作就可以计算出结果,计算速度快,能够大大提升算法的效率.
3 Grid-KNN算法
在提取特征点,建立特征向量描述后,需要对特征向量进行匹配.基于KNN的匹配算法是一种常用的特征匹配方法.其首先在待配准图像的所有特征点中,依次为每一个参考图像的特征点搜索出与之距离最近的2个点;然后,将最近邻距离与次近邻距离的比值和设定的阈值进行比较.若比值小于设定的阈值,则认为该特征点与其距离最近的待配准图像中的特征点是一组匹配点对.然而,这种方法需要每次都遍历待配准图像中的所有特征点,若参考图像中的特征点数量为N,待配准图像中的特征点数量为M,则总的遍历次数为M×N,耗时较长.因此,在特征匹配时增加运动平滑性约束,以缩小特征匹配区域.正确的匹配在运动空间中是平滑的,运动平稳相邻的特征在运动空间中具有一致性[24].因此,相邻特征点对应的匹配特征点的区域也是相邻的.从而,参考图像中的特征点搜索出待配准图像中与之匹配的特征点后,该特征点邻域内的所有特征点只需在待配准图像中匹配点的邻域内进行搜索即可.匹配区域示意图如图3所示,若参考图像区域a的首个匹配点出现在待配准图像区域b中,则区域a中的余下特征点均在区域b的3×3邻域内寻找匹配点.因此,总的遍历次数将远小于M×N,从而减少匹配时间,加快匹配速度.
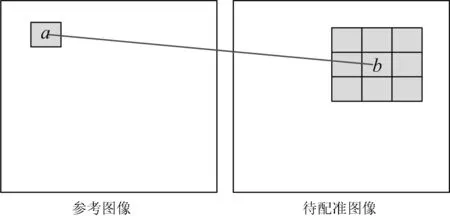
图3 Grid-KNN匹配区域示意图Fig.3 The diagram of Grid-KNN matching area
为方便邻域的选取,在特征点匹配时引入网格框架,将图像均匀划分为n×n的网格,然后以网格为单位,进行特征匹配.基于Grid-KNN特征匹配算法主要包含以下步骤:
步骤1.划分网格.将参考图像与待配准图像均匀划分为n×n个网格;
步骤2.寻找首个正确匹配点对.选取参考图像中的一个网格aij,并在aij中选取特征点Ak.采用基于KNN的搜索方法,找到Ak在待匹配图的所有特征点中的最近邻点Bk和次近邻点Ck,若dAkBk与dAkCk(其中,d表示两点间距离)比值小于设定阈值τ,则认为Ak与Bk是正确的匹配点对,此时结束搜索;否则,选取aij中的下一个特征点,重复上述搜索过程,直到找到首个正确的匹配点对;
步骤3.建立邻域.求取步骤2找到的正确匹配点对中Bk所处网格bij的3×3邻域R;
步骤4.寻找所有正确匹配点对.依次选取网格aij内剩余的特征点,按照步骤2的搜索过程,找到网格aij和区域R中所有剩余的正确匹配点对;
步骤5.对步骤1中参考图像的剩余网格,重复步骤2∼4,直至所有网格遍历完毕.
4 无人机航拍图像拼接
无人机航拍图像在特征匹配后,需要计算几何变换参数进行变换,并对配准后的图像做融合处理.本文在使用加速KAZE算法提取航拍图像特征点,并采用FREAK对提取的特征点进行描述后,使用Grid-KNN算法对特征点搜索,进行粗匹配,特征点匹配程度采用汉明距离进行衡量.影像区域特征具有相似性,经常会导致相邻特征点的误匹配,通过Grid-KNN算法对特征点进行匹配后,往往会存在错误的匹配点对.因此,使用RANSAC算法剔除误匹配点对,对匹配结果进一步提纯.在获得精匹配的特征点对后,使用RANSAC算法求解几何变换矩阵,将待配准图像经变换矩阵变换后与参考图像进行叠加.由于图像之间存在亮度与色彩差异,需要对叠加后的图像进行融合,以消除拼接缝.使用加权平均融合算法对叠加的图像进行融合,计算公式如下:
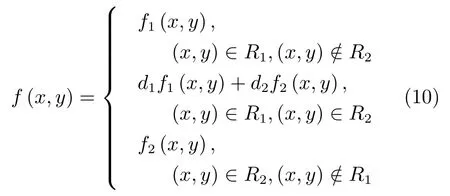
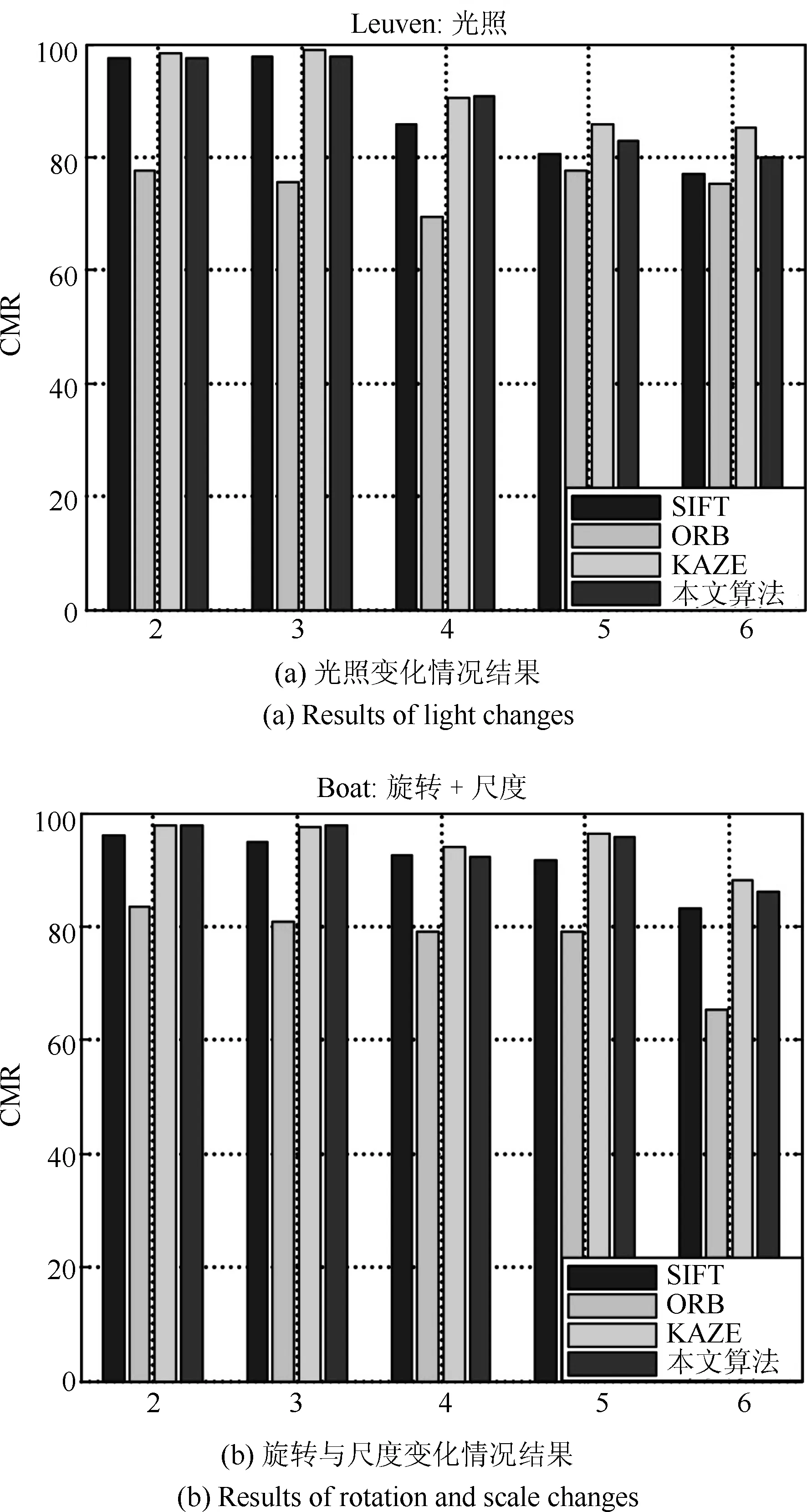
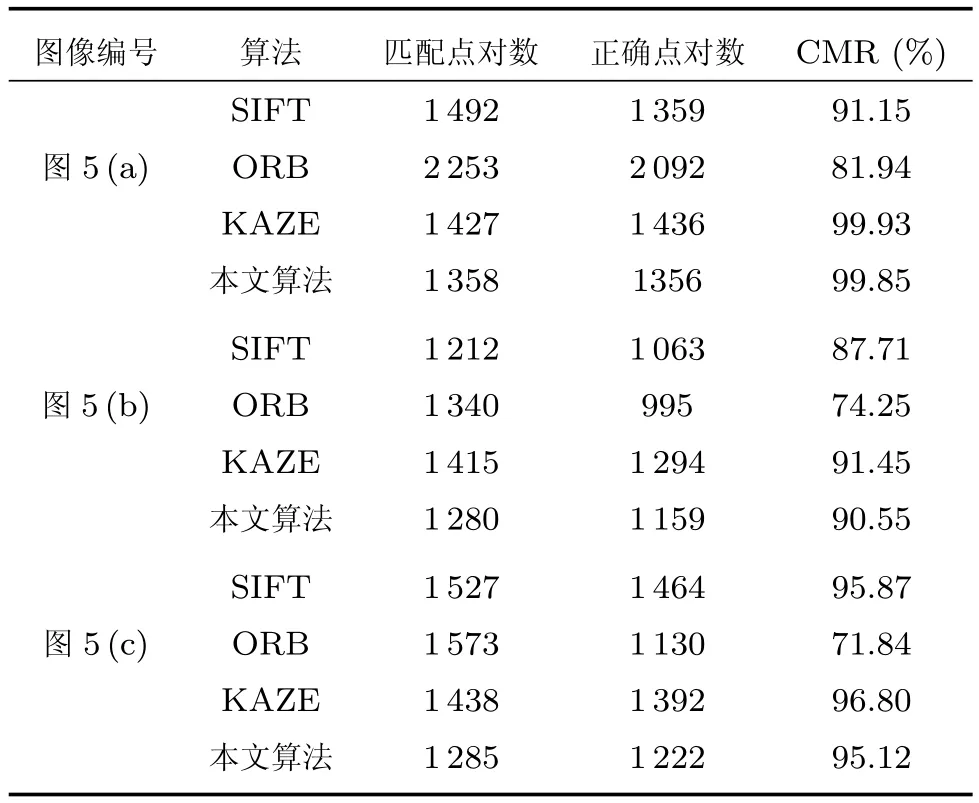
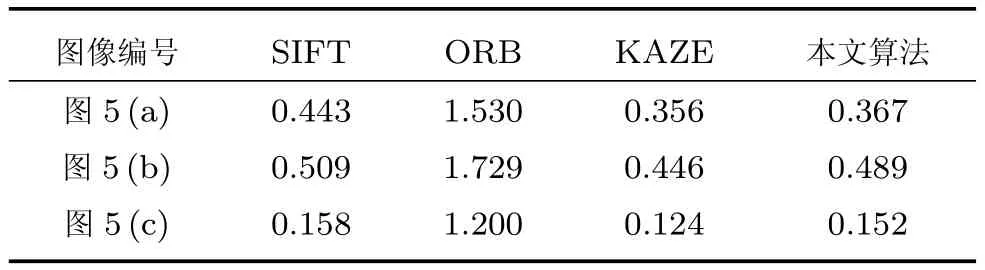
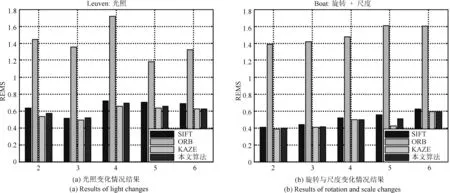
式中,R1为图像1的区域,R2为图像2的区域,d1,d2为加权值,且d1+d2=1,0 步骤1.特征点检测.使用加速的KAZE算法检测出航拍图像的特征点; 步骤2.特征点描述.采用二进制特征描述子FREAK对检测出的特征点进行描述; 步骤3.特征点粗匹配.采用Grid-KNN算法搜索出参考图像与待配准图像特征点中的正确匹配点对; 步骤4.特征点精匹配.使用RANSAC算法对匹配的特征点对进一步提纯,将可信度较低的匹配对进行过滤,得到精匹配结果; 步骤5.建立几何变换模型.选取单应性矩阵作为相邻两幅图像间的变换模型,使用RANSAC算法求解其变换参数; 步骤6.图像融合.使用加权平均融合算法对配准后的图像进行融合,使重叠区域的像素按照相应的权重进行叠加,以消除拼接图像的拼接缝,使图像色彩,亮度过度更加自然,真实. 图4 基于改进KAZE算法无人机航拍图像拼接流程Fig.4 The process of UAV aerial image mosaic based on improved KAZE algorithm 在图像拼接中,衡量一种算法是否适合无人机航拍图像的重要指标包括特征点提取与匹配速度,匹配正确率和配准精度.因此,针对本文提出的基于改进KAZE的无人机航拍图像拼接算法,采用了标准数据集和大量无人机航拍图像进行实验,并将本文算法与SIFT算法,ORB算法和KAZE算法进行比较,从特征点提取速度,特征匹配速度,匹配正确率和配准精度四个方面对各算法进行定量的评价与分析.实验运行环境采用CPU为Intel core i3,3.50GHz,内存为4GB,64位Win10操作系统的PC机.本文实验的所有算法基于OpenCV2.4.10实现,编程语言为C++语言,编程环境为Visual Studio 2010.实验数据采用Mikolajczyk和Schmid提供的数据集中的Leuven数据,Boat数据和图5中所示的无人机航拍图像.Mikolajczyk和Schmid提供的数据集包含了具有不同几何和光照强度变换的几个图像集,每个图像集包含了6个图像序列,每个序列的后5张图像是对第1张图像的变换.Leuven数据和Boat数据分别用于验证图像在光照变化,旋转变化和尺度变化下的算法性能;图5所示的各组航拍图像的分辨率均为4000×3000,分别对应光照变化,旋转变化和尺度变化的情形. 图5 实验数据Fig.5 Experimental data 表1 特征点提取平均用时比较(ms)Table 1 The comparison of feature point extraction average time(ms) 特征点提取速度评价采用提取每个特征点的平均用时进行比较,平均用时越短,速度越快.表1给出了分别使用SIFT算法,ORB算法,KAZE算法和本文所提算法对Leuven数据,Boat数据和图5所示的实验数据进行特征点提取的平均用时比较.从表中可以看出ORB算法特征点提取时间最少,本文算法次之,SIFT算法和KAZE算法特征点提取时间最长.这是因为ORB算法采用FAST方法检测特征点,且在特征描述时只需对特征点的邻域进行二值测试,因此特征提取速度性能较好.SIFT算法构造高斯尺度空间进行特征点检测,KAZE算法构造非线性尺度空间进行特征点检测,且二者均采用浮点型描述子进行特征描述,因此二者较为耗时.本文算法,虽然需要构造非线性尺度空间进行特征点检测,但是采用二进制描述子描述特征,因此速度与SIFT算法和KAZE算法相比得到了大幅提升. 特征匹配速度评价采用每个特征点的平均匹配用时进行比较,平均用时越短,速度越快.表2给出了分别使用SIFT算法,ORB算法,KAZE算法和本文所提算法对Leuven数据,Boat数据的前2个图像序列和图5所示的实验数据进行特征匹配时平均用时比较.其中,SIFT算法,ORB算法,KAZE算法均采用基于KNN的特征匹配算法,本文算法的网格大小选为10×10.从表中可以看出SIFT算法和KAZE算法耗时最长,ORB算法次之,本文算法耗时最短.SITF算法和KAZE算法使用欧氏距离进行特征相似性度量,且使用基于KNN的特征匹配算法,因此,耗时较长.ORB算法虽然与本文算法一样采用汉明距离进行特征相似性度量,但其采用的基于KNN的特征匹配算法相较于本文的Grid-KNN算法遍历次数较多,耗时较长. 表2 特征匹配平均用时比较(ms)Table 2 The comparison of feature matching average time(ms) 匹配正确率CMR(Correct matching rate)为匹配正确点对数与所有匹配点对数之比,其定义如下: 式中,N为所有匹配点对数,Nc为匹配正确点对数.CMR是一种客观的评价指标,其值越大,匹配性能越好.图6给出了使用4种算法对Leuven数据和Boat数据进行匹配的匹配正确率结果.从图中可以看出KAZE算法和本文算法在光照,旋转和尺度变化下具有较好的性能,SIFT算法次之,ORB算法最差.因此,本文算法抗光照变化,抗旋转和抗尺度变化性能更好,稳定性更强.表3给出了使用4种算法对图5所示航拍图像进行匹配的匹配正确率的结果比较.从表中的结果可以看出ORB算法的匹配正确率最低,SIFT算法次之,KAZE算法和本文算法最好,进一步验证了本文算法在光照,旋转和尺度变化下具有较好的性能与稳定性. 图6 Leuven数据和Boat数据匹配正确率比较Fig.6 The comparison of correct matching rate for Leuven data and Boat data 配准精度直接影响着最终的拼接结果,其采用参考图像与待配准图像之间的距离均方根误差RMSE(Root mean square error)进行评价,RMSE的计算公式如下: 式中,M为监测点总数,(xi,yi)为参考图像中监测点的坐标,为待配准图像中经单应性矩阵变换后的监测点的坐标.RMSE的值越小,两者间的距离越小,则配准精度越高,拼接效果越好,反之,拼接效果越差. 表3 匹配正确率比较Table 3 The comparison of correct matching rate 图7给出了使用4种算法对Leuven数据和Boat数据进行配准后的均方根误差结果.从图中可以看出KAZE算法和本文算法在光照,旋转和尺度变化下均方根误差最小,具有较好的配准精度,SIFT算法略次之,ORB算法最差. 表4给出了使用4种算法对图5所示航拍图像配准后的均方根误差的结果比较.从表中的结果可以看出ORB算法的误差最大,配准精度最差,SIFT算法较好,KAZE算法和本文算法拥有最好的配准精度.本文算法的配准精度虽略低于KAZE算法,但略高于SIFT算法,同时远高于ORB算法,说明本文算法在光照,旋转和尺度变化的情况下具有较好的配准精度,能够适用于无人机航拍图像拼接.图8给出了使用本文算法对图5中的3组实验数据进行配准后的结果.从图中可以看出配准后的图像无明显的错位,配准效果较好. 由上述实验结果可知,ORB算法虽具有较快的特征点提取速度,但其在追求特征点提取速度时大大牺牲了匹配正确率与配准精度;SIFT算法和KAZE算法的匹配正确率与配准精度较高,但其特征点提取速度与特征匹配速度过慢;本文算法在保持较高的匹配正确率与配准精度的同时保持了一定的特征点提取速度,并且特征匹配速度较快.综上所述,均衡特征点提取速度、特征匹配速度、匹配正确率与配准精度四个方面,本文算法更具优越性. 表4 配准精度比较Table 4 The comparison of matching accuracy 图7 Leuven数据和Boat数据匹配精度比较Fig.7 The comparison of matching accuracy for Leuven data and Boat data 图8 图像配准结果Fig.8 The results of matching 使用本文算法对图5中的三组图像进行配准,在使用加权平均算法对配准后的图像进行融合,最终的拼接结果如图9所示.从图中可以看出,拼接后的图像无鬼影、无拼接缝,且图像亮度变化均匀,保真度高,拼接效果较好. 针对航拍图像易受光照、旋转变化、尺度变化等影响,KAZE算法实时性较差以及基于K近邻的特征匹配算法耗时较长等问题,本文提出了一种基于改进KAZE的无人机航拍图像拼接算法,并与SIFT算法,ORB算法和KAZE算法进行了对比.该方法首先利用加速的KAZE算法提取图像的特征点,采用二进制特征描述子FREAK进行特征点描述,然后使用Grid-KNN算法对特征点进行初步匹配,采用RANSAC算法对匹配的特征点对精匹配并计算几何变换模型,最后使用加权平均算法对图像进行融合.实验结果表明,本文算法在特征匹配速度,匹配正确率和匹配精度上拥有较好的性能的同时保持了一定的特征点提取速度.与KAZE算法和SIFT算法相比,本文算法在保持匹配正确率和配准精度的同时提升了特征点提取速度与匹配速度;与ORB算法相比,本文算法虽然在特征点提取速度上有所减慢,但是较大提高了特征匹配速度、匹配正确率和配准精度.综合特征点提取速度、特征匹配速度、匹配正确率与配准精度四个方面,本文算法较上述算法更适合无人机航拍影像的拼接. 图9 图像拼接结果Fig.9 The results of stitching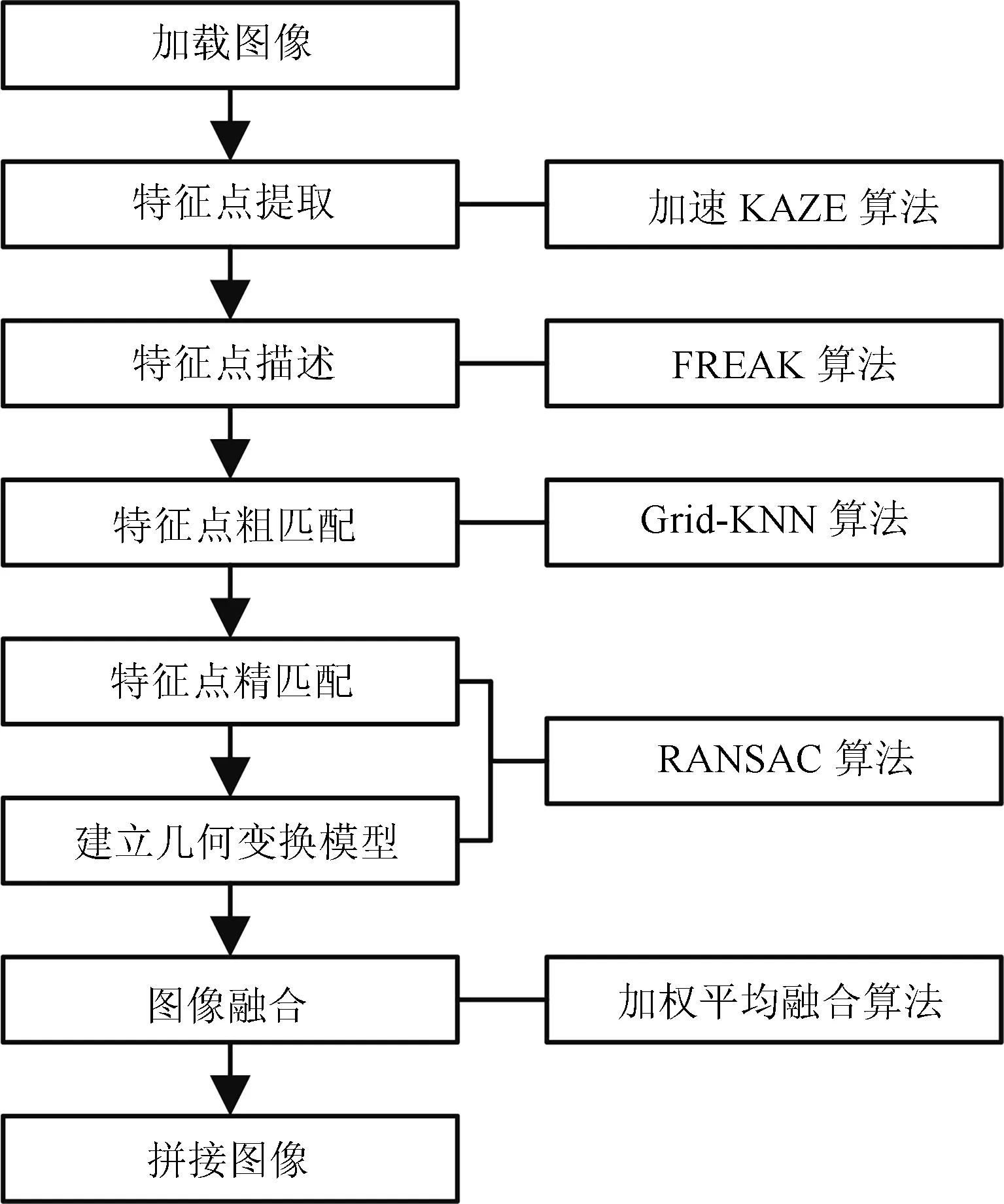
5 实验结果及分析
5.1 特征点提取速度对比

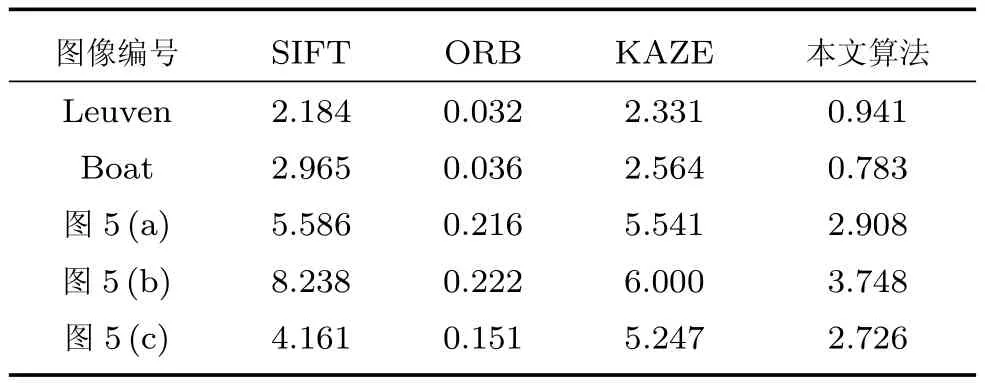
5.2 特征匹配速度对比
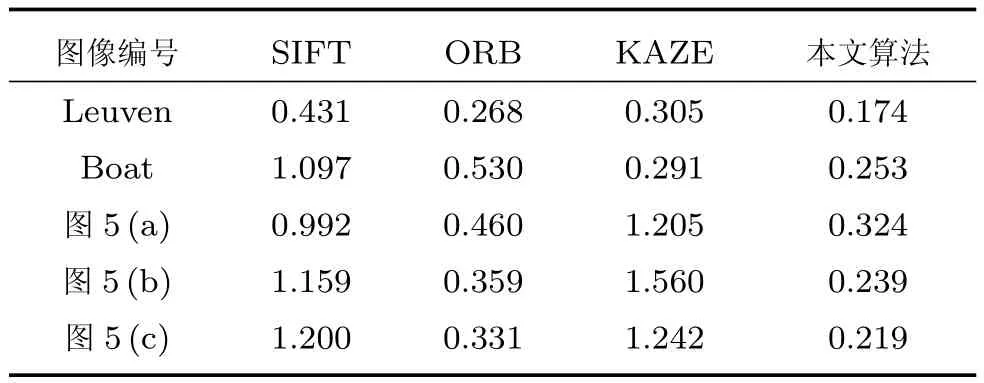
5.3 匹配正确率对比

5.4 配准精度对比
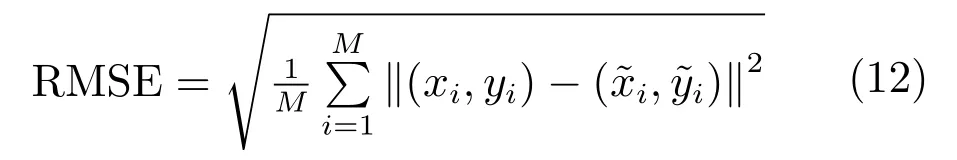

5.5 图像拼接结果
6 结论

