基于模糊层次分析的灰色关联法在地下水水质评价中的应用

吕子明，丁坚平，褚学伟，张雪梅，令狐燕艳

(贵州大学 资源与环境工程学院，贵州 贵阳 550025)

地下水作为水资源的一部分既是人类赖以生存的物质资源，又是重要的环境要素。地下水资源独特的赋存环境及其水力交替条件，决定了地下水自净能力差、自身难污染，一旦污染却又难治理的特点。目前，由于城镇化、工业化的不断推进，更多的污染物进入地下水中，影响了区域性的生态环境平衡，而且使满足人类饮用的水量越来越少。因此，为了更好地管理保护和开发利用地下水资源，防治和控制地下水污染，进行合理科学的地下水水质评价尤为重要。

地下水水质评价是地下水资源评价的一项重要内容，它的主要任务是根据地下水的主要物质成分和给定的水质标准，分析地下水水质的时空分布状况，为地下水资源的开发利用规划和管理提供科学依据[1]。目前，有关地下水资源水质评价的方法众多，其中一般常见的有：单因子评价法、综合评价法、层次分析法、模糊综合评价法、灰色系统法、人工神经网络法等。这些方法各具特色，但也有各自的适用范围和局限性。如单因子评价法分别对单个指标进行分析评价，不能全面地反映地下水质量的整体状况[2]；综合指数法易将污染物的污染指数放大，使得评价结果等级偏高，不能很好地反映水质污染的真实状况；层次分析法需考虑判断矩阵一致性问题，在判断矩阵的构造中，也未考虑人为判断的模糊性[3]；模糊综合评价法体现了水环境中客观存在的模糊性和不确定性，但可能存在水质类别判断不准确的问题；灰色评价法在评价因子满足“曲线相似”的情况下评价精度才较高[4]；人工神经网络的建立必须以大量样本为基础，且计算复杂，收敛速度慢[5]。因此，在充分把握各个方法适用性及局限性的基础之上，通过将多个独立的方法进行适当的结合，在规避各方法局限性的前提下，充分发挥各方法应有的优点，使评价结果更加科学合理。目前，在地下水水质评价领域这样的方法较多，但多是两种方法的结合，其评价结果虽较单个方法的使用更加科学，仍存在不足之处。

鉴于以上分析，本文采用基于模糊层次分析的灰色关联方法进行地下水水质评价。使用模糊层次分析法确定地下水水质评价因子的相对权重，在此基础上利用灰色关联分析方法进行量化分析，确定地下水水质评价因子的综合关联度，最大关联度即地下水水质等级[6]。

1 确定评价因子权重

以往计算评价因子权重多采用层次分析法。其关键在于构造判断矩阵，各因子权重一般由判断矩阵特征向量确定，但在进行计算权重之前需要判断判断矩阵的一致性，若不一致还需重新构建，使得层次分析法的计算过程显得较为繁琐[7]。

本文利用模糊层次分析法计算评价因子权重。根据模糊数学的研究成果，将层次分析法和模糊集相结合，得到模糊层次分析法。其相对层次分析法的优点在于其判断矩阵的模糊性，这种判断矩阵可以通过一定的方式转化为模糊一致性矩阵，减少了对判断矩阵的一致性检验，使得权重的计算过程变得简洁。

1.1 建立模糊互补判断矩阵

模糊判断矩阵是指建立在一定模糊标度基础上的判断矩阵。判断矩阵是指各个评价因子根据选取的模糊标度值进行两两比较而得出的相应判断值所构成的矩阵，记为A=(aij)n×n。若判断矩阵中的任一元素均在[0，1]范围内，此矩阵为模糊判断矩阵。若模糊判断矩阵中的任意元素存在aii=0.5，且aij+aji=1(i，j=1，2，…，n)，则这个矩阵称为模糊互补判断矩阵。

模糊标度的选取通常采用0.1～0.9标度法给予数量标度。对于评价因子ai与aj，其判断值aij具体的判断标度见表1。本次研究中模糊互补判断矩阵采用两个(或多个)领域专家打分的方法进行建立。

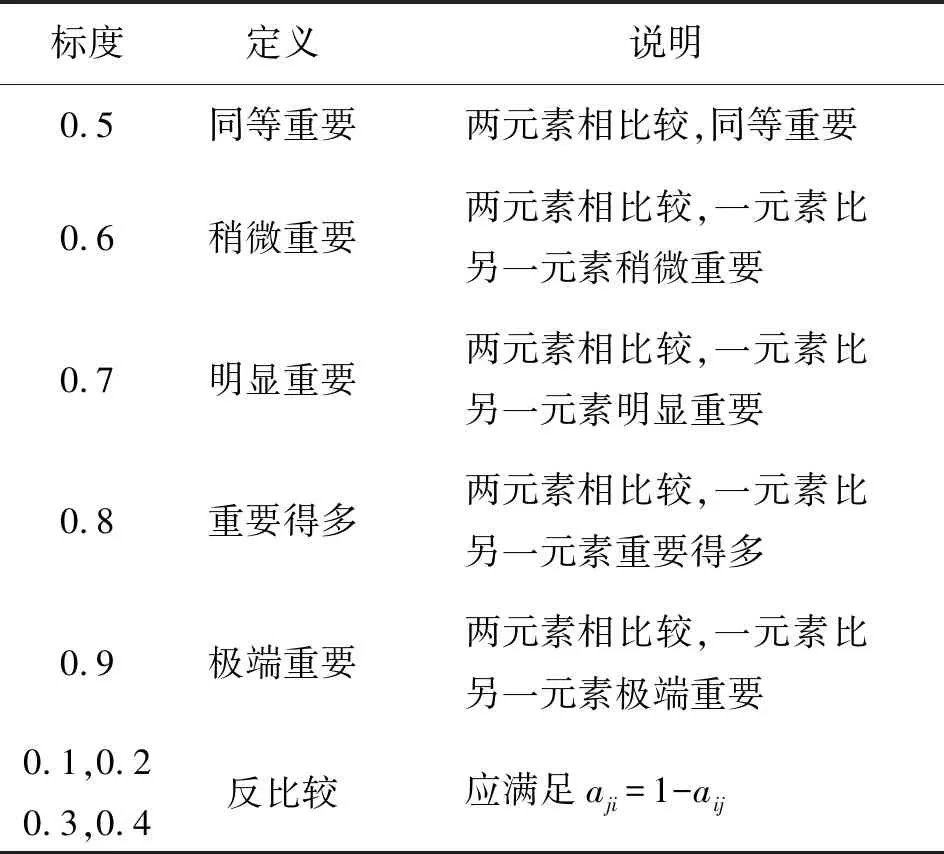
表1 模糊型0.1～0.9标度含义

1.2 建立模糊一致性矩阵

模糊一致性矩阵可以由已经得出的模糊互补矩阵经一定的变换得到。当模糊互补判断矩阵A=(aij)n×n中元素满足aij=aik-ajk+0.5(i，j，k=1，2，…，n)，则这个矩阵具有加性一致性。若其元素满足aikakjaji=akiajkaij(i，j，k=1，2，…，n)，则这个矩阵具有乘性一致性。本文使用的0.1～0.9标度属于加性标度，因此可以通过加性一致性矩阵的定义对模糊互补矩阵进行一定的转换，得到模糊一致性矩阵。对模糊判断矩阵A进行转化，得到模糊一致性矩阵，记为R=(rij)n×n。转换公式如下：

(1)

式中：ri，rj分别为模糊判断矩阵A中第i，j行中各元素的和，m为评价因子的个数。

1.3 模糊一致性矩阵权重的确定

目前计算权重有多种方法，一般应用较多的是最小二乘法。对上述已得到的模糊一致性判断矩阵，可由最小二乘法分别得到m个评价因子ai对应的权重为：

(2)

2 建立基于模糊层次分析的灰色关联地下水水质评价方法

灰色关联分析是灰色系统理论的一种分析方法，灰色系统理论以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定系统为研究对象[8]。地下水水质分级或水体是否污染并非非黑即白，具有不确定性，其中的不确定性具有灰色性，因此可采用灰色关联法进行水质评价。

本文将灰色关联分析法和模糊层次分析法进行结合，建立地下水水质评价方法。其结合可行性分析如下：(1)模糊层次分析法采用专家打分的方法，为偏于主观性的评判方法；灰色关联法进行量化计算，为客观性的评判方法。充分考虑评价方法的主观性和客观性，使其评价结果更具价值。(2)灰色关联分析法中关联度的计算一般采取加权平均值的方式，并未考虑各评价因子的权重影响，模糊层次分析法则可大致确定各个评价因子的权重，以此弥补灰色关联法的不足。

2.1 确定参考序列和比较序列

参考序列(水质评价标准)记为：Yi(k)={Yi(1)，Yi(2)， …，Yi(n)}，比较序列(水质样本)记为：Xj(k)={Xj(1)，Xj(2)， …，Xj(n)}。其中k表示评价因子(k=1，2，…，n)，i表示水质标准分级类别(i=1，2，…，5)，j表示水样采样点类别(j=1，2，…，m)。

2.2 无量纲化处理

无量纲化处理采用被量化值与各级标准值的平均值相比的方法进行[9]。水质标准矩阵和水质样本矩阵无量纲化处理后分别记为Uij(k)和Vij(k)，计算公式如下：

标准矩阵无量纲化计算公式为：

(3)

样本矩阵无量纲化计算公式为：

(4)

2.3 计算灰色关联系数

首先计算样本矩阵与标准矩阵差的绝对值Δij(k)：

Δij(k)=|Uij(k)-Vij(k)|。

(5)

式中：Δij(k)代表第j个采样点评价因子k对应的i类分级标准的绝对差值。

然后从中取最大差值Δmax，记为M；取最小差值Δmin，记为m。

则灰色关联系数的计算公式如下：

(6)

式中：ξij(k)为第j个水样采样点的评价因子k对应的i类分级标准的关联系数；ρ为分辨系数，取值范围为0到1。

2.4 计算灰色加权关联度

在模糊层次分析法确定的各评价因子权重的基础上，计算考虑各个评价因子间权重差异的灰色加权关联度。公式如下：

(7)

式中：Wk为模糊层次分析法确定的评价因子k的权重值；Zj为第j个水样采样点的评价因子k对应的i类分级标准的关联度。

根据计算得出的灰色加权关联度，以及最大关联度法则，关联度越大，则表明此采样点处的水质与该水质标准等级集合的关联程度越好，由此便可确定水质评价等级。

3 应用实例

3.1 评价因子的选择

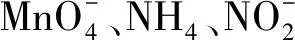
3.2 研究区评价因子权重计算

首先对本次参评的评价区的五类评价因子，采用两个或多个领域专家打分的方法分别对各因子进行两两比较判断，构建权重模糊互补判断矩阵A，如下：

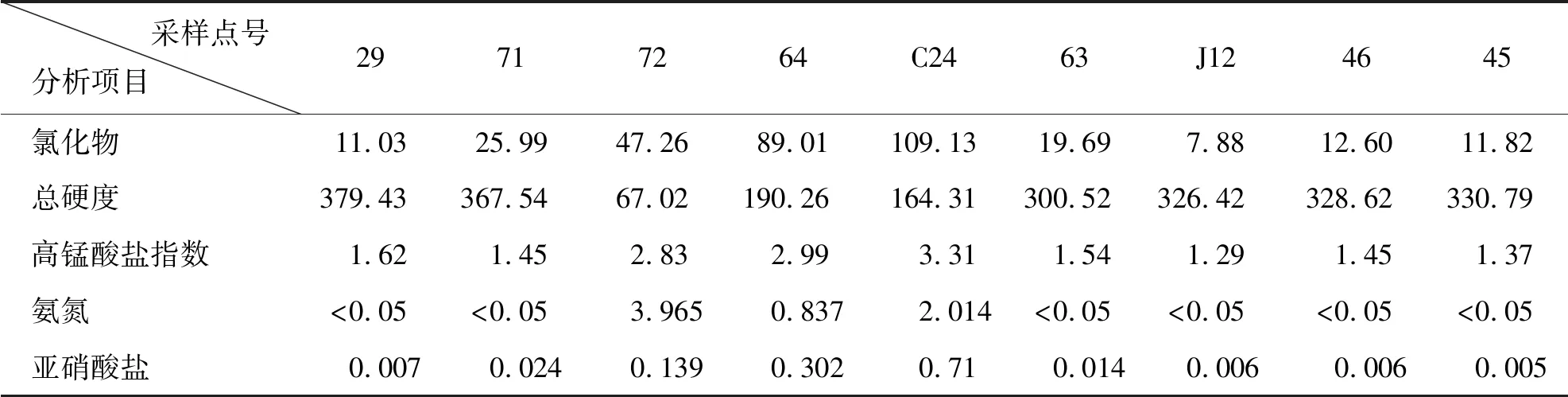
表2 水质监测值

表3 水质评价标准值

根据公式(1)，计算模糊一致性矩阵R如下：

根据公式(2)，计算各个参评因子的权重值，结果如下：

W=[0.150 0.150 0.150 0.275 0.275]。

3.3 利用评价方法计算水质等级

3.3.1对原始数据进行无量纲化处理

比较序列选取表2中的水质监测值，参考序列本应选取水质评价标准值(表3)，但会造成Ⅳ类、Ⅴ类评价标准数值的取值一致，因此本文对水质评价标准值进行一定的变换。以氯化物为例，其Ⅰ类到Ⅴ类评价标准数值为50、150、250、350、350。其中Ⅰ类水的区间为0～50，取其平均值作为Ⅰ类水质的参考值，即取25。则氯化物的Ⅰ类到Ⅴ类标准数值变换为25、100、200、300、350(Ⅴ类值不变换)。本次参考序列选取变换后的水质评价标准值，见表4。

以29号采样点为例，根据公式(3)、(4)对被量化值进行无量纲化处理，结果见表5。

表4 变换后的水质评价标准取值

表5 数值无量纲化处理

3.3.2关联系数计算

根据公式(5)计算差序列Δij(k)，结果如下：

其中k表示评价因子，i表示水质标准类别。

Δi1(k)中M=2.5690，m=0.0128。然后根据公式(6)计算灰色关联系数。需要注意的是ρ的取值，ρ的取值范围为[0，1]，一般当比较序列中出现异常值时，ρ应取较小的值，以消除异常值的支配作用[11]。水质评价领域中，将超过或远超过Ⅴ类水质标准值的评价因子的值视为异常值，且在水质评价中，往往需要突出而非消除异常值的作用，因此，ρ应取较大的值，本次计算中取ρ=0.9。灰色关联系数计算结果如下：

3.3.3灰色加权关联度计算

结合模糊层次分析法确定的各评价因子的权重，按照公式(7)进行加权关联度计算。

Z1= [0.150 0.150 0.150 0.275 0.275]×

=[0.9016 0.9325 0.8915 0.6597 0.5618]。

最大灰色加权关联度Z1max=0.9325，则该点号水质等级为Ⅱ级。同理，可以得出其他采样点的水质评价等级。通过此方法得出各采样点的水质评价结果见表6。

表6 基于模糊层次分析的灰色关联法得出各采样点的水质等级

3.4 比较分析

同时运用综合指数法对此例进行水质评价，确定水质评价级别，并将两种方法的评价结果进行比较，对产生的差异进行分析。比较结果见表7。

从表7可以发现两种方法的评价结果几乎一致，只有一个点的结果有差异，证明了基于模糊层次分析的灰色关联法在地下水水质评价中的可行性。以下对所产生的差异进行分析：

(1)综合指数法将各种污染物的污染指数纳入评价方法，同时加大了最严重污染物的污染指数的权重，使得评价结果表现为过度保护，导致水样水质等级划分偏高。可见表7中71号采样点采用综合指数法评价结果高于基于模糊层次分析的灰色关联法所得结果。

表7 两种方法得出的地下水质量评价结果

(2)基于模糊层次分析的灰色关联法弥补了灰色关联法采用加权平均值方式的不足，利用模糊层次分析法计算水质评价因子的权重，在此基础上利用灰色关联法计算关联度。此外，模糊层次分析法为偏于主观的评判方法，灰色关联法采用的是客观评判的方法。将两种方法进行结合，其评价结果更具价值。

4 结论

(1)将模糊层次分析法应用到地下水水质评价中，计算各评价因子的权重，既考虑了人为判断的模糊性，也省去了使用层次分析法计算权重时对判断矩阵的一致性检验。此外，模糊层次分析法计算的是考虑各个评价因子间权重差异的灰色关联度，弥补了以往使用灰色关联法时，使用加权平均值方式的不足，使得评价结果更具价值。

(2)地下水水质评价是多因素影响的复杂系统，因此引入灰色关联法，同时结合模糊层次分析法，建立基于模糊层次分析的灰色关联评价方法。充分考虑了评价方法的主观性与客观性，同时与综合指数法的评价结果进行比较，仅有一处采样点的评价结果存在差异，证明了这种方法的可行性，也为今后进行地下水水质评价提供了一定的借鉴及依据。

(3)采取基于模糊层次分析的灰色关联方法进行水质评价时，应注意以下几点：1)使用模糊层次分析法计算权重时，要全面分析研究区区域资料及现实情况，并充分考虑专家评审意见。2)考虑到水质评价中应适当突出污染因子(异常值)的作用，使用灰色关联法时应取较大的分辨系数值。