不同交通状态下直左交通冲突模型研究

王教文

(济南市公安局交警支队历下区大队，山东济南 250011)

0 引言

交通冲突是在可观测条件下，两辆或两辆以上车辆在同一时间、空间上相互接近，如果其中一方采取非正常交通行为，如转换方向、改变车速、突然停车等，除非另一方也相应采取避险行为，否则可能会发生碰撞，这一现象就是交通冲突[1]。交通事故是指车辆在道路上因过错或者意外造成人身伤亡或者财产损失的事件[2]。通常多使用交通事故数据来进行道路安全评价，然而，交通事故数据难以获取，随机性高，获取周期长，精度低，不能有效评价道路安全水平。考虑到交通冲突数据获取容易、数据集完整、成本低，交通事故与交通冲突关联性强、特征类似，可以通过交通冲突模型进行道路安全评价，分析交通流状态对交通冲突的影响[3]。

现有交通冲突模型主要侧重于简单回归模型的使用(包括泊松模型、负二项分布模型、正态分布模型等)[4-10]。Sayed等[11]采用线性回归模型分析无信号交叉口与信号交叉口的交通流量与交通冲突之间的关系，但是交通冲突数据离散且随机、非负，服从连续的正态分布，回归拟合时存在估计偏差。Sacchi等[12]对交通流量与追尾冲突进行研究，并建立泊松追尾冲突模型，分析交通流对追尾冲突的影响。Zhang等[13]应用负二项分布建立直左冲突模型，对交通流与直左冲突频率的影响进行研究。郭延永等[14-15]使用负二项分布建立右转交通冲突模型，综合分析影响右转设施的因素，并应用右转交通冲突模型指导交叉口右转渠化设置。

由于在不同交通状态下交通冲突的频率与车辆运行状态存在差异，使用简单的回归模型无法表征不同状态下发生交通冲突的关联性，模型拟合的精度低，交通冲突分析存在推断误差。马尔科夫链蒙特卡罗(markov chain monte carlo，MCMC)方法把未知变量看成随机变量，并使用概率分布描述变量，可以分析所有随机变量之间的相关性，适用于不同交通状态下交通冲突的研究。Jackman等[16]介绍MCMC方法，主要用于未知随机参数的估计，推动MCMC方法的发展。

本文根据信号交叉口车辆运行畅通情况、发生冲突的概率和单位时间内交通冲突数的差异划分不同的交通状态，在研究简单回归模型的基础上，基于MCMC方法，构建交通冲突独立状态下单维泊松对数正态贝叶斯组合回归(poisson logarithmic normal bayesian combination regression，PLCR)直左交通冲突模型和不同交通状态下的多维泊松对数正态贝叶斯组合回归(multidimensional poisson logarithmic normal bayesian combination regression，MPLCR)直左交通冲突模型，对不同交通状态下的直左交通冲突进行分析。

1 数据准备和冲突类型

利用山东省城市智能交通系统，选取山东省济南市直左冲突多发、几何设计特征相似的20个信号交叉口，并从智能交通系统中提取交叉口事故多发点的直左冲突事故数据和事故发生时间段内的交通流数据，通过数据的筛选和异常数据的剔除，获得20个交叉口视频检测器采集的200 h交通流量数据，提取到3000起直左冲突事故数据。

采用时间距离法选择碰撞时间(time to collision，TTC)为指标，计算不同冲突碰撞时间差tTTC，求出相应的交通冲突事故发生概率，并判别不同交通冲突发生的可能性[17]。设1车到达冲突点所用时间为t1，2车到达冲突点所用时间为t2，考虑位于碰撞轨迹上的两车保持某一时刻的路径和速度不变，计算1车和2车发生不同类型冲突的碰撞时间差

tTTC1=d1/v1-d2/v21, 正向冲突

(1)

tTTC2=(x2-x1)/(v1+v2), 对向冲突

(2)

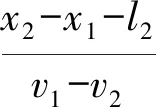
(3)

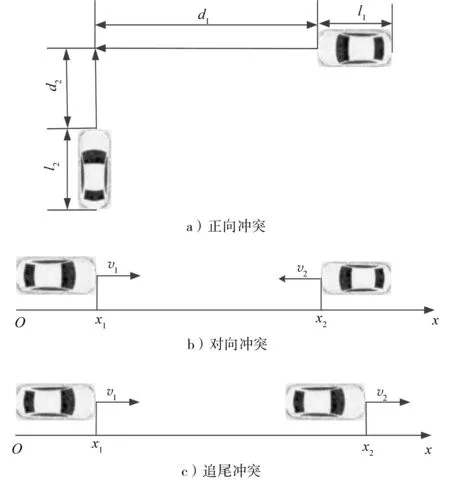
图1 两车3种交通冲突示意图

式中：d1、d2分别为1、2车某一时刻所处位置距冲突点的距离；v1、v2分别为1、2车的车速，x1、x2分别为1、2车某一时刻的初始位置坐标，l1、l2分别为1、2车的车长。3种交通冲突的示意图如图1所示。

tTTC越大，驾驶员的反应时间越充足，冲突事故发生的可能性越小；反之，tTTC越小，事故就越容易发生。因而，当tTTC=0时，可以认为事故一定发生。以tTTC为自变量，采用单调递减函数分析交通冲突与事故发生的关系[18]。则事故发生的概率

(4)

式中:a、b为模型参数，考虑到P∈[0,1]，可以取a=0，b=1；t0为驾驶员规避交通事故的反应时间，一般取t0=2.5 s。

2 不同交通状态的划分

交通冲突产生的实质是不同方向的车流为了占用同一道路，相互影响、相互作用的结果[19]。本文中研究的直左冲突可以理解为:拥有左转允许相位的对向进口左转车流为了抢占道路资源，与本应优先通行的直行穿越交叉口的车流发生碰撞或刮擦事故。

实际交通流量与道路基本通行能力之比，即q/c(q为实际交通流量，c为基本通行能力)反映交通流的状态，交通状态不同，直行车流与左转车流的相互影响结果不同,因此可以依据q/c划分交通状态。信号交叉口交通流i的实际交通流量qi可以通过城市信号控制系统直接提取。交通流的基本通行能力

ci=3600αgi/hiC，

(5)

式中：α为交通冲突影响系数，已知发生冲突的概率P以及单位时间内的交通冲突数和道路组织渠化，可参照文献[7]中交通冲突对道路通行能力影响系数的计算方法求出；gi为信号交叉口交通流i的相位绿灯时间；hi为信号交叉口交通流的饱和车头时距，可以通过城市数字系统提取；C为信号交叉口的周期时长。

根据收集的直左交通样本数据和对应的信号交叉口直行或左转的交通流数据,通过式(1)～(5)计算不同车流的qi/ci。根据计算结果，取直行qzx/czx=0.34和左转qzz/czz=0.25为分界值(其中qzx、czx分别为信号交叉口直行车流的实际交通流量与基本通行能力；qzz、czz分别为信号交叉口左转车流的实际交通流量与基本通行能力)，将交通状态划分为4种：

1)状态1。qzx/czx>0.34，qzz/czz>0.25；

2)状态2。qzx/czx≤0.34，qzz/czz≤0.25；

3)状态3。qzx/czx>0.34，qzz/czz≤0.25；

4)状态4。qzx/czx≤0.34，qzz/czz>0.25。

为了满足样本需求，选择15 min 作为计数单位时间(以下简称单位时间)，各交通状态的多个变量(直左冲突频率、直行车流量、左转车流量)的均值、最小值、最大值及标准差，如表1所示。

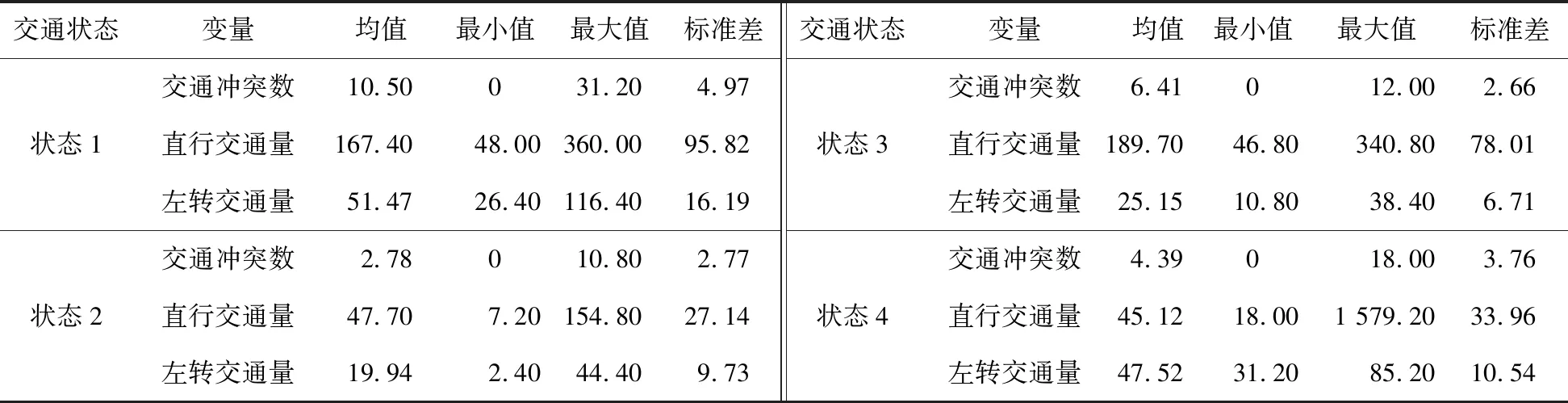
表1 不同交通状态变量的均值、最小值、最大值及标准差

由表1可以看出：不同交通状态下各变量的均值、最小值、最大值及标准差均存在差异，说明不同交通状态下的车辆运行情况不同，造成交通冲突发生的概率不同，从而引起交通冲突数的差异。

3 直左交通冲突模型构建

3.1 独立状态下PLCR直左交通冲突模型

一般来说，独立状态是指在建模过程中忽略不同交通状态对交通冲突的影响，将不同交通状态割裂开来，对交通冲突进行集计处理[20-21]。假设不同交通状态下交通冲突是相互独立的，忽略交通流之间的相关性。由于交通冲突数据非负、随机并且离散，采用传统的线性回归拟合方法，计算数据可能会产生偏估计。最基础的计数模型是泊松模型，本文在该模型的基础上推演出适应于独立状态下的PLCR直左交通冲突模型。

假设Yi(i=1,2,……，n)(n为样本总数)为单位时间内第i个样本的交通冲突数，各时间段i的交通冲突次数相互独立，可以采用同一泊松分布表示：

Yimi～Poisson(mi)，

式中mi为单位时间内第i个样本的期望冲突数。

通常将mi定义为影响冲突因素(如交通量、交通与几何设计特征)的函数，即

mi=μiexp(εi)，

式中：μi为引入误差项后单位时间内第i个观测样本的交通冲突数的期望值，μi=exp(β0)VTβ1VLβ2，其中VT为15 min内的直行交通量,VL为15 min内的左转交通量，β0、β1、β2为模型需要估计的参数；εi为第i个样本的交通冲突次数的误差项。

当exp(εi)误差项服从对数正态分布时，即

exp(εi)|Σ～Lognormal(0,Σ),

式中：Σ为误差项εi对数正态分布的方差。

则PLCR模型为：

Yiμi,Σ～PLCR(μi,Σ)，

PLCR模型的均值和方差

E(Yi)=μiexp(0.5,Σ)，

(6)

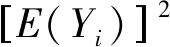
(7)

式中：E(Yi)为Yi的均值；D2(Yi)为Yi的方差。

3.2 不同交通状态下 MPLCR直左交通冲突模型

实际上，交通状态与交通冲突的发生存在密切联系，不同交通状态下，车辆运行情况不同，交通冲突发生的概率不同[22-23]。相邻的交通状态过渡时，车辆运行状态具有类似性，比如从饱和交通流到微饱和交通流时，车辆都是缓缓行驶，并非是从拥堵驾驶直接变为自由驾驶，所以相邻2个交通流状态之间，单位时间内交通冲突数并非完全独立，而是相互关联的[24-25]。因而在建模的过程中，需要分析不同的交通状态下直左冲突状况并建立相应的模型。考虑传统的线性回归模型可能会存在估计偏差，在泊松分布的基础上，建立可以分析不同交通状态下直左交通冲突差异和关联性的MPLCR直左交通冲突模型。

假设Yik服从参数为mik的泊松分布，可记为

Yik|mik～Poisson(mik)，

式中：Yik为单位时间内第i个样本在第k类交通状态下的交通冲突数，k=1，2，……，K，K为交通流状态总数;mik为第i个样本处于第k类交通流状态的交通冲突次数的期望值。

泊松模型一个很重要的前提假设是冲突频次的均值等于方差，为处理交通冲突数据的离散性、随机性，引入误差项εik，有：

ln(mik)=ln(μik)+εik,

式中：μik为引入误差项后第i个样本在第k类交通状态下交通冲突数的期望值，μik=exp(βk0)VTβk1VTβk2,其中：βk0、βk1、βk2为模型需要估计的参数；εik为第i个样本在第k类交通状态下的误差项。

当误差项εik服从均值为0、方差为∑′的多维正态分布时，得到MPLCR直左交通冲突模型

Yikμik,Σ′～MPLCR(μik,Σ′)，

则MPLCR模型的均值和方差

E(Yik)=μikexp(0.5,Σ′)，

(8)

D2(Yik)=E(Yik)+[E(Yik)]2(exp(Σ′)-1)，

(9)

式中：E(Yik)为Yik的均值；D2(Yik)为Yik的方差。

4 模型比较与结果分析

4.1 模型标定与精度比较

使用Winbugs软件对收集到的交通流数据和交通冲突数据进行处理，并采用文献[16]贝叶斯估计方法对模型中的待估计参数集β,Σ进行标定，其中PLCR模型在4种状态下Σ=[0.28 0.36 0.34 0.31],而MPLCR模型需要考虑不同状态的关联性，所以标定的Σ′为：

利用样本数据标定β，并分别计算出β的均值、标准差、90%置信区间分别如表2、3所示。

表2 MPLCR模型参数估计结果

表3 PLCR模型参数估计结果

由表2、3可知：MPLCR模型与PLCR模型不同交通状态下参数β标定的结果相似，两模型标定参数β的标准差离散程度低，90%置信区间包含所有总体标定参数且差异性小，适用于交通冲突分析，但是从整体的模型参数标定结果看，MPLCR模型优于PLCR模型，MPLCR模型的精度高于PLCR模型。

为进一步比较两模型的精度，根据文献[16]中贝叶斯预测的模型的精确度与期望方差成反比，因而可以采用两模型的期望方差比来表示模型的精度比。所以MPLCR和PLCR模型的精度比可表示为：

PrM/PrP=D2(YikM)/D2(YiP)。

(10)

已知引入误差项后交通冲突数的均值μi和误差项的标准差Σ，由式(6)～(9)可以分别求出MPLCR模型的期望方差D2(YikM)和PLCR模型的期望方差D2(YiP)，并由式(10)计算MPLCR模型和PLCR模型的精度比。通过计算可知，交通状态1、2、3、4的精度比分别为2.2、1.8、2.1、2.2，可以说明MPLCR模型比PLCR模型精度高2.2倍左右。

4.2 结果分析

利用Winbugs软件和matlab2016软件对MPLCR模型进行拟合，不同交通状态下各变量的均值如表4所示。

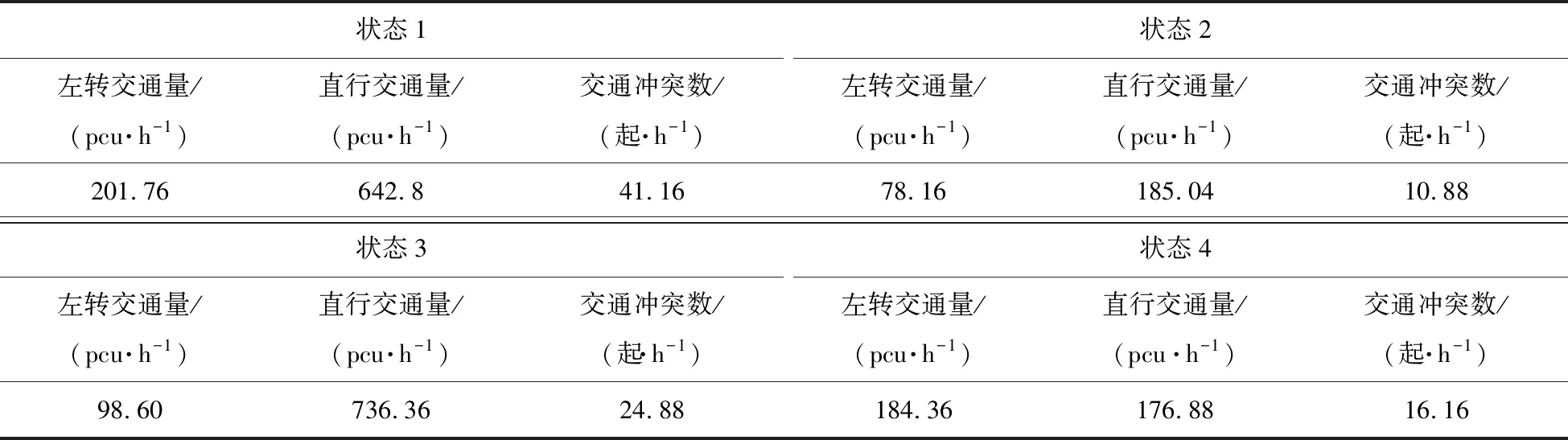
表4 不同状态下MPLCR模型各变量的拟合均值

由表4可以看出：

1)最大冲突次数出现在状态1中。此时对向直行交通流量和左转交通流量的均值都较高，左转车流难以从对向直行车流中寻找可插车间隙，左转车辆需要停留等待，以寻找可插车间隙通过交叉口。随着等待时间的增加，驾驶员的耐心减少，因此驾驶员愿意接受较小的可插车间隙而强行通过交叉口，导致对向直行车辆不得不采取减速或者刹车的避险行为，从而发生直左冲突。

2)最小冲突数出现在状态2中。此时对向直行交通流量和左转交通流量的均值都相对较小。由于对向直行车流通常是成组到达，因而左转车流很容易从各组对向直行车流中寻找可插车间隙，继而快速通过交叉口，所以单位时间内发生交通冲突的概率较小。

3)状态3中左转车流对冲突产生的影响大于直行流量。此状态中直行交通流量的均值相对较大，即直行车流量较大，所以对向直行车流的可穿越间隙比较稳定，在该状态下增加左转交通量更容易产生交通冲突。

4)状态4中直行车流量对冲突产生的影响大于左转车流量。此时左转交通流量的均值相对较大，即左转交通流量较大，当増加直行交通流量时，导致直行车流的可穿越间隙减少，所以该状态下增加直行交通量更容易产生交通冲突。

分析得到：若保持左转车流量不变，当直行车流量増加1%时，交通状态1～4的直左冲突次数分别增加0.48%、0.54%、0.29%和0.82%；当保持直行交通流量不变时，左转交通流量増加1%时，交通状态1～4的直左冲突频次分别增加0.46%、0.78%、0.48%和0.56%。说明在不同交通状态中，同一股冲突交通流的作用效果不同。

4 结论

在不同交通状态下，信号控制交叉口的直左交通冲突相互关联。独立状态下单维泊松对数正态贝叶斯组合回归直左冲突模型，无法量化分析不同交通状态下交通流与交通冲突之间的相互作用关系，其模型精度远低于多维泊松对数正态贝叶斯组合回归直左冲突模型。而多维泊松对数正态贝叶斯组合回归直左冲突模型，可以通过控制直行交通流或左转交通流保持不变，定量分析不同状态下交通流与交通冲突的影响。此外，利用交通冲突技术建立冲突模型，有别于传统冲突模型，为其他交通冲突模型的研究提供了新思路。